洛谷 P1219 [USACO1.5] 八皇后 Checker Challenge-普及/提高-

题目描述

一个如下的 $6\times 6$ 的跳棋棋盘，有六个棋子被放置在棋盘上，使得每行、每列有且只有一个，每条对角线（包括两条主对角线的所有平行线）上至多有一个棋子。

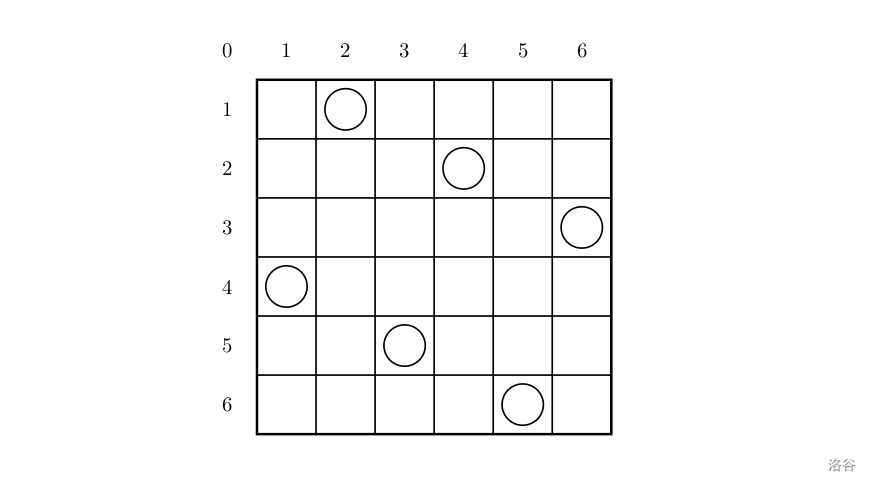
上面的布局可以用序列 $246135$ 来描述，第 $i$ 个数字表示在第 $i$ 行的相应位置有一个棋子，如下：

行号 $123456$

列号 $246135$

这只是棋子放置的一个解。请编一个程序找出所有棋子放置的解。
并把它们以上面的序列方法输出，解按字典顺序排列。
请输出前 $3$ 个解。最后一行是解的总个数。

输入格式

一行一个正整数 $n$，表示棋盘是 $n\times n$ 大小的。

输出格式

前三行为前三个解，每个解的两个数字之间用一个空格隔开。第四行只有一个数字，表示解的总数。

输入输出样例 #1

输入 #1

6

输出 #1

2 4 6 1 3 5
3 6 2 5 1 4
4 1 5 2 6 3
4

说明/提示

【数据范围】
对于 $100\%$ 的数据，$6\le n\le 13$。

题目翻译来自NOCOW。

USACO Training Section 1.5

solution

题目大意

在一个 n x n (n <= 13) 的网格里放置 n 个棋子（皇后），要求它们不能同行、同列、同斜线，求可能的方法数量。

思路

直接从逐行尝试，只要是和之前放置的不冲突就一直放到最后，有冲突就换一条路继续尝试，直到所有的方式都尝试过即可，所以本质就是穷举法。这种方法叫做回溯法，因为就是不断试错，不断回溯，不适合大数据范围。

即使数据量很小，但 n = 13 时仍然超时，所以可以进行改进。
将检查冲突的部分，直接用数组记录下来，记录每一行、每一列、每条左斜线、每条有些线是否放置了皇后，而不用去搜索。

代码

#include <sstream>
#include "iostream"
#include "math.h"
#include "algorithm"
#include "string.h"
#include "unordered_set"
#include "deque"
#include "stack"
#include "queue"
#include "vector"
#include "unordered_map"

using namespace std;
int n;

int a[14]; // a[i]:第 i 行的皇后放的位置
int s = 0;

bool is_ok(int i, int k) { // 检查冲突
    for (int j = 1; j < i; j++) {
        if (a[j] == k || i - j == abs(k - a[j]))
            return false;
    }
    return true;
}

void f(int i) { // dfs 深度搜索
    if (i > n) {
        if(s < 3) {
            for (int k = 1; k <= n; k++) {
                cout << a[k] << " ";
            }
            cout << endl;
        }
        s++;
        return;
    }

    for (int k = 1; k <= n; k++) {
        if (is_ok(i, k)) {
            a[i] = k;
            f(i + 1);
        }
    }
}


int main() {
    cin >> n;
    f(1);
    cout << s;
    return 0;
}

结果

即使数据量很小，但 n = 13 时仍然超时，所以可以进行改进。
将检查冲突的部分，直接用数组记录下来，记录每一行、每一列、每条左斜线、每条有些线是否放置了皇后，而不用去搜索。

代码

#include <sstream>
#include "iostream"
#include "math.h"
#include "algorithm"
#include "string.h"
#include "unordered_set"
#include "deque"
#include "stack"
#include "queue"
#include "vector"
#include "unordered_map"
#include "time.h"

using namespace std;
int n;

int a[14]; // 存放的位置
int b[14]; // 记录该列有没有存数
int c[30]; // 记录该对角线有没有存放数字
int d[30]; // 记录该对角线有没有存放数字

int s = 0;

void f(int i) {
    if (i > n) {
        if (s < 3) {
            for (int k = 1; k <= n; k++) {
                cout << a[k] << " ";
            }
            cout << endl;
        }
        s++;
        return;
    }

    for (int k = 1; k <= n; k++) {
        if (b[k] == 0 && c[i + k] == 0 && d[n - i + k] == 0) {
            a[i] = k;
            b[k] = 1, c[i + k] = 1, d[n - i + k] = 1;
            f(i + 1);
            b[k] = 0, c[i + k] = 0, d[n - i + k] = 0;
        }
    }
}


int main() {
    cin >> n;
    f(1);
    cout << s;
    return 0;
}

结果