1 题目:岛屿数量
官方标定难度:中
给你一个由 ‘1’(陆地)和 ‘0’(水)组成的的二维网格,请你计算网格中岛屿的数量。
岛屿总是被水包围,并且每座岛屿只能由水平方向和/或竖直方向上相邻的陆地连接形成。
此外,你可以假设该网格的四条边均被水包围。
示例 1:
输入:grid = [
[“1”,“1”,“1”,“1”,“0”],
[“1”,“1”,“0”,“1”,“0”],
[“1”,“1”,“0”,“0”,“0”],
[“0”,“0”,“0”,“0”,“0”]
]
输出:1
示例 2:
输入:grid = [
[“1”,“1”,“0”,“0”,“0”],
[“1”,“1”,“0”,“0”,“0”],
[“0”,“0”,“1”,“0”,“0”],
[“0”,“0”,“0”,“1”,“1”]
]
输出:3
提示:
m == grid.length
n == grid[i].length
1 <= m, n <= 300
grid[i][j] 的值为 ‘0’ 或 ‘1’
2 solution
可以采用深度优先遍历,访问未访问过的陆地,并递归访问四周的陆地。
代码
class Solution {
public:
void find(int r, int c, int *dr, int *dc, vector<vector<bool>> &vis, vector<vector<char>> &grid) {
if (vis[r][c]) return;
vis[r][c] = 1;
for (int i = 0; i < 4; i++) {
int rr = r + dr[i];
int cc = c + dc[i];
if (rr >= 0 && rr < grid.size() && cc >= 0 && cc < grid[0].size() && grid[rr][cc] == '1') {
find(rr, cc, dr, dc, vis, grid);
}
}
}
int numIslands(vector<vector<char>> &grid) {
int dr[] = {1, 0, -1, 0};
int dc[] = {0, 1, 0, -1};
int m = grid.size();
int n = grid[0].size();
vector<vector<bool>> vis(m, vector<bool>(n, 0));
int cnt = 0;
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
if (!vis[i][j] && grid[i][j] == '1') {
find(i, j, dr, dc, vis, grid);
cnt++;
}
}
}
return cnt;
}
};
结果
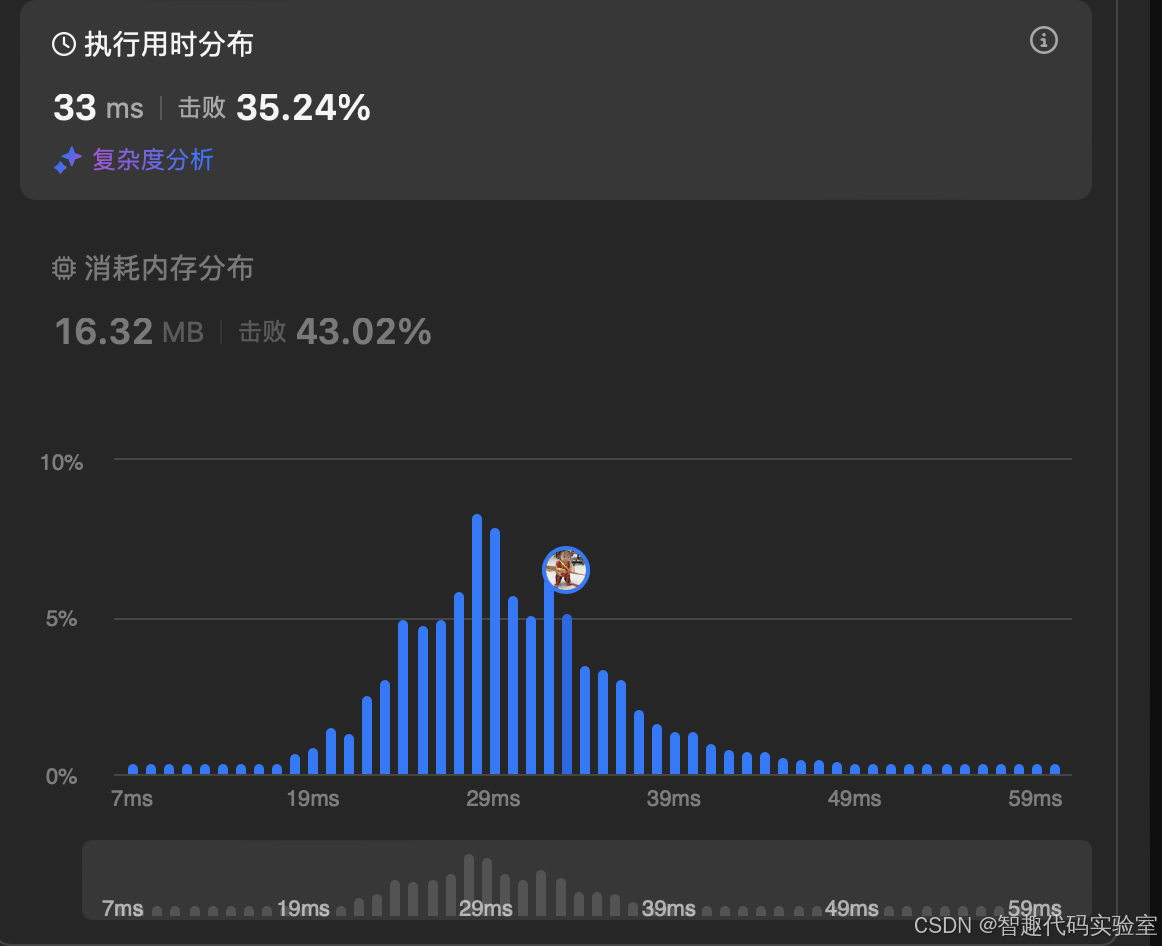






















 570
570

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










