汇总:
Chamfer距离(Chamfer Distance)和Fréchet距离(Fréchet Distance)是两种常用于评估曲线或多线段相似性的度量方法
1 Chamfer距离:两个无序点集之间相似性
定义:Chamfer距离用于量化两个无序点集之间的相似性。
其计算公式为:
1.1.1 特点:
- 仅考虑点之间的最近邻距离,忽略点的顺序。
- 适用于无序点集(如点云、多线段顶点集)的相似性比较。
- 计算效率较高,常用于3D重建、点云生成等任务中作为损失函数。
2 Fréchet距离
定义:Fréchet距离同时考虑曲线的空间位置和点的顺序。其离散版本定义为:
2.1.1 特点:
- 需要保证曲线的顺序一致性(如轨迹、多线段的顶点顺序)。
- 直观理解为“遛狗问题”:主人和狗沿两条路径行走时所需的最短狗绳长度。
- 计算复杂度较高,通常用于需要严格对齐顺序的场景(如地图匹配、自动驾驶中的车道线检测)。
2.1.2 输出:
Fréchet距离输出的是两条曲线的最优匹配下的最大局部距离,核心是寻找两条曲线在所有可能匹配方式中最大局部距离的最小值(即“最短狗绳长度”)
- “最大局部距离”:
在两条曲线的匹配过程中,每一步的匹配点对 (pi,qj)都有一个距离 d(pi,qj),所有匹配点对中的最大距离即为当前匹配方案的“最大局部距离”。- “最小值”:通过调整匹配顺序(即参数化函数 α\alphaα 和 β\betaβ),寻找所有可能的匹配方案中最小的那个“最大局部距离”。
Chamfer Distance 是一种用于衡量两个点云之间相似度的度量方法。它的定义如下:给定两个点云 P 和 Q,Chamfer Distance 是 P 中每个点到 Q 中最近的点的距离的平方和与 Q 中每个点到 P 中最近的点的距离的平方和的平均值。简言之,Chamfer Distance 是一种衡量两个点云之间距离的度量方法。
计算 Chamfer Distance 需要先确定每个点在另一个点云中的最近点。常用的算法有暴力匹配和 KD-Tree 匹配。暴力匹配的时间复杂度较高,而 KD-Tree 匹配可以在 O(n log n) 的时间复杂度内完成。在实际应用中,可以根据具体需求选择合适的算法。
Chamfer Distance 的应用场景非常广泛。例如,在机器人导航中,可以使用 Chamfer Distance 来比较地图和实际环境的差异,从而指导机器人正确地导航。在自动驾驶领域,Chamfer Distance 可以用于比较车辆周围环境的点云数据,以实现车辆的精确控制和避障。此外,Chamfer Distance 还广泛应用于场景重建、物体识别和三维模型匹配等领域。
为了更好地应用 Chamfer Distance,需要注意以下几点:
标准化点云数据:在进行 Chamfer Distance 计算之前,需要将点云数据进行标准化处理,使得每个点的坐标都在同一尺度上。这有助于提高计算的准确性和稳定性。
选择合适的算法:根据实际需求选择合适的算法来计算 Chamfer Distance。例如,对于大规模点云数据,可以选择 KD-Tree 匹配算法以提高计算效率;对于小规模点云数据,可以选择暴力匹配算法以获得更精确的结果。
参数调整:在应用 Chamfer Distance 时,需要根据实际情况调整相关参数。例如,在计算最近点时,可以根据实际情况调整距离阈值,以获得更准确的结果。
数据预处理:在进行 Chamfer Distance 计算之前,需要对点云数据进行预处理。例如,去除噪声、过滤异常值等,以提高计算的准确性和稳定性。
结果解读:在得到 Chamfer Distance 的结果后,需要根据实际需求解读结果的意义。例如,如果 Chamfer Distance 的值较小,说明两个点云相似度较高;如果值较大,则说明两个点云相似度较低。
总结起来,Chamfer Distance 是一种用于衡量两个点云之间相似度的度量方法。它广泛应用于场景重建、机器人导航、自动驾驶等领域。为了更好地应用 Chamfer Distance,需要注意标准化点云数据、选择合适的算法、调整参数、数据预处理和结果解读等方面。








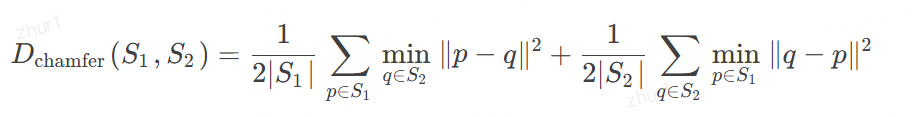
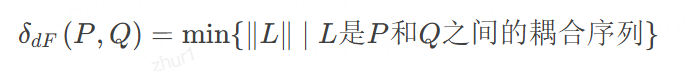
















 88
88

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








