黑白染色——封锁阳光大学

所谓黑白染色，就是指用bfs或dfs依次遍历每一个点，同时进行染色，一黑一白，如果遇到已经染过色的点并且点的颜色和即将要染的颜色冲突，就说明无法进行二分，无法满足染色。大概就是这样的。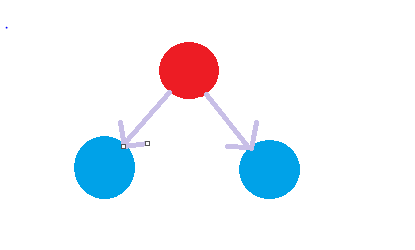

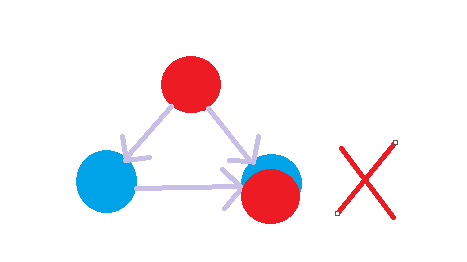
下面我们看一道例题：

 P1330 封锁阳光大学

题目描述

曹是一只爱刷街的老曹，暑假期间，他每天都欢快地在阳光大学的校园里刷街。河蟹看到欢快的曹，感到不爽。河蟹决定封锁阳光大学，不让曹刷街。

阳光大学的校园是一张由N个点构成的无向图，N个点之间由M条道路连接。每只河蟹可以对一个点进行封锁，当某个点被封锁后，与这个点相连的道路就被封锁了，曹就无法在与这些道路上刷街了。非常悲剧的一点是，河蟹是一种不和谐的生物，当两只河蟹封锁了相邻的两个点时，他们会发生冲突。

询问：最少需要多少只河蟹，可以封锁所有道路并且不发生冲突。

输入输出格式

输入格式：

 

第一行：两个整数N，M

接下来M行：每行两个整数A，B，表示点A到点B之间有道路相连。

 

输出格式：

 

仅一行：如果河蟹无法封锁所有道路，则输出“Impossible”，否则输出一个整数，表示最少需要多少只河蟹。

 

输入输出样例

输入样例#1： 

3 3
1 2
1 3
2 3

输出样例#1： 

Impossible

输入样例#2： 

3 2
1 2
2 3

输出样例#2： 

1

说明

【数据规模】

1<=N<=10000，1<=M<=100000，任意两点之间最多有一条道路。

 

很显然，这是一道裸的黑白染色题目，当然；也有别的解法，但我们这里学的是黑白染色，所以就用黑白染色写吧。

dfs遍历并染色，有冲突，输出impossible

                          没有冲突，就取黑点个数和白点个数的min

代码如下：

#include<iostream>
#include<cstdio>
#include<cstring>
#include<string>
#include<algorithm>
#define maxm 100000+5
#define maxn 10000+5

using namespace std;

int vis[maxn];
int n,m,head[maxn],v1=0,v2=0;
struct edge{
    int to,next,u;
}e[3*maxm];
int v[5];

int tot=0;
void add(int u,int v)
{
    e[++tot].to =v;
    e[tot].next=head[u];
    head[u]=tot;
}

void dfs(int u,int col)
{
    vis[u]=col;v[col]++;
    for(int i=head[u];i;i=e[i].next)
    {
        int to=e[i].to;
        if(!vis[to]) dfs(to,3-col);
        else if(vis[to]==col){
            printf("Impossible");
            exit(0);
           //正常退出
    
        }
    }
    
}

int x,y;

int main()
{
    
    scanf("%d%d",&n,&m);
    for(int i=1;i<=m;i++)
    {
        scanf("%d%d",&x,&y);
        add(x,y);
        add(y,x);
    }
    int ans=0;
    for(int i=1;i<=n;i++)
    {
        if(!vis[i]){
            v[1]=v[2]=0;
            dfs(i,1);
            ans+=min(v[1],v[2]);
        }
    }
    //printf("%d%d\n",v[1],v[2]);
    printf("%d",ans);
    
    return 0;
}    

如有错误，希望指出。

转载于:https://www.cnblogs.com/ZDHYXZ/p/8643327.html