HDU 1695 GCD

题目链接：http://acm.hdu.edu.cn/showproblem.php?pid=1695

题意:在[1,B]中取一个数x，在[1,D]中取一个数y，使得Gcd(x,y)=k?求这样的(x,y)有多少对?(5,7)和(7,5)算作一样的。

思路：首先B=B/k,D=D/k，这时就是Gcd(x,y)=1就行，就是互质。

 

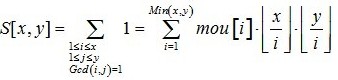
int mou[N];

void init()
{
    i64 i,j;
    for(i=2;i<N;i++) if(!mou[i])
    {
        mou[i]=i;
        for(j=i*i;j<N;j+=i) mou[j]=i;
    }
    mou[1]=1;
    for(i=2;i<N;i++) 
    {
        if(i/mou[i]%mou[i]==0) mou[i]=0;
        else mou[i]=-mou[i/mou[i]];
    }
    for(i=1;i<N;i++) mou[i]+=mou[i-1];
}

int a,b,c,d,K;

i64 cal(i64 n,i64 m)
{
    if(n>m) swap(n,m);
    i64 ans=0,L,R;
    for(L=1;L<=n;L=R+1)
    {
        R=min(n/(n/L),m/(m/L));
        ans+=(mou[R]-mou[L-1])*(n/L)*(m/L);
    }
    return ans;
}


int main()
{
    init();
    int num=0;
    rush()
    {
        RD(a,b); RD(c,d); RD(K);
        printf("Case %d: ",++num);
        if(K==0)
        {
            puts("0");
            continue;
        }
        b/=K; d/=K;
        if(b>d) swap(b,d);
        i64 ans=cal(b,d);
        i64 temp=cal(b,b);
        ans=ans-(temp-1)/2;
        PR(ans);
    }
    return 0;
}