幂级数和函数经典例题_三、复变函数的级数

1.复数项级数

复数列的极限，与高数中的基本一致，其收敛的充分必要条件便是实部虚部这两个实数收敛。

将复数列的前

项相加得其和

，当

时，便构成了一个复数项级数，与实数项级数相同，它也具有敛散性，其收敛的充分必要条件为实部虚部两个实数项级数都收敛。

高数中关于级数的一些有趣的推论或性质也可以推广到这里：

级数收敛，则其通项的极限为零
存在绝对收敛的概念，即由通项的模所构成的级数收敛的话，则称该级数绝对收敛
若一级数绝对收敛，则一定是收敛级数
收敛级数必有界

还有一个有趣的性质：

2.幂级数

将上述的通项

换为复变函数

,便可得到一个

复变函数项级数，即：

若在一点

处，级数

收敛，则称该函数项级数在

处收敛；若在

内的每一点都收敛，则该函数级数在区域

内收敛，并可求其

和函数：

情况再特殊一点，当 通项

为幂函数

,该级数便为

幂级数。接下来边讨论其敛散性。

首先给出Abel定理：

可以看出，与高数中的实数幂级数基本一致，所以这里也存在收敛半径的概念。高数中的收敛区间对应实数轴上的一段，而这里对应的是复平面上的圆域。

接下来便是求取幂级数的收敛半径，设一级数为

,为了用到正项级数中的比值法或根值法：

记

,则

根据比值法或根植法，

时，级数收敛，解除该不等式即可。边界值要单独讨论。

举个栗子：求解级数

的收敛半径。

，令其小于1，得

，故收敛半径为1，现在判断边界值是否成立，当

时，原级数变为

都收敛，故该级数在收敛圆周上也收敛。

这里的幂级数的性质和高数中的也类似，包括以下的有理运算性质

和下面的逐项求导和逐项积分性：

简单解释下逐项求导和逐项积分性：就是在收敛域内，级数有和函数

，该和函数的导数，等同于将级数逐项求导后的和（实际上就是个求导的性质）；该和函数的积分，等同于将级数逐项积分后的和 。

3.Taylor级数

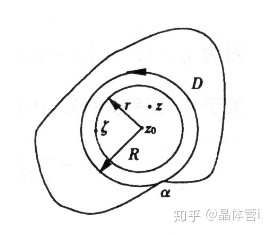
幂级数在收敛圆域内一定收敛到解析函数，同样的解析函数在解析点的某个邻域内一定可以展开成幂级数（不予证明），这就是Taylor级数。下面是系统的表达：

这实际上也给出了一种求Taylor级数收敛半径的方法：如下图，那个大圆是

的最大邻域，点

（在边界上）是距离

最近的不解析点（奇点），则

另外，Taylor展开是唯一的，就是说通项系数

唯一。

所以我们可以用一些间接方法求这个

：借助于一些已知的函数的展开式，结合一些性质（如；逐项积分、逐项求导）和代换等一些数学技巧，便可求出Taylor展开式而避免了复杂的求导。下面是几道例题。

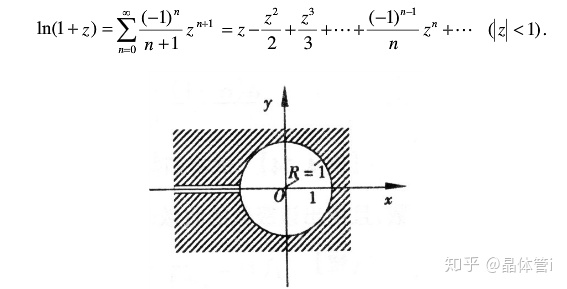
稍微提一嘴例4中为什么收敛半径是1，因为

在实轴上-1点左侧的区域无定义，故

的最大解析邻域为

的圆，也就是说，离

最近的奇点为

（-1，0），故

。其实最想说的一点就是，展开时不要忘了收敛半径这一条件。

4.Laurent级数

上面提到的Taylor级数是在

的某邻域圆内展开的，但如果要想在

这个圆环域内展开，因为那个小圆内可能有奇点，所以不一定能展开成

的幂级数，但可以展开为

的负指数次幂项的级数，这便为Laurent级数。

形式为：

该级数的收敛条件为

和

同时收敛。

接下来主要讨论负幂项部分

。设

则负幂项部分变为

，由上述的Taylor级数可知，

存在一个收敛半径

使其在内部收敛，也就是说

时负幂项部分收敛，收敛域为一个圆的外部。

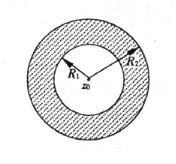
又因为

的收敛域为圆的内部

，故只有当

的时候，该Laurent级数才有一个收敛域

，这是一个圆环域。

类比Taylor级数，某函数在某定点的邻域圆内解析时，该函数可以展开为Taylor级数。那么在定点的某邻域圆环内是否可以展成Laurent级数呢？

答案当然是肯定的咯！如下便是Laurent展开定理：

根据Cauchy导数公式，如果

在

的内部都解析，则

。可以看出Laurent展开和Taylor展开的系数实质上是等价的，只不过Laurent展开时，无法确定

时

是否解析，故用积分形式表达

。当然，Laurent也具有唯一性。

Laurent展开时，因其中的

不好求得，常用间接方法计算。如下面例题：

有两个奇点：1和2。除此之外的所有点都解析，故题目中的四个小问题都是在

的解析域内，故都可展开

实际上（1）在

Laurent展开时，就相当于Taylor展开（

,最近的奇点

，所以

）。故Taylor展开可以看成Laurent展开的一种特殊形式，这时大圆

内部无奇点。

（2）中展开域变为

时，但

只有在

时才能展开，在（2）的条件中不能直接展开，但我们想到此时

，

可以展开，所以就将

化为

进行展开。第（3）问同样。

前三问都是在

处展开，但第（4）问是在

处展开，可以进行变量替换令

来进行计算。

PS：打公式太麻烦了，所以图片粘贴较多，请谅解，但所有的解释性语言均是手码出来的。有问题可以一起探讨~