cartographer代码学习笔记-CeresScanMatcher2D

Running小学生

于 2024-02-23 11:02:18 发布

阅读量351

点赞数

分类专栏： cartographer 文章标签：学习笔记

原文链接：https://www.cswamp.com/post/121

版权

cartographer 专栏收录该内容

20 篇文章

订阅专栏

转载https://www.cswamp.com/post/121
Ceres扫描匹配器优化包含了三个残差项：点云与grid的匹配残差、位置(平移)残差、角度(旋转)残差。位置、角度两残差顶多就是对匹配位姿的约束，防止点云匹配的结果和初值差太多，真正的扫描匹配的主角是点云匹配残差。

1、CeresScanMatcher2D::Match

Match执行ceres扫描匹配，CeresScanMatcher2D其它成员都是它的辅助函数。

void CeresScanMatcher2D::Match(const Eigen::Vector2d& target_translation,
                               const transform::Rigid2d& initial_pose_estimate,
                               const sensor::PointCloud& point_cloud,
                               const Grid2D& grid,
                               transform::Rigid2d* const pose_estimate,
                               ceres::Solver::Summary* const summary) const {

target_translation：odom坐标系下欲优化的local_pose中的平移部分。不受是否使用相关性扫描影响。
initial_pose_estimate：来自odom坐标系下欲优化local_pose。如果没使用相关性扫描，值就是local_pose，否则是相关性扫描找出的位姿。
grid：概率图。
point_cloud：经过重力修正后机器人(base_footprint)坐标系下的点云。就是LocalTrajectoryBuilder2D中的filtered_gravity_aligned_point_cloud。

  double ceres_pose_estimate[3] = {initial_pose_estimate.translation().x(),
                                   initial_pose_estimate.translation().y(),
                                   initial_pose_estimate.rotation().angle()};
  ceres::Problem problem;
  CHECK_GT(options_.occupied_space_weight(), 0.);
  switch (grid.GetGridType()) {
    case GridType::PROBABILITY_GRID:
      problem.AddResidualBlock(
          CreateOccupiedSpaceCostFunction2D(
              options_.occupied_space_weight() /
                  std::sqrt(static_cast(point_cloud.size())),
              point_cloud, grid),
          nullptr /* loss function */, ceres_pose_estimate);

点云匹配残差块。栅格图类型默认使用概率图，launcher用的也是概率图

      break;
    case GridType::TSDF:
      problem.AddResidualBlock(
          CreateTSDFMatchCostFunction2D(
              options_.occupied_space_weight() /
                  std::sqrt(static_cast(point_cloud.size())),
              point_cloud, static_cast(grid)),
          nullptr /* loss function */, ceres_pose_estimate);
      break;
  }
  CHECK_GT(options_.translation_weight(), 0.);
  problem.AddResidualBlock(
      TranslationDeltaCostFunctor2D::CreateAutoDiffCostFunction(
          options_.translation_weight(), target_translation),
      nullptr /* loss function */, ceres_pose_estimate);

平移残差块。

  CHECK_GT(options_.rotation_weight(), 0.);
  problem.AddResidualBlock(
      RotationDeltaCostFunctor2D::CreateAutoDiffCostFunction(
          options_.rotation_weight(), ceres_pose_estimate[2]),
      nullptr /* loss function */, ceres_pose_estimate);

旋转残差块。

  ceres::Solve(ceres_solver_options_, &problem, summary);

  *pose_estimate = transform::Rigid2d(
      {ceres_pose_estimate[0], ceres_pose_estimate[1]}, ceres_pose_estimate[2]);
}

CSM2D优化包含了三个残差：点云与grid的匹配残差、位置(平移)残差、角度(旋转)残差。其中，每种残差都有一个权重配置参数。

对于优化结果添加位置偏差量和角度偏差量的限定，我个人理解，通过位姿外推器算出的位姿基本上就在真值附近，如果优化后的结果出现了较大的偏差说明位姿跟丢了。位置、角度两残差项顶多就是对匹配位姿的约束，防止点云匹配的结果和初值差太多，真正的扫描匹配的主角是点云匹配残差，即OccupiedSpaceCostFunction2D。

2、点云匹配残差块：OccupiedSpaceCostFunction2D

点云匹配的目的就是在地图中找到一个位姿估计，使得在该位姿下所有hit点在grid(概率图)中的占据概率之和最大。记H={h_1，. . . h_k，. . .h_K}感器扫描到的K个hit点集合，h_k是第k个hit点在机器人坐标系(base_footprint)下的位置坐标。那么h_k在odom坐标系下的坐标可以表示为：

在这里插入图片描述

其中，在这里插入图片描述表示位姿估计，、分别是机器人在odom坐标系下的坐标，是机器人的方向角。用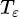表示位姿估计描述的坐标变换。我们根据hit点在odom坐标系下的位置坐标查找对应的占据概率，但由于栅格坐标相对来说是一个比较稀疏离散的采样，所以Cartographer在它的基础上进行了一次双三次(bicubic)插值在这里插入图片描述。因此优化的目标就是：
公式3：

2.1 CreateOccupiedSpaceCostFunction2D

ceres::CostFunction* CreateOccupiedSpaceCostFunction2D(
    const double scaling_factor, const sensor::PointCloud& point_cloud,
    const Grid2D& grid) {
  return new ceres::AutoDiffCostFunction<OccupiedSpaceCostFunction2D,
                                         ceres::DYNAMIC /* residuals */,
                                         3 /* pose variables */>(
      new OccupiedSpaceCostFunction2D(scaling_factor, point_cloud, grid),
      point_cloud.size());
}

class OccupiedSpaceCostFunction2D {
 public:
  OccupiedSpaceCostFunction2D(const double scaling_factor,
                              const sensor::PointCloud& point_cloud,
                              const Grid2D& grid)
      : scaling_factor_(scaling_factor),
        point_cloud_(point_cloud),
        grid_(grid) {}

  template <typename T>
  bool operator()(const T* const pose, T* residual) const {
    Eigen::Matrix<T, 2, 1> translation(pose[0], pose[1]);
    Eigen::Rotation2D<T> rotation(pose[2]);
    Eigen::Matrix<T, 2, 2> rotation_matrix = rotation.toRotationMatrix();
    Eigen::Matrix<T, 3, 3> transform;
    transform << rotation_matrix, translation, T(0.), T(0.), T(1.);

在函数的一开始，先把迭代的输入参数pose转换为坐标变换，存储在临时变量transform。然后使用Ceres库原生提供的双三次插值迭代器。

    const GridArrayAdapter adapter(grid_);
    ceres::BiCubicInterpolator<GridArrayAdapter> interpolator(adapter);
    const MapLimits& limits = grid_.limits();

    for (size_t i = 0; i < point_cloud_.size(); ++i) {
      // Note that this is a 2D point. The third component is a scaling factor.
      const Eigen::Matrix<T, 3, 1> point((T(point_cloud_[i].position.x())),
                                         (T(point_cloud_[i].position.y())),
                                         T(1.));
      const Eigen::Matrix<T, 3, 1> world = transform * point;
      interpolator.Evaluate(
          (limits.max().x() - world[0]) / limits.resolution() - 0.5 +
              static_cast<double>(kPadding),
          (limits.max().y() - world[1]) / limits.resolution() - 0.5 +
              static_cast<double>(kPadding),
          &residual[i]);
      residual[i] = scaling_factor_ * residual[i];

根据公式(3)针对每个hit点计算对应的残差代价。在“transform * point”，通过hit点坐标(base_footprint坐标系)与transform的相乘得到其在odom坐标系下的坐标。
interpolator.Evaluate行则通过刚刚构建的迭代器和hit点在odom坐标系的米格式坐标world，获取在hit点是占据的概率。该函数调用有三个参数，前两个参数用来描述world点在概率图的index格式坐标，第三个参数用于记录插值后的结果。计算时是通过GridArrayAdapter类中成员函数GetValue获取附近几个栅格数据，然后求它们双三次插值后的值。此外由于栅格中原本存储的就是栅格空闲的概率，所以这里查询出来的概率就是在这里插入图片描述。
residual[i]是何值？——举个例子，point_cloud_[i]点的坐标不在概率图内（实际不可能发生，这里只为说residual[i]值），而且BiCubicInterpolator在计算“均值”时，邻近点的坐标也不在概率图内，根据GridArrayAdapter::GetValue行为，不在概率图内的都返回kMaxCorrespondenceCost(0.9)。那BiCubicInterpolator计算出的“均值”也会是0.9，进而由此得到的residula[i]值也是0.9。residual[i]表示的是在point_cloud_[i]这个栅格上空闲概率。

如何求world点在概率图的Index格式坐标？——MapLimits::GetCellIndex(const Eigen::Vector2f& point)用于把某个米格式坐标转换成Index格式坐标，内中像计算x的方法是common::RoundToInt((max_.x() - point.x()) / resolution_ - 0.5)。这里计算方法类似那里，只是改了两点。1）因为双三次插值须要Index是浮点值，去掉那里的RoundToInt，也正是这原因，不能直接调用limits.GetCellIndex()。2）加了一个固定值kPadding(INT_MAX / 4=536870911)。

 }
    return true;
  }

 private:
  static constexpr int kPadding = INT_MAX / 4;
  class GridArrayAdapter {
   public:
    enum { DATA_DIMENSION = 1 };

    explicit GridArrayAdapter(const Grid2D& grid) : grid_(grid) {}

    void GetValue(const int row, const int column, double* const value) const {
      if (row < kPadding || column < kPadding || row >= NumRows() - kPadding ||
          column >= NumCols() - kPadding) {
        *value = kMaxCorrespondenceCost;
      } else {
        *value = static_cast(grid_.GetCorrespondenceCost(
            Eigen::Array2i(column - kPadding, row - kPadding)));
      }
    }

3、2D平移残差块：TranslationDeltaCostFunctor2D

// Computes the cost of translating 'pose' to 'target_translation'.
// Cost increases with the solution's distance from 'target_translation'.
class TranslationDeltaCostFunctor2D {
 public:
  static ceres::CostFunction* CreateAutoDiffCostFunction(
      const double scaling_factor, const Eigen::Vector2d& target_translation) {
    return new ceres::AutoDiffCostFunction<TranslationDeltaCostFunctor2D,
                                           2 /* residuals */,
                                           3 /* pose variables */>(
        new TranslationDeltaCostFunctor2D(scaling_factor, target_translation));
  }

  template 
  bool operator()(const T* const pose, T* residual) const {
    residual[0] = scaling_factor_ * (pose[0] - x_);
    residual[1] = scaling_factor_ * (pose[1] - y_);
残差等于当前平移减去初始平移。残差越大，意味着距离初始位姿越远了。对认为不会和初始偏离太远的场景，越大意味着是真正值的可能性越低。

    return true;
  }

 private:
  // Constructs a new TranslationDeltaCostFunctor2D from the given
  // 'target_translation' (x, y).
  explicit TranslationDeltaCostFunctor2D(
      const double scaling_factor, const Eigen::Vector2d& target_translation)
      : scaling_factor_(scaling_factor),
        x_(target_translation.x()),
        y_(target_translation.y()) {}

  TranslationDeltaCostFunctor2D(const TranslationDeltaCostFunctor2D&) = delete;
  TranslationDeltaCostFunctor2D& operator=(
      const TranslationDeltaCostFunctor2D&) = delete;

  const double scaling_factor_;
  const double x_;
  const double y_;
};

4、2D旋转残差块：RotationDeltaCostFunctor2D

// Computes the cost of rotating 'pose' to 'target_angle'. Cost increases with
// the solution's distance from 'target_angle'.
class RotationDeltaCostFunctor2D {
 public:
  static ceres::CostFunction* CreateAutoDiffCostFunction(
      const double scaling_factor, const double target_angle) {
    return new ceres::AutoDiffCostFunction<
        RotationDeltaCostFunctor2D, 1 /* residuals */, 3 /* pose variables */>(
        new RotationDeltaCostFunctor2D(scaling_factor, target_angle));
  }

  template <typename T>
  bool operator()(const T* const pose, T* residual) const {
    residual[0] = scaling_factor_ * (pose[2] - angle_);
残差等于当前角度减去初始角度。残差越大，意味着距离初始位姿越远了。对认为不会和初始偏离太远的场景，越大意味着是真正值的可能性越低。

    return true;
  }

 private:
  explicit RotationDeltaCostFunctor2D(const double scaling_factor,
                                      const double target_angle)
      : scaling_factor_(scaling_factor), angle_(target_angle) {}

  RotationDeltaCostFunctor2D(const RotationDeltaCostFunctor2D&) = delete;
  RotationDeltaCostFunctor2D& operator=(const RotationDeltaCostFunctor2D&) =
      delete;

  const double scaling_factor_;
  const double angle_;
};