MRI驱动导管设计优化

磁共振引导磁驱动可操纵导管的设计

1 引言

导管消融是一种用于治疗心房颤动的微创技术[1, 2]。在图1(a)中，导管经股静脉和右心房穿过房间隔进入左心房。导管被引导至肺静脉口区域，并利用射频能量在开口周围形成环形病灶。这些病灶形成屏障，阻止引起心律失常的异常电信号扩散。

磁共振成像（MRI）由于具有优异的软组织可视化能力且无辐射暴露，已被证实对导管消融手术的改进至关重要[3]。在导管消融中，MRI既可用于术前获取左心房及相关区域的详细解剖学信息，也可用于术后检测并发症和病灶可视化[4]。已有研究展示了利用MRI进行实时导管引导和病灶可视化[3, 4]。

机器人导管已成为导管消融中的一种有前景的替代方案。其优势包括降低医生的体力要求、减少辐射暴露、提高导管稳定性以及更高的可重复性。MRI驱动导管在[6]和[7]中被提出。图1(b)展示了MRI驱动的可操控导管的一般概念。该导管基于聚合物管材构建，并嵌入一组载流线圈。通过在线圈中通入电流，使其在磁共振成像扫描仪的磁场下产生磁力矩，从而实现导管的偏转。电流可在控制室进行控制，以远程操控导管。因此，利用MRI驱动导管，可以在磁共振成像环境中完成定位映射、远程操控、消融引导和病灶可视化。作者[5, 7, 8]已成功在临床MRI扫描仪内演示了MRI驱动导管的三维偏转。

本文重点研究具有图1(b)所示结构的MRI驱动的可操纵导管的设计优化，以最优地执行左心房消融介入。本文讨论的导管设计优化是指常规临床导管位于左心房内的远端段的设计（图1(a)）。导管主体的其余近端段则需满足不同的设计标准。例如，导管主体的近端部分需要提供结构强度和刚度以方便导管插入，而非提供用于灵巧操控的柔韧性。导管近端段的设计已有充分研究，并且不特定于所提出的MRI引导导管驱动方案，因此不在本文考虑范围内。

该介入的目标是在左心房内围绕每条肺静脉的开口形成一个环形病灶。成功的消融干预要求导管具备足够的工作空间以到达消融靶点，并产生足够的接触力以维持与组织的稳定接触。具有足够接触力(CF)的稳定接触对于形成适当深度的病灶至关重要，有助于提高干预的成功率并降低复发率。

原型设计包括两个子问题：导管的材料选择和线圈执行器的设计优化（包括结构与布置）。Liu等人提出并验证了一种MRI驱动导管的三维(3D)模型[5, 8]。该模型表明，导管偏转与导管结构材料的机械性能相关，例如杨氏模量、泊松比、剪切模量和密度。因此，采用因子设计实验方法[9]进行材料选择，以研究这些性能对性能的影响。导管设计还需要选择执行器参数。导管上的每个线圈组由一组三个线圈（一个轴向线圈和两个侧线圈）组成，如图1(b)所示。需要确定每个线圈的匝数和有效面积，以及线圈组在导管上的位置，以优化导管系统性能。

在本研究中，导管材料选择和执行器参数选择依次进行，以降低设计优化的计算复杂度。导管的可达工作空间通过导管设计可实现的偏转角度范围来量化，并作为设计优化中的性能指标。

通过使用心脏的真实模型，在左心房颤动消融介入的仿真中验证了原型的最终设计，评估了导管尖端到达目标位置的能力以及可实现的接触力。

本文的其余部分组织如下。第2节讨论了以往的研究。第3节回顾了导管在外载荷作用下的偏转模型。第4节介绍了为导管选择合适材料的过程。第5节提出了电磁线圈参数的优化以及线圈位置的选择。第6节展示了导管的性能，第7节给出了结论。

2 相关研究

傅等人[10]总结了以往文献中采用不同驱动方法的主动导管类型。磁驱动是一种有前景且正在兴起的驱动方法。磁驱动的一个优点是能够将驱动装置置于末端，而不是患者体外的近端，从而通过减少回差和摩擦来提高带宽。

穆勒等人[11]回顾了文献中用于磁共振成像引导下导管导航的不同驱动方法。通常采用外部磁场，通过电磁微线圈[6–8, 12–15],、铁磁或磁化材料[16–18]甚至永磁体[19, 20]在导管尖端产生磁力矩或力。

远程可控导管的设计通常根据其在临床任务中的操控性能以及对解剖约束的适应性进行评估。操控性能的特征体现在[11]导管尖端的弯曲角度、达到弯曲所需时间、旋转程度和设计的微型化能力。戈塞林等人[17]量化了当两个铁磁球体之间的距离发生变化时导管的变形，并测量了由梯度变化产生的磁力。塞特卡斯等人[13]测量了在1.5T和3T磁共振扫描仪下改变1.8Fr和5Fr导管上螺线管线圈匝数时导管的偏转角。洛西等人[14]展示了一种用于在实时磁共振成像引导下进行血管内导航的磁力辅助远程控制（MARC）导管。但与[13, 17],这种MARC导管[14]仅针对导管在平面上的操控运动进行了研究。最近，莫夫塔哈尔等人[15]开发了第三代MARC导管，可在多个平面中偏转。

在心房颤动消融手术中，导管尖端与组织之间的接触力已被认为是影响手术结果的重要因素[21, 22]。接触力小于10克（100毫牛）的消融干预相比接触力大于10克的消融干预具有更高的复发率[22]。

据我们所知，文献中尚无先前研究讨论过基于任务和解剖约束的MRI驱动导管设计。在导管尺寸的连续体机器人方面，已有一些早期研究针对同轴管机器人[23–25]，基于解剖约束和手术任务约束进行了设计优化。

3 导管偏转模型

在[5, 26]中建立了所提出的MRI驱动导管在自由空间中的三维偏转运动模型，包括弯曲和扭转。在所提出的运动学模型中，导管被近似为一组有限段（如图2所示）。通过梁理论和伯努利‐欧拉定律[5, 26]求解单个段的变形。然后根据每一段的偏转角建立各段的力/力矩平衡方程。

每段（i ∈{1, ···,N}）的平衡方程如(1)所示，
$$
M_i = R_{i,i+1}M_{i+1} + P_{i,i+1} \times (R_{i,i+1}F_i) + Q_{i,i+1} \times (R_{i,14} W_i),
$$
其中，$M_i$和$F_i$表示作用在ith段上的扭矩和力矢量，向量 $\Delta W_i$表示重量

第ith段中，$P_{i,i+1}$和$Q_{i,i+1}$分别表示在第ith段的坐标系中该段的端点和中心点，而$R_{i,i+1}$表示第ith段两端之间的旋转矩阵。其中，$F_{N+1}$和$M_{N+1}$分别为作用在导管尖端的外力和力矩。每一段（i ∈{1, ···,N}）的变形则由下式给出
$$
S_i \cdot M_i = C_i \cdot X_i,
$$
其中，$X_i$表示第ith段的变形角和扭转角向量，$S_i$表示包含第ith段横截面的截面惯性矩和截面惯性积的矩阵，$C_i$表示考虑材料属性（如杨氏模量和剪切模量）的第ith段的刚度矩阵。偏转模型的具体细节在[5, 26]中说明。

通过磁矩与磁场的叉积可以计算出嵌入在导管上的电磁线圈所产生的磁力矩。例如，若电磁线圈嵌入在第kth节上，则附加的磁力矩$M_k$由下式给出
$$
M_k = \vec{\mu} k \times (R {k,1}B_0),
$$
被添加到(1)式中的kth连杆方程中，其中向量$B_0$表示MRI系统的主磁场相对于基坐标系的方向，而$\vec{\mu}_k$表示导管线圈的总磁化矢量相对于坐标系k的方向。

当导管用于消融时，与表面接触的导管受到来自这些线圈的磁力矩、组织反作用的接触力、接触面上可能存在的摩擦力，以及导管和线圈重量的共同载荷作用（图3）。为了建模接触过程中的导管偏转，已在[5, 26]模型的基础上进行了轻微修改，将作用在导管尖端的接触力纳入最后一段的平衡方程中。因此，从数学上讲，外力$F_{N+1}$的计算如下所示
$$
F_{N+1} = F_{con} + F_{fric},
$$
通过引入接触力$F_{con}$和摩擦力$F_{fric}$。

4 导管材料的选择

典型的消融导管在其轴的不同部分可能具有不同的机械特性，以满足不同的设计要求。因此，导管的不同部分可由不同材料制成。本文的重点是设计位于左心房内的导管远端段（图1(a)）。该段的关键要求是具备足够的柔性，以使导管在进行心房颤动消融时具有良好的可操控性。所选材料还需具备生物相容性。本节重点讨论不同材料对操控性能的影响。

4.1 材料选择的因子设计

导管的操控性能与材料的三种机械性能有关：杨氏模量、泊松比和密度。杨氏模量表征弹性各向同性材料的刚度。泊松比

表1：导管常用材料的机械性能。

材料	密度 (kg/m³)	杨氏模量 （兆帕）	泊松比
聚氨酯	1200	25	0.42
硅橡胶	1100‐2300	1-50	0.47‐0.49
聚四氟乙烯	2160	400	0.46
聚乙烯	950	700	0.42
尼龙	1100	3000	0.42
聚氯乙烯	1400	1500	0.42
聚酰亚胺	1420	2500	0.34
聚酯	1300	3500	0.25
聚醚嵌段酰胺	1000	12‐513	0.34

给出了材料横向应变与轴向应变之间的关系。材料的密度决定了原型在其尺寸给定情况下的重量。

为全面涵盖导管材料，文献中针对导管制造所指定的常用生物相容性材料，例如某些专利[27–29], 中所述，已在表1中进行总结。导管有多种类型，如导尿管、血管内导管、胃肠道导管、血管造影导管，以及用于神经血管和眼科介入的微导管。这些不同类型的导管具有广泛而不同的功能，因此根据其应用需求具有不同水平的刚度值。需要注意的是，有时导管由表1中提到的两种或多种材料组合制成，以实现所需的性能特性。

由于所提出模型的复杂性和非线性，材料属性的影响并不直接。因此，采用析因设计实验方法来分析不同材料属性的影响。因子设计实验方法[9]是一种从统计学角度出发，系统研究两个或更多设计因素对响应变量影响以及因素间交互作用对响应变量影响的方法。本文中研究的因素为密度、杨氏模量和泊松比。实验中各因素的水平在表2中给出。由于这三个因素之间的关系未知，第一次实验考察了较宽范围的属性2，涵盖了表1中列出的所有潜在材料。根据第一次实验的结果，对第二次实验的水平选择进行了优化。

用于评估操控性能的目标函数是导管在自由空间中的可达工作空间。本因子设计实验中使用的嵌有一组线圈的导管模型规格汇总于表3。实验采用临床MRI系统中常见的3T均匀磁场。线圈通过一系列电流依次激励，电流以50毫安为步长递增，且不超过300毫安。此处假设通过采用适当的热管理和散热策略，线圈上的焦耳热可以被有效散发。3线圈段的柔韧性保持固定，在因子设计实验中不发生变化。

4.2 工作空间计算

图4(a)显示了在三维空间中偏转的导管。虚线和实线分别表示零位形（电流为零时）的导管和在某些电流作用下偏转的导管。基坐标系(S)位于导管基部。Z轴沿导管初始主体方向延伸。末端坐标系(T(.))位于导管尖端4，其 Z轴沿导管主体向外延伸。

在图4(a)中，磁场矢量（$B_0$）沿S坐标系的Ys轴方向。重力方向沿导管方向，因为这可以说是变形最严重的配置情况，因为导管需要克服

表2：两次因子设计实验中各因素（密度、杨氏模量和泊松比）的水平

试验	水平	密度 (kg/m³)	杨氏模量 （兆帕）	泊松比
1st	1	800	50	0.10
1st	2	1200	300	0.20
1st	3	1600	1000	0.30
1st	4	2100	2500	0.40
1st	5	2500	3500	0.50
2nd	1	800	5	0.25
2nd	2	950	20	0.30
2nd	3	1100	40	0.35
2nd	4	1200	60	0.40
2nd	5	1300	80	0.45
2nd	6	1400	100	0.50

表3：因子设计实验中使用的导管原型规格。

参数	值
轴向线圈的绕组匝数	130
每个正交侧线圈的绕组匝数	30
总长度	60毫米
导管管体外径	3.18毫米
导管管体内径	1.98毫米
轴向线圈直径	4.45毫米
轴向线圈长度	10毫米
每个侧边线圈长度	10毫米
每个侧边线圈宽度	3 mm
线圈中心距导管尖端的位置	15毫米
导线直径	0.064毫米
导线密度	8940 kg/m³
血液密度	1060 kg/m³
重力常数	9.81

重力 由于工作空间在三维欧几里得空间中的形状通常不是规则形状[3],，因此很难通过将工作空间拟合到任何已知曲面来计算覆盖面积。因此，导管的工作空间通过导管尖端相对于导管初始方向在极坐标下所能达到的所有偏转角范围来表示，如图4(b)所示。偏转角 $\theta$是向量Ztc与向量Zti之间的夹角，偏转角$\phi$是向量Ztc在XtiYti平面的投影与向量Xti之间的夹角。然后将这两个偏转角绘制在极坐标系中，其中以弧度为单位的$\theta$作为半径，以度为单位的$\phi$作为角度（示例见图6）。所形成的闭合曲线（图6(b)）的面积被用作工作空间覆盖面积的量化指标。

4.3 材料选择的结果

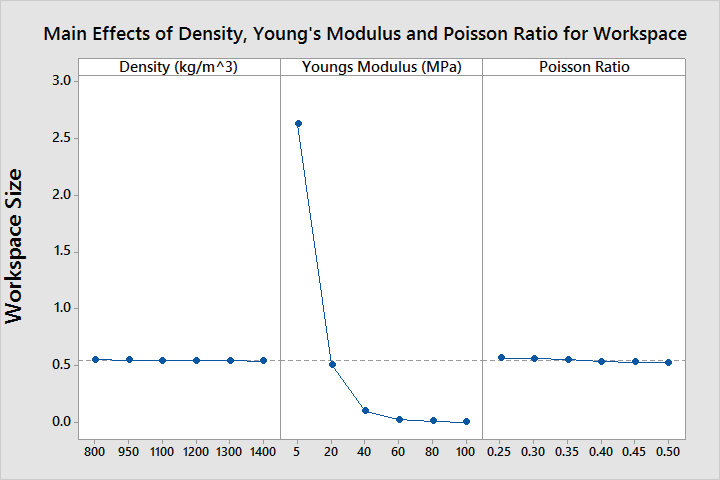
图5(a)显示了第一次实验中各因素的主效应。杨氏模量是影响操控性能的主要因素，特别是在50‐300兆帕的范围内。与杨氏模量相比，密度和泊松比的曲线要平缓得多。但较小的密度值以及位于选定值中间范围的泊松比可以使导管更灵活。本实验缩小了参数的范围

合适的材料，例如聚氨酯、硅橡胶和聚醚嵌段酰胺。第二次实验中各因素的细化水平列于表2。

图5(b)显示了第二次实验中这些因素的主效应。结果表明，较低的杨氏模量范围（5‐20兆帕）具有更好的变形性能。在表1列出的常用于导管构造的材料类型中，聚氨酯、密度较小的硅橡胶以及杨氏模量较小的聚醚嵌段酰胺从导管运动学角度来看是更优的选择。

根据析因设计分析的结果，选择杨氏模量为5 MPa、密度为800kg/m³、泊松比为0.2的材料。图6(a)显示了该导管设计选择的工作空间。蓝色曲线表示偏转后的导管构型，蓝色曲线末端的红色星号表示导管尖端位置。图6(b)以极坐标中的偏转角表示二维工作空间。在此图中，红色星号表示在不同电流水平下获得的偏转角，带有虚线的黑色多边形是包围工作空间的近似多边形。该多边形的面积大小大致表示笛卡尔空间中的实际工作空间。

5 驱动优化

5.1 心房消融任务描述

在MR引导消融手术期间，将一根临床导管插入位于临床MRI扫描仪内的患者体内（图7(a)）。本文中的消融任务是在一个逼真的左心房模型上围绕肺静脉的四个开口创建四个环形病灶[30]（图7(b)）。心房颤动消融要求导管能够到达所需的组织靶点，并以足够大的法向接触力保持表面接触，以形成足够深的

病灶。因此，驱动优化的目标是最大化偏转覆盖范围，同时最大化导管在其末端能够施加的法向接触力。

Ho等人[31]描述了左心房的解剖结构。左心房的心腔（图7(b)）是一个开放的空间，但其内部尺寸有限。本研究中用于验证的左心房模型（如图7(b)所示）直径约为60毫米。Ho等人[31]还指出，内壁相对光滑，因此导管尖端与内壁之间的摩擦系数非常低。

图7(a)展示了患者在磁共振成像扫描仪[30]内的定位方式，以及相对于患者而言的重力和磁场矢量的方向5。相应地，图7(b)显示了心房模型与磁场方向及重力方向之间的关系。

5.2 设计变量

5.2.1 电磁线圈的设计变量

导管偏转的唯一驱动源是电磁线圈产生的磁力矩。众所周知，一个线圈组（图1）可将导管偏转至任意方向。因此，线圈组的结构、线圈组的数量Q以及它们在导管上的位置S直接影响操控性能。

磁场中载流线圈所受的扭矩由以下公式给出
$$
\vec{\tau} = \vec{\mu} \times \vec{B},
$$
其中 $\vec{\tau}$为感应扭矩，$\vec{\mu}$为线圈的磁矩矢量，$\vec{B}$为外部磁场矢量。磁矩矢量$\vec{\mu}$是
$$
\vec{\mu}_i = N_i \vec{A}_i i_i,
$$
全局坐标系由患者坐标系定义。

表4 ：仅有一组线圈时变量及其约束的总结。距离和长度的单位为米 m.

变量	符号	约束
线圈组数量	Q	Q = 1
侧线圈匝数	Ns	1 ≤ Ns ≤ 100
轴向线圈匝数	Na	1 ≤ Na ≤ 300
线圈组离尖端的位置	Sd	5 ≤ Sd ≤ 55
侧线圈长度	Ls	5 ≤ Ls ≤ 50

表5：当存在两组线圈时变量及其约束的汇总。距离和长度的单位为毫米。

变量	符号	约束
线圈组数量	Q	Q = 2
侧线圈匝数（远端）	Nds	1 ≤ Nds ≤ 100
轴向线圈匝数（远端）	Nda	1 ≤ Nda ≤ 300
侧线圈匝数（近端）	Nps	1 ≤ Nps ≤ 100
轴向线圈匝数（近端）	Npa	1 ≤ Npa ≤ 300
远端线圈组的位置（远离尖端）	Sd	5 ≤ Sd ≤ 45
侧线圈长度（远端）	Lds	10 ≤ Lds ≤ 20
两组线圈之间的距离	Dist	10 ≤ Dist ≤ 45
侧线圈长度（近端）	Lps	10 ≤ Lps ≤ 20
长度约束	-	Sd + Lds + Dist + Lps ≤ 55

下标 d, p, s, a 分别表示远端线圈组、近端线圈组、侧线圈和轴向线圈。

其中Ni是ith线圈的绕组匝数，ii是通过ith线圈的电流，$\vec{A}_i$是ith线圈的矢量面积（面积矢量的方向由右手定则确定）。轴向线圈的面积由其直径Da决定，侧线圈的面积由其宽度Lw和长度Ls决定。轴向线圈的直径Da和侧线圈的宽度Lw受限于导管的尺寸。因此，侧线圈的长度Ls和每个线圈的绕组匝数Ni是线圈结构的设计变量。轴向线圈的直径Da设定为5.0 mm，侧线圈的宽度Lw设定为3.0 mm。

需要注意的是，线圈参数的选择存在设计上的权衡。增加线圈尺寸和绕组匝数会提高磁力矩，但同时也会增加线圈重量，导致性能下降，因为线圈执行器在变形过程中必须承载自身重量以及导管主体的重量。此外，由于线圈组具有刚性（大约比导管管体刚性高十倍或更多），增加线圈组的尺寸和数量会降低导管的柔韧性。因此，在更高的驱动功率与更高的柔韧性之间存在额外的设计权衡。为了在这些权衡因素之间实现适当的平衡，有必要对不同水平的设计变量下的导管性能进行具体且定量的评估。

这里假设每个线圈组中的两个侧线圈具有相同的几何结构，并且为了对称性，共享相同的匝数。此外，假设每个线圈组中侧线圈的长度等于轴向线圈的长度。

5.2.2 线圈位置的设计变量

导管长度限制了可放置在导管上的线圈组数量，并进一步约束了轴向线圈和侧线圈的长度。导管在左心房内的总长度设置为60毫米。

本文中，线圈组的最大数量Q设置为2。两组线圈之间的最小间距设置为10毫米，以允许弯曲运动。由于在导管尖端安装了电极，因此必须保持远端线圈组与末端之间的适当距离。本文中该最小距离设置为5毫米。此外，近端线圈组的位置也受到约束，需远离导管基部。本文中该最小距离设置为5毫米。轴向线圈和侧线圈的最大匝数由原型的尺寸约束确定。

表6：最终设计参数汇总。距离和长度的单位为毫米。

变量	Nds	Nda	Nps	Npa	Sd	Lds	Sp	Lps
结果	100	300	100	300	5.19	10.15	20.23	12.68

本文中，优化问题根据线圈组的数量被划分为两个独立的问题。该问题中的设计变量及其约束总结于表4和5。

5.3 目标函数

由于线圈的磁力矩是使导管偏转并对组织提供尖端接触力的唯一驱动源，因此优化问题的目标是最大化磁力矩。当导管与约束表面接触并受其限制时，增加接触力将转化为在无约束表面情况下导管可达工作空间的相应增加。因此，类似于导管材料选择，驱动线圈的设计参数也经过优化，以最大化导管在自由空间中的可达工作空间。

工作空间计算方法在第4.2节中说明。图4展示了导管相对于磁场和重力的设置。每个线圈的最大电流设定为300毫安。

5.4 线圈设计优化结果

使用遗传算法对线圈设计参数进行了优化。原因是导管偏转的数学模型具有非线性，且该优化问题为非凸问题。另一个原因是所选定的设计参数数量较多，且部分设计参数为整数（即绕组匝数）。

对于这两个子问题中的每一个，均使用不同的随机初始猜测多次计算遗传算法优化，以缓解局部最小值问题。

结果表明，具有两组线圈的导管比仅有一组线圈的导管具有大得多的工作空间。所确定的设计参数总结于表6中。

图8(a)显示了笛卡尔空间中最终导管设计选择的工作空间。红色星号表示导管尖端位置。类似于图6(b)，图8(b)显示了由偏转角表示的二维工作空间以及包围工作空间的近似多边形。在此图中，代表θ的最大半径为3.14。换句话说，最大偏转角度为 180°，对应于导管被驱动变形为U形的情况。这种偏转能力有助于执行消融任务。

6 验证结果

在本节中，我们展示了一系列仿真研究，用于验证第4节和第5节推荐的导管原型执行心房颤动消融的能力。

具体而言，在验证研究中，评估了该导管在逼真左心房模型[30]（如图7所示）上执行逼真心房颤动消融任务的能力（即在左右肺静脉周围创建环形消融病灶）。期望该导管不仅能够沿预定的消融路径移动，还能在目标消融位置以必要的接触力抵住心腔表面。为了保证导管的平衡状态，静摩擦力必须位于接触力的摩擦锥之内。

本文中，围绕肺静脉的四个环形消融病灶由每条静脉周围八组离散目标点表示，如图7(b)所示。导管通过房间隔上的进入口进入左心房，其任务是到达目标位置，并通过以适当的电流激励相应的线圈来维持稳定接触。为了实现准稳定接触，导管需要能够在心腔表面产生足够大的法向接触力，同时使接触力的切向分量保持在静摩擦力锥范围内。因此，对于轨迹上的每个目标点，仿真在满足一系列条件的前提下最大化法向接触力，以确保适当的接触，这些条件表示为：
$$
\text{maximize} i | F {con}| \quad \text{subject to} \quad \text{平衡方程}(1-2), \quad F_{fric} \in \text{friction cone}, \quad |P_{tip} - P_{target}| < \text{accuracy}, \quad | F_{con}| > \text{minimum contact force}, \quad F_{con} < 0,
$$
其中i表示所有线圈的电流。此外，在仿真过程中实现了碰撞算法，以确保仅导管尖端与心房表面接触。

在分析中，使用了300毫安的电流限制（每个线圈），最小法向接触力为10克（100毫牛），目标精度为1毫米，静摩擦系数为0.2。此外，分析中还使用了3T均匀磁场。

已计算导管在左上肺静脉（LSPV）、左下肺静脉（LIPV）、右上肺静脉（RSPV）和右下肺静脉（RIPV）消融的所有导管构型，如图所示。

中定义的患者坐标系的坐标。)

图10：本仿真中每个消融靶点上的法向接触力大小。

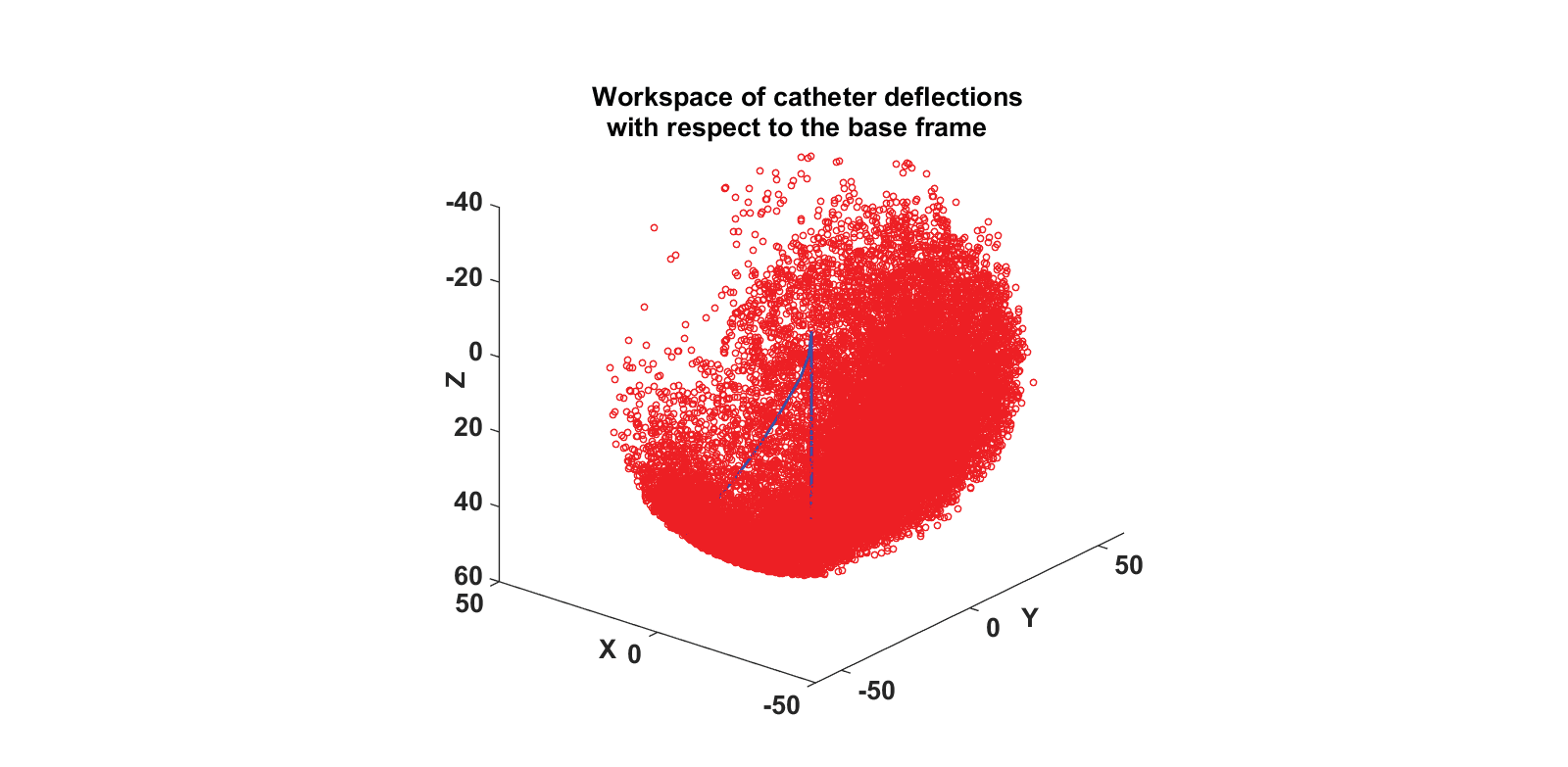
图11：导管原型在插入长度为60毫米时相对于全局坐标系的工作空间。

图9。蓝色曲线表示在左心房内偏转的导管。黑色标记是肺静脉周围的目标位置。

对于每个包含肺静脉开口的圆，优选一个导管插入长度，因为插入动作可能会改变线圈方向与磁场方向之间的关系，这在线圈被激活时会对变形运动产生显著影响。RSPV、RIPV、LSPV和LIPV分别使用了50毫米、49毫米、57毫米和55毫米的恒定插入长度。

验证结果表明，所提出的导管设计能够成功到达所有目标位置，且位置误差在1毫米以内。图10显示了该仿真中各目标点上法向接触力的大小。导管能够为所有RSPV目标以及大多数其他目标产生所需的法向接触力。然而，两个RIPV目标（1st和2nd目标）、一个LSPV目标（3rd目标）以及两个LIPV目标（6th和7th目标）的法向接触力低于目标值10克（100毫牛），但仍明显高于1克（10毫牛）。

图11显示了插入长度为60毫米的导管原型的工作空间。红色圆圈表示导管的尖端位置。工作空间的覆盖范围能够到达肺静脉的开口。一种可能的改进方法是通过使用导丝改变导管基部相对于房间隔上入口处（图11所示的法向量）的方向，从而改善导管对不同目标的可达性。

导管的操控性能取决于通电电磁线圈与扫描仪B0场相互作用所产生的扭矩。在手术过程中，患者的平卧姿势和患者心脏的结构（如图7(a)所示）在很大程度上决定了B0场与心房间隔表面之间的方向关系，尽管心房间隔表面并非一个确定的平面。导管在穿间隔壁上的入口点将对导管的操控性能和受力能力起到重要作用。Jayender等人[32]研究了导管性能与房间隔上不同入口点之间的关系，尽管他们的导管是缆索驱动导管，其驱动方式与任何磁场无关。对于MRI驱动的可操纵导管系统，入口点的选择可以作为未来工作的研究方向。

7 结论

本文提出了一种针对左心房心房颤动消融用MRI驱动的可操纵导管进行设计优化的系统性方法。首先，进行了因子设计实验，以研究导管材料与导管操控性能之间的关系。具体而言，研究了材料机械性能（如杨氏模量、密度和泊松比）的影响。结果发现，杨氏模量是影响导管操控性能最重要的参数。在完成材料选择后，进一步对电磁线圈的设计进行了优化，以选定线圈的最佳绕组匝数、侧线圈的最佳尺寸以及线圈组在导管上的最佳位置。

最后，在逼真左心房模型中通过模拟心房颤动消融验证了所选定的导管设计。仿真结果证实，该导管能够成功到达环形病灶上的各个目标位置。此外，还研究了导管尖端与心腔之间可实现的接触力。对于大多数目标位置，导管至少能提供10克力（100毫牛）。

线圈尺寸与导管偏转之间存在权衡关系。具体而言，由于线圈组比导管主体刚性大得多（刚性大约为10倍或更高），增加线圈组的尺寸和数量会降低导管的柔韧性，同时增加产生的磁力矩。

需要注意的是，电磁线圈中的焦耳热是所提出的驱动方案中的一个重要安全问题。具体而言，在导管设计优化中使用的最大电流值300毫安，当应用于300匝42号线径微线圈时，若未实施任何导管主动冷却或热管理策略，则可能导致线圈中产生显著的焦耳热（从而引起不安全的温升）。本研究尚未明确考虑这一问题，因为产热与散热特性与导管物理结构的具体细节密切相关。可通过多种方法来管理所产生的热量，以防止热量向外传递至周围血液和心腔，并安全地耗散所产生的热量。一些可能的方法包括在线圈上添加隔热涂层以阻止热量外泄、将线圈缠绕在轻质导热体（例如氧化铝基板）上，以及通过导管腔道循环生理盐水冷却剂以主动冷却发热线圈（例如如[33]中所提出的）。该热管理问题是可以解决的，值得在未来进一步深入研究。