改进Kinect骨骼估计精度

改进Kinect骨骼估计

雅库布·瓦尔奇克(B)，扬·谢德米杜布斯基，和帕维尔·泽祖拉
马萨里克大学，博塔尼卡68a，60200布尔诺，捷克共和国 xvalcik@fi.muni.cz

1 引言

微软Kinect 可能是最受欢迎的低成本运动捕捉设备，截至2013年2月已售出超过2400万台。该设备的新版本称为微软Kinect v2（见图1），于2014年推出。

这两个版本均向用户提供了一个软件开发工具包（SDK），可将输入的相机流实时转换为3D运动数据。实时跟踪使得许多复杂的人机交互理念得以应用于各种领域。例如，Kinect 已被用于医疗保健中以监测和改善物理治疗与康复过程 [4,20],在智能家居和公共场所检测老年人跌倒[3,12],在电脑游戏中增强用户与计算机的交互[6,16],在安全领域识别重点关注人员[11,15],或在机器人技术中通过手势控制机器人导航[19]。

不考虑具体的应用领域，由Kinect捕获的运动数据通常通过提取高维特征，并使用基于距离的函数[17]或机器学习方法[2,9]进行比较来预处理。尽管大量努力被投入到设计最合适的特征和比较方法中，但应用的有效性在很大程度上受到准确性的影响。例如，若要仅根据骨骼长度区分不同受试者，则必须以毫米级的准确度捕捉骨骼关节的三维位置。然而，Kinect关节估计的准确性约为 10厘米[13]。如此高的误差只能用于评估运动中的总体趋势，而对于定量估计则需要改进的骨骼化。

P. 泽祖拉——由捷克科学基金会项目编号P103/12/G084资助。

2 相关工作

运动数据采集的原理以及对Kinect v1和v2特性的基本比较在一项广泛调查中给出 [10]。文献 [8]分析了Kinect v1深度数据的底层准确性，以表明需要适当的相机校准，才能在5米距离处实现约4厘米的深度重建精度。在 [1]中评估并比较了两个Kinect版本的旋转精度与制造商提供的规格。该评估显示Kinect v2的旋转精度有所提升，但平均旋转精度误差仍处于1至3。2 的范围。这些发现支持了对更准确的骨骼估计的需求。

多项研究评估了Kinect v1骨骼估计的准确性。Obdrˇz´alek等人[13]在老年人群指导的背景下，比较了Kinect v1与更精确的基于标记的光学设备 Impulse1的关节估计。Fern´andez‐Baena等人[7]开发了一种用于引导式康复治疗的应用程序，并将Kinect v1的可用性与另一款专业基于标记的光学设备 Vicon MX2进行了评估。类似的分析已进行‐

1 PhaseSpace, http://www.phasespace.com[访问于 30/04/2015]. 2 Vicon,http://www.vicon.com[访问于 30/04/2015]。

3 通过Kinect v2进行骨骼跟踪

Kinect v2 能够对位于摄像机源 0.5–4.5m 视野范围内的最多 6 名人体对象进行运动数字化。该运动以每秒 30 帧的频率通过以下四个步骤进行数字化 [10]： （1）获取包含一个或多个人体对象的深度帧流，（2）对深度帧执行背景减除， （3）将提取的对象与大量训练模型进行匹配，以估计当前的骨骼构型，（4） 在估计出当前骨骼构型后推断关节点位置。

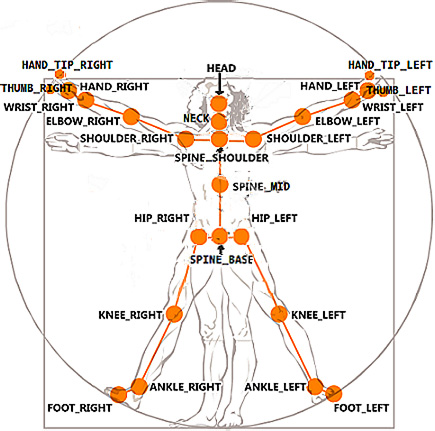
数字化的运动随后由一系列骨骼构型表示，称为姿态。每个姿态描述了25 个人体关节的位置，这些关节在图1中进行了可视化。形式上，
运动 m被定义为一个姿态序列（p1,…, pn），其中 pi（i ∈[1, n]）的 n等于运
动长度（即捕获帧的数量）。每个姿态 pi是一个25维向量（j1,…, j25），包含
对应于特定身体关节的三维真实世界坐标 ji ∈ R3（i ∈[1, 25]）。

根据关节点位置，我们可以测量每种姿态下单个骨骼的长度——只需计算 给定关节对位置之间的欧几里得距离。在理想情况下，特定骨骼的长度不应随 时间变化。然而，图2展示了左胫骨在站立和行走场景中连续90个姿态下的长 度变化情况。两种场景均重复了三次，各次重复分别用红色、蓝色和紫色表示。

即使在静止站立期间骨骼长度变化高达2厘米，行走过程中的误差也超过10厘米， 这一点也在 [13]的结果中得到证实。如此高的不准确性主要是由于拟合了不合 适的训练身体模型以及关节点坐标的估计不精确所致。这种情况促使我们提出 统计方法，以更准确地估计骨骼长度。

4 改进SkeletonProportions估计

由于关节坐标估计不准确，骨骼比例会随时间变化，这一点在前一节关于左胫 骨长度浮动的讨论中已得到证实。此外，当受试者处于运动状态（例如行走） 时，这种变化性相较于静止站立时会进一步增加。因此，仅通过测量就确定给 定受试者骨骼长度具有很高的风险。

从第一（或随机选择的）运动姿态中的骨骼构型。为了更接近受试者的“真实 基准”，我们提出考虑以下四个方面，这些方面可以显著提高骨骼化的准确性。

1. 测量 – 应用统计度量（如平均值、中位数或标准差）来估计在足够具有代表
   性的一组姿态中骨骼的长度，而不是仅考虑单次随机选择的姿态。2. 运动范围
   – 检测语义上有意义的运动片段，例如左/右脚步或步行周期，这些片段相比 随机选择的姿态能提供更准确的骨骼比例信息。3. 运动重复 – 在单次运动中聚 合多个相同类型的运动片段。多个运动实例可比单次运动提供更准确的信息。
2. 运动方向 – 确定相对于Kinect位置的运动方向。特定骨骼的长度在某一方 向上相对于摄像机源的变化远大于其他方向。

通过考虑这些方面，我们提出了简单和高级的骨骼估计方法，特别关注行 走场景。在介绍个体方法之前，我们更详细地描述了上述方面。

4.1 改进的骨骼化方面

本小节介绍了将在特定方面中使用的支持技术，以供所提出的简单以及高级骨骼化 方法使用。

测量。 为了简单估计给定对象的骨骼比例，从（1）第一个或（2）一个随机运 动姿态中选择，并计算其中的骨骼长度。由于第一或随机姿态可能包含关于骨 骼比例的误导性信息，我们建议在每个姿态中计算骨骼长度，并对计算出的距 离应用常见的统计度量，例如（3）平均值、（4）中位数和（5）模式。尽管这 些测量方法易于实现且不需要任何特殊预处理，但它们本身无法利用所执行运 动类型及其重复次数的相关知识。

运动范围。 我们提出分析输入的运动，以识别其语义上有意义的运动片段，例 如脚步和步行周期，并利用这些信息实现更准确的骨骼估计。我们使用“运动 范围”这一术语来表示用于估计比例的运动层次。具体而言，我们在以下三个 层次上估计比例：(1) 完整运动、(2) 左或右脚步以及 (3) 完整的步行周期，即 从行走运动中提取出的左脚步及其后续的右脚步。为了自动提取脚步/步行周期， 我们应用了一种增强版的步行周期检测算法 [18]。将该算法应用于完整运动时， 我们可以获得多个运动片段，具有以下优势：
‐ 检测到的片段不应包含由于身体部位遮挡和光线条件差导致身体模型拟合和 关节坐标估计效果极差的边缘或变形姿态；
‐ 高级骨骼化方法可从特定片段类型及其在单次运动中的多个出现中获益。

运动重复。 同类型运动的多次出现使得能够确定“平均”和“异常”的运动片 段。通过滤除异常值，高级方法被认为可以从更相似的片段中更准确地估计骨 骼长度。为了更深入地分析步行周期的片段，我们进一步将每个步行周期归一 化为固定长度的 n¯姿态，其中n¯= 32对应于平均步行周期长度。该过程通过 缩短或延长长度为 n的每个步行周期来实现，使得其第 i个姿态对应于归一化
片段的第 i· n¯ n 个姿态，类似于 [14]。

运动方向。 通过研究多个步行周期的特征，我们发现受试者相对于Kinect行走 的方向对骨骼化准确性有很大影响。此外，某些骨骼的长度在一个方向上的波 动远大于其他骨骼，而在相反方向上则相反。基于这些发现，我们定义了步行 周期

4.2 高级骨骼化方法

我们使用“简单方法”这一术语来表示骨骼化方法，这些方法将特定测量应用于给定范围内的运动，而不考虑运动重复及其方向。本文提出并评估了25种简单方法的变体，以及8种高级方法的变体。

高级方法主要通过分析行走动作中检测到的归一化步行周期段来估计骨骼 比例。由于每个归一化步行周期的长度相同，因此可以在多个步行周期之间比 较同一运动阶段中给定骨骼的长度，而不是独立地分析每个步行周期内的骨骼。

形式上，我们将m=(p1,…, pn¯)表示为恰好由 n¯个姿态组成的行走周期。对于 由一对关节索引 j1和 j2指定的给定骨骼，我们通过以下函数计算其在第f个姿 态中的长度：
pose bone lengthj1,j2(pf)= ||cj1, cj2||,
其中j1, j2 ∈[1, 25], f ∈[1, n¯]和 cj1, cj2是姿态pf=(c1,…, c25)的3D关节坐标，
基于欧几里得距离计算它们之间的骨骼长度。通过这种方式，我们可以计算同 一运动阶段中每个步行周期的骨骼长度。通过对 l个归一化步行周期组成的集
合M={m1,…, ml}计算骨骼长度，我们得到第 f个姿态下的骨骼长度集合 Bj1,
j2(f, M)：
Bj1,j2(f, M)={pose bone lengthj1,j2(pf)| ∀m ∈ M: pf ∈ m}.
每个 B集合中特定骨骼的长度在理想情况下应相等，因为它们是在多个步 行周期实例中的相同运动阶段计算得出的。然而，实际情况与此相差甚远—— 图3展示了在8个步行周期实例上测量的左胫骨长度的变异性，这些数据已归一
化至 n¯= 32姿态。为了尽可能准确地确定骨骼长度，我们仅考虑 F由 k重要
运动阶段 F={f1,…, fk}（k ∈[1, n¯]）组成的集合，其中变异性应较小。最终
通过在所有重要运动阶段中对骨骼长度取平均值来计算得到骨骼长度：
bone lengthj1 , j2(F, M)=
∑f∈ F∑b ∈ Bj 1 , j 2 (f ,M)
b
|F| · |M| .

0.25
0.3
0.35
0.4
0.45
0 5 10 15 20 25 30
Bo ne le ng th (m )
时间（姿态）
图3. 在8个归一化为32个姿态的步行周期中测量的左胫骨长度的变异性。每个步行周期 的变异性由灰色虚线表示，而红色线条表示平均值，相应的标准差以粉色条形表示。蓝 色箭头表示检测到的十个（k= 10）重要运动阶段，这些阶段的标准差最小。

为了确定 k重要运动阶段，我们提出了以下两种方法：基于骨骼长度的标准差 最小化和关节速度的最小化。

多个步行周期中的标准差最小化

该方法通过计算每组骨骼长度的 n¯骨骼集合 B的标准差来选择所需的 k姿态。
目标是仅考虑标准差最小的骨骼集合。标准差越小，骨骼长度被正确确定的概 率越高。第 f个姿态中关节 j1与 j2之间骨骼的标准差计算公式为：
bone std devj1,j2(f, M)=√ ∑b∈B j1 , j2(f,M)( b− bavg) 2
|M| ,
其中 bavg是输入骨骼集合 Bj1内j2（f， M）的平均骨骼长度。 k由于每个骨骼 集合的标准差被计算出来后，这些集合按标准差升序排列，因此前 k个集合对 应的特定姿态被视为重要运动阶段。在图 3中， k= 10从8个行走周期实例中 识别出重要阶段。

多个步行周期中关节速度的最小化

选择 k重要运动阶段的另一种方法是基于测量关节速度。其动机是确定测量骨
骼移动最慢的时刻。骨骼移动越慢，Kinect关节估计就越准确。要计算joint
velocity，我们

582 J.Valcik 等人

测量关节在一个姿态中移动的欧几里得距离。该骨骼在第 f个姿态中的骨骼速 度定义为确定该骨骼的两个关节 j1和j2速度的最大值：
bone velocityj1,j2(f)= max{||cj1 ∈ pf, cj1 ∈ pf+1||, ||cj2 ∈ pf, cj2 ∈ pf+1||}.
在计算每个运动姿态的骨骼速度后，我们通过给定姿态中测量的骨骼速度的中 位数来确定多个步行周期内的姿态速度。与之前的方法类似，所有步行周期的 姿态按照其速度升序排列，并选择最慢的前 k个姿态作为重要运动阶段。

5 实验评估

我们评估了若干种提出的简单和高级方法的变体，这些方法通过行走动作来估 计骨骼比例。这些方法结合了测量、运动范围、运动重复和方向的不同方面。
评估基于将各个方法的结果与为每个受试者测量的骨骼真实值进行比较。

5.1 数据集

所有实验均基于我们使用微软Kinect v2设备采集的自建数据集进行评估。该数 据集包含10名受试者（9名男性和1名女性，年龄25–67岁，身高164–188厘米） 完成的270个动作序列。每名受试者在7种不同的运动场景下进行记录，这些场 景主要关注在不同距离和方向上站立与行走时身体比例的测量。所有场景如表 1所示，其中方向值为北（N）、东（E）、南（S）和西（W）的缩写。各个场 景包含三种不同的运动类型：（1）T型姿势指受试者站立，双腿微微分开，手 臂伸展肘部弯曲，手指向上；（2）掉头指受试者直接朝向设备行走，在设备
前方约0.5米处执行掉头（右或左），然后沿相反方向继续行走；（3）对角线
行走指从Kinect视野范围的一个远处角落走向靠近设备的对角角落，即从东北 角走向西南角，或从西北角走向东南角。

5.2 真实值

我们创建的真实值包含每个受试者的骨骼比例——即骨骼长度。具体而言，我 们仅关注9个主要骨骼：左右胫骨、左右股骨、左右肱骨、左右桡骨以及髋宽。
由于大多数关节中心位于体内，精确测量骨骼长度是一项复杂的任务。因此， 我们直接根据采集的数据构建真实值。

改进Kinect骨骼估计 583

表1. 10名受试者执行的运动场景。

运动类型	方向	距离	重复次数
T型姿势	S	1.5 米	3
T型姿势	S	2 m	3
T型姿势	S	2.5 米	3
右转掉头	S, N	0.5–4.5 米	3
左转掉头	S, N	0.5–4.5 米	3
东南对角行走		0.5–4.5 米	6
西南对角行走		0.5–4.5 米	6

Kinect。为了实现骨骼长度随时间的低方差，真实值仅从T字姿势计算得出 （见表1）。在T字姿势中，左侧胫骨长度的平均标准差为0.022米，而掉头和对 角线行走的平均标准差分别为0.064米和0.084米。

然而，T字姿势下的标准差为2.2cm仍不理想。该误差主要由捕捉开始阶段 骨骼拟合不准确引起。为了进一步提高测量的骨骼长度的准确性，我们提出进 行约10秒的T字姿势场景，并定位其中特定骨骼长度变化较小的3秒部分。这种 合适部分的选择通过一个3秒长的滑动窗口实现，该窗口用于寻找标准差最小的 动作片段。在为各个骨骼定位到这些片段后，其特定骨骼长度将根据对应定位 窗口内的中位数计算得出。通过对Kinect不同距离下（三种距离各重复三次） 共九次记录的T型姿势站立场景进行分析，真实骨骼长度被确定为这9次测量值 的中位数。由此获得真实骨骼比例。

5.3 简单与高级骨骼化方法的评估

通过对估计的骨骼比例与真实值骨骼比例之间的平均绝对误差（MAE）和平均 相对误差（MRE）进行测量，评估了所提出的简单和高级方法的变体。结果如 表2所示，该表综合了不同变体的测量方式、运动范围、动作重复次数和方向， 以及跟踪状态。由于Kinect提供了特定关节是否被正确跟踪的信息，我们扩展 了所提出的方法，针对特定骨骼估计，忽略那些关节未被正确跟踪的姿态。此 行为对应于表=2中“Tracked是”标志。结果显示，简单方法的误差较高，例 如，在首次和随机运动姿态下估计骨骼比例的MAE分别为0.041 m和0.038 m。此外，简单方法的绝对误差变化较大，平均MAE超过0.030m。其中最佳 简单方法是对所有运动姿态下的骨骼长度取平均，其MAE为0.021 m，相对误 差为8.5%。另一方面，高级方法（检测 k= 10和 k= 16重要阶段用于

584 J.Valcik等

表2. 简单和高级方法的33种变体对每个受试者的真值骨骼比例进行估计所得的骨骼比例 的平均绝对误差（MAE）和相对误差（MRE）。

测量	范围	跟踪	重复	方向	MAE（米）	MRE（%）
第一	运动	Yes	单次	No	0.041	14.4%
第一	运动	No	单次	No	0.041	14.5%
第一	NWC	No	单次	No	0.032	11.8%
第一	LF	No	单次	No	0.033	12.2%
第一	RF	No	单次	No	0.033	12.5%
随机	运动	No	单次	No	0.034	12.7%
随机	运动	No	单次	No	0.038	14.4%
随机	NWC	No	单次	No	0.034	12.8%
随机	LF	No	单次	No	0.035	12.8%
随机	RF	Yes	单次	No	0.036	13.3%
Mode	运动	No	单次	No	0.034	12.5%
Mode	运动	No	单次	No	0.037	13.7%
Mode	NWC	No	单次	No	0.034	12.8%
Mode	LF	No	单次	No	0.035	13.0%
Mode	RF	Yes	单次	No	0.037	13.6%
中位数	运动	No	单次	No	0.023	9.3%
中位数	运动	No	单次	No	0.025	9.9%
中位数	NWC	No	单次	No	0.028	11.0%
中位数	LF	No	单次	No	0.030	11.6%
中位数	RF	Yes	单次	No	0.032	12.0%
平均	运动	No	单次	多个	0.021	8.5%
平均	运动	No	单次	多个	0.022	8.9%
平均	NWC	No	单次	多个	0.025	10.0%
平均	LF	No	单次	多个	0.028	10.7%
平均	RF	Yes	单次	多个	0.028	11.1%
标准差最小化	NWC	No	多个	No	0.021	8.6%
标准差最小化	NWC	Yes	多个	No	0.022	9.0%
标准差最小化	NWC	No	多个	Yes	0.018	6.7%
标准差最小化	NWC	Yes	多个	Yes	0.018	6.8%
速度最小化NWC	No	多个	No	0.022	8.7%
速度最小化NWC	Yes	多个	No	0.021	8.5%
速度最小化NWC	No	多个	Yes	0.017	6.5%
速度最小化NWC	Yes	多个	Yes	0.017	6.6%

标准差最小化和速度最小化方法的平均绝对误差（MAE）均在约0.020 m附近， 变化较小。通过考虑行走方向、跟踪的姿态以及多个步行周期实例，可获得最 佳结果——标准差最小化和速度最小化方法的MAE均达到约0.017 m，平均相 对误差（MRE）低于7%。

我们进一步分析了高级方法，以确定相对于各个骨骼而言最适合进行骨骼
估计的行走周期阶段。通过分析速度最小化方法（设置“方向=是”和“跟踪=
是”），我们在图4中可视化了在归一化步行周期内检测到的重要运动阶段的位 置。该图针对每个受试者，分别对各个骨骼独立检测出的10个最重要的运动阶 段（即， |F| = k= 10）进行了可视化。我们可以观察到，重要阶段通常集中 在行走周期的三个部分，其中

改进Kinect‐骨骼估计 585

双脚交汇并经过，即这些阶段不发生在双支撑姿态及其附近区域。我们还可以 看到，左右骨骼对通常形成互补式分布，例如右前臂的重要阶段位于行走周期 的开始和结束部分，而左前臂的重要阶段则集中在中间部分。总之，该图展示 了在特定骨骼上进行测量时应考虑的方向和行走周期阶段，以使测量尽可能准 确。

6 结论

我们专注于微软Kinect v2设备估计的骨骼比例的准确性。通过分析站立和行走 场景中的数据，我们定义了四个对骨骼化效果具有重要影响的方面。这些方面 使我们能够提出几种高级骨骼化方法的变体。这些方法在实验中与简单方法进 行了比较，显示出超过两倍的有效性提升——仅采用第一姿态或随机姿态时， 绝对骨长误差约为4厘米，而高级方法可将误差降低至仅1.7厘米。此外，我们 分析了高级方法的特性，并可视化了需要测量特定骨骼的重要步行周期阶段。
因此，我们强烈建议在估计骨骼长度时考虑运动方向、左右骨骼对以及双脚交 汇的步行周期阶段，以显著提高准确性。未来，我们计划对骨长误差分布进行 统计建模，以进一步增强骨骼估计，并在不同运动场景（例如改变行走速度） 下分析所提出方法的鲁棒性。