文章介绍了人工智能的基础，通过小蓝生物的故事引入，阐述了如何用一元一次函数描述直觉，并解释了McCulloch-Pitts模型如何模拟神经元。接着，文章详述了Rosenblatt感知器如何通过误差校正实现参数调整，使神经元具备学习能力。编程实验部分展示了如何用Python实现感知器，证明了通过调整权重能提高预测准确性。
目录
一、引言
有人说我们是上帝的作品，也有人说我们自己就是上帝，但我认为把人作为中心讨论却大可不必，因为地球上有那么多的生物智能，又何必是人？不如让我们看看那些更加原始和简单的生物遇到的问题和他们具有的智能。在很深很深很深的海底，住在一个简简单单的生物小蓝，它的世界很简单，去寻找周围能够吃到的一种叫做豆豆的食物，并靠此生存。
但是这些豆豆在漫长的演化历史中，通过和小蓝的反复博弈，为了保护自己，逐渐进化出了毒性，毒性的强弱和豆豆的大小有关系，而小蓝也进化出了一个能够检测豆豆大小的器官。那么问题来了，小蓝如何根据豆豆的大小判断它到底有多毒？
没错，它还缺一个思考的器官，也就是我们常说的脑子。但我们又如何去描述思考或者说认知？认知以前当然就是一无所知。这种情况下，认知事物唯一的方法就是依靠直觉。那我们又该如何去描述直觉？很明显是函数。为什么是函数？仔细想想，我们本来一直就在用函数认识这个世界。在物理中，一个质量为M的物体在不同的受力F下产生加速度a，这是一个以F为自变量，M为参数、a为因变量的函数F=ma。在经济学中，我们把消费、投资、政府购买和进出口作为自变量，也可以形成一个关于GDP的认知函数GDP=f(C,I,g,nx)。实际上，除了这些严格的领域，在很多不那么严格的事情上，如果你愿意，其实也可以用函数去描述认知。比如气温对人心情的影响可能是这样的一个函数
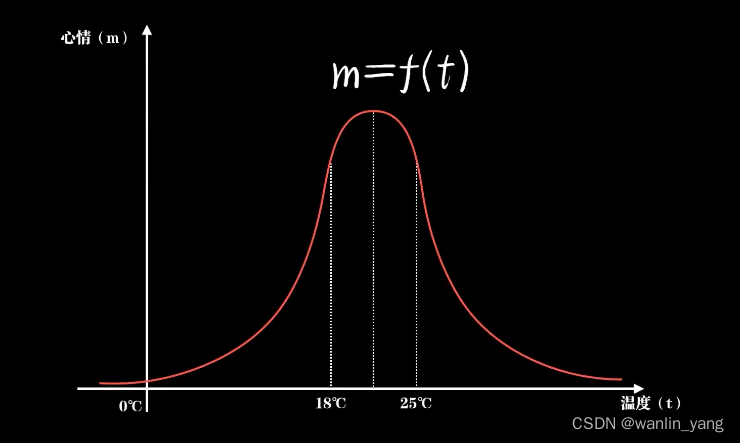
一只小狗的眼睛大小和它可爱程度的关系可能是这样的一个函数，而后者这种不严格、人类更加擅长的问题，也就是我们人工智能要解决的问题，找到一个恰当的函数去描述它。如此这般，把智能体对世界认知的过程看作是在脑中不断形成各种函数。
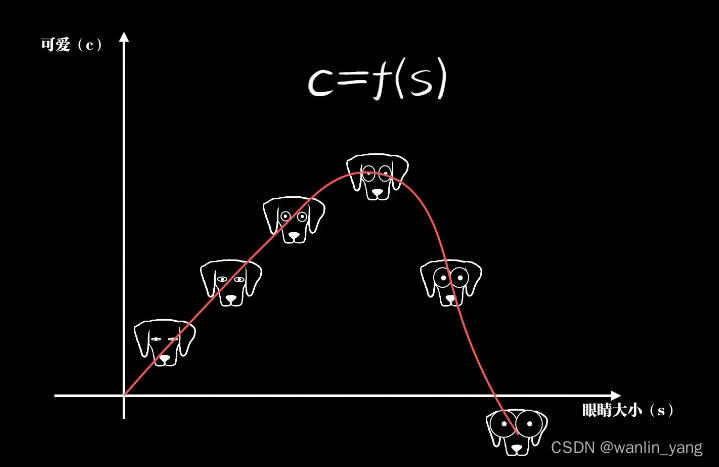
既然是直觉，那么就不需要太多的理由，豆豆的毒性和它的大小有关系，所以这里的直觉自然是一个一元一次函数，豆豆的大小X是自变量，毒性Y是因变量，而W是一个确定的参数，也就是我 们常说的直线的斜率。
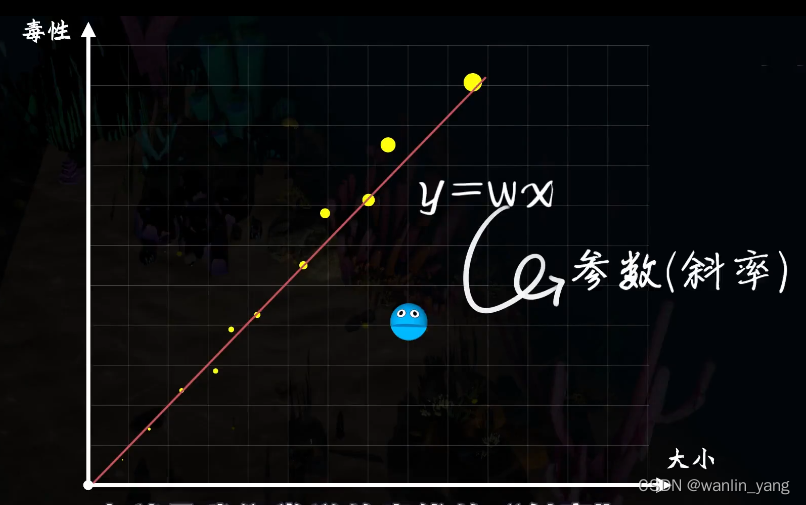
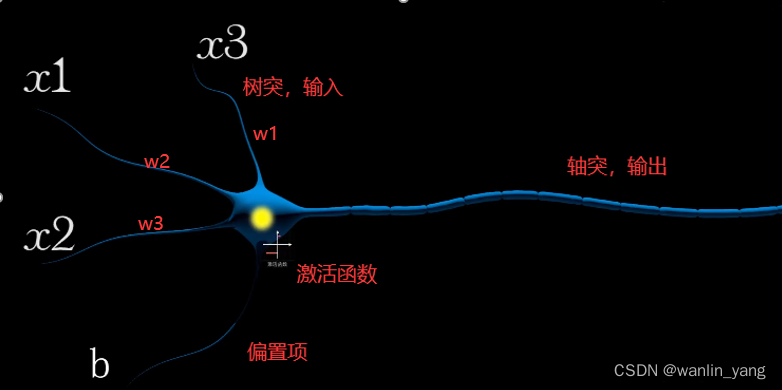
二、McCulloch-Pitts模型
一个简单的一元一次函数就可以描述一个直觉，建立一种思考的模型。当我们去类比生物神经元的时候，你就会发现，用一个一元一次函数去描述认知可不是乱用的，完全是有备而来。这实际上就是早
最低0.47元/天 解锁文章
扫一扫
916
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
