11.人工智能原理-卷积神经网络：图像识别实战

目录

       ​一、卷积运算

       二、池化层

       三、编程实验

       四、总结

       五、往期内容

---

一、卷积运算

       上节课我们已经了解到卷积操作是怎么一回事，那接下来我们就看看如何把卷积运算融入到我们的神经网络之中。我们还是以上节的“5”为例：

       这是一张8*8的灰度图，用一个3*3的卷积核对它进行卷积，输出一个6*6的结果，我们把这个做卷积运算的一层称为卷积层。卷完以后我们把结果拆成一个数组，送入到后面的全连接层神经网络中。

       那么问题来了，卷积核中的各个值是多少呢？实际上，我们不必管它，随机初始化这些值就好，卷积核的值也是通过训练学习而来的，通过训练找到合适的卷积核去提取不同的特征。

💡那么如何卷积核反向传播调整参数呢？

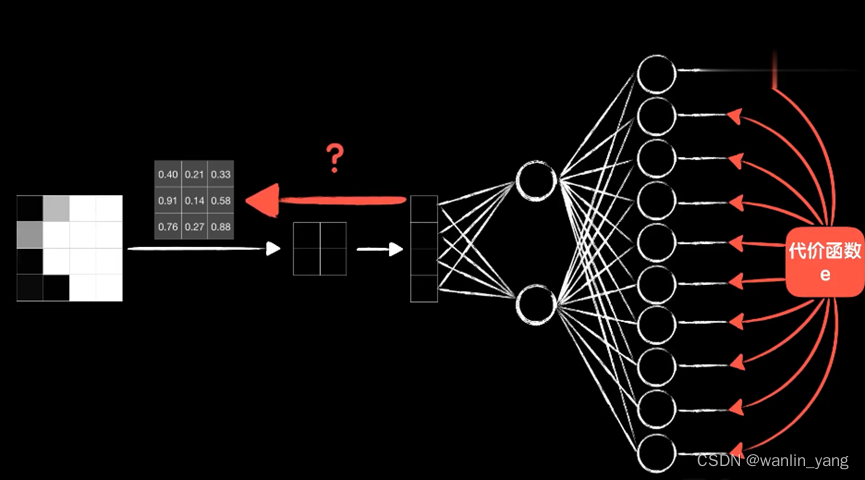
       minst数据集是10分类的问题，所以输出层有10个神元。

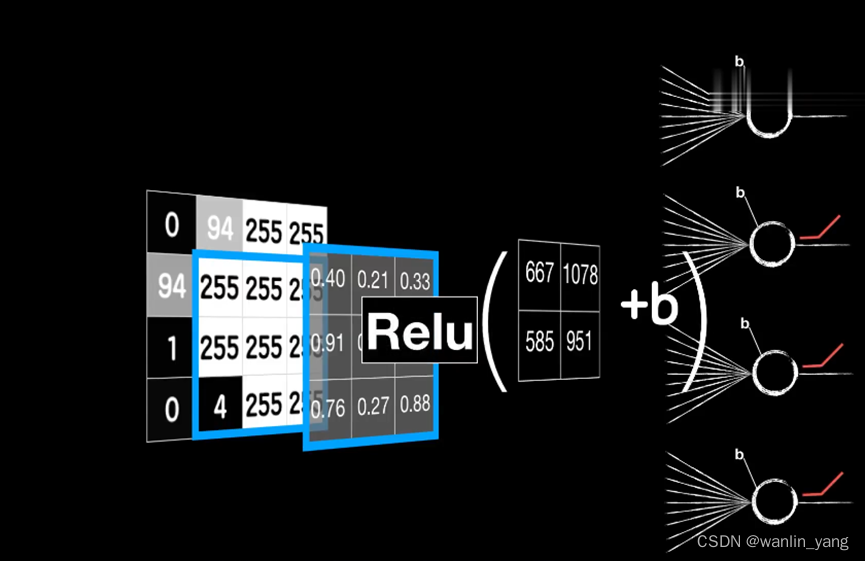
       卷积的过程：卷积核依次和这些小图（局部数据）对应元素相乘再相加得到一个值，可以类比之前讲的普通神经元。神经元的线性函数再加一个偏置项B，然后通过激活函数进行非线性运算，这才是卷积层的最终输出。

       这样我们就把一个卷积层拆成了4个普通的神经元，我们就可以像之前在普通神经元中那样，很轻松地继续把误差代价反向传播下去。

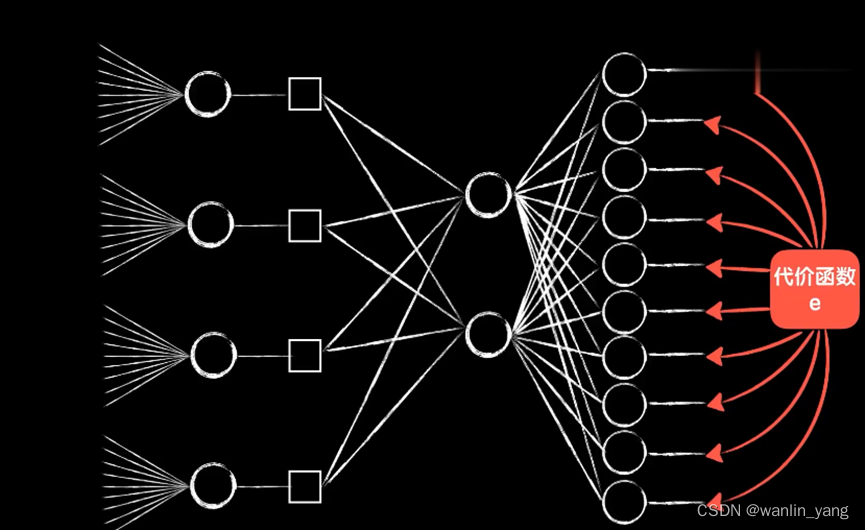
注意以下几个细节：

1.首先这四个神经元的输出是根据卷积的过程排列而成的二维的结构，所以我们在送入全连接层时需要手动进行平铺。

2.然后这四个神经元的输入并不相同，实际上是同一个图片的不同区域

3.最后这四个神经元的权值参数并不是独立的，它们都来自同一个卷积核，所以实际上它们的权值参数（包括偏置项b）是一样的，我们只是把一个东西强行拆开平铺成4个。也就是说这四个神经元复用了同一套权重参数，这就是所谓的