Neural Relational Inference for Interacting Systems摘要

摘要

  在自然中，互相作用的系统是非常普遍的，从物理中的动力学系统，到社会动力学系统，各组件之间的相互作用可以产生复杂的动态结果。作者描述了一种neural relational inference (NRI) 模型：一种从观察数据中学习动力过程时还能进行关系推断的无监督模型。这个模型采用一种自适应编码的形式，用潜编码表示图中的潜在关系，用GNN进行图的重建。在一个基于物理模拟系统的实验中，作者表明NRI模型能以无监督方式推理出相互作用关系。而且证明了，在复杂动作捕捉和运动追踪中，可以发现可解释的图结构并进行预测。

介绍

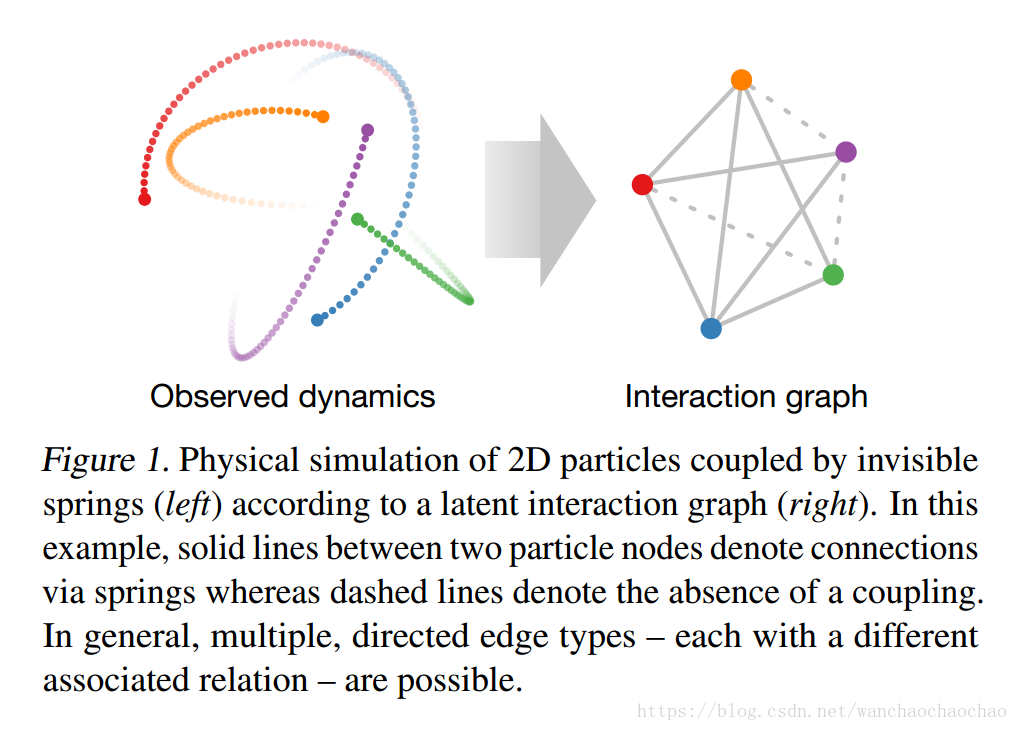
  物理、生物、运动及其它领域的动力学系统能被看成是一组相互作用的组件，从而产生整体上的复杂动态结果。对这种动力学系统建模是困难的，因为我们只知道整体的数据，并不知道潜在相互作用或动力学过程。为此考虑一个篮球运动的例子，每个球员都会受其他球员影响，影响关系有防某个球员或掩护队友等。可以人工标注出特定的相互作用方式，但是更好的方式是以无监督方式学习潜在的相互作用方式。最近有很多使用隐式相互作用的模型来学习这种动力学系统。这种模型称为GNN，通过全连接图传播信息，用message passing来隐式的对相互作用进行建模，或者再用上注意力机制。作者在此所提出的问题是，在无监督方式下，学习动力学模型的同时推理出显式相互作用的结构。NRI使用GNN在潜在离散图上进行学习，并在潜在变量上进行推断。推断的边的类型对应一族相互作用，使用概率模型允许我们引入稀疏性等图结构的先验信息。

GNN背景

  GNN及变体能高效的执行关系推断、相互作用的关系建模、多代理系统、图分类、节点分类等任务。给定一个图$\mathcal{G}=(\mathcal{V},\mathcal{E})$，节点$v\in\mathcal{V}$，边$e=(v,v')\in\mathcal{E}$，先定义GNN中一个点对点操作：

$$v\rightarrow e:h_{(i,j)}^l=f_e^l([h_i^l,h_j^l,x_{(i,j)}]) \tag{1}$$
$$e\rightarrow v:h_j^{l+1}=f_v^l([\sum_{i\in\mathcal{N}_j}h_{(i,j)}^l,x_j]) \tag{2}$$
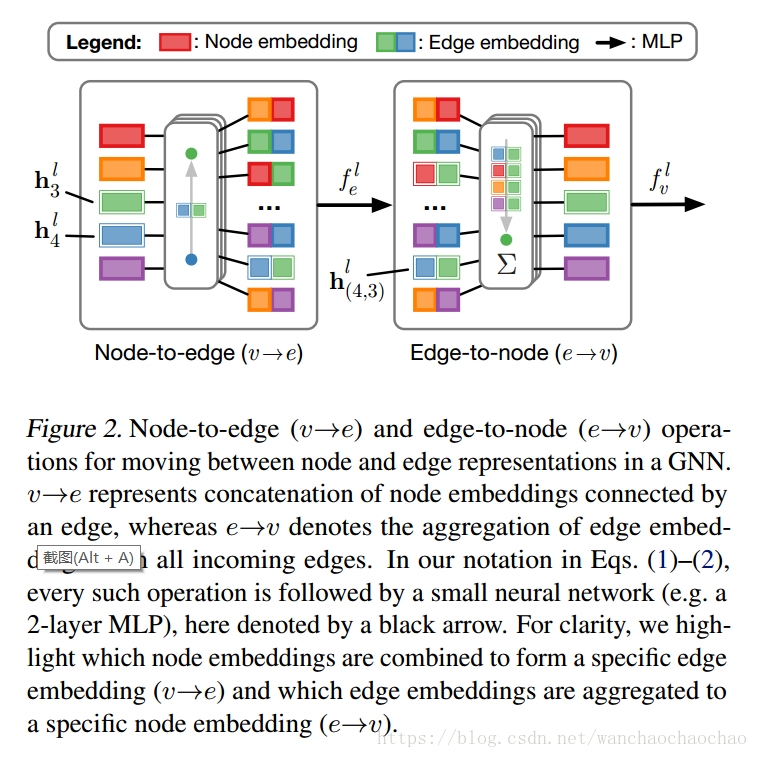
$h_i^l$是 $l$层节点$v_i$的嵌入， $h_{(i,j)}^l$是边 $e_{(i,j)}$的嵌入， $x_i$和 $x_{(i,j)}$是节点和边的原始特征。 $\mathcal{N}_j$记为入边对应的指标集， $[\cdot,\cdot]$记为向量串联符号。 $f_v$和 $f_e$是产生节点和边的neural网络。将 $f_v$和 $f_e$以多层message passing的方式组合起来，每层执行从边到节点的映射，或从节点到边的映射。在原始GNN中，节点嵌入 $h_i^l$只取决于 $h_{(i,j)}^l$，发射节点嵌入，以及边属性，但不包括接收节点嵌入。最近有的工作里面将 $f_e^l(\cdot)$分成两个独立的部分，其中一个有注意力机制的作用，在有的时候会引入良好的归纳偏置。

NRI模型

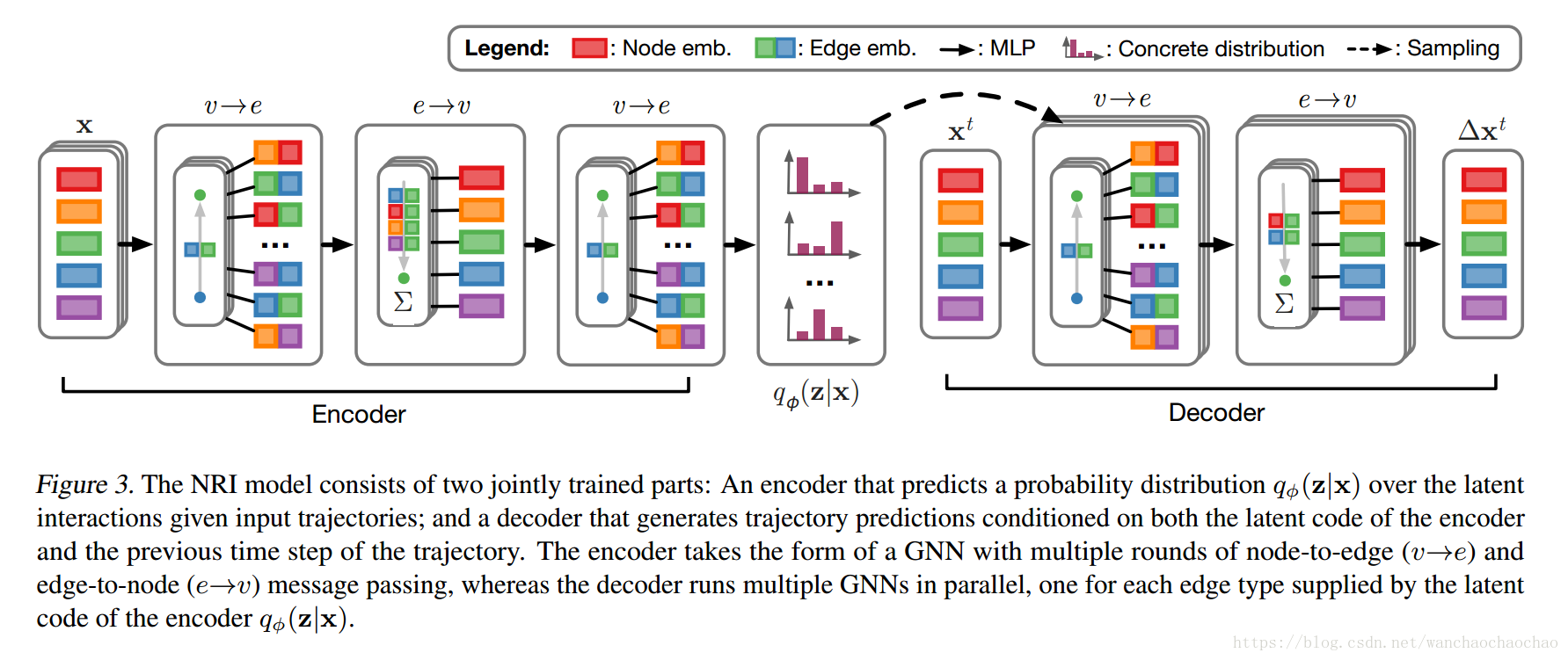
我们的NRI模型有两个共同训练的部分组成：编码器在给定动力系统的历史数据后预测相互作用，以及一个解码器在给定相互作用的图结构后学习动力系统的模型。输入由$N$个节点组成，在$t$时刻将节点$v_i$的特征向量记为$x_i^t$，所有$N$个节点的特征集记为$x^t=\{x_1^t,\dots,x_N^t\}$，$x_i=(x_i^1,\dots,x_i^T)$记为节点$i$的历史轨迹，最后所有历史轨迹数据记为$x=(x^1,\dots,x^T)$。作者假设，GNN能够在不知道$z(其中z_{ij}代表v_i和v_j之间的边的离散属性值)$。这里的任务是，以无监督的方式，在学习动力系统建模的同时预测边的属性值。
  这个模型表述为变分自编码器(VAE)的形式：

$$\mathcal{L}=\mathbb{E}_{q_\phi(z|x)}[logp_\theta(x|z)]-KL[q_\phi(z|x)\parallel p_\theta(z)] \tag{3}$$

编码器

  编码器的目标是根据时序数据$x=(x^1,\dots,x^T)$，推断出$z_{ij}$，其中$z_{ij}$代表$v_i$和$v_j$之间的相互作用的关系类型。由于不知道潜在的图结构，所以使用一个全连接的GNN预测潜在图结构。编码器表示为$q_\phi(z_{ij}|x)=softmax(f_{enc,\phi}(x)_{ij,1:K})$，其中$f_{enc,\phi}(x)$全连接的无环图。给定数据$x_1,\dots,x_K$后，编码器计算message passing操作：

$$h_j^1=f_{emb}(x_j) \tag{5}$$
$$v\rightarrow e:h_{(i,j)}^1=f_e^1([h_i^1,h_j^1]) \tag{6}$$
$$e\rightarrow v:h_j^2=f_v^1(\sum_{i\ne j}h_{(i,j)}^1) \tag{7}$$
$$v\rightarrow e:h_{(i,j)}^2=f_e^2([h_i^2,h_j^2]) \tag{8}$$
最后，边的属性值的后验为 $q_\phi(z_{ij}|x)=softmax(h_{(i,j)})$，其中 $\phi$记为neural网络的参数。这样多个message passing的方式可以解决多重相互作用的问题，在单步passing时边的嵌入 $h_{(i,j)}^1$只取决于 $x_i$和 $x_j$之间的相互作用，而到了 $h_j^2$就开始利用到了整个图的信息。这里的 $f_{(\dots)}$可以是全连接网络(MLP)或一维卷积网络(CNN)。这里有一点和原来的GNN是不同的， $h_{(i,j)}^l$不再只是计算过程中的一部分，而是作为一个整体代表边的分类属性的一种嵌入。

采样

  从$q_\phi(z_{ij}|x)$采样是简单的，但是由于潜在变量是离散的，所以不能用重参数技巧，从而在采样之后执行反向传播方法。最近解决这种问题的流行方法是在一个近似离散分布的连续分布上采样，使用重参数技巧获取有偏梯度。

$$z_{ij}=softmax((h_{(i,j)}^2+g)/\tau) \tag{9}$$
以上就是这个分布，其中 $g\in\mathbb{R}^K$是一个来自于分布 $Gumbel(0,1)$的独立同分布向量， $\tau$则代表采样的平滑程度， $\tau\rightarrow 0$时分布趋于 $one-hot$形式。

解码器

  解码器的任务是预测动力系统的下一步演化结果$p_\theta(x^{t+1}|x^t,\dots,x^1,z)$，由于解码器取决于图结构$z$，所以自然可以用GNN模型作为解码器。只取决于位置和速度的物理动力系统是马尔科夫过程的$p_\theta(x^{t+1}|x^t,\dots,x^1,z)=p_\theta(x^{t+1}|x^t,z)$。为此需要使用类似于interaction networks的GNN，不过与之不同的是，这里使用单独的neural网络对每个边的类型属性进行处理。

$$v\rightarrow e:\tilde{h}_{(i,j)}^t=\sum_kz_{ij,k}\tilde{f}_e^k([x_i^t,x_j^t]) \tag{10}$$
$$e\rightarrow v:\mu_j^{t+1}=x_j^t+\tilde{f}_v(\sum_{i\ne j}\tilde{h}_{(i,j)}^t) \tag{11}$$
$$p(x_j^{t+1}|x^t,z)=\mathcal{N}(\mu_j^{t+1},\sigma^2I) \tag{12}$$
其中 $z_{ij,k}$是向量 $z_{ij}$的第 $k$个元素，$\sigma^2$是固定方差。 $z_{ij,k}$是离散 $one-hot$形式， $\tilde{h}_{(i,j)}^t$是 $\tilde{f}_e^k([x_i^t,x_j^t])$加权求和的结果。

非退化解码器

  式$(3)$中重建损失项$\sum_{t=1}^Tlog[p(x^t|x^{t-1},z)]$只涉及单步预测，而短期内，相互作用的动力系统会产生一个小的影响，这对优化来说是一个问题。例如对于物理仿真来说，就可以假设短时间内速度固定，所以忽略潜变量$z$会导致重建效果有点差。
  作者为此提出两种方法解决这个问题：首先，执行多重时间步预测，直到“退化”解码器效果很差；其次，原始模型中只用一个输入为$[x_i^t,x_j^t,z_{ij}]的$neural网络计算结果，而作者在这里使用单独的MLP网络处理每条边。这样就使模型不再忽略潜在的边属性。
  执行多重时间步预测时，用均值$\mu^t$代替$x^t$输入并循环重复执行$M$个时间步，一般为$M=10$。

$$\mu_j^2=f_{dec}(x_j^1)\\ \mu_j^{t+1}=f_{dec}(\mu_j^t)(t=2,\dots,M)\\ \mu_j^{M+2}=f_{dec}(x_j^{M+1})\\ \mu_j^{t+1}=f_{dec}(\mu_j^t)(t=M+2,\dots,2M)\\ \dots$$
在整个过程上执行反向传播， $M$步的误差累计会导致结果是次优的。

循环解码器

在许多时候马尔科夫假设并不满足，为此需要用循环解码器建模$p_\theta(x^{t+1}|x^t,\dots,x^1,z)$，解码器中添加一个GRU单元。

$$v\rightarrow e:\tilde{h}_{(i,j)}^t=\sum_kz_{ij,k}\tilde{f}_e^k([\tilde{h}_i^t,\tilde{h}_j^t]) \tag{13}$$
$$e\rightarrow v:MSG_j^t=\sum_{i\ne j}\tilde{h}_{(i,j)}^t \tag{14}$$
$$\tilde{h}_j^{t+1}=GRU([MSG_j^t,x_j^t],\tilde{h}_j^t) \tag{15}$$
$$\mu_j^{t+1}=x_j^t+f_{out}(\tilde{h}_j^{t+1}) \tag{16}$$
$$p(x^{t+1}|x^t,z)=\mathcal{N}(\mu^{t+1},\sigma^2I) \tag{17}$$
其中 $f_{out}$记为输出变换，由MLP组成。

训练

  给定样本$x$之后，先运行编码器，计算$q_\phi(z_{ij}|x)$，然后在经过重参数化后的$q_\phi(z_{ij}|x)$中采样$z_{ij}$。再运行解码器，计算$\mu^2,\dots,\mu^T$。式$(3)$有两项：重构误差和KL散度。重构误差的估计是：

$$-\sum_j\sum_{t=2}^T\frac{\parallel x_j^t-\mu_j^t\parallel^2}{2\sigma^2}+const \tag{18}$$
KL散度为：
$$\sum_{i\ne j}H(q_\phi(z_{ij}|x))+const \tag{19}$$

物理仿真实验

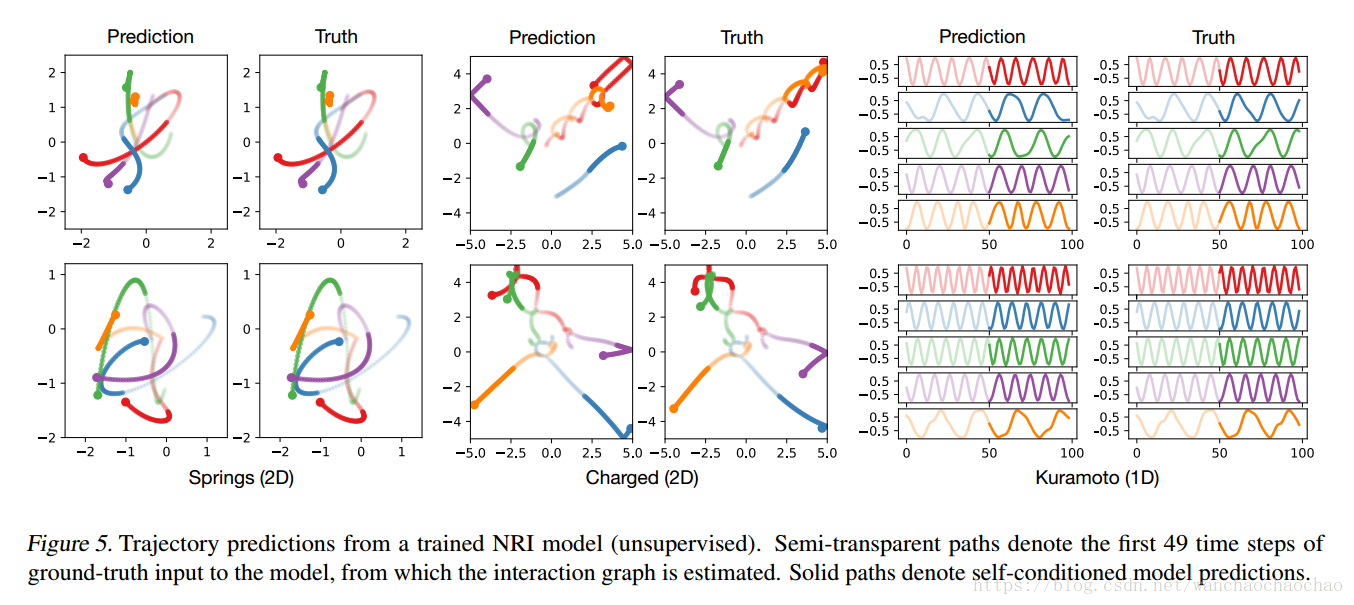
实验是基于三种系统仿真：吸引的粒子，带电粒子，姿态振荡器。这种实验配置使我们可以在相互作用关系已知的情况下，试图学习到动力系统的动态过程，这些由简单规则控制的系统，能呈现复杂动态。为此产生了5万个训练样本，1万个验证测试样本。

论文地址