写在前面:前半部分主要是讲了问题产生的原因以及问题的解决方法,后半部分讲了项目实际中需要注意哪些地方,以及浮点数这个数据类型为什么会产生这个问题,想深入了解的同学建议看完
发现问题
写这篇文章的原因是因为自己游戏中写的一句产生bug的代码,代码如下:
int currentLevel = (int)((1 - 0.8f) * 10); //猜猜得到的结果是什么?
Debug.Log("currentLevel:" + currentLevel);
我的预期这段代码应该得到的结果是2,但是当我定位到产生bug的原因在这里时,他给我的结果竟然是1! 接下来更令人匪夷所思的问题来了,同样的代码,我去掉了强转,结果却是2,代码如下:
float currentLevel = (1 - 0.8f) * 10;
Debug.Log("currentLevel:" + currentLevel); //这里得到结果2,但是上面强转又变成1了
好了,现在找到了bug产生的原因,我本来想得到的当前等级是2,但是现在给我返回的却是1,导致游戏数据异常了,那么为什么看似结果是2但是强转又变为1了呢? 接下来我就把我解决问题的思路,和产生这个问题的原因,由浅入深的讲一下。
解决问题
发现问题之后,浮现在我脑海的立马就是以下几个问题:
- 为什么强转后得到的值是1?
- 为什么直接打印的结果是2?
- 如果我想用原本的公式得到整数2该怎么做?
- 可能是浮点数的精度问题导致的?
这里我先直接给出答案,有兴趣的同学也可以继续往后看到底产生这个问题的底层原因是什么。
首先,产生这个问题的原因确实是因为浮点数的精度问题,因为下面这句代码:
//得到的结果是1.9999999999999996
float result = (1 - 0.8f) * 10;
所以1-0.8其实得到的并不是我们想要的0.2,而是0.19...无限接近0.2
解答问题1: 强转后变为1,那是因为强转的逻辑都是舍尾取整,强行转换成int类型,会把float的所有小数位直接抹除,那么因为上面的结果,导致我强转之后,结果就变成了1
解决问题2: 打印结果是2,那是因为Debug.Log()这个方法,默认是会将小数的后六位截取,然后将第第七位四舍五入到第六位,为此我做了多个测试,为了方便大家理解,我直接把测试代码以及结果放出来给大家看下。 那么,我们再来看一下最开始的那句代码,以及测试结果 这也就是解释了我们怎么打印,这个结果都是2的原因。


解答问题3: 根据需求使用函数库自带的函数,如果不是确定你的需求就是需要一个去掉所有小数部分的整数,那么请不要使用(int),我的问题是通过下面这个函数库方法解决的
//改成下面的函数
int currentLevel = (int)((1 - 0.8f) * 10);
//返回最接近该小数的整数
int currentLevel = Mathf.RoundToInt((1 - 0.8f) * 10);
解答问题4: 表面问题解决了,我们知道了浮点数的计算结果其实并不是一个精确的值,那么为什么会这样?我们实际项目中又该怎么尽量避免这种问题的发生呢?
重点!!!!
我先来说说项目中需要注意的,然后再说下浮点型这个数据类型的产生原理。 1.在做战斗计算或者浮点数的计算时,一定不要使用==来判断,自己封装一个函数来判断相等。示例代码如下:
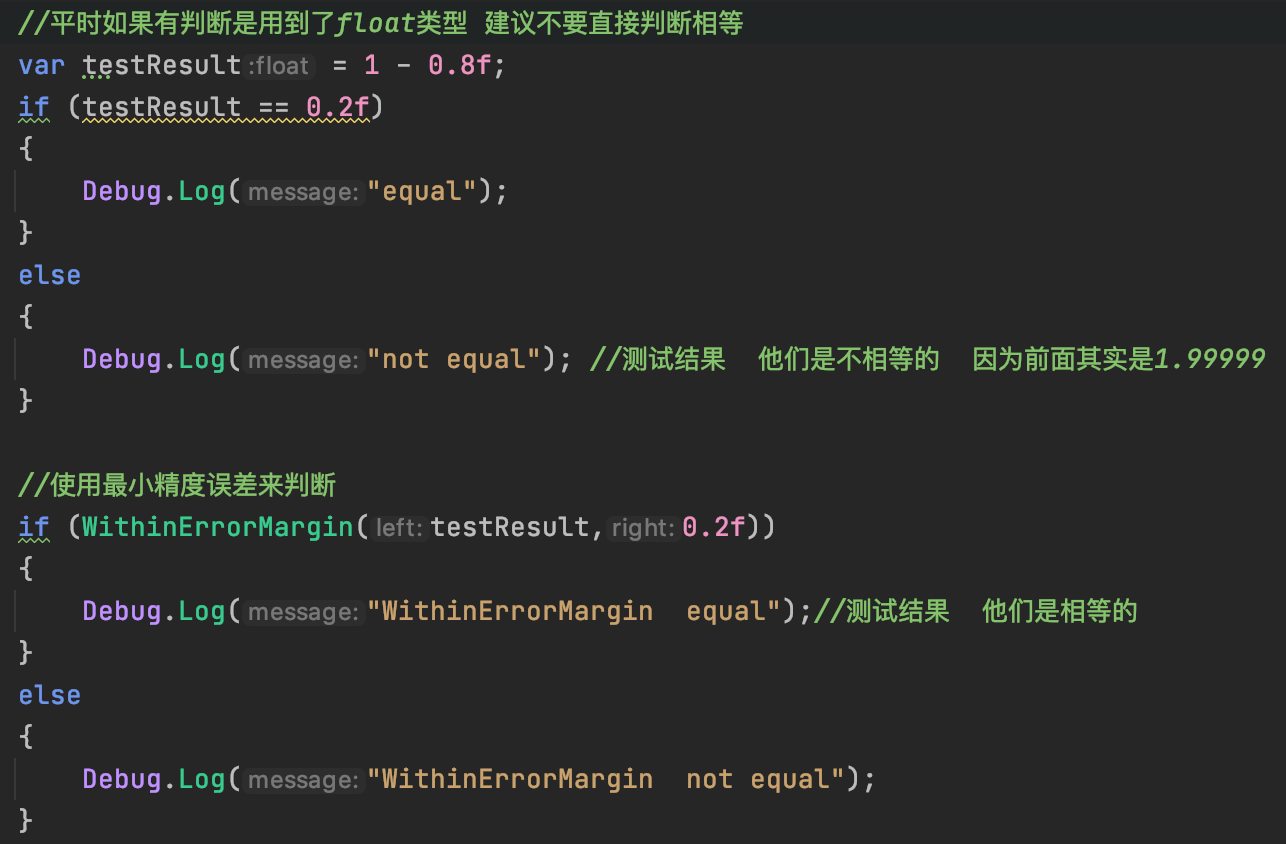

2.需要浮点数转整数的时候,根据需求选择函数库,避免强转而产生的精度丢失。 常用函数库如下

产生原理
参考资料: Computer Systems - A Programmer's Perspective 浮点数其实是分数二进制数,我们举一些比较容易理解的整数二进制的例子。 十进制数字0001,表示成二进制的话是 0001 十进制数字0002,表示成二进制的话是 0010 十进制数字0004,表示成二进制的话是 0100 十进制数字0008,表示成二进制的话是 1000 十进制数字0011, 表示成二进制的话是 1011 对数字敏感的同学应该已经看出来了,二进制数字为1的位数索引作为2的指数相加后就是十进制数字,比如二进制数1011的公式如下: 整数的二进制数,其实每一位都是作为2的次方来加权求和得到十进制数。 假设有二进制数 0000 0000 那么这8位最大能代表的整数就是255,可以自己通过上面的公式算一下。 那么浮点数,其实就是把这个二进制数的一部分作为小数部分表示了,为啥叫浮点,是因为小数点的位置是不固定的,这个是由你决定的,比如3.14和31.4,那么它表示成二进制的时候,这个小数点就在不同的位置,其实浮点数就是分数二进制数,所有的小数部分其实是有一部分二进制数的分数加起来得到的。 举个小数的例子: 5.75这个十进制浮点数,如果用二进制表示,则为 0101 . 1100 这里可以用上面的公式带入计算,不过这次,要以小数点为中界限,左边的索引从0开始向左,右边的从-1开始向右, 也就是 得到结果是 所以浮点数本质上其实在二进制中都是用分数表示的,在最后转换成我们显示的十进制时,会根据保留多少位小数的需求来决定浮点数的浮点到底在哪,而这个过程中,就会有各种精度问题了,回到问题的刚开始那里,我们使用1-0.8 其实得不到0.2也是这个精度问题导致的因为0.8f这个用二进制表示是五分之四,我们使用乘2取整法将0.8换算成二进制。 乘2取整法:即将小数部分乘以2,然后取整数部分,剩下的小数部分继续乘以2,然后取整数部分,剩下的小数部分又乘以2,一直取到小数部分为零为止。如果永远不能为零,就同十进制数的四舍五入一样,按照要求保留多少位小数时,就根据后面一位是0还是1,取舍,如果是零,舍掉,如果是1,向入一位。换句话说就是0舍1入。读数要从前面的整数读到后面的整数,下面举例: 例:将0.125换算为二进制 得出结果:将0.125换算为二进制 0000 . 0010 分析:第一步,将0.125乘以2,得0.25,则整数部分为0,小数部分为0.25; 第二步,将小数部分0.25乘以2,得0.5,则整数部分为0,小数部分为0.5; 第三步,将小数部分0.5乘以2,得1.0,则整数部分为1,小数部分为0.0; 第四步,读数,从第一位读起,读到最后一位,即为二进制数0000 . 0010。 这个例子是可以成功到零的情况,而我们的0.8,恰恰就是那个无法到0的情况。 下面我们实操一遍 第一步,将0.8乘以2,得1.6,则整数部分为1,小数部分为0.6; 第二步,将小数部分0.6乘以2,得1.2,则整数部分为1,小数部分为0.2; 第三步,将小数部分0.2乘以2,得0.4,则整数部分为0,小数部分为0.4; 第四步,将小数部分0.4乘以2,得0.8,则整数部分为0,小数部分为0.8;//从这里开始进入无限循环 。。。。。。 第N步,读数,从第一位读起,读到最后一位,即为 0000 . 11001100110011001100..... 所以零点八这个十进制数,最终变成二进制分位数必然是会丢失精度的,因为二进制分位数只能无限趋近与0.8,并不能完全等于0.8,也就导致最终计算的时候1-0.8 = 1.9999999999 很有可能就是某次循环的0舍1入导致0.8最终计算的时候比0.8稍微大了那么一丢丢,所以得到的结果就不是0.2了,而是比0.2小了那么一丢丢的0.1999999999,至此,我们的浮点数之旅就告一段落了.......
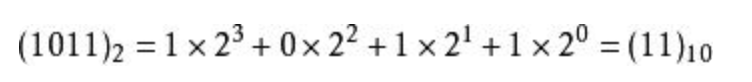
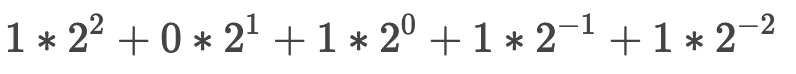
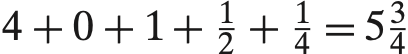




 本文通过一个游戏代码bug引出浮点数精度问题,详细解释了浮点数计算时出现误差的原因,并提供了解决方案。在项目实践中,要注意避免使用`==`进行浮点数比较,以及在转换整数时选择合适的函数,如Unity中的`Mathf.RoundToInt()`。此外,还介绍了浮点数的二进制表示和乘2取整法,帮助理解浮点数精度丢失的原理。
本文通过一个游戏代码bug引出浮点数精度问题,详细解释了浮点数计算时出现误差的原因,并提供了解决方案。在项目实践中,要注意避免使用`==`进行浮点数比较,以及在转换整数时选择合适的函数,如Unity中的`Mathf.RoundToInt()`。此外,还介绍了浮点数的二进制表示和乘2取整法,帮助理解浮点数精度丢失的原理。
















 458
458

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








