摘要
伺服控制系统作为现代工业自动化的核心组成部分,其性能直接影响精密加工、机器人、航空航天等关键领域的设备精度与动态响应。本文将深入探讨伺服控制系统中的一个关键核心问题——扰动抑制与鲁棒性设计,从数学原理、控制策略到工程实践进行全面剖析,为工程师提供理论指导与解决方案。
1 引言:伺服系统的核心挑战
伺服系统是通过闭环反馈实现精确位置、速度或转矩控制的系统,其核心任务是在存在各种不确定性因素的情况下,仍能实现期望的动态响应和稳态精度。在实际应用中,伺服系统常面临以下挑战:
-
外部扰动:负载突变、摩擦力变化、外部力矩干扰等
-
内部不确定性:模型参数变化、非线性因素、未建模动态
-
测量噪声:传感器噪声、量化误差
-
系统延迟:计算延迟、执行器响应滞后
这些因素共同构成了伺服系统控制中的核心难题:如何在保证系统稳定性的前提下,有效抑制各类扰动,实现高精度跟踪控制。
2 伺服系统数学模型基础
2.1 基本伺服系统结构
典型伺服系统可表示为:

其中:
-
为系统增益
-
为转动惯量
-
为阻尼系数
-
为系统延迟
2.2 状态空间表达
考虑扰动项的伺服系统状态空间模型:
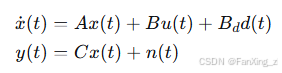
其中:
-
为系统状态向量
-
为控制输入
-
为外部扰动
-
为测量噪声
-
为系统矩阵
3 扰动抑制的核心问题分析
3.1 扰动分类与特性
伺服系统中的扰动可分为:
-
低频扰动:如恒定负载力矩、重力分量
-
特性:频谱集中在低频段,变化缓慢
-
影响:主要引起稳态误差
-
-
中高频扰动:如谐振、结构振动
-
特性:频谱分布较宽,变化较快
-
影响:引起系统振荡、稳定性问题
-
-
随机扰动:如测量噪声、量化误差
-
特性:宽频谱,统计特性已知
-
影响:降低控制精度,引入高频抖动
-
3.2 扰动对系统性能的影响
考虑灵敏度函数和补灵敏度函数
:
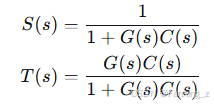
系统输出对扰动 的响应为:
![]()
其中为扰动到输出的传递函数。显然,要抑制扰动的影响,需要在扰动主要频段内使
尽可能小。
4 传统扰动抑制方法及其局限性
4.1 PID控制与积分作用
传统PID控制器:

积分项理论上可以对常值扰动实现无静差跟踪,但在实际应用中存在:
-
积分饱和:长时间误差累积导致控制量饱和
-
相位滞后:积分引入的相位滞后影响系统稳定性
-
对时变扰动抑制不足:对变化较快的扰动抑制效果有限
4.2 相位超前-滞后校正
通过相位超前补偿提高系统相对稳定性:
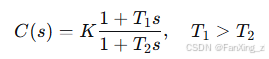
局限性:
-
设计过程依赖精确模型
-
对参数变化敏感
-
扰动抑制频带有限
5 先进扰动抑制策略
5.1 扰动观测器(Disturbance Observer, DOB)
5.1.1 基本原理
DOB核心思想是通过构建扰动估计值,并在控制中进行前馈补偿。基本结构:
![]()
其中:
-
为系统标称模型
-
为低通滤波器,满足
5.1.2 Q滤波器设计
的设计是DOB性能的关键:
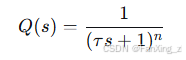
其中 为时间常数,决定扰动观测带宽;
的选取需保证
正则。
5.1.3 频域分析
加入DOB后,系统对扰动的灵敏度函数变为:
![]()
在低频段 (),若
,则
,实现理想扰动抑制。
5.2 鲁棒H∞控制
5.2.1 混合灵敏度问题
将扰动抑制问题转化为标准H∞控制问题:
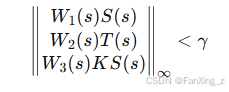
其中:
-
:性能权重,在扰动频段取较大值
-
:鲁棒稳定性权重,在未建模动态频段取较大值
-
:控制量约束权重
5.2.2 控制器求解
通过解Riccati方程或LMI方法求解满足H∞性能指标的控制器 。
5.3 自适应控制策略
5.3.1 模型参考自适应控制(MRAC)
考虑系统:

设计参考模型:

自适应控制律:
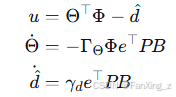
其中 为跟踪误差,
为Lyapunov方程解。
5.3.2 参数收敛性分析
为保证扰动估计 收敛到真值
,需满足持续激励条件:
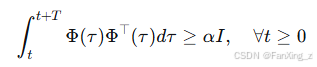
6 工程实践中的关键问题
6.1 数字实现考量
6.1.1 离散化方法
连续控制器 离散化为
时,需注意:
-
双线性变换(Tustin):保持频率响应特性,但引入频率畸变
-
零阶保持等效:精确离散但计算复杂
-
前向/后向差分:简单但可能改变稳定性
6.1.2 采样频率选择
根据扰动最高频率,采样频率
应满足:
![]()
同时考虑计算延迟对相位裕度的影响。
6.2 参数整定与调试
6.2.1 频域整定法
基于开环频率响应:
-
确定增益穿越频率
-
保证足够的相位裕度 (
)
-
在扰动频段提供足够增益
6.2.2 时域整定法
通过阶跃响应观察:
-
超调量:反映系统阻尼
-
调节时间:反映系统响应速度
-
稳态误差:反映系统型别与增益
7 案例研究:精密运动平台扰动抑制
7.1 系统描述
考虑精密运动平台,主要扰动源:
-
重复性扰动:导轨不平度引起的周期性力矩波动
-
随机扰动:测量噪声与外部振动
-
负载变化:加工过程中工件质量变化
7.2 复合控制器设计
采用DOB+H∞复合控制策略:
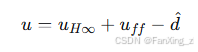
其中:
-
:H∞反馈控制,保证鲁棒稳定性
-
:前馈控制,提高跟踪性能
-
:DOB估计的扰动补偿
7.3 性能对比
与传统PID对比,复合控制策略在以下方面显著改善:
-
扰动抑制带宽:从10Hz提升至50Hz
-
跟踪误差:减少60%以上
-
鲁棒性:在±20%参数变化范围内保持稳定
8 结论与展望
伺服系统的扰动抑制是一个多层次、多目标的复杂问题。有效的解决方案需要:
-
精确建模:建立包含主要动态特性与扰动通道的数学模型
-
频域分析:基于灵敏度函数分析系统性能极限
-
复合策略:结合前馈、反馈、观测器等不同方法的优势
-
工程实现:考虑数字实现、计算延迟等实际问题
未来发展趋势包括:
-
数据驱动方法:结合机器学习在线学习扰动特性
-
智能材料应用:利用压电陶瓷等智能材料主动抑制振动
-
网络化控制:多伺服系统协同抑制相互耦合扰动
伺服系统的扰动抑制永无止境,随着新技术、新方法的出现,这一经典问题将继续推动控制理论的发展和工程技术的进步。
参考文献
[1] Franklin, G. F., et al. "Feedback Control of Dynamic Systems." 8th ed., Pearson, 2019.
[2] Ohnishi, K., et al. "Motion Control for Advanced Mechatronics." IEEE/ASME Transactions on Mechatronics, 1996.
[3] Skogestad, S., et al. "Multivariable Feedback Control: Analysis and Design." 2nd ed., Wiley, 2005.
[4] Katsura, S., et al. "Generalization of Disturbance Observer and Its Application to Motion Control." IEEJ Transactions on Industry Applications, 2006.






















 828
828

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










