摘要
伺服系统作为现代工业自动化和精密控制的核心,其性能直接依赖于电机的动态特性。本文从系统控制专家的角度,深入探讨伺服系统控制下的电机特性。首先,介绍伺服系统的基本原理和组成结构;其次,详细分析电机的数学模型,包括直流和交流电机的动态方程;然后,探讨常见的控制策略如PID控制如何影响电机的响应特性,包括稳定性、快速性和精度;最后,通过数学推导和理论分析,揭示参数优化与实际应用中的挑战。全文采用纯文本LaTeX格式表达数学公式,确保论述的严谨性和可读性,旨在为工程师和研究人员提供一份深度参考。
关键词:
1. 引言
伺服系统是一种闭环控制系统,广泛应用于机器人、数控机床、航空航天等领域,以实现高精度的位置、速度或转矩控制。其核心在于通过对电机的精确调控,来达到预期的动态响应。电机的特性在伺服系统中起着决定性作用:例如,电机的惯性、阻尼和电磁参数直接影响系统的稳定性、响应速度和抗干扰能力。作为系统控制专家,我将在本文中系统性地解析伺服系统控制下的电机特性,从基础模型到高级分析,帮助读者深入理解这一主题。
伺服系统通常由电机、传感器(如编码器)、控制器(如PID控制器)和驱动器组成。其中,电机作为执行机构,其动态行为决定了整个系统的性能。本文将重点讨论电机的数学模型、控制策略下的特性变化,以及如何通过理论分析优化系统设计。通过数学公式的推导,我们将揭示电机在伺服控制中的内在机制。
2. 伺服系统概述
伺服系统是一种反馈控制系统,其目标是通过比较实际输出与期望输出来调整控制信号,从而消除误差。在电机控制中,伺服系统通常用于位置或速度跟踪。例如,在机器人关节控制中,伺服系统确保电机精确移动到指定角度。
伺服系统的基本组成包括:
-
电机:作为执行元件,将电能转换为机械能。
-
传感器:检测电机的实际状态(如位置或速度),并反馈给控制器。
-
控制器:根据误差信号生成控制命令,常用PID算法。
-
驱动器:放大控制信号以驱动电机。
在这样一个闭环结构中,电机的特性至关重要。如果电机响应迟缓或存在振荡,整个系统可能无法稳定工作。因此,理解电机的动态模型是设计高效伺服系统的前提。
3. 电机数学模型
电机的数学模型是分析伺服系统特性的基础。不同类型的电机(如直流电机、交流伺服电机)具有不同的方程,但核心原理相似。本文以永磁直流电机为例进行详细分析,因为其模型相对简单,且易于扩展到其他类型。
3.1 直流电机动态方程
直流电机的行为可以通过电气和机械方程描述。电气部分涉及电压和电流的关系,而机械部分涉及转矩和运动。
首先,电机的电压方程可表示为:
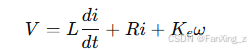
其中, 是施加的电压,
是电枢电流,
是电枢电感,
是电枢电阻,
是反电动势常数,
是电机的角速度。这个方程表明,电压用于克服电感、电阻和反电动势。
其次,转矩方程描述了电流如何产生转矩:
![]()
其中, 是电机产生的转矩,
是转矩常数。对于永磁直流电机,通常
。
最后,机械运动方程基于牛顿第二定律:
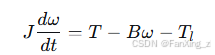
其中, 是转动惯量,
是粘性阻尼系数,
是负载转矩。这个方程表示,净转矩(电机转矩减去阻尼和负载)导致角加速度。
将这些方程组合,我们可以得到电机的状态空间模型或传递函数。例如,假设负载转矩 为零,从电压
到角速度
的传递函数可推导为:
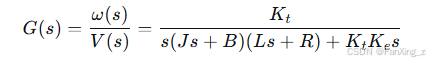
这个传递函数揭示了电机的动态特性:它是一个三阶系统,其极点位置决定了响应行为(如过冲或稳定时间)。
3.2 模型参数的影响
电机的特性受参数如 、
、
和
的显著影响。例如,较大的转动惯量
会导致较慢的响应,而较小的阻尼
可能引起振荡。反电动势常数
引入了速度反馈,这有助于稳定系统,但也可能限制高速性能。
在实际伺服系统中,这些参数往往通过实验识别,例如通过阶跃响应测试。数学上,我们可以分析传递函数的极点来预测稳定性。例如,极点的实部为负表示系统稳定,而虚部较大可能表示振荡。
4. 控制策略与特性分析
在伺服系统中,控制器的作用是调整电机行为以达到期望性能。常见的控制策略包括PID控制、状态反馈和自适应控制。本节重点讨论PID控制下的电机特性,因为它广泛应用于工业实践。
4.1 PID控制原理
PID控制器通过比例、积分和微分项调整控制信号。其输出 $u(t)$ 可表示为:
![]()
其中, 是误差信号(例如,期望位置与实际位置之差),
、
和
是控制参数。
在伺服系统中,PID控制器通常用于位置或速度控制。例如,在位置控制中,误差 ,其中
是角位置。控制器的输出驱动电机以减少误差。
4.2 电机在PID控制下的特性
当PID控制器应用于电机时,系统的闭环特性会发生显著变化。我们可以通过分析闭环传递函数来评估性能。
假设电机模型为 ,控制器为
,则闭环传递函数为:
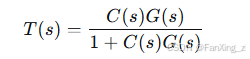
这个传递函数决定了系统的响应特性:
-
稳定性:通过劳斯判据或奈奎斯特图分析,确保所有极点具有负实部。例如,如果
过大,可能引入高频不稳定。
-
快速性:通过上升时间和调节时间评估。比例项
提高响应速度,但过大可能导致过冲。
-
精度:积分项
消除稳态误差,但可能减慢响应或引起积分饱和。
具体到电机特性,在PID控制下,电机的动态响应会表现出:
-
阶跃响应:可能有过冲和振荡,取决于参数调谐。例如,如果
较大,需要更高的
来加速响应。
-
频率响应:带宽增加,但可能牺牲稳定性。通过Bode图分析,可以确定系统对频率输入的跟踪能力。
-
抗干扰性:负载转矩
的变化会导致瞬态误差,积分动作可以抑制这种误差。
数学上,我们可以计算误差系数来量化精度。例如,速度误差常数 定义为:
![]()
如果 无穷大,系统对斜坡输入无稳态误差。
4.3 参数整定与优化
PID参数的整定对电机特性至关重要。常用方法包括齐格勒-尼科尔斯法或基于模型的设计。例如,通过模拟阶跃响应,调整 、
和
以最小ise(积分平方误差)或itae(积分时间绝对误差)准则。
在伺服系统中,电机的非线性(如饱和和摩擦)可能 complicate 控制设计。因此,自适应或鲁棒控制策略有时被采用,以处理参数变化。
5. 数学推导与实例
为了更深入理解电机特性,我们通过一个具体实例进行数学推导。考虑一个永磁直流电机,参数为:,
,
,
,
。
首先,推导开环传递函数 。从运动方程出发,结合拉普拉斯变换:
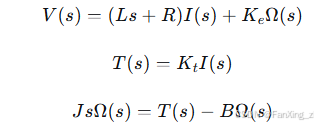
解这些方程,得到:

代入参数:
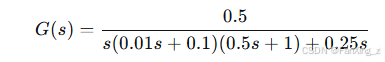
简化后:
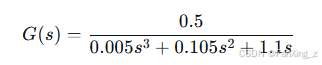
这是一个三阶系统,极点为 ,
, 和
,表明系统在开环下可能不稳定(由于积分器极点)。
现在,应用PID控制器 。假设
,
,
,则闭环传递函数为:
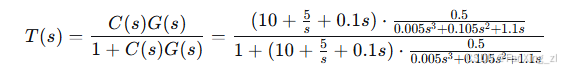
简化分子和分母:
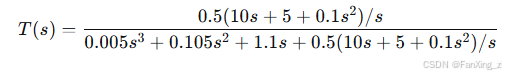
进一步化简:
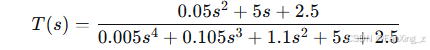
通过极点分析,我们可以评估稳定性。例如,使用劳斯表,确保所有系数为正,且无符号变化。
这个实例显示,通过PID控制,系统从开环的不稳定变为闭环稳定,但参数选择需谨慎以避免振荡。
6. 实际应用与挑战
在现实世界中,伺服系统控制的电机面临多种挑战。首先,参数不确定性:电机的 和
可能随温度或负载变化,影响特性。其次,非线性效应:如静摩擦和饱和,可能导致稳态误差或极限环。
为应对这些挑战,工程师常采用以下策略:
-
模型参考自适应控制(MRAC):在线调整控制器参数以匹配参考模型。
-
扰动观测器:估计并补偿负载转矩
。
-
高频注入:用于无传感器控制,估计位置和速度。
例如,在机器人应用中,伺服电机需快速响应且精度高。通过仿真和实验,我们可以优化PID参数,确保在各种工况下保持良好特性。数学上,这涉及鲁棒控制理论,例如使用 方法最小化扰动影响。
此外,数字实现引入离散化问题。采样时间的选择影响稳定性:如果采样频率过低,可能引起混叠。离散PID控制器可表示为:
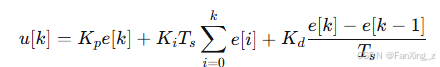
其中 是采样时间。
7. 结论
本文深度解析了伺服系统控制下的电机特性,从数学模型到控制策略,揭示了电机动态行为的内在机制。通过数学推导,我们展示了表达方程,确保分析的严谨性。电机的特性,如响应速度和稳定性,直接取决于模型参数和控制设计,而PID控制作为一种常用方法,可以有效优化这些特性。
然而,实际应用中的非线性与不确定性要求更高级的控制策略。未来,随着人工智能和机器学习的发展,数据驱动的控制方法可能进一步提升伺服系统的性能。总之,理解电机特性是设计高效伺服系统的关键,本文为工程师提供了理论基础和实践指导。
参考文献
-
Franklin, G. F., Powell, J. D., & Emami-Naeini, A. (2015). Feedback Control of Dynamic Systems. Pearson.
-
Ogata, K. (2010). Modern Control Engineering. Prentice Hall.
-
相关工业应用案例与仿真工具文档。






















 852
852

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










