注:本文为 “旋转变换 · Gimbal Lock” 相关合辑。
图片清晰度受引文原图所限。
略作重排,如有内容异常,请看原文。
欧拉角之万向锁问题(Gimbal Lock)
Jay_z 在造梦 原创于 2021-05-07 11:31:21 发布
前言
在学习《视觉 SLAM 十四讲》时,曾对欧拉角的万向锁问题产生困惑。近期重新梳理相关资料,结合多篇技术博文、动画演示及数学推导,发现多数解释未清晰阐明坐标轴平行的成因与本质逻辑。本文将基于刚体运动学原理、坐标系变换规则及数学约束条件,系统拆解欧拉角与万向锁的内在关联,力求准确呈现现象本质与解决思路,疏漏之处恳请指正。
一、欧拉角的定义、分类与特性
1. 欧拉角的定义
欧拉角是三维空间中描述刚体旋转的经典数学工具,其逻辑是将任意复杂旋转分解为三次绕坐标轴的有序旋转。由于旋转轴选择(世界坐标系或物体坐标系)与旋转顺序的灵活性,欧拉角存在多种定义方式,常见旋转顺序包括
Z
Y
X
ZYX
ZYX、
X
Y
Z
XYZ
XYZ、
Z
Y
Z
ZYZ
ZYZ 等,且满足 “刚体任意旋转均可分解为三次绕轴旋转,但分解方式不唯一” 的特性。例如:设绕
y
y
y 轴旋转为 heading、绕
x
x
x 轴旋转为 pitch、绕
z
z
z 轴旋转为 bank,则 “先 heading
4
5
∘
45^\circ
45∘ 再 pitch
9
0
∘
90^\circ
90∘” 与 “先 pitch
9
0
∘
90^\circ
90∘ 再 bank
4
5
∘
45^\circ
45∘” 的旋转结果完全等价。
2. 欧拉角的分类
根据旋转轴是否随刚体运动,欧拉角可分为两类:
- 静态欧拉角:绕世界坐标系(固定不变的笛卡尔坐标系)的坐标轴旋转,旋转过程中坐标轴方向保持静止,仅与刚体初始姿态和旋转角度相关。
- 动态欧拉角:绕物体坐标系(与刚体固连、随刚体同步旋转的内部坐标系)的坐标轴旋转,后一轴的旋转方向依赖于前一轴的旋转结果,旋转顺序对最终姿态影响显著。
在工程应用中,动态欧拉角因更贴合刚体自身运动特性,应用场景更为广泛(如机器人导航、飞行器控制、SLAM 姿态估计等)。
3. 欧拉角的优缺点
优点
- 直观易懂,符合人类对旋转运动的认知习惯,可根据需求灵活定义旋转规则;
- 表达简洁,仅需三个角度参数(如 x , y , z x, y, z x,y,z 轴旋转角)即可描述姿态,存储空间占用少;
- 任意三个角度组合均为合法表达,无参数取值范围外的无效组合。
缺点
- 姿态表达方式不唯一:同一刚体姿态可对应多组不同的欧拉角,易导致数据歧义;
- 插值计算困难:直接对两组欧拉角的角度参数进行线性插值,无法获得平滑的三维旋转路径,易出现姿态跳变。
二、万向锁问题的预备知识
1. Gimbal(平衡架)的结构与功能

平衡架(Gimbal)是一种多轴枢转支撑装置,允许被支撑物体绕指定轴线旋转。一组由三个正交枢轴依次嵌套的万向架,可使最内层的物体保持独立于支撑结构的姿态稳定性 —— 即使支撑结构发生俯仰、滚动等运动,内层物体仍能维持预设姿态。例如:船舶上的陀螺仪、指南针、航海炉具等设备,均通过万向架实现水平姿态保持,抵消船体颠簸带来的姿态扰动(参考维基百科定义)。
2. 旋转运动的专业术语
在飞行器、机器人等领域,三维旋转运动存在标准化术语描述,分为两组:
(1)Roll-Pitch-Yaw 术语体系
该体系以物体自身坐标系为参考,对应绕
x
,
y
,
z
x, y, z
x,y,z 轴的旋转,示意图如下:

- Pitch(俯仰):绕机身右向轴(对应欧拉角 x x x 轴)的旋转;
- Yaw(偏航):绕机头上方轴(对应欧拉角 y y y 轴)的旋转;
- Roll(桶滚):绕机头前方轴(对应欧拉角 z z z 轴)的旋转。
(2)Heading-Pitch-Bank 术语体系
该体系用于描述物体坐标系到惯性坐标系的旋转映射,其中:
Yaw与Heading等价,均指偏航运动;Roll与Bank等价,均指桶滚运动;
其特性与欧拉角旋转分解一致,例如 “先heading4 5 ∘ 45^\circ 45∘ 再pitch9 0 ∘ 90^\circ 90∘” 与 “先pitch9 0 ∘ 90^\circ 90∘ 再bank4 5 ∘ 45^\circ 45∘” 等价,此特性与万向锁现象直接相关。
补充说明:惯性坐标系
惯性坐标系是物体坐标系与世界坐标系的过渡媒介,其原点与物体坐标系重合,坐标轴方向与世界坐标系保持一致,用于简化两类坐标系间的变换计算。
三、万向锁问题的现象、成因与数学解析
1. 万向锁的现象本质
万向锁(Gimbal Lock)源于平衡架的轴系嵌套特性,本质是刚体旋转过程中丢失一个自由度的奇异性问题。当第二次旋转角度(如 P i t c h = ± 9 0 ∘ Pitch = \pm90^\circ Pitch=±90∘)满足特定条件时,第三次旋转的效果与第一次旋转完全重合,导致刚体无法实现三维空间中的任意姿态调整,仅能在二维平面内运动。
现象演示(以 Y X Z YXZ YXZ 旋转顺序为例)
通过嵌套式平衡架(RGB 三色环分别对应 X , Y , Z X, Y, Z X,Y,Z 轴)演示万向锁过程,平衡架的轴系存在嵌套父子关系:外层轴旋转会带动所有内层轴同步改变方向,中层轴旋转仅带动内层轴方向改变,内层轴旋转不影响外层轴。具体步骤如下:
- 初始状态:三个轴系相互正交,无任何旋转;
- 第一次旋转(绕 Y Y Y 轴):任意角度旋转,轴系保持正交,无异常;
- 第二次旋转(绕 X X X 轴):当旋转角度为 9 0 ∘ 90^\circ 90∘ 时, Z Z Z 轴(内层轴)与 Y Y Y 轴(外层轴)的方向完全平行,轴系从三维正交退化为二维正交;
- 第三次旋转(绕 Z Z Z 轴):旋转效果与绕 Y Y Y 轴旋转完全一致,刚体无法实现绕垂直于二维平面方向的旋转,即丢失一个自由度。
相关状态示意图如下:
- 正常旋转状态(
P
i
t
c
h
≠
±
9
0
∘
Pitch \neq \pm90^\circ
Pitch=±90∘):

- 万向锁触发状态(
P
i
t
c
h
=
9
0
∘
Pitch = 90^\circ
Pitch=90∘,轴系平行):

万向锁的触发场景
所有欧拉角旋转顺序(共 6 种基础顺序: X Y Z , X Z Y , Y X Z , Y Z X , Z X Y , Z Y X XYZ, XZY, YXZ, YZX, ZXY, ZYX XYZ,XZY,YXZ,YZX,ZXY,ZYX)均可能触发万向锁,且触发条件均为第二次旋转角度达到 ± 9 0 ∘ \pm90^\circ ±90∘,示意图如下:

2. 万向锁的成因解析
(1)空间运动视角:坐标系与轴系耦合
万向锁的成因是旋转轴系的耦合重合,关键在于明确旋转所依赖的坐标系:
- 若旋转顺序为 Y X Z YXZ YXZ,绕 Y Y Y 轴的旋转基于惯性坐标系(固定不变),绕 X X X 轴和 Z Z Z 轴的旋转基于物体坐标系(随刚体运动);
- 当绕 X X X 轴旋转 9 0 ∘ 90^\circ 90∘ 时,物体坐标系的 Z Z Z 轴被旋转至与惯性坐标系的 Y Y Y 轴平行,此时 “绕物体坐标系 Z Z Z 轴旋转” 与 “绕惯性坐标系 Y Y Y 轴旋转” 的运动效果完全一致,导致两个旋转自由度相互抵消,仅剩余一个二维旋转自由度。
即使所有旋转均基于惯性坐标系,仍会因轴系方向重合导致万向锁,本质是欧拉角 “三次有序旋转” 的定义逻辑本身存在缺陷 —— 三次旋转无法完全独立,必然存在轴系耦合的可能性。
(2)数学视角:欧拉角微分方程的约束
欧拉角的姿态描述可通过微分方程表征,其约束条件如下:

由方程可知,当 P i t c h = ± 9 0 ∘ Pitch = \pm90^\circ Pitch=±90∘ 时, cos ( P i t c h ) = 0 \cos (Pitch) = 0 cos(Pitch)=0,方程系数矩阵出现奇异性,导致角速度与欧拉角变化率之间的映射关系失效,无法通过三次旋转实现任意姿态的连续变换。
(3)不同姿态表达方式的对比
三维姿态描述的三种方式(欧拉角、四元数、旋转矩阵)在万向锁问题上的表现差异如下:
| 表达方式 | 万向锁问题 | 特性 | 适用场景 |
|---|---|---|---|
| 欧拉角 | 存在( P i t c h = ± 9 0 ∘ Pitch = \pm90^\circ Pitch=±90∘ 触发) | 直观易懂、存储量小;插值不平滑、多义性 | 人机交互、姿态可视化 |
| 四元数 | 不存在 | 插值平滑(球面插值)、存储量中等;理解难度高 | 姿态插值、连续运动控制 |
| 旋转矩阵 | 不存在 | 计算机运算友好、无多义性;存储冗余、插值困难 | 正逆运动学计算、坐标系变换 |
工程应用中通常采用 “人机交互用欧拉角、插值计算用四元数、运动学运算用旋转矩阵” 的组合方案,规避单一表达方式的缺陷。
3. 万向锁问题的规避策略
(1)角度范围约束
将欧拉角的 P i t c h Pitch Pitch 取值范围限制在 ( − π / 2 , π / 2 ) (-\pi/2, \pi/2) (−π/2,π/2) 内,避免触发 P i t c h = ± 9 0 ∘ Pitch = \pm90^\circ Pitch=±90∘ 的临界状态;或根据具体应用场景,设计无需 P i t c h Pitch Pitch 旋转至 ± 9 0 ∘ \pm90^\circ ±90∘ 的运动逻辑,从需求层面规避万向锁。
(2)更换姿态表达方式
在 SLAM 系统、机器人导航等需要连续姿态估计与平滑插值的场景中,优先采用四元数或旋转矩阵描述姿态,彻底避免万向锁问题。其中四元数因存储量小、插值性能优异,是动态姿态控制的首选方案。
四、Reference
博文
- unity 旋转欧拉角 万向锁 解释_unity 解万向锁-优快云博客
https://blog.youkuaiyun.com/fengya1/article/details/50721768 - [Unity] Unity 3D 中的旋转_unity 旋转向量-优快云博客
https://blog.youkuaiyun.com/icevmj/article/details/80280929 - 欧拉角详解-优快云博客
https://blog.youkuaiyun.com/caimouse/article/details/55259669 - 欧拉角死锁_刚体运动学最通俗易懂的理解万向节死锁-优快云博客
https://blog.youkuaiyun.com/weixin_39904268/article/details/112417665
视频
图源
上述博文、视频截图及维基百科
关于万向锁(Gimbal Lock)问题的理解及解决
罗伯特祥 原创于 2023-06-21 09:35:55
1. Gimbal Lock 的理解
万向锁(Gimbal Lock):当以 ± 9 0 ∘ \pm 90^\circ ±90∘ 作为俯仰角(pitch)时,第一次旋转与第三次旋转的作用效果等价,导致整个旋转表示系统被限制为仅能绕竖直轴旋转,丢失一个表示维度。
万向锁问题仅存在于动态欧拉角中,静态欧拉角无此现象。
- 静态欧拉角:绕世界坐标系的三个轴进行旋转,旋转过程中坐标轴保持固定不变,各变换顺序对应的旋转矩阵采用左乘方式。
- 动态欧拉角:绕物体坐标系的三个轴进行旋转,旋转过程中坐标轴随物体同步转动,各变换顺序对应的旋转矩阵采用右乘方式。
- 内旋(Intrinsic rotations):绕运动轴(物体坐标系轴)的旋转。
- 外旋(Extrinsic rotations):绕固定轴(世界坐标系轴)的旋转。

无论采用何种欧拉角定义,只要中间步骤的旋转角度为 9 0 ∘ 90^\circ 90∘,就会触发万向锁问题。
案例 1
典型的万向锁问题可描述为:先绕航向角(heading)旋转 4 5 ∘ 45^\circ 45∘ 再绕俯仰角(pitch)旋转 9 0 ∘ 90^\circ 90∘,与先绕俯仰角(pitch)旋转 9 0 ∘ 90^\circ 90∘ 再绕横滚角(bank)旋转 4 5 ∘ 45^\circ 45∘ 的效果完全等价。当俯仰角(pitch)取 ± 9 0 ∘ \pm 90^\circ ±90∘ 时,第一次旋转与第三次旋转的旋转轴趋于重合,导致系统仅能绕竖直轴旋转,丢失一个表示维度。这种因第二次旋转角度为 ± 9 0 ∘ \pm 90^\circ ±90∘ 而使第一次与第三次旋转轴相同的现象,称为万向锁。


案例 2
定义手机的物体坐标系: z z z 轴与手机屏幕垂直且指向上方(手机平放于桌面), x x x 轴沿手机较短边方向, y y y 轴沿手机较长边方向(由手机尾部指向头部),坐标系原点为手机左下角顶点,旋转顺序为 z → y → x z \to y \to x z→y→x。
操作步骤:先绕 z z z 轴旋转任意角度( x x x 轴与 y y y 轴随手机同步旋转),再绕 y y y 轴旋转 9 0 ∘ 90^\circ 90∘,最后绕 x x x 轴旋转任意角度。多次实验后可发现: z z z 轴始终保持水平状态,手机无法绕竖直方向立起,其旋转形成的三维空间被限制在固定平面内。原本预期手机可指向三维空间任意方向,但实际仅能指向水平面上的特定方向,此现象即为万向锁。
若绕 y y y 轴的旋转角度不等于 9 0 ∘ 90^\circ 90∘(如 1 ∘ 1^\circ 1∘ 或 8 9 ∘ 89^\circ 89∘),通过合理选择绕 x x x 轴与 z z z 轴的旋转角度,可使手机指向三维空间任意方向,旋转产生的三维空间无重叠,不会出现万向锁现象。
2. 解决方案
(1)使用四元数解决
将欧拉角转换为四元数表示,对四元数执行球面线性插值(slerp)运算,再将插值后的四元数序列转换为对应的欧拉角,最终作用于目标物体。
该方法的不足是需占用一定内存资源,但目标物体可实现任意角度旋转,运动灵活性较高。
(2)采用四元数的原因
- 规避万向锁问题:四元数通过四维空间表示三维旋转,不存在旋转轴重合导致的维度丢失问题。
- 插值平滑性:直接对欧拉角(RPY)进行插值易出现跳跃现象,四元数的球面线性插值可保证旋转过程连续平滑。
- 计算效率:四元数表示旋转时所需的运算次数少于欧拉角,尤其适用于实时控制系统。
- 插值适配性:四元数的数学特性使其天然适合旋转插值运算,其中球面线性插值(slerp)应用最为广泛。
注意事项:使用四元数插值时,需对插值结果进行归一化(规范化 / 规格化)处理,否则四元数的单位长度特性会被破坏,导致旋转精度下降。
3. 欧拉角与四元数的对应关系
| 欧拉角(pitch, yaw, roll) | ←→ | 四元数(第一个值为虚部,后三个值为实部) |
|---|---|---|
| ( 0. 0 ∘ , 0. 0 ∘ , 0. 0 ∘ ) (0.0^\circ, 0.0^\circ, 0.0^\circ) (0.0∘,0.0∘,0.0∘) | ←→ | ( 1.000000 , 0.000000 , 0.000000 , 0.000000 ) (1.000000, 0.000000, 0.000000, 0.000000) (1.000000,0.000000,0.000000,0.000000) |
| ( 90. 0 ∘ , 0. 0 ∘ , 0. 0 ∘ ) (90.0^\circ, 0.0^\circ, 0.0^\circ) (90.0∘,0.0∘,0.0∘) | ←→ | ( 0.707107 , 0.707107 , 0.000000 , 0.000000 ) (0.707107, 0.707107, 0.000000, 0.000000) (0.707107,0.707107,0.000000,0.000000) |
| ( 0. 0 ∘ , 90. 0 ∘ , 0. 0 ∘ ) (0.0^\circ, 90.0^\circ, 0.0^\circ) (0.0∘,90.0∘,0.0∘) | ←→ | ( 0.707107 , 0.000000 , 0.707107 , 0.000000 ) (0.707107, 0.000000, 0.707107, 0.000000) (0.707107,0.000000,0.707107,0.000000) |
| ( 0. 0 ∘ , 0. 0 ∘ , 90. 0 ∘ ) (0.0^\circ, 0.0^\circ, 90.0^\circ) (0.0∘,0.0∘,90.0∘) | ←→ | ( 0.707107 , 0.000000 , 0.000000 , 0.707107 ) (0.707107, 0.000000, 0.000000, 0.707107) (0.707107,0.000000,0.000000,0.707107) |
4. 使用四元数的注意事项
- 避免将绕 RPY 三轴的旋转拆分为三个独立四元数分别描述,此类操作无法解决万向锁问题,旋转后转换回欧拉角仍会出现维度丢失。
- 正确操作:将绕 RPY 三轴的三次变换视为单次整体旋转,采用单个四元数进行统一描述。
注:此处针对动态欧拉角场景。
- 四元数变换后需执行归一化(Normalize)处理,以维持其单位长度特性。
参考文献
- https://blog.youkuaiyun.com/hangl_ciom/article/details/98170231
- https://blog.youkuaiyun.com/lmonkey000/article/details/51001753
- https://baike.baidu.com/item/万向锁/15817326
- https://www.cnblogs.com/psklf/p/5656938.html
- https://www.cnblogs.com/psklf/p/5667593.html
- https://www.qiujiawei.com/quaternion3/
- https://www.qiujiawei.com/quaternion4/
- https://www.cnblogs.com/ymd12103410/p/9985063.html
旋转、旋转矩阵和欧拉角(内旋、外旋)
原创于 2024-04-25 20:44:39
在学习过程中,发现 “欧拉角的外旋等价于内旋的相反顺序” 这一结论易产生困惑。通过查阅资料并结合自身理解,整理成本文内容。若存在错误,欢迎指正。
1. 旋转坐标变换
旋转可分为对向量的旋转和对坐标系的旋转两类(坐标系由三个轴向量组成,本质上也是对向量的旋转)。以下对两类旋转进行详细说明,且不区分向量与坐标的表述。
1.1 对向量的旋转
此类旋转是最常见的形式,通常假设坐标系固定不动,旋转作用于物体本身。旋转后,坐标系位置保持不变,向量方向发生改变,即向量坐标值更新。其数学表达为:
t
1
=
f
(
t
)
\mathbf {t}_1 = f (\mathbf {t})
t1=f(t)
其中,
f
(
x
)
f (x)
f(x) 表示旋转操作(可通过旋转矩阵、四元数等实现),
t
\mathbf {t}
t 为三维空间向量,表达式为
(
a
,
b
,
c
)
T
(a, b, c)^T
(a,b,c)T,
a
,
b
,
c
a, b, c
a,b,c 分别为向量在坐标系三轴
(
u
,
v
,
w
)
(\mathbf {u}, \mathbf {v}, \mathbf {w})
(u,v,w) 上的分量。
1.2 对坐标系的旋转
此类旋转在机器人学中应用广泛,用于描述不同坐标系之间的旋转关系。忽略坐标系间的位置平移,仅考虑旋转时,坐标系的旋转表现为其三个轴向量的方向改变。
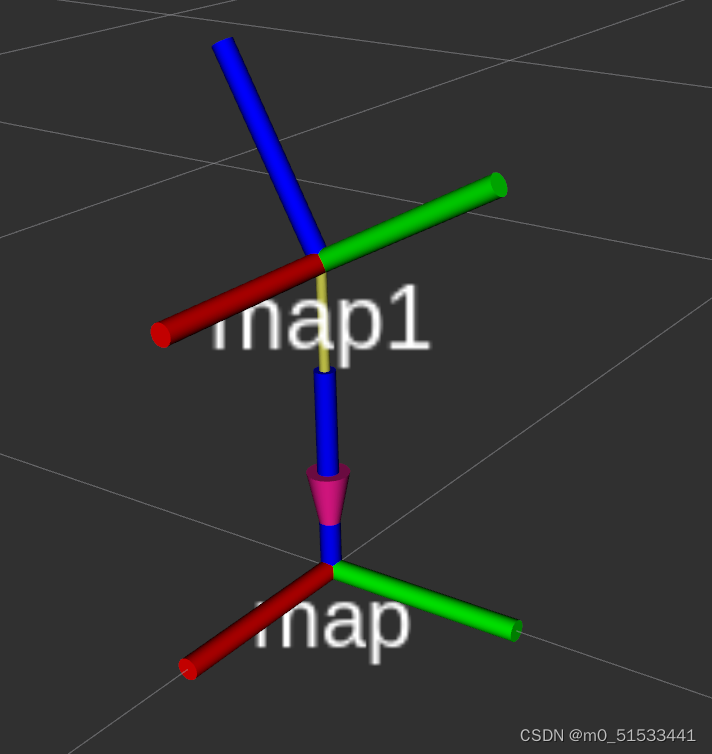
以上图中 map 坐标系与 map1 坐标系为例,map1 坐标系由 map 坐标系旋转得到。设 map 坐标系的三轴向量为
(
u
,
v
,
w
)
(\mathbf {u}, \mathbf {v}, \mathbf {w})
(u,v,w),旋转后 map1 坐标系的三轴向量为
(
u
1
,
v
1
,
w
1
)
(\mathbf {u}_1, \mathbf {v}_1, \mathbf {w}_1)
(u1,v1,w1),则旋转关系可表示为:
u
1
,
v
1
,
w
1
=
f
(
u
,
v
,
w
)
\mathbf {u}_1, \mathbf {v}_1, \mathbf {w}_1 = f (\mathbf {u}, \mathbf {v}, \mathbf {w})
u1,v1,w1=f(u,v,w)
令
A
=
(
u
,
v
,
w
)
\mathbf {A} = (\mathbf {u}, \mathbf {v}, \mathbf {w})
A=(u,v,w),
A
1
=
(
u
1
,
v
1
,
w
1
)
\mathbf {A}_1 = (\mathbf {u}_1, \mathbf {v}_1, \mathbf {w}_1)
A1=(u1,v1,w1),则上式可简化为:
A
1
=
f
(
A
)
\mathbf {A}_1 = f (\mathbf {A})
A1=f(A)
1.3 两种旋转方式的等价性
对向量的旋转与对坐标系的旋转本质上是等价的。对向量的旋转(坐标系固定)可等价为向量固定、坐标系沿反方向旋转。两种方式的最终结果一致,即向量相对于坐标系的方向变化相同,旋转后向量在坐标系中的表示形式相等。
| 初始图 | 旋转向量 | 旋转坐标系 |
|---|---|---|
 |  |  |
- 对向量旋转:旋转前向量坐标为 t \mathbf {t} t,旋转后坐标为 t 1 = f ( t ) \mathbf {t}_1 = f (\mathbf {t}) t1=f(t)。
- 对坐标系旋转:旋转前向量坐标为 t \mathbf {t} t,旋转后坐标系由 A \mathbf {A} A 变为 A 1 \mathbf {A}_1 A1,向量在新坐标系中的坐标 t 1 \mathbf {t}_1 t1 满足 A 1 t 1 = A t \mathbf {A}_1 \mathbf {t}_1 = \mathbf {A} \mathbf {t} A1t1=At,即 t 1 = A 1 − 1 A t \mathbf {t}_1 = \mathbf {A}_1^{-1} \mathbf {A} \mathbf {t} t1=A1−1At。
通过旋转矩阵可证明,两种方式得到的 t 1 \mathbf {t}_1 t1 完全相等。
2. 旋转矩阵
以下通过旋转矩阵的具体解析表达式,进一步解释两种旋转方式的等价性。
2.1 向量绕 Z 轴的旋转矩阵
对于向量
b
\mathbf {b}
b,从初始位置
b
1
\mathbf {b}_1
b1 绕 Z 轴逆时针旋转
θ
\theta
θ 角至
b
2
\mathbf {b}_2
b2,对应的旋转矩阵为:
R
=
[
cos
(
θ
)
−
sin
(
θ
)
0
sin
(
θ
)
cos
(
θ
)
0
0
0
1
]
\mathbf {R} = \begin {bmatrix} \cos (\theta) & -\sin (\theta) & 0 \\ \sin (\theta) & \cos (\theta) & 0 \\ 0 & 0 & 1 \end {bmatrix}
R=
cos(θ)sin(θ)0−sin(θ)cos(θ)0001
2.2 坐标系绕 Z 轴的旋转矩阵
设空间中存在全局坐标系 T \mathbf {T} T,向量 b \mathbf {b} b 在两个局部坐标系 T 1 = ( u 1 , v 1 , w 1 ) \mathbf {T}_1 = (\mathbf {u}_1, \mathbf {v}_1, \mathbf {w}_1) T1=(u1,v1,w1) 和 T 2 = ( u 2 , v 2 , w 2 ) \mathbf {T}_2 = (\mathbf {u}_2, \mathbf {v}_2, \mathbf {w}_2) T2=(u2,v2,w2) 中的表达式分别为 b 1 \mathbf {b}_1 b1 和 b 2 \mathbf {b}_2 b2(局部坐标系的轴向量均在全局坐标系 T \mathbf {T} T 下表示)。
由于向量在不同坐标系中的全局表达式相等,即 T 1 b 1 = T 2 b 2 = b \mathbf {T}_1 \mathbf {b}_1 = \mathbf {T}_2 \mathbf {b}_2 = \mathbf {b} T1b1=T2b2=b,可得 b 1 = T 1 − 1 T 2 b 2 \mathbf {b}_1 = \mathbf {T}_1^{-1} \mathbf {T}_2 \mathbf {b}_2 b1=T1−1T2b2。令 R = T 1 − 1 T 2 \mathbf {R} = \mathbf {T}_1^{-1} \mathbf {T}_2 R=T1−1T2(旋转矩阵),则 b 1 = R b 2 \mathbf {b}_1 = \mathbf {R} \mathbf {b}_2 b1=Rb2,表示坐标系从 T 2 \mathbf {T}_2 T2 旋转至 T 1 \mathbf {T}_1 T1 时向量的坐标变换。
若假设
T
1
\mathbf {T}_1
T1 与全局坐标系
T
\mathbf {T}
T 重合(基底为单位矩阵),则
R
=
T
2
\mathbf {R} = \mathbf {T}_2
R=T2,即
T
2
\mathbf {T}_2
T2 的基底为其轴向量在
T
1
\mathbf {T}_1
T1 下的表示。当
T
2
\mathbf {T}_2
T2 绕 Z 轴顺时针旋转
θ
\theta
θ 角得到
T
1
\mathbf {T}_1
T1 时,
T
2
\mathbf {T}_2
T2 在
T
1
\mathbf {T}_1
T1 下的表达式为:
T
2
=
[
cos
(
θ
)
−
sin
(
θ
)
0
sin
(
θ
)
cos
(
θ
)
0
0
0
1
]
\mathbf {T}_2 = \begin {bmatrix} \cos (\theta) & -\sin (\theta) & 0 \\ \sin (\theta) & \cos (\theta) & 0 \\ 0 & 0 & 1 \end {bmatrix}
T2=
cos(θ)sin(θ)0−sin(θ)cos(θ)0001
2.3 旋转矩阵的双重含义
上述旋转矩阵 R = [ cos ( θ ) − sin ( θ ) 0 sin ( θ ) cos ( θ ) 0 0 0 1 ] \mathbf {R} = \begin {bmatrix} \cos (\theta) & -\sin (\theta) & 0 \\ \sin (\theta) & \cos (\theta) & 0 \\ 0 & 0 & 1 \end {bmatrix} R= cos(θ)sin(θ)0−sin(θ)cos(θ)0001 具有双重含义:
- 向量绕 Z 轴逆时针旋转 θ \theta θ 角;
- 坐标系绕 Z 轴顺时针旋转 θ \theta θ 角。
两种旋转方式的等价性可通过下图直观展示:
 |  |  |  |
|---|
3. 欧拉角
欧拉角通过三个坐标轴的旋转分量描述刚体或坐标系在固定坐标系中的姿态,根据旋转轴类型(固定轴 / 运动轴)分为内旋和外旋。
3.1 基本概念
- 全局坐标系:旋转过程中固定不变的参考坐标系。
- 局部坐标系:固定于刚体上,随刚体同步运动的坐标系。
- 内旋(Intrinsic rotations):绕局部坐标系(运动轴)的旋转。
- 外旋(Extrinsic rotations):绕全局坐标系(固定轴)的旋转。
3.2 内旋(以 z → y → x z \to y \to x z→y→x 顺序为例)
内旋的旋转轴为局部坐标系轴,旋转过程中坐标轴随刚体同步更新。设旋转角度分别为 α \alpha α(绕 Z 轴)、 β \beta β(绕 Y 轴)、 γ \gamma γ(绕 X 轴),刚体的局部坐标系依次为 T 0 , T 1 , T 2 , T 3 \mathbf {T}_0, \mathbf {T}_1, \mathbf {T}_2, \mathbf {T}_3 T0,T1,T2,T3( T 0 \mathbf {T}_0 T0 与全局坐标系重合),刚体上某点在局部坐标系中的坐标为 p p p。
各步骤旋转矩阵
1.
T
0
→
T
1
\mathbf {T}_0 \to \mathbf {T}_1
T0→T1(绕
T
0
\mathbf {T}_0
T0 的 Z 轴旋转
α
\alpha
α):
R
01
=
R
z
(
α
)
=
[
cos
(
α
)
−
sin
(
α
)
0
sin
(
α
)
cos
(
α
)
0
0
0
1
]
\mathbf {R}_{01} = \mathbf {R}_z (\alpha) = \begin {bmatrix} \cos (\alpha) & -\sin (\alpha) & 0 \\ \sin (\alpha) & \cos (\alpha) & 0 \\ 0 & 0 & 1 \end {bmatrix}
R01=Rz(α)=
cos(α)sin(α)0−sin(α)cos(α)0001
点在
T
0
\mathbf {T}_0
T0 中的坐标:
p
0
1
=
R
01
p
p_0^1 = \mathbf {R}_{01} p
p01=R01p。
2.
T
1
→
T
2
\mathbf {T}_1 \to \mathbf {T}_2
T1→T2(绕
T
1
\mathbf {T}_1
T1 的 Y 轴旋转
β
\beta
β):
R
12
=
R
y
(
β
)
=
[
cos
(
β
)
0
sin
(
β
)
0
1
0
−
sin
(
β
)
0
cos
(
β
)
]
\mathbf {R}_{12} = \mathbf {R}_y (\beta) = \begin {bmatrix} \cos (\beta) & 0 & \sin (\beta) \\ 0 & 1 & 0 \\ -\sin (\beta) & 0 & \cos (\beta) \end {bmatrix}
R12=Ry(β)=
cos(β)0−sin(β)010sin(β)0cos(β)
点在
T
0
\mathbf {T}_0
T0 中的坐标:
p
0
2
=
R
01
R
12
p
p_0^2 = \mathbf {R}_{01} \mathbf {R}_{12} p
p02=R01R12p。
3.
T
2
→
T
3
\mathbf {T}_2 \to \mathbf {T}_3
T2→T3(绕
T
2
\mathbf {T}_2
T2 的 X 轴旋转
γ
\gamma
γ):
R
23
=
R
x
(
γ
)
=
[
1
0
0
0
cos
(
γ
)
−
sin
(
γ
)
0
sin
(
γ
)
cos
(
γ
)
]
\mathbf {R}_{23} = \mathbf {R}_x (\gamma) = \begin {bmatrix} 1 & 0 & 0 \\ 0 & \cos (\gamma) & -\sin (\gamma) \\ 0 & \sin (\gamma) & \cos (\gamma) \end {bmatrix}
R23=Rx(γ)=
1000cos(γ)sin(γ)0−sin(γ)cos(γ)
点在
T
0
\mathbf {T}_0
T0 中的坐标:
p
0
3
=
R
01
R
12
R
23
p
p_0^3 = \mathbf {R}_{01} \mathbf {R}_{12} \mathbf {R}_{23} p
p03=R01R12R23p。
总旋转矩阵
内旋的总旋转矩阵为各步骤旋转矩阵的右乘乘积:
R
内旋
=
R
z
(
α
)
R
y
(
β
)
R
x
(
γ
)
\mathbf {R}_{\text {内旋}} = \mathbf {R}_z (\alpha) \mathbf {R}_y (\beta) \mathbf {R}_x (\gamma)
R内旋=Rz(α)Ry(β)Rx(γ)
3.3 外旋(以 z → y → x z \to y \to x z→y→x 顺序为例)
外旋的旋转轴为全局坐标系轴,旋转过程中坐标轴保持固定。设旋转角度与内旋相同,刚体上某点初始坐标为 p 0 p_0 p0(在全局坐标系中)。
各步骤旋转矩阵
- 绕全局 Z 轴旋转 α \alpha α: p 1 = R z ( α ) p 0 p_1 = \mathbf {R}_z (\alpha) p_0 p1=Rz(α)p0
- 绕全局 Y 轴旋转 β \beta β: p 2 = R y ( β ) p 1 = R y ( β ) R z ( α ) p 0 p_2 = \mathbf {R}_y (\beta) p_1 = \mathbf {R}_y (\beta) \mathbf {R}_z (\alpha) p_0 p2=Ry(β)p1=Ry(β)Rz(α)p0
- 绕全局 X 轴旋转 γ \gamma γ: p 3 = R x ( γ ) p 2 = R x ( γ ) R y ( β ) R z ( α ) p 0 p_3 = \mathbf {R}_x (\gamma) p_2 = \mathbf {R}_x (\gamma) \mathbf {R}_y (\beta) \mathbf {R}_z (\alpha) p_0 p3=Rx(γ)p2=Rx(γ)Ry(β)Rz(α)p0
总旋转矩阵
外旋的总旋转矩阵为各步骤旋转矩阵的左乘乘积:
R
外旋
=
R
x
(
γ
)
R
y
(
β
)
R
z
(
α
)
\mathbf {R}_{\text {外旋}} = \mathbf {R}_x (\gamma) \mathbf {R}_y (\beta) \mathbf {R}_z (\alpha)
R外旋=Rx(γ)Ry(β)Rz(α)
3.4 内旋与外旋的关系
相同旋转顺序和角度下,内旋与外旋的总旋转矩阵互为逆序关系,即:
R
内旋
(
α
,
β
,
γ
)
=
R
外旋
(
γ
,
β
,
α
)
\mathbf {R}_{\text {内旋}}(\alpha, \beta, \gamma) = \mathbf {R}_{\text {外旋}}(\gamma, \beta, \alpha)
R内旋(α,β,γ)=R外旋(γ,β,α)
这一特性验证了 “欧拉角的外旋等价于内旋的相反顺序” 这一结论。
3.5 补充说明
- 内旋的向量旋转解释:理论上可通过向量旋转描述内旋,但除初始时刻外,局部坐标系与全局坐标系不重合,后续旋转矩阵在全局坐标系中的表达式会更复杂,需结合坐标变换进行推导。
- 外旋的坐标系旋转解释:同理,外旋也可通过坐标系旋转描述,但除初始时刻外,局部坐标系与全局坐标系不重合,后续旋转矩阵的表达式需结合轴向量的全局坐标进行计算,复杂度较高。
参考文献
游戏动画中欧拉角与万向锁的理解
huazai434 原创于 2011-05-31 23:21:00 发布
本文详细介绍欧拉角的概念,重点分析动态欧拉角中的万向锁现象,阐述其在游戏动画中引发的旋转限制与动画异常问题。通过具体实例解释万向锁的产生机理,并提出基于四元数插值的解决方案,为游戏开发中处理三维旋转问题提供理论依据与实践参考。
一、欧拉角的定义与分类
欧拉角是描述三维空间中刚体绕坐标系坐标轴旋转的角度集合,用于确定刚体相对参考坐标系的姿态。其显著特征在于依赖坐标系选择与旋转顺序,具体定义与分类如下:
1.1 基本定义
欧拉角通过刚体绕三个正交坐标轴(通常为 x x x 轴、 y y y 轴、 z z z 轴)的旋转角度来表示姿态,旋转顺序可灵活选择,常见组合包括 x y z xyz xyz、 x z y xzy xzy、 y x z yxz yxz、 z x y zxy zxy、 y z x yzx yzx、 z y x zyx zyx,特殊场景下也可采用 x y x xyx xyx、 x z z xzz xzz 等重复轴顺序,因此欧拉角的表示具有多样性。
1.2 分类方式
根据旋转所参考的坐标系是否随刚体运动,欧拉角可分为两类:
- 静态欧拉角:绕世界坐标系(固定不变的外部坐标系)的三个轴旋转。由于旋转过程中坐标轴方向保持静止,其旋转结果仅与初始姿态和旋转角度相关,不随刚体位置变化而改变。
- 动态欧拉角:绕物体坐标系(与刚体固连、随刚体运动的内部坐标系)的三个轴旋转。旋转过程中坐标轴随刚体同步运动,后一轴的旋转方向依赖于前一轴的旋转结果,因此旋转顺序对最终姿态影响显著。
1.3 旋转分解特性
根据欧拉旋转定理,刚体的任意旋转均可分解为绕三个正交轴的连续旋转,但分解方式不唯一。例如:设绕
y
y
y 轴旋转为 heading、绕
x
x
x 轴旋转为 pitch、绕
z
z
z 轴旋转为 bank,则 “先 heading
4
5
∘
45^\circ
45∘ 再 pitch
9
0
∘
90^\circ
90∘” 的旋转结果,与 “先 pitch
9
0
∘
90^\circ
90∘ 再 bank
4
5
∘
45^\circ
45∘” 的旋转结果完全等价。
二、万向锁现象的机理与表现
万向锁是动态欧拉角特有的问题,当特定旋转条件满足时,刚体将丢失一个旋转自由度,导致无法实现预期的三维旋转,其具体机理与表现如下:
2.1 触发条件
仅当使用动态欧拉角(绕物体坐标系旋转)时,若绕第二个旋转轴的角度为
±
9
0
∘
\pm90^\circ
±90∘(以常见的
z
y
x
zyx
zyx 旋转顺序为例,即 pitch 为
±
9
0
∘
\pm90^\circ
±90∘),无论前一轴(如
z
z
z 轴)和后一轴(如
x
x
x 轴)的旋转角度为何,均会触发万向锁。静态欧拉角因参考固定坐标系,不存在此问题。
2.2 实验验证(以手机为例)
为直观理解万向锁,可通过手机模拟刚体旋转,具体步骤如下:
- 坐标系定义:设手机平放于桌面时,物体坐标系的 z z z 轴垂直屏幕向上, x x x 轴沿手机短边向右, y y y 轴沿手机长边指向头部,原点为手机左下角顶点,旋转顺序为 z y x zyx zyx。
- 旋转操作:
- 第一步:绕 z z z 轴旋转任意角度( x x x 轴、 y y y 轴随手机同步旋转);
- 第二步:绕 y y y 轴旋转 9 0 ∘ 90^\circ 90∘;
- 第三步:绕 x x x 轴旋转任意角度。
- 现象观察:多次操作后可发现,手机的 z z z 轴始终保持水平,无法绕竖直方向旋转(即手机无法 “立起”),仅能在水平面内调整方向,此即万向锁的典型表现。
若第二步中绕 y y y 轴的旋转角度不为 9 0 ∘ 90^\circ 90∘(如 1 ∘ 1^\circ 1∘ 或 8 9 ∘ 89^\circ 89∘),则通过调整绕 x x x 轴和 z z z 轴的角度,可使手机指向三维空间中的任意方向,无自由度丢失。
2.3 本质原因
万向锁的本质是旋转轴重合导致自由度丢失:当绕第二个轴的旋转角度为 9 0 ∘ 90^\circ 90∘ 时,第三个旋转轴会被 “转到” 与第一个旋转轴的方向完全一致,原本相互正交的三个旋转轴退化为两个正交轴,刚体从三维旋转空间(3 个自由度)降至二维旋转空间(2 个自由度),丢失了沿重合轴方向的旋转能力(如上述实验中竖直方向的旋转自由度)。
三、游戏动画中的万向锁问题与影响
在游戏动画制作中,角色姿态与镜头运动依赖欧拉角的插值计算,万向锁会导致动画路径偏移与视觉异常,具体影响如下:
3.1 游戏动画的欧拉角应用逻辑
游戏动画中,角色的连续旋转无法通过存储所有姿态的欧拉角实现(数据量过大),通常采用 “关键帧插值” 方案:
- 动画师定义关键帧,每个关键帧用一组欧拉角描述角色的目标姿态;
- 计算机根据时间参数 t t t,对相邻关键帧的欧拉角进行线性插值,生成中间姿态的欧拉角;
- 按插值后的欧拉角驱动角色旋转,实现平滑动画效果。
3.2 万向锁引发的动画问题
当关键帧中存在触发万向锁的欧拉角(如 pitch 为
9
0
∘
90^\circ
90∘)时,动画表现会出现以下异常:
-
路径偏移:若下一个关键帧的姿态超出万向锁的二维约束范围(如要求角色 “立起”),欧拉角插值结果将偏离预期路径。例如:
- 设定 4 个关键帧的欧拉角(旋转顺序
z
y
x
zyx
zyx,逆时针为正方向,遵循右手法则,世界坐标系
z
z
z 轴向上、
x
x
x 轴向右、
y
y
y 轴指向观察者胸口):
关键帧 绕 z z z 轴旋转角度 绕 y y y 轴旋转角度 绕 x x x 轴旋转角度 R 0 R_0 R0 0 ∘ 0^\circ 0∘ 0 ∘ 0^\circ 0∘ 0 ∘ 0^\circ 0∘ R 1 R_1 R1 9 0 ∘ 90^\circ 90∘ 0 ∘ 0^\circ 0∘ 0 ∘ 0^\circ 0∘ R 2 R_2 R2 9 0 ∘ 90^\circ 90∘ − 9 0 ∘ -90^\circ −90∘ 0 ∘ 0^\circ 0∘ R 3 R_3 R3 0 ∘ 0^\circ 0∘ 0 ∘ 0^\circ 0∘ 9 0 ∘ 90^\circ 90∘ - 预期路径: R 0 → R 1 R_0 \to R_1 R0→R1(手机在桌面内逆时针转 9 0 ∘ 90^\circ 90∘)→ R 2 R_2 R2(手机右侧抬起至与桌面垂直)→ R 3 R_3 R3(手机竖直背向观察者);
- 实际路径: R 2 → R 3 R_2 \to R_3 R2→R3 插值时,因 R 2 R_2 R2 中绕 y y y 轴旋转为 − 9 0 ∘ -90^\circ −90∘(触发万向锁),插值后的姿态会偏离 “竖直背向” 目标,手机无法与桌面保持垂直。
- 设定 4 个关键帧的欧拉角(旋转顺序
z
y
x
zyx
zyx,逆时针为正方向,遵循右手法则,世界坐标系
z
z
z 轴向上、
x
x
x 轴向右、
y
y
y 轴指向观察者胸口):
-
镜头抖动:若万向锁发生在镜头控制中(如第三人称视角跟随角色旋转),插值路径的偏移会导致镜头视角频繁晃动,破坏游戏视觉连贯性与玩家沉浸感。
四、万向锁的解决方案:基于四元数的球面插值
万向锁的根源是欧拉角插值在三维空间中非线性,导致旋转路径失真。通过**四元数(Quaternion)**转换与球面线性插值(Slerp)可彻底解决此问题,具体方案如下:
4.1 原理说明
四元数是一种用于表示三维旋转的数学工具,由 1 个实部和 3 个虚部组成(形式为 q = w + x i + y j + z k q = w + xi + yj + zk q=w+xi+yj+zk,其中 w 2 + x 2 + y 2 + z 2 = 1 w^2 + x^2 + y^2 + z^2 = 1 w2+x2+y2+z2=1),其优势在于:
- 可唯一表示三维空间中的任意旋转,无欧拉角的多义性;
- 球面线性插值(Slerp)可在三维球面空间中实现平滑旋转,避免路径偏移;
- 不存在万向锁问题,可完整保留 3 个旋转自由度。
4.2 实现步骤
- 欧拉角转四元数:将关键帧中描述角色姿态的欧拉角,通过公式转换为对应的四元数。转换公式示例(以
z
y
x
zyx
zyx 旋转顺序为例,
α
\alpha
α 为绕
z
z
z 轴角度,
β
\beta
β 为绕
y
y
y 轴角度,
γ
\gamma
γ 为绕
x
x
x 轴角度):
w = cos ( α / 2 ) cos ( β / 2 ) cos ( γ / 2 ) + sin ( α / 2 ) sin ( β / 2 ) sin ( γ / 2 ) x = cos ( α / 2 ) cos ( β / 2 ) sin ( γ / 2 ) − sin ( α / 2 ) sin ( β / 2 ) cos ( γ / 2 ) y = cos ( α / 2 ) sin ( β / 2 ) cos ( γ / 2 ) + sin ( α / 2 ) cos ( β / 2 ) sin ( γ / 2 ) z = sin ( α / 2 ) cos ( β / 2 ) cos ( γ / 2 ) − cos ( α / 2 ) sin ( β / 2 ) sin ( γ / 2 ) \begin {align*} w &= \cos (\alpha/2)\cos (\beta/2)\cos (\gamma/2) + \sin (\alpha/2)\sin (\beta/2)\sin (\gamma/2) \\ x &= \cos (\alpha/2)\cos (\beta/2)\sin (\gamma/2) - \sin (\alpha/2)\sin (\beta/2)\cos (\gamma/2) \\ y &= \cos (\alpha/2)\sin (\beta/2)\cos (\gamma/2) + \sin (\alpha/2)\cos (\beta/2)\sin (\gamma/2) \\ z &= \sin (\alpha/2)\cos (\beta/2)\cos (\gamma/2) - \cos (\alpha/2)\sin (\beta/2)\sin (\gamma/2) \end {align*} wxyz=cos(α/2)cos(β/2)cos(γ/2)+sin(α/2)sin(β/2)sin(γ/2)=cos(α/2)cos(β/2)sin(γ/2)−sin(α/2)sin(β/2)cos(γ/2)=cos(α/2)sin(β/2)cos(γ/2)+sin(α/2)cos(β/2)sin(γ/2)=sin(α/2)cos(β/2)cos(γ/2)−cos(α/2)sin(β/2)sin(γ/2) - 四元数球面插值:对相邻关键帧的四元数执行 Slerp 操作,计算公式为:
Slerp ( q 0 , q 1 , t ) = sin ( ( 1 − t ) θ ) sin θ q 0 + sin ( t θ ) sin θ q 1 \text {Slerp}(q_0, q_1, t) = \frac {\sin ((1-t)\theta)}{\sin\theta} q_0 + \frac {\sin (t\theta)}{\sin\theta} q_1 Slerp(q0,q1,t)=sinθsin((1−t)θ)q0+sinθsin(tθ)q1
其中, q 0 q_0 q0、 q 1 q_1 q1 为相邻关键帧的四元数, t ∈ [ 0 , 1 ] t \in [0,1] t∈[0,1] 为时间参数, θ = arccos ( q 0 ⋅ q 1 ) \theta = \arccos (q_0 \cdot q_1) θ=arccos(q0⋅q1) 为两四元数的夹角。 - 四元数转欧拉角:将插值后的四元数转换回欧拉角,驱动角色或镜头旋转,实现平滑无偏移的动画效果。
4.3 方案优缺点
- 优点:彻底解决万向锁问题,旋转路径符合三维空间运动规律,动画平滑自然;
- 缺点:四元数的计算与存储需消耗额外内存(每个四元数需存储 4 个浮点数,欧拉角仅需 3 个),且数学逻辑较复杂,需开发者理解四元数的代数运算规则。
附录:万向锁现象参考视频
如需直观观察万向锁导致的路径偏移,可参考以下视频(视频通过万向节装置演示旋转轴重合与自由度丢失,与物体坐标系下的万向锁原理一致):
http://v.youku.com/v_show/id_XNzkyOTIyMTI=.html
via:
- 游戏动画中欧拉角与万向锁的理解_万向锁现象-优快云博客
https://blog.youkuaiyun.com/huazai434/article/details/6458257 - 【SLAM学习笔记1】欧拉角之万向锁问题(Gimbal Lock)-优快云博客
https://blog.youkuaiyun.com/weixin_46135347/article/details/116453491 - 关于万向锁(Gimbal lock)问题的理解及解决_万向锁问题-优快云博客
https://blog.youkuaiyun.com/weixin_43455581/article/details/108411948





















 511
511

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








