旋转变换 | 欧拉角、四元数、方向余弦矩阵

原创于 2025-12-06 17:17:32 发布 · 466 阅读

23 ·

CC 4.0 BY-SA版权

文章标签：

#旋转变换

electronic engineering 专栏收录该内容

79 篇文章

订阅专栏

注：本文为 “旋转变换” 相关合辑。
图片清晰度受引文原图所限。
略作重排，如有内容异常，请看原文。

四元数、欧拉角和方向余弦的定义及关系

wust_fly_high 于 2016-08-03 19:26:35 发布

本文系统地介绍了描述两个坐标系间关系的三种常见方法：欧拉角法、方向余弦矩阵法和四元数法。以四旋翼无人机为例，详细阐述了各方法的定义、计算过程及其相互之间的转换关系。

1. 坐标系的定义

描述两个坐标系之间关系时，需首先明确坐标系的定义。以四旋翼无人机为例，定义两个坐标系：导航坐标系（参考坐标系） $n$ 和载体坐标系（机体坐标系） $b$ 。导航坐标系 $n$ 采用东北天右手直角坐标系，载体坐标系 $b$ 亦为右手直角坐标系，其定义为：四轴向右为 $X$ 正方向，向前为 $Y$ 轴正方向，向上为 $Z$ 轴正方向。

2. 欧拉角的定义与计算

欧拉角是一种描述方位的方法，其基本思想是将两个坐标系的变换分解为绕三个不同坐标轴的三次连续转动。本文采用 Z-Y-X 旋转顺序来描述载体坐标系 $b$ 与导航坐标系 $n$ 的关系。具体而言，绕 $Z$ 轴旋转偏航角（YAW） $\psi$ ，绕 $Y$ 轴旋转横滚角（ROLL） $\phi$ ，绕 $X$ 轴旋转俯仰角（PITCH） $\theta$ 。

2.1 二维坐标系中的旋转关系

在二维 XY 坐标系中，假设载体坐标系 $b$ 和导航坐标系 $n$ 初始重合，绕 $X$ 轴逆时针旋转 $\theta$ 角。向量 $O A$ 在导航坐标系中的坐标为 $(Y, Z)$ ，在载体坐标系中的坐标为 $(Y^{'}, Z^{'})$ 。通过几何关系可得：

$\begin{cases} Y = Y' \cos \theta - Z' \sin \theta \\ Z = Y' \sin \theta + Z' \cos \theta \end{cases}$

写成矩阵形式为：

$\begin{bmatrix} Y \\ Z \end{bmatrix}= \begin{bmatrix} \cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \end{bmatrix} \begin{bmatrix} Y' \\ Z' \end{bmatrix}$

2.2 推广至三维坐标系

推广至三维坐标系，绕 $X$ 轴旋转的坐标关系为：

$\begin{bmatrix} X \\ Y \\ Z \end{bmatrix}= \begin{bmatrix} 1 & 0 & 0 \\ 0 & \cos \theta & -\sin \theta \\ 0 & \sin \theta & \cos \theta \end{bmatrix} \begin{bmatrix} X' \\ Y' \\ Z' \end{bmatrix}$

绕 $Y$ 轴旋转的坐标关系为：

$\begin{bmatrix} X \\ Y \\ Z \end{bmatrix}= \begin{bmatrix} \cos \phi & 0 & \sin \phi \\ 0 & 1 & 0 \\ -\sin \phi & 0 & \cos \phi \end{bmatrix} \begin{bmatrix} X' \\ Y' \\ Z' \end{bmatrix}$

绕 $Z$ 轴旋转的坐标关系为：

$\begin{bmatrix} X \\ Y \\ Z \end{bmatrix}= \begin{bmatrix} \cos \psi & -\sin \psi & 0 \\ \sin \psi & \cos \psi & 0 \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} X' \\ Y' \\ Z' \end{bmatrix}$

2.3 欧拉角的综合旋转矩阵

根据 Z-Y-X 旋转顺序，导航坐标系下的向量 $\begin{bmatrix} X^b \\ Y^b \\ Z^b \end{bmatrix}$ 与载体坐标系下的向量 $\begin{bmatrix} X^n \\ Y^n \\ Z^n \end{bmatrix}$ 之间的关系为：

$\begin{bmatrix} X^b \\ Y^b \\ Z^b \end{bmatrix}= \begin{bmatrix} 1 & 0 & 0 \\ 0 & \cos \theta & -\sin \theta \\ 0 & \sin \theta & \cos \theta \end{bmatrix} \begin{bmatrix} \cos \phi & 0 & \sin \phi \\ 0 & 1 & 0 \\ -\sin \phi & 0 & \cos \phi \end{bmatrix} \begin{bmatrix} \cos \psi & -\sin \psi & 0 \\ \sin \psi & \cos \psi & 0 \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} X^n \\ Y^n \\ Z^n \end{bmatrix}$

即：

$\begin{bmatrix} X^b \\ Y^b \\ Z^b \end{bmatrix}= R_n^b \begin{bmatrix} X^n \\ Y^n \\ Z^n \end{bmatrix}$

其中， $R_n^b$ 为坐标系 $n$ 到坐标系 $b$ 的变换矩阵。通常定义的欧拉角形式的方向余弦矩阵为 $R_b^n$ ，且 $R_b^n = (R_n^b)^T$ 。

$R_b^n = \begin{bmatrix} \cos \phi \cos \psi & \sin \theta \sin \phi \cos \psi - \cos \theta \sin \psi & \cos \theta \sin \phi \cos \psi + \sin \theta \sin \psi \\ \cos \phi \sin \psi & \sin \theta \sin \phi \sin \psi + \cos \theta \cos \psi & \cos \theta \sin \phi \sin \psi - \sin \theta \cos \psi \\ -\sin \phi & \sin \theta \cos \phi & \cos \theta \cos \phi \end{bmatrix}$

3. 四元数的定义与计算

四元数由四个元素构成，表示为 $Q(q_0, q_1, q_2, q_3) = q_0 + q_1 \vec{i} + q_2 \vec{j} + q_3 \vec{k}$ ，其中 $q_0, q_1, q_2, q_3$ 是实数， $\vec{i}, \vec{j}, \vec{k}$ 是互相正交的单位向量，同时也是虚单位 $\sqrt{-1}$ 。四元数的乘法规则为：

$\begin{cases} \vec{i} \otimes \vec{i} = -1 \\ \vec{j} \otimes \vec{j} = -1 \\ \vec{k} \otimes \vec{k} = -1 \\ \vec{i} \otimes \vec{j} = \vec{k} \\ \vec{j} \otimes \vec{k} = \vec{i} \\ \vec{k} \otimes \vec{i} = \vec{j} \\ \vec{j} \otimes \vec{i} = -\vec{k} \\ \vec{k} \otimes \vec{j} = -\vec{i} \\ \vec{i} \otimes \vec{k} = -\vec{j} \end{cases}$

其中， $\otimes$ 表示四元数乘法。具体展开为：

$\begin{aligned} Q(q_0, q_1, q_2, q_3) \otimes P(p_0, p_1, p_2, p_3) &= (q_0 + q_1 \vec{i} + q_2 \vec{j} + q_3 \vec{k}) \otimes (p_0 + p_1 \vec{i} + p_2 \vec{j} + p_3 \vec{k}) \\ &= (q_0 p_0 - q_1 p_1 - q_2 p_2 - q_3 p_3) + (q_0 p_1 + q_1 p_0 + q_2 p_3 - q_3 p_2) \vec{i} \\&\quad+ (q_0 p_2 + q_2 p_0 + q_3 p_1 - q_1 p_3) \vec{j} + (q_0 p_3 + q_3 p_0 + q_1 p_2 - q_2 p_1) \vec{k}\end{aligned}$

写成矩阵形式为：

$\begin{bmatrix} r_0 \\ r_1 \\ r_2 \\ r_3 \end{bmatrix}= \begin{bmatrix} q_0 & -q_1 & -q_2 & -q_3 \\ q_1 & q_0 & -q_3 & q_2 \\ q_2 & q_3 & q_0 & -q_1 \\ q_3 & -q_2 & q_1 & q_0 \end{bmatrix} \begin{bmatrix} p_0 \\ p_1 \\ p_2 \\ p_3 \end{bmatrix}= M(Q)P$

或者：

$\begin{bmatrix} r_0 \\ r_1 \\ r_2 \\ r_3 \end{bmatrix}= \begin{bmatrix} p_0 & -p_1 & -p_2 & -p_3 \\ p_1 & p_0 & -p_3 & p_2 \\ p_2 & p_3 & p_0 & -p_1 \\ p_3 & -p_2 & p_1 & p_0 \end{bmatrix} \begin{bmatrix} q_0 \\ q_1 \\ q_2 \\ q_3 \end{bmatrix}= M'(P)Q$

其中， $M (Q)$ 的构成形式为：第一列是四元数 $Q$ 本身，第一行是 $Q$ 的共轭四元数 $Q^*$ 的转置，剩下的部分是一个 3 行 3 列的矩阵 $V_Q$ ，称为 $M (Q)$ 的核，是由四元数构成的反对称矩阵：

$V_Q = \begin{bmatrix} q_0 & -q_3 & q_2 \\ q_3 & q_0 & -q_1 \\ -q_2 & q_1 & q_0 \end{bmatrix}$

同理可得 $M^{'} (P)$ 的核 $V_P$ ：

$V_P = \begin{bmatrix} p_0 & -p_3 & p_2 \\ p_3 & p_0 & -p_1 \\ -p_2 & p_1 & p_0 \end{bmatrix}$

3.1 四元数表示的旋转

定义四元数 $q_n^b$ 用于表示导航坐标系 $n$ 到载体坐标系 $b$ 的旋转变换，则有：

$r^n = q_b^n \otimes r^b \otimes q_b^{n*} = q_b^n \otimes (r^b \otimes q_b^{n*}) = q_b^n \otimes [M(q_b^{n*}) r^b] = M(q_b^n) M(q_b^{n*}) r^b$

$M(q_b^n) M(q_b^{n*}) = \begin{bmatrix} q_0 & -q_1 & -q_2 & -q_3 \\ q_1 & q_0 & -q_3 & q_2 \\ q_2 & q_3 & q_0 & -q_1 \\ q_3 & -q_2 & q_1 & q_0 \end{bmatrix} \begin{bmatrix} q_0 & q_1 & q_2 & q_3 \\ -q_1 & q_0 & -q_3 & q_2 \\ -q_2 & q_3 & q_0 & -q_1 \\ -q_3 & -q_2 & q_1 & q_0 \end{bmatrix}$

即：

$\begin{bmatrix} 0 \\ r_x^n \\ r_y^n \\ r_z^n \end{bmatrix}= \begin{bmatrix} q_0^2 + q_1^2 + q_2^2 + q_3^2 & 0 & 0 & 0 \\ 0 & q_0^2 + q_1^2 - q_2^2 - q_3^2 & 2(q_1 q_2 - q_0 q_3) & 2(q_0 q_2 + q_1 q_3) \\ 0 & 2(q_0 q_3 + q_1 q_2) & q_0^2 - q_1^2 + q_2^2 - q_3^2 & 2(q_2 q_3 - q_0 q_1) \\ 0 & 2(q_1 q_3 - q_0 q_2) & 2(q_0 q_1 + q_2 q_3) & q_0^2 - q_1^2 - q_2^2 + q_3^2 \end{bmatrix} \begin{bmatrix} 0 \\ r_x^b \\ r_y^b \\ r_z^b \end{bmatrix}$

简化为：

$\begin{bmatrix} r_x^n \\ r_y^n \\ r_z^n \end{bmatrix}= \begin{bmatrix} q_0^2 + q_1^2 - q_2^2 - q_3^2 & 2(q_1 q_2 - q_0 q_3) & 2(q_0 q_2 + q_1 q_3) \\ 2(q_0 q_3 + q_1 q_2) & q_0^2 - q_1^2 + q_2^2 - q_3^2 & 2(q_2 q_3 - q_0 q_1) \\ 2(q_1 q_3 - q_0 q_2) & 2(q_0 q_1 + q_2 q_3) & q_0^2 - q_1^2 - q_2^2 + q_3^2 \end{bmatrix} \begin{bmatrix} r_x^b \\ r_y^b \\ r_z^b \end{bmatrix}$

其中， $C_b^n$ 为通常定义的四元数旋转矩阵，表示载体坐标系 $b$ 到导航坐标系 $n$ 的旋转矩阵。

4. 四元数、欧拉角和方向余弦矩阵之间的关系

已知方向余弦矩阵和四元数旋转矩阵后，可通过方向余弦矩阵的第一列和第三行元素计算姿态欧拉角，具体公式如下：

$\begin{bmatrix}\theta \\\phi \\\psi\end{bmatrix}=\begin{bmatrix} \arctan 2(2 q_2 q_3 + 2 q_0 q_1, q_3^2 - q_2^2 - q_1^2 + q_0^2) \\ -\arcsin(2 q_1 q_3 - 2 q_0 q_2) \\ \arctan 2(2 q_1 q_2 + 2 q_0 q_3, q_1^2 + q_0^2 - q_3^2 - q_2^2) \end{bmatrix}$

以上内容对四元数、欧拉角和方向余弦矩阵的定义及其相互关系进行了系统阐述。

欧拉角与旋转矩阵的转换关系

陋室逢雨原创已于 2023-10-11 22:22:07 修改

欧拉角因存在奇异性，通常不用于优化与插值过程，但在描述旋转过程时具备直观性，例如无人机姿态控制领域常采用欧拉角表征姿态。明确欧拉角与旋转矩阵的转换关系是一项具有挑战性的工作，本文对此展开总结，以期助力相关概念的理解。

需明确每次旋转所绕的轴为固定轴还是旋转后的动轴，若无特殊说明，下文讨论均以绕旋转后的动轴旋转为前提。旋转顺序的选取不具有唯一性，采用 $Z Y X$ （先绕 $Z$ 轴、再绕 $Y$ 轴、最后绕 $X$ 轴）仅为使用习惯所致。绕单一坐标轴旋转某一角度亦可得到对应的旋转矩阵。

基础旋转矩阵：绕某一单一坐标轴进行旋转所对应的矩阵。
组合旋转矩阵：多次旋转操作组合后所对应的矩阵。

1、欧拉角的定义

定义一组欧拉角，需明确以下 5 条核心要素^[1]：

三个旋转角的组合方式；
旋转角度的参考坐标系统（旋转基于固定坐标系还是自身坐标系）；
旋转角度所采用的坐标系旋向（左手系或右手系）；
三个旋转角的记法规则；
旋转类型（主动旋转或被动旋转）。

1.1 欧拉角的旋转顺序（共12种）

经典欧拉角（Proper/classic Euler angle）：
$z$ - $x$ - $z$ 、 $x$ - $y$ - $x$ 、 $y$ - $z$ - $y$ 、 $z$ - $y$ - $z$ 、 $x$ - $z$ - $x$ 、 $y$ - $x$ - $y$ 。
泰特-布莱恩角（Tait-Bryan angle，亦称作 Cardan angles、nautical angles、heading-elevation-bank、yaw-pitch-roll）：
$x$ - $y$ - $z$ 、 $y$ - $z$ - $x$ 、 $z$ - $x$ - $y$ 、 $x$ - $z$ - $y$ 、 $z$ - $y$ - $x$ 、 $y$ - $x$ - $z$ 。

经典欧拉角的特征为三个旋转角并非完全独立，例如依次执行“绕 $x$ 轴旋转 $90^\circ$ 、绕 $y$ 轴旋转 $90^\circ$ 、绕 $x$ 轴旋转 $-90^\circ$ ”的旋转组合，其效果等价于仅绕 $z$ 轴旋转 $-90^\circ$ 。这表明仅在2个平面内完成旋转操作（其中一个平面需执行两次旋转），即可实现任意三维旋转。
在这里插入图片描述

1.2 内在旋转（intrinsic rotations）与外在旋转（extrinsic rotations）

内在旋转指每次旋转围绕的轴为上一次旋转后坐标系的坐标轴；外在旋转指每次旋转围绕的轴为固定坐标系的坐标轴。内在旋转与外在旋转的转换关系为：互换第一次与第三次旋转的顺序，二者最终得到的旋转矩阵相同。例如， $Z$ - $Y$ - $X$ 顺序的内在旋转与 $X$ - $Y$ - $Z$ 顺序的外在旋转所对应的旋转矩阵一致。
在这里插入图片描述

1.3 旋转角度的坐标系旋向（左手系/右手系）

以右手大拇指指向旋转轴，其余四指握拳的指向即为旋转角度的正方向：

右手系下，正角度对应逆时针旋转；
左手系下，正角度对应顺时针旋转。

1.4 主动旋转与被动旋转

主动旋转指将向量绕旋转轴逆时针旋转；被动旋转指对坐标轴进行逆时针旋转，其效果等价于主动旋转的逆操作。

2、不同轴的欧拉角转换为旋转矩阵

定义逆时针旋转为角度正方向（与右手系旋转方向一致），给出绕各坐标轴旋转的基础旋转矩阵：

$R_x(\theta)=\begin{bmatrix} 1 & 0 & 0 \\ 0 & \cos\theta & -\sin\theta \\ 0 & \sin\theta & \cos\theta \end{bmatrix}, \quad R_y(\phi)=\begin{bmatrix} \cos\phi & 0 & \sin\phi \\ 0 & 1 & 0 \\ -\sin\phi & 0 & \cos\phi \end{bmatrix}, \quad R_z(\psi)=\begin{bmatrix} \cos\psi & -\sin\psi & 0 \\ \sin\psi & \cos\psi & 0 \\ 0 & 0 & 1 \end{bmatrix}$

设存在坐标系 $b$ ，其内部有一点 $p$ （点与向量在空间中为同一几何对象，仅在指定坐标系时讨论其坐标，此处点 $p$ 的坐标亦记为 $p$ ）。若坐标系 $b$ 绕 $X$ 轴逆时针旋转 $\alpha$ 角度，求旋转后坐标系下点 $p$ 的坐标（记为 $p^{'}$ ）。通过数学推导^[2]可得：
$R_x(\alpha) \cdot p' = p \tag{1}$

对式 (1) 变形，得到：
$R_x^T(\alpha) \cdot p \tag{2}$

若从世界坐标系 $w$ 依次按 $Z Y X$ 顺序旋转得到坐标系 $b$ ，结合式 (2) 可推导坐标系 $b$ 相对于坐标系 $w$ 的旋转矩阵 $R_{bw}$ ：

$\begin{align*} R_{bw} &= R_x^T(\theta) \cdot R_y^T(\phi) \cdot R_z^T(\psi) \\ &= \begin{bmatrix} 1 & 0 & 0 \\ 0 & \cos\theta & -\sin\theta \\ 0 & \sin\theta & \cos\theta \end{bmatrix}^T \cdot \begin{bmatrix} \cos\phi & 0 & \sin\phi \\ 0 & 1 & 0 \\ -\sin\phi & 0 & \cos\phi \end{bmatrix}^T \cdot \begin{bmatrix} \cos\psi & -\sin\psi & 0 \\ \sin\psi & \cos\psi & 0 \\ 0 & 0 & 1 \end{bmatrix}^T \\ &= \begin{bmatrix} 1 & 0 & 0 \\ 0 & \cos\theta & \sin\theta \\ 0 & -\sin\theta & \cos\theta \end{bmatrix} \cdot \begin{bmatrix} \cos\phi & 0 & -\sin\phi \\ 0 & 1 & 0 \\ \sin\phi & 0 & \cos\phi \end{bmatrix} \cdot \begin{bmatrix} \cos\psi & \sin\psi & 0 \\ -\sin\psi & \cos\psi & 0 \\ 0 & 0 & 1 \end{bmatrix} \end{align*}$

$Z Y X$ 顺序旋转的物理意义为：坐标系 $b$ 在世界坐标系 $w$ 下的欧拉角，表征从 $w$ 系按该欧拉角顺序旋转可得到 $b$ 系。此时需求解的是世界坐标系 $w$ 相对于坐标系 $b$ 的旋转矩阵 $R_{wb}$ ，因此对 $R_{bw}$ 取转置：

$\begin{align*} R_{wb} &= R_{bw}^T \\ &= R_z(\psi) \cdot R_y(\phi) \cdot R_x(\theta) \\ &= \begin{bmatrix} \cos\psi & -\sin\psi & 0 \\ \sin\psi & \cos\psi & 0 \\ 0 & 0 & 1 \end{bmatrix} \cdot \begin{bmatrix} \cos\phi & 0 & \sin\phi \\ 0 & 1 & 0 \\ -\sin\phi & 0 & \cos\phi \end{bmatrix} \cdot \begin{bmatrix} 1 & 0 & 0 \\ 0 & \cos\theta & -\sin\theta \\ 0 & \sin\theta & \cos\theta \end{bmatrix} \end{align*}$

需注意，此处旋转矩阵的左乘顺序与旋转顺序相反，这也是VINS代码中采用的写法。同理，从旋转矩阵 $R_{wb}$ 转换为 $Z Y X$ 顺序的欧拉角时，该欧拉角表征 $b$ 系在 $w$ 系下的姿态，即从 $w$ 系（ $R_{wb}$ 的目标坐标系）变换至 $b$ 系（ $R_{wb}$ 的源坐标系）所采用的欧拉角。

从旋转矩阵反求欧拉角时，需采用与欧拉角转旋转矩阵相同的公式体系，以避免推导逻辑混乱。

3、旋转的本质

设坐标系 $b_1$ 内有一点 $p$ （坐标记为 $p$ ），依次执行“绕 $X$ 轴旋转 $\alpha$ 、绕 $Y$ 轴旋转 $\beta$ 、绕 $Z$ 轴旋转 $\gamma$ ”的操作后得到坐标系 $b_2$ ，推导旋转矩阵 $R_{b_2b_1}$ 的过程如下：

1）坐标系 $b_1$ 绕 $X$ 轴旋转 $\alpha$ ，得到新坐标系 $b_1'$ ，点 $p$ 在 $b_1'$ 下的坐标 $p^{'}$ 满足：
$R_x^T(\alpha) \cdot p$
亦可写作 $R_x(\alpha) \cdot p' = p$ ，但后续旋转操作基于当前旋转结果叠加，因此采用 $p^{'}$ 更便于后续推导。

2）坐标系 $b_1'$ 绕 $Y$ 轴旋转 $\beta$ ，得到新坐标系 $b_1''$ ，点 $p$ 在 $b_1''$ 下的坐标 $p^{''}$ 满足：
$R_y^T(\beta) \cdot p'$

3）坐标系 $b_1''$ 绕 $Z$ 轴旋转 $\gamma$ ，得到新坐标系 $b_1'''$ （即 $b_2$ ），点 $p$ 在 $b_1'''$ 下的坐标 $p^{'''}$ 满足：
$R_z^T(\gamma) \cdot p''$

将上述步骤合并，可得：
$R_z^T(\gamma) \cdot R_y^T(\beta) \cdot R_x^T(\alpha) \cdot p$

因此，坐标系 $b_2$ 相对于 $b_1$ 的旋转矩阵为：
$R_{b_2b_1} = R_z^T(\gamma) \cdot R_y^T(\beta) \cdot R_x^T(\alpha)$

上述推导方法适用于任意旋转组合的求解，因旋转具有叠加性（后续旋转矩阵左乘于当前结果）。例如，依次执行“绕 $X$ 轴旋转 $\alpha$ 、绕 $X$ 轴旋转 $\alpha'$ 、绕 $Y$ 轴旋转 $\beta$ 、绕 $X$ 轴旋转 $\alpha''$ ”的操作，其组合旋转矩阵为：
$R_x^T(\alpha'') \cdot R_y^T(\beta) \cdot R_x^T(\alpha') \cdot R_x^T(\alpha) = R_x^T(\alpha'') \cdot R_y^T(\beta) \cdot R_x^T(\alpha'+\alpha)$
其中，绕同一 $X$ 轴的旋转角 $\alpha$ 与 $\alpha'$ 可合并，原因是二者旋转轴相同。

4、内在旋转（ $Z$ - $Y$ - $X$ 顺序）对应的旋转矩阵

前文按 $X$ - $Y$ - $Z$ 旋转顺序推导得到：
$R_{b_2b_1} = R_z^T(\gamma) \cdot R_y^T(\beta) \cdot R_x^T(\alpha)$

将 $b_2$ 替换为 $b$ 、 $b_1$ 替换为 $w$ ，可得：
$R_{bw} = R_z^T(\gamma) \cdot R_y^T(\beta) \cdot R_x^T(\alpha)$

对 $R_{bw}$ 取转置，得到：
$R_{wb} = R_x(\alpha) \cdot R_y(\beta) \cdot R_z(\gamma)$

若旋转顺序改为 $Z$ - $Y$ - $X$ （从 $w$ 系到 $b$ 系的内在旋转），则对应的旋转矩阵为：
$R_{wb} = R_z(\gamma) \cdot R_y(\beta) \cdot R_x(\alpha)$

该结果与前文推导一致，需注意此为 $R_{wb}$ 而非 $R_{bw}$ ，相关验证见第6节。

5、内在旋转（ $Z$ - $Y$ - $X$ ）与外在旋转（ $X$ - $Y$ - $Z$ ）对应旋转矩阵相同的原因

外在旋转的旋转轴始终为固定坐标系 $w$ 的坐标轴。旋转前，坐标系 $w$ 与初始坐标系 $b_1$ 重合；旋转后，二者间存在旋转矩阵形式的外参。

1）绕 $w$ 系 $X$ 轴旋转，得到坐标系 $b_1'$ ，此时外参为：
$R_{b_1'w} = R_{w'w} = R_x^T(\alpha)$

2）接着绕 $w$ 系 $Y$ 轴旋转，得到坐标系 $b_1''$ ，此时 $R_{w'w}=R_y^T(\beta)$ ，结合外参转换可得：
$\begin{align*} R_{b_1''w} &= \left(R_{b_1'w} \cdot R_{w'w} \cdot R_{b_1'w}^T\right) \cdot R_{b_1'w} \\ &= R_x^T(\alpha) \cdot R_y^T(\beta) \cdot R_x(\alpha) \cdot R_x^T(\alpha) \\ &= R_x^T(\alpha) \cdot R_y^T(\beta) \end{align*}$

3）继续绕 $w$ 系 $Z$ 轴旋转，得到坐标系 $b_1'''$ ，此时：
$R_{b_1'''w} = R_x^T(\alpha) \cdot R_y^T(\beta) \cdot R_z^T(\gamma)$

对 $R_{b_1'''w}$ 取转置，得：
$R_{wb_1'''} = R_z(\gamma) \cdot R_y(\beta) \cdot R_x(\alpha)$

综上，绕固定轴的 $X$ - $Y$ - $Z$ 顺序外在旋转，与绕旋转后动轴的 $Z$ - $Y$ - $X$ 顺序内在旋转，二者对应的旋转矩阵等价。

6、验证：内在旋转（ $Z$ - $Y$ - $X$ ）得到的是 $R_{wb}$ 而非 $R_{bw}$

#include <Eigen/Core>
#include <Eigen/Geometry>
#include <iostream>
#include <cmath>

using namespace Eigen;
using namespace std;

Matrix3d zyxToRotationMatrix(Vector3d zyx)
{
    // 计算绕X轴旋转的旋转矩阵分量
    Matrix3d R_x;
    R_x << 1,            0,             0,
           0,  cos(zyx[2]),  -sin(zyx[2]),
           0,  sin(zyx[2]),   cos(zyx[2]);

    // 计算绕Y轴旋转的旋转矩阵分量
    Matrix3d R_y;
    R_y << cos(zyx[1]),  0,  sin(zyx[1]),
                     0,  1,            0,
          -sin(zyx[1]),  0,  cos(zyx[1]);

    // 计算绕Z轴旋转的旋转矩阵分量
    Matrix3d R_z;
    R_z << cos(zyx[0]),  -sin(zyx[0]),  0,
           sin(zyx[0]),   cos(zyx[0]),  0,
                     0,             0,  1;

    // 按Z-Y-X顺序左乘合并旋转矩阵
    Matrix3d R = R_z * R_y * R_x;
    return R;
}

int main()
{
    // 定义各轴旋转角度（Z轴0rad，Y轴π/6rad，X轴π/6rad）
    AngleAxisd r_z (      0, Vector3d ( 0,0,1 ) ); // 绕Z轴旋转
    AngleAxisd r_y ( M_PI/6, Vector3d ( 0,1,0 ) ); // 绕Y轴旋转
    AngleAxisd r_x ( M_PI/6, Vector3d ( 1,0,0 ) ); // 绕X轴旋转
    
    // 按Z-Y-X顺序构造四元数（内在旋转，绕旋转后动轴）
    Quaterniond q_zyx = r_z * r_y * r_x;                                    
    
    // 四元数转换为旋转矩阵（该矩阵为R_wb，表征从w系到b系的旋转）
    Matrix3d rotation_matrix = q_zyx.toRotationMatrix(); 
    cout << (rotation_matrix * Vector3d(1,0,0)).transpose() << endl;      
    cout << (rotation_matrix.transpose() * Vector3d(1,0,0)).transpose() << endl;

    // 欧拉角（Z-Y-X顺序）转换为旋转矩阵
    Vector3d euler_zyx(0, M_PI/6, M_PI/6);     
    rotation_matrix = zyxToRotationMatrix(euler_zyx); // 结果与四元数转换结果一致
    cout << (rotation_matrix * Vector3d(1,0,0)).transpose() << endl; 

    return 0;
}

输出结果

0.866025  -1.38778e-17 -0.5
0.866025   0.25         0.433013
0.866025   0           -0.5

将上述代码中的欧拉角可视化，结果如下图所示：
在这里插入图片描述

测试代码地址：https://github.com/LeatherWang/slam_car

参考文献

[1] csxiaoshui. 欧拉角定义的 5 个要素
https://blog.youkuaiyun.com/csxiaoshui/article/details/65437633.
[2] wkdwl. 旋转矩阵的数学推导
https://blog.youkuaiyun.com/wkdwl/article/details/52106646.

旋转矩阵与欧拉角之间的转换

卓晴原创已于 2022-02-27 19:02:33 修改

摘要：本文针对欧拉角与旋转矩阵间的转换公式及程序实现开展测试验证，分析了转换过程中由欧拉角的旋转方向、角度范围、旋转顺序所引入的复杂性，为实际工程应用中相关转换的正确实施提供参考。

关键词：欧拉角，旋转矩阵

在机器人视觉领域的应用中，常需完成旋转矩阵、旋转向量、四元数与欧拉角之间的相互转换，其中旋转矩阵与欧拉角的双向转换是易出现错误的环节。

▲ 图1 坐标系旋转变换

01 欧拉角

1.1 基本概念

1.1.1 欧拉角的名称

欧拉角的命名规则并非固定，与坐标轴的定义方式强相关：

若图1中 $X$ 轴为车头方向、 $Y$ 轴为车辆左侧方向、 $Z$ 轴为车辆上方方向，则绕 $X$ 轴的旋转角为横滚角（roll），绕 $Y$ 轴的旋转角为俯仰角（pitch），绕 $Z$ 轴的旋转角为偏航角（yaw）；
若图1中 $Y$ 轴为车头方向、 $X$ 轴为车辆右侧方向、 $Z$ 轴为车辆上方方向，则绕 $X$ 轴的旋转角为俯仰角（pitch），绕 $Y$ 轴的旋转角为横滚角（roll），绕 $Z$ 轴的旋转角为偏航角（yaw）。

1.1.2 欧拉角的旋转方向

右手系下，当观察者面向旋转轴正方向时，逆时针旋转为角度正方向，顺时针旋转为角度负方向；
另一种等价描述：以右手大拇指指向旋转轴正方向，其余四指握拳的指向即为旋转角度的正方向；
图1.1.1中所示的三次旋转均为正向旋转。

▲ 图1.1.1 三次旋转的过程

1.1.3 欧拉角的角度范围

欧拉角的角度范围需结合具体应用场景确定：

对于车体坐标系（ $x$ 轴向前、 $y$ 轴向左、 $z$ 轴向上），横滚角（roll）与俯仰角（pitch）的角度范围通常定义为 $(-90^\circ, +90^\circ)$ ，偏航角（yaw）的角度范围通常定义为 $(-180^\circ, +180^\circ)$ ；
对于飞机坐标系，横滚角（roll）、俯仰角（pitch）与偏航角（yaw）的角度范围通常均定义为 $(-180^\circ, +180^\circ)$ ；
Eigen 库中默认将 roll、pitch、yaw 的角度范围均设置为 $(-180^\circ, +180^\circ)$ 。

1.2 旋转顺序

1.2.1 旋转顺序与旋转轴

围绕 $x 、 y 、 z$ 三轴的旋转顺序共有6种组合： $x$ - $y$ - $z$ 、 $y$ - $z$ - $x$ 、 $z$ - $x$ - $y$ 、 $x$ - $z$ - $y$ 、 $z$ - $y$ - $x$ 、 $y$ - $x$ - $z$ 。即使旋转角度相同，不同旋转顺序得到的坐标系姿态也存在差异。例如，先绕 $x$ 轴旋转 $\alpha$ 再绕 $y$ 轴旋转 $\beta$ ，与先绕 $y$ 轴旋转 $\beta$ 再绕 $x$ 轴旋转 $\alpha$ ，两种操作得到的最终姿态不同。

1.2.2 内旋与外旋

外旋（外在旋转）：每次旋转围绕固定参考系（如世界坐标系）的坐标轴进行；
内旋（内在旋转）：每次旋转围绕自身坐标系经前次旋转后的坐标轴进行；
下图直观展示了内旋与外旋的区别。

▲ 图1.2.1 内在旋转

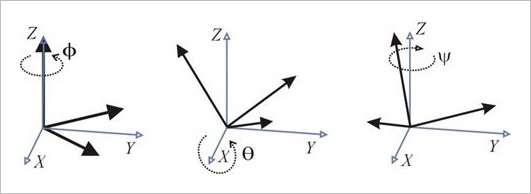
▲ 图1.2.2 外在旋转

按内旋方式执行 $Z$ - $Y$ - $X$ 顺序旋转（先绕自身 $Z$ 轴、再绕自身 $Y$ 轴、最后绕自身 $X$ 轴），对应的旋转矩阵为（内旋采用右乘规则）：
$R_1 = R_z \left( \gamma \right) \cdot R_y \left( \beta \right) \cdot R_x \left( \alpha \right)$

按外旋方式执行 $X$ - $Y$ - $Z$ 顺序旋转（先绕固定 $X$ 轴、再绕固定 $Y$ 轴、最后绕固定 $Z$ 轴），对应的旋转矩阵为（外旋采用左乘规则）：
$R_2 = R_z \left( \gamma \right) \cdot R_y \left( \beta \right) \cdot R_x \left( \alpha \right)$

由此可得 $R_1=R_2$ （证明过程略），该结论表明： $Z$ - $Y$ - $X$ 顺序的内旋与 $X$ - $Y$ - $Z$ 顺序的外旋等价。

02 旋转矩阵

2.1 由欧拉角到旋转矩阵

设绕 $X 、 Y 、 Z$ 三轴的旋转角度分别为 $\alpha、\beta、\gamma$ ，则单次绕轴旋转对应的基础旋转矩阵如下：

▲ 图2.1 三个旋转矩阵

$R_x \left( \theta \right) = \begin{bmatrix} 1 & 0 & 0 \\ 0 & \cos\theta & -\sin\theta \\ 0 & \sin\theta & \cos\theta \end{bmatrix}$

$R_y \left( \theta \right) = \begin{bmatrix} \cos\theta & 0 & \sin\theta \\ 0 & 1 & 0 \\ -\sin\theta & 0 & \cos\theta \end{bmatrix}$

$R_z \left( \theta \right) = \begin{bmatrix} \cos\theta & -\sin\theta & 0 \\ \sin\theta & \cos\theta & 0 \\ 0 & 0 & 1 \end{bmatrix}$

2.2 绕任意轴的旋转矩阵

若绕过原点且单位化的向量 $\boldsymbol{U} = \left( U_x , U_y , U_z \right)$ 旋转 $\theta$ 角度，对应的旋转矩阵为：
$R_U \left( \theta \right) = \boldsymbol{I} + \left( \sin \theta \right) \cdot \boldsymbol{S} + \left( 1 - \cos \theta \right) \cdot \boldsymbol{S}^2$

其中：

$\boldsymbol{I}$ 为 3×3 单位矩阵；
反对称矩阵 $\boldsymbol{S}$ 定义为：
$\boldsymbol{S} = \begin{bmatrix} 0 & -U_z & U_y \\ U_z & 0 & -U_x \\ -U_y & U_x & 0 \end{bmatrix}$

▲ 图2.2 旋转角与旋转矩阵

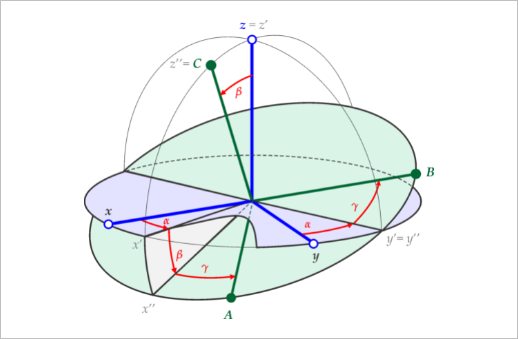
03 旋转矩阵与欧拉角的相互转换

3.1 转换公式

▲ 图3.1.1 欧拉角与转换过程

3.1.1 从欧拉角到旋转矩阵

《Euler Angle Formulas》^[1] 给出了不同参数设置下欧拉角到旋转矩阵的转换公式。

▲ 图3.2.1 从欧拉角到旋转矩阵

▲ 图3.2.2 欧拉角

3.2 转换代码实现

3.2.1 Python 代码

参考《Rotation matrix to Euler angles Python code example》^[2] 实现如下转换：

（1）旋转矩阵转换为欧拉角

import numpy as np
import math

def isRotationMatrix(R) :
    Rt = np.transpose(R)
    shouldBeIdentity = np.dot(Rt, R)
    I = np.identity(3, dtype = R.dtype)
    n = np.linalg.norm(I - shouldBeIdentity)
    return n < 1e-6

def rotationMatrixToEulerAngles(R) :
    assert(isRotationMatrix(R))
    sy = math.sqrt(R[0,0] * R[0,0] +  R[1,0] * R[1,0])
    singular = sy < 1e-6
    if  not singular :
        x = math.atan2(R[2,1] , R[2,2])
        y = math.atan2(-R[2,0], sy)
        z = math.atan2(R[1,0], R[0,0])
    else :
        x = math.atan2(-R[1,2], R[1,1])
        y = math.atan2(-R[2,0], sy)
        z = 0
    return np.array([x, y, z])

（2）欧拉角转换为旋转矩阵

import numpy as np
import math

def euler_to_rotVec(yaw, pitch, roll):
    Rmat = euler_to_rotMat(yaw, pitch, roll)

    theta = math.acos(((Rmat[0, 0] + Rmat[1, 1] + Rmat[2, 2]) - 1) / 2)
    sin_theta = math.sin(theta)
    if sin_theta == 0:
        rx, ry, rz = 0.0, 0.0, 0.0
    else:
        multi = 1 / (2 * math.sin(theta))
        rx = multi * (Rmat[2, 1] - Rmat[1, 2]) * theta
        ry = multi * (Rmat[0, 2] - Rmat[2, 0]) * theta
        rz = multi * (Rmat[1, 0] - Rmat[0, 1]) * theta
    return rx, ry, rz

def euler_to_rotMat(yaw, pitch, roll):
    Rz_yaw = np.array([
        [np.cos(yaw), -np.sin(yaw), 0],
        [np.sin(yaw),  np.cos(yaw), 0],
        [          0,            0, 1]])
    Ry_pitch = np.array([
        [ np.cos(pitch), 0, np.sin(pitch)],
        [             0, 1,             0],
        [-np.sin(pitch), 0, np.cos(pitch)]])
    Rx_roll = np.array([
        [1,            0,             0],
        [0, np.cos(roll), -np.sin(roll)],
        [0, np.sin(roll),  np.cos(roll)]])
    rotMat = np.dot(Rz_yaw, np.dot(Ry_pitch, Rx_roll))
    return rotMat

测试验证可得各角度对应的旋转轴：

yaw：对应 $z$ 轴旋转角；
pitch：对应 $y$ 轴旋转角；
roll：对应 $x$ 轴旋转角。

3.2.2 基于 SciPy 库的实现

参考 SciPy 官方文档 ^[3] 中 scipy.spatial.transform.Rotation.from_euler 接口实现转换：

import sys, os, math, time
import matplotlib.pyplot as plt
import numpy as np
from scipy.spatial.transform import Rotation as R

r = R.from_euler('x', 90, degrees=True)
print("r.as_quat(): {}".format(r.as_quat()))

运行结果：

r.as_quat(): [0.70710678 0.         0.         0.70710678]

Rotation 类的核心方法包括：

'apply', 'as_dcm', 'as_euler', 'as_quat', 'as_rotvec', 
'from_dcm', 'from_euler', 'from_quat', 'from_rotvec', 'inv', 'match_vectors'

3.3 代码结果对比

import numpy as np
import math
from scipy.spatial.transform import Rotation as R

# 定义旋转角度（单位：度）
x = 30
y = 45
z = 60

# 基于SciPy的转换
r = R.from_euler('zyx', [-z, -y, -x], degrees=True)
print("r.as_dcm():\n{}".format(r.as_dcm()))

# 自定义函数的转换
rm = euler_to_rotMat(z * np.pi/180, y * np.pi/180, x * np.pi/180)
print("rm.T:\n{}".format(rm.T))

运行结果：

r.as_dcm():
[[ 0.35355339  0.61237244 -0.70710678]
 [-0.5732233   0.73919892  0.35355339]
 [ 0.73919892  0.28033009  0.61237244]]
rm.T:
[[ 0.35355339  0.61237244 -0.70710678]
 [-0.5732233   0.73919892  0.35355339]
 [ 0.73919892  0.28033009  0.61237244]]

结果表明，两种方法对角度正负的定义存在差异，输出矩阵呈转置关系。进一步验证：

rm = euler_to_rotMat(z * np.pi/180, y * np.pi/180, x * np.pi/180)
print("rm.T:\n{}".format(rm.T))

r = R.from_dcm(rm.T)
print("r.as_euler('zyx')*180/np.pi: {}".format(r.as_euler('zyx')*180/np.pi))

运行结果：

rm.T:
[[ 0.35355339  0.61237244 -0.70710678]
 [-0.5732233   0.73919892  0.35355339]
 [ 0.73919892  0.28033009  0.61237244]]
r.as_euler('zyx')*180/np.pi: [-60. -45. -30.]

※ 总结 ※

本文完成了欧拉角与旋转矩阵转换公式及程序实现的测试验证，分析表明二者转换关系的复杂性主要源于欧拉角的旋转方向、角度范围与旋转顺序的差异，在实际应用中需重点关注这些参数的一致性定义。

完整测试代码

#!/usr/local/bin/python
# -*- coding: gbk -*-
#============================================================
# TEST4.PY                     -- by Dr. ZhuoQing 2021-12-31
#
# Note:
#============================================================

from headm import *                 # 自定义头文件
from scipy.spatial.transform import Rotation as R
import numpy as np
import math

# 欧拉角转旋转向量
def euler_to_rotVec(yaw, pitch, roll):
    Rmat = euler_to_rotMat(yaw, pitch, roll)

    theta = math.acos(((Rmat[0, 0] + Rmat[1, 1] + Rmat[2, 2]) - 1) / 2)
    sin_theta = math.sin(theta)
    if sin_theta == 0:
        rx, ry, rz = 0.0, 0.0, 0.0
    else:
        multi = 1 / (2 * math.sin(theta))
        rx = multi * (Rmat[2, 1] - Rmat[1, 2]) * theta
        ry = multi * (Rmat[0, 2] - Rmat[2, 0]) * theta
        rz = multi * (Rmat[1, 0] - Rmat[0, 1]) * theta
    return rx, ry, rz

# 欧拉角转旋转矩阵
def euler_to_rotMat(yaw, pitch, roll):
    Rz_yaw = np.array([
        [np.cos(yaw), -np.sin(yaw), 0],
        [np.sin(yaw),  np.cos(yaw), 0],
        [          0,            0, 1]])
    Ry_pitch = np.array([
        [ np.cos(pitch), 0, np.sin(pitch)],
        [             0, 1,             0],
        [-np.sin(pitch), 0, np.cos(pitch)]])
    Rx_roll = np.array([
        [1,            0,             0],
        [0, np.cos(roll), -np.sin(roll)],
        [0, np.sin(roll),  np.cos(roll)]])
    rotMat = np.dot(Rz_yaw, np.dot(Ry_pitch, Rx_roll))
    return rotMat

# 定义旋转角度
x = 30
y = 45
z = 60

# SciPy库转换
r = R.from_euler('zyx', [-z, -y, -x], degrees=True)
printt(r.as_dcm())

# 自定义函数转换
rm = euler_to_rotMat(z * np.pi/180, y * np.pi/180, x * np.pi/180)
printt(rm.T)

# 反向验证
rm = euler_to_rotMat(z * np.pi/180, y * np.pi/180, x * np.pi/180)
printt(rm.T)

r = R.from_dcm(rm.T)
printt(r.as_euler('zyx')*180/np.pi)

#        END OF FILE : TEST4.PY
#============================================================