注:本文为 “线性代数 | 要义 / 本质” 相关合辑。
略排未全校,如有内容异常,请看原文。
- 线性代数 | 要义 / 本质 (上篇)-优快云博客
https://blog.youkuaiyun.com/u013669912/article/details/153110982
【直观详解】线性代数的本质(下篇)
5 行列式的几何意义
The purpose of computation is insight, not numbers - Richard Hamming
计算的目的不在于数字本身,而在于洞察其背后的意义 ——理查德·汉明(没错,是发明汉明码的那个人)
5.1 行列式的定义
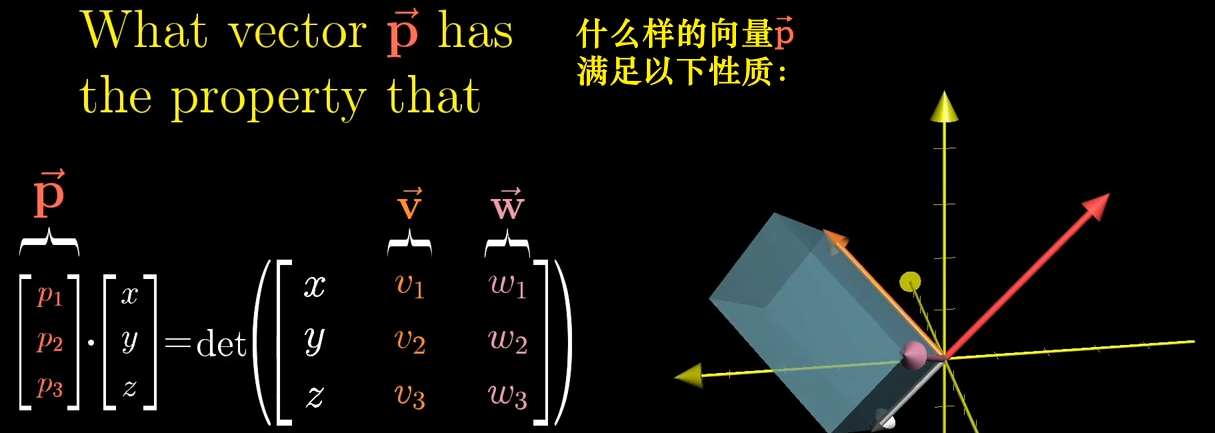
行列式是衡量线性变换对空间体积(面积 / 体积)缩放比例的指标,记为 det ( A ) \det (A) det(A) 或 ∣ A ∣ |A| ∣A∣。
-
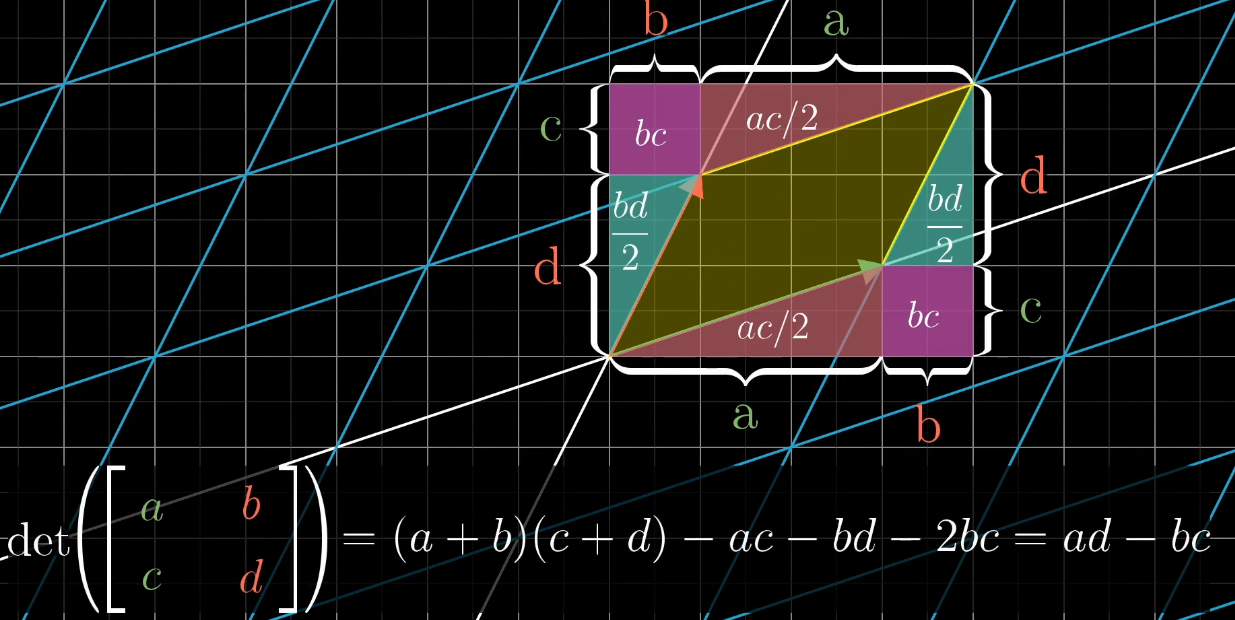
二维空间:对于矩阵 A = [ a b c d ] A = \begin {bmatrix} a & b \\ c & d \end {bmatrix} A=[acbd],其行列式为 det ( A ) = a d − b c \det (A) = ad - bc det(A)=ad−bc,几何意义是 “标准基 { ı ^ , ȷ ^ } \{\hat {\imath}, \hat {\jmath}\} {^,^} 构成的单位正方形,经 A A A 变换后形成的平行四边形的面积”;
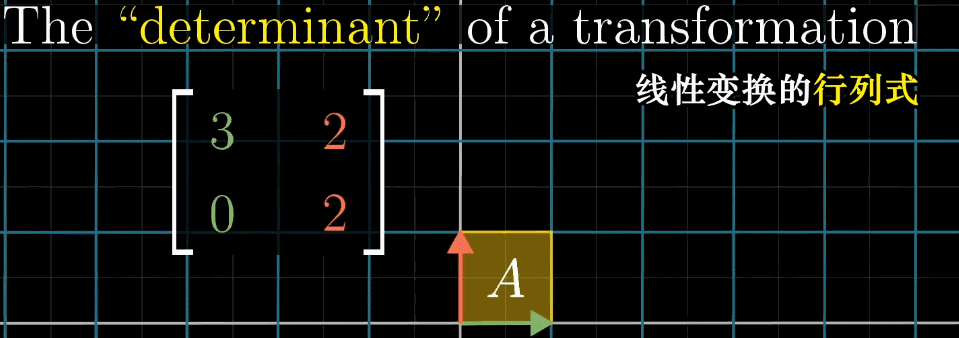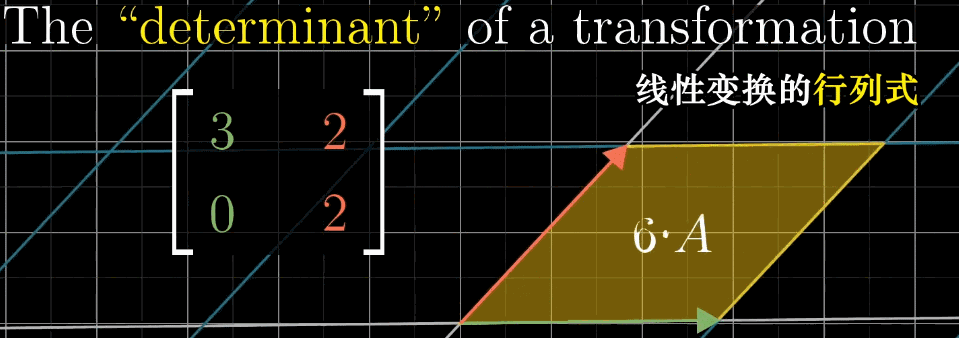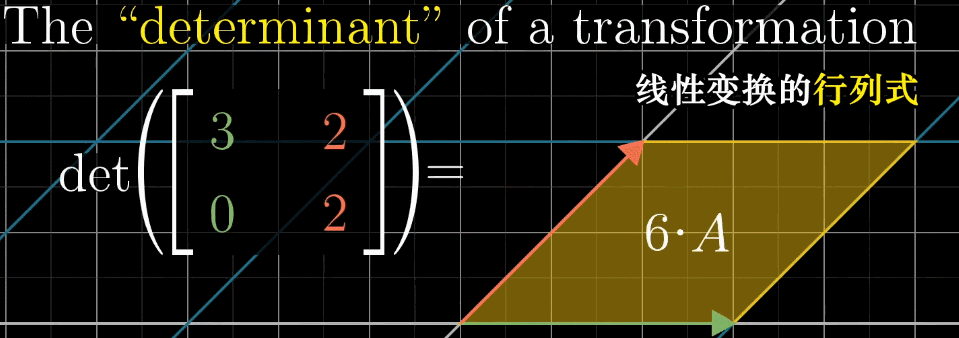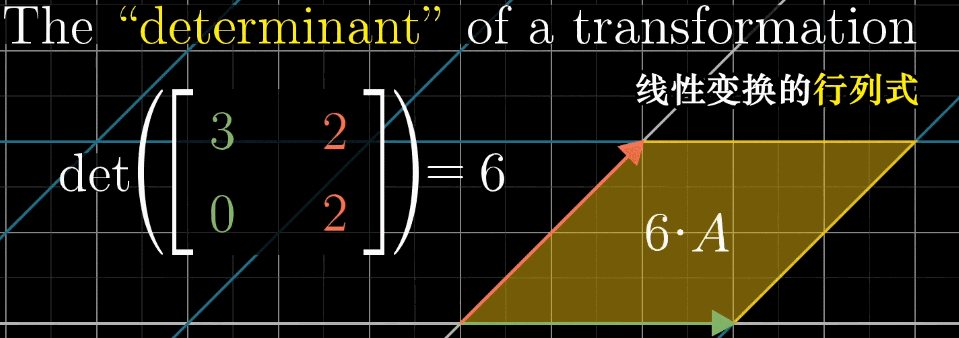
-
三维空间:对于矩阵 A = [ a b c d e f g h i ] A = \begin {bmatrix} a & b & c \\ d & e & f \\ g & h & i \end {bmatrix} A= adgbehcfi ,其行列式为 det ( A ) = a ( e i − f h ) − b ( d i − f g ) + c ( d h − e g ) \det (A) = a (ei - fh) - b (di - fg) + c (dh - eg) det(A)=a(ei−fh)−b(di−fg)+c(dh−eg),几何意义是 “标准基 { ı ^ , ȷ ^ , k ^ } \{\hat {\imath}, \hat {\jmath}, \hat {k}\} {^,^,k^} 构成的单位立方体,经 A A A 变换后形成的平行六面体的体积”。
5.2 行列式的符号与降维
5.2.1 行列式的符号意义
行列式的正负表示线性变换是否改变空间的“定向”,具体判断方式随空间维度不同而变化:
- 二维空间:以单位向量 ı ^ \hat{\imath} ^ 为参照,若 ȷ ^ \hat{\jmath} ^ 经变换后从 ı ^ \hat{\imath} ^ 的左侧转移至右侧(效果类似“纸的翻面”),则行列式为负;反之, ȷ ^ \hat{\jmath} ^ 相对 ı ^ \hat{\imath} ^ 方位不变,行列式为正。
- 三维空间:空间定向通过右手定则判断——右手四指沿 ı ^ → ȷ ^ → k ^ \hat{\imath} \to \hat{\jmath} \to \hat{k} ^→^→k^ 顺序弯曲,大拇指指向为空间正定向。变换后定向方向相反,行列式为负;定向方向不变,行列式为正。
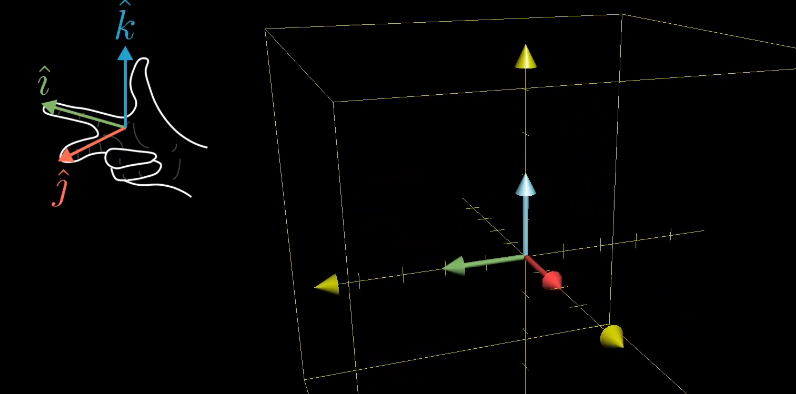
5.2.2 行列式与空间降维的关系
若矩阵 A A A 的行列式 det ( A ) = 0 \det(A) = 0 det(A)=0,则该矩阵对应的线性变换会导致空间维度降低:
- 二维空间变换后降为直线;
- 三维空间变换后降为平面或直线。
其本质是: det ( A ) = 0 \det(A) = 0 det(A)=0 时,矩阵 A A A 的列向量线性相关,张成的空间维度小于矩阵阶数(如二阶矩阵列向量张成一维空间,三阶矩阵列向量张成二维或一维空间)。
5.2.3 线性变换的性质与行列式的作用
-
线性变换的基本性质:
线性变换保持图形的平行性,但改变图形的大小与方向;且不必然保持形状——仅旋转、反射等特殊线性变换保形,剪切变换等会改变图形形状。 -
行列式在二维线性变换中的作用:
行列式是描述矩阵缩放作用的标量值,可确定二维线性变换的两个关键结果:- 判断朝向变化:行列式为正,图形朝向不变;行列式为负,图形朝向反转。
- 确定面积缩放比例:行列式的绝对值等于面积缩放比例。绝对值为 1 时面积不变,大于 1 时面积放大,小于 1 时面积缩小。
5.3 行列式的重要性质
由几何意义可直接推导行列式的核心性质:
-
det ( M 1 M 2 ) = det ( M 1 ) det ( M 2 ) \det (M_1M_2) = \det (M_1)\det (M_2) det(M1M2)=det(M1)det(M2):复合变换的体积缩放比例等于各变换缩放比例的乘积;
-
det ( A − 1 ) = 1 det ( A ) \det (A^{-1}) = \frac {1}{\det (A)} det(A−1)=det(A)1:逆变换的缩放比例是原变换的倒数(若原变换放大 k k k 倍,逆变换缩小 1 k \frac {1}{k} k1 倍);
-
det ( k A ) = k n det ( A ) \det (kA) = k^n\det (A) det(kA)=kndet(A): n n n 阶矩阵的数乘变换,体积缩放比例为 k n k^n kn(二维:面积缩放 k 2 k^2 k2,三维:体积缩放 k 3 k^3 k3)。
行列式直观理解
行列式是矩阵的一个数值特征,为建立行列式计算公式与几何直观的联系,二阶矩阵 [ a b c d ] \begin{bmatrix} a&b\\ c&d\end{bmatrix} [acbd] 的行列式,对应其列向量张成图形的有向面积:
-
当 b = c = 0 b = c = 0 b=c=0 时,矩阵为 [ a 0 0 d ] \begin{bmatrix} a&0\\ 0&d\end{bmatrix} [a00d], a a a 是 i ^ \hat{i} i^ 在 x x x 轴的缩放比例, d d d 是 j ^ \hat{j} j^ 在 y y y 轴的缩放比例,行列式 a d ad ad 是单位正方形按 a a a、 d d d 拉伸后的面积(拉伸倍数)。
-
当 b b b、 c c c 非 0 0 0 时,行列式 a d − b c ad - bc ad−bc 综合了 x x x、 y y y 轴拉伸与图形“倾斜压缩”的效果,为变换后图形的有向面积(总缩放比例)。
6 逆矩阵、列空间与零空间
To ask the right question is harder than to answer it - Georg Cantor
提出正确的问题比回答它更难 ——格奥尔格·康托尔
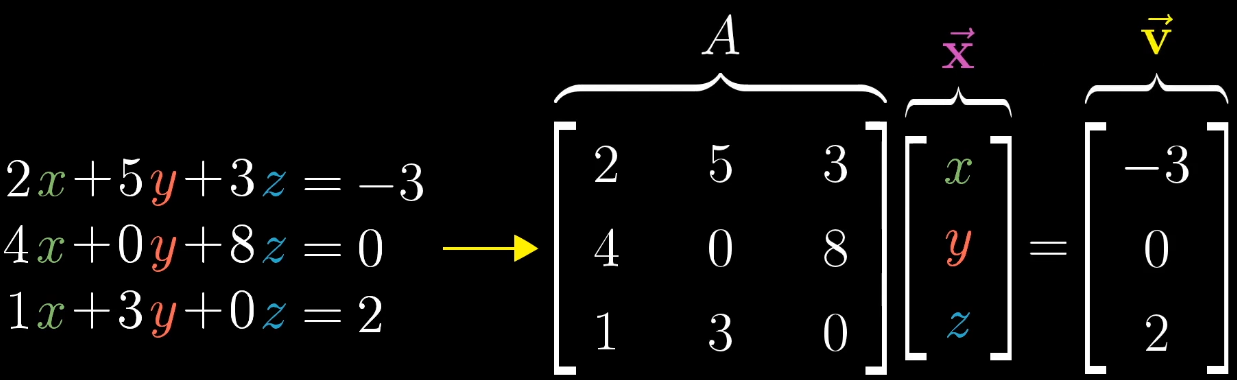
6.1 线性方程组的几何意义
线性方程组的一般形式为 A x ⃗ = v ⃗ A\vec {x} = \vec {v} Ax=v,其中 A A A 为 n × n n \times n n×n 矩阵, x ⃗ \vec {x} x 为待求向量,
几何直观来翻译个公式即 A x ⃗ A\vec {x} Ax 经过 A A A 矩阵变换后,恰好落在 v ⃗ \vec {v} v 上
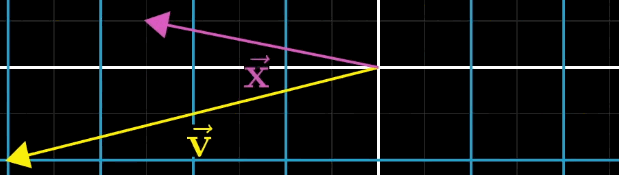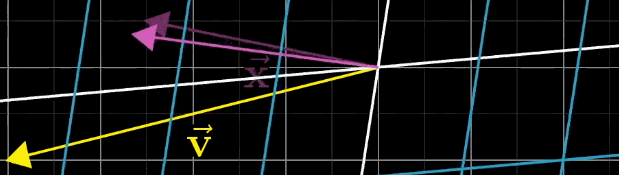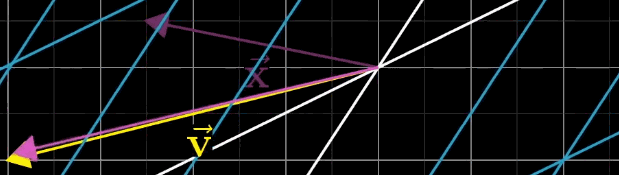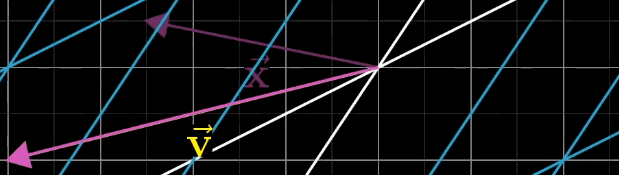
从线性变换的角度,该方程的几何意义是:找到向量 x ⃗ \vec {x} x,使其经 A A A 变换后恰好等于 v ⃗ \vec {v} v。
6.2 逆矩阵与方程组求解
6.2.1 逆矩阵的定义
若存在矩阵 A − 1 A^{-1} A−1,使得 A − 1 A = I A^{-1} A = I A−1A=I( I I I 为单位矩阵, I = [ 1 0 0 1 ] I = \begin {bmatrix} 1 & 0 \\ 0 & 1 \end {bmatrix} I=[1001](二维), I = [ 1 0 0 0 1 0 0 0 1 ] I = \begin {bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end {bmatrix} I= 100010001 (三维)),则称 A − 1 A^{-1} A−1 为 A A A 的逆矩阵。
- 几何意义:
A
−
1
A^{-1}
A−1 对应的变换是
A
A
A 的 “逆操作”—— 若
A
A
A 将
x
⃗
\vec {x}
x 变换为
v
⃗
\vec {v}
v,则
A
−
1
A^{-1}
A−1 将
v
⃗
\vec {v}
v 变换回
x
⃗
\vec {x}
x。
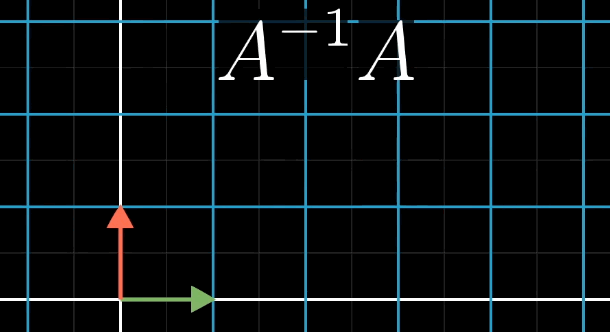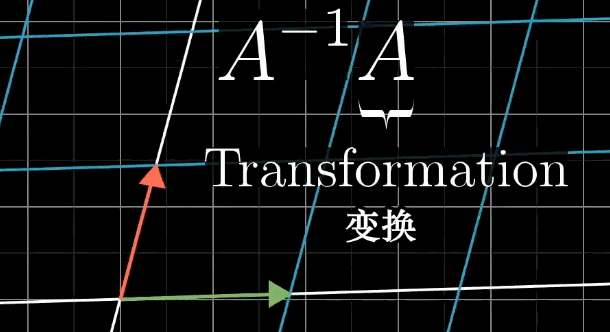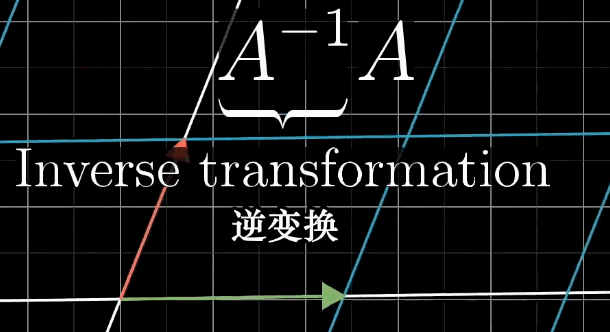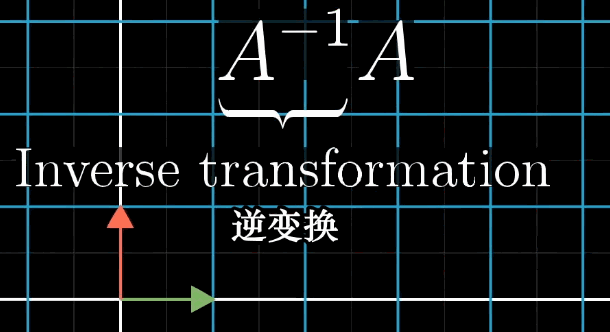
6.2.2 线性方程组的解
在线性代数中,任意一个 m × n m \times n m×n 型线性方程组均可以表示为矩阵形式 A x = v A\mathbf{x} = \mathbf{v} Ax=v,其中各符号的定义如下:
- A ∈ R m × n A \in \mathbb{R}^{m \times n} A∈Rm×n:称为系数矩阵,由方程组中未知量的系数按原顺序构成;
- x ∈ R n \mathbf{x} \in \mathbb{R}^n x∈Rn:称为未知向量,包含方程组中所有待求解的未知量;
- v ∈ R m \mathbf{v} \in \mathbb{R}^m v∈Rm:称为常数项向量,由方程组等号右侧的常数项构成。
该矩阵形式的核心意义在于:线性方程组 A x = v A\mathbf{x} = \mathbf{v} Ax=v 与从向量空间 R n \mathbb{R}^n Rn 到 R m \mathbb{R}^m Rm 的线性变换 T A : R n → R m T_A: \mathbb{R}^n \to \mathbb{R}^m TA:Rn→Rm(定义为 T A ( x ) = A x T_A(\mathbf{x}) = A\mathbf{x} TA(x)=Ax)一一对应。这种对应关系将“求解方程组”转化为“分析线性变换的性质”,我们可从逆变换、列空间、零空间三个维度,系统讨论方程组解的存在性、唯一性及解集合的结构。
1. 逆变换与方程组的唯一解
当线性变换 T A T_A TA 满足“可逆”条件时,方程组 A x = v A\mathbf{x} = \mathbf{v} Ax=v 存在唯一解,具体推导与结论如下:
1.1 可逆的等价条件
线性变换 T A T_A TA 可逆,等价于其对应的系数矩阵 A A A 满足两个条件:
- A A A 是方阵(即 m = n m = n m=n,方程组的“方程个数”等于“未知量个数”);
- A A A 的行列式非零(即 det ( A ) ≠ 0 \det(A) \neq 0 det(A)=0,此时 A A A 称为可逆矩阵或非奇异矩阵)。
行列式非零的几何意义是:线性变换 T A T_A TA 不会导致向量空间“降维”(例如, R 3 \mathbb{R}^3 R3 中的变换不会将向量映射到 R 2 \mathbb{R}^2 R2 或更低维的空间),因此每个输出向量 v \mathbf{v} v 都能唯一对应一个输入向量 x \mathbf{x} x。
1.2 唯一解的代数形式
若
A
A
A 可逆,则其逆矩阵
A
−
1
A^{-1}
A−1 存在且唯一(满足
A
−
1
A
=
A
A
−
1
=
I
A^{-1}A = AA^{-1} = I
A−1A=AA−1=I,其中
I
I
I 为单位矩阵)。对
A
x
=
v
A\mathbf{x} = \mathbf{v}
Ax=v 两边同时左乘
A
−
1
A^{-1}
A−1,可通过矩阵运算直接求解
x
\mathbf{x}
x:
A
−
1
A
x
=
A
−
1
v
⟹
I
x
=
A
−
1
v
⟹
x
=
A
−
1
v
A^{-1}A\mathbf{x} = A^{-1}\mathbf{v} \implies I\mathbf{x} = A^{-1}\mathbf{v} \implies \mathbf{x} = A^{-1}\mathbf{v}
A−1Ax=A−1v⟹Ix=A−1v⟹x=A−1v
从线性变换的角度看,该解等价于“将逆变换
T
A
−
1
T_A^{-1}
TA−1 作用于
v
\mathbf{v}
v”,即
x
=
T
A
−
1
(
v
)
\mathbf{x} = T_A^{-1}(\mathbf{v})
x=TA−1(v),这进一步印证了解的唯一性——逆变换的输出是唯一的。
2. 列空间与方程组的解的存在性
当 T A T_A TA 不可逆(或 A A A 非方阵)时,方程组 A x = v A\mathbf{x} = \mathbf{v} Ax=v 未必有解,需通过系数矩阵 A A A 的列空间(Column Space)判定解的存在性。
2.1 列空间的定义
系数矩阵
A
A
A 的列空间(记为
Col
(
A
)
\text{Col}(A)
Col(A))是
A
A
A 的所有列向量在
R
m
\mathbb{R}^m
Rm 中通过“线性组合”张成的子空间。例如,若
A
=
[
a
1
a
2
…
a
n
]
A = [\mathbf{a}_1\ \mathbf{a}_2\ \dots\ \mathbf{a}_n]
A=[a1 a2 … an](其中
a
i
∈
R
m
\mathbf{a}_i \in \mathbb{R}^m
ai∈Rm 是
A
A
A 的第
i
i
i 列),则:
Col
(
A
)
=
{
c
1
a
1
+
c
2
a
2
+
⋯
+
c
n
a
n
∣
c
1
,
c
2
,
…
,
c
n
∈
R
}
\text{Col}(A) = \left\{ c_1\mathbf{a}_1 + c_2\mathbf{a}_2 + \dots + c_n\mathbf{a}_n \mid c_1, c_2, \dots, c_n \in \mathbb{R} \right\}
Col(A)={c1a1+c2a2+⋯+cnan∣c1,c2,…,cn∈R}
其几何意义是:线性变换
T
A
T_A
TA 的所有可能输出向量构成的集合,即
T
A
T_A
TA 的“值域”。
2.2 解的存在性充要条件
根据列空间的定义,方程组 A x = v A\mathbf{x} = \mathbf{v} Ax=v 有解的本质是“ v \mathbf{v} v 属于 T A T_A TA 的值域”,因此可得到核心结论:
线性方程组 A x = v A\mathbf{x} = \mathbf{v} Ax=v 有解的充要条件是:常数项向量 v \mathbf{v} v 属于系数矩阵 A A A 的列空间,即 v ∈ Col ( A ) \mathbf{v} \in \text{Col}(A) v∈Col(A)。
结合行列式的特殊情况(当 A A A 为方阵时):
- 若 det ( A ) ≠ 0 \det(A) \neq 0 det(A)=0( A A A 可逆),则 Col ( A ) = R m \text{Col}(A) = \mathbb{R}^m Col(A)=Rm(列空间充满整个目标空间),因此对任意 v ∈ R m \mathbf{v} \in \mathbb{R}^m v∈Rm,方程组均有解(与第1节结论一致);
- 若 det ( A ) = 0 \det(A) = 0 det(A)=0( A A A 不可逆),则 Col ( A ) \text{Col}(A) Col(A) 是 R m \mathbb{R}^m Rm 的真子空间(维度低于 m m m),此时仅当 v \mathbf{v} v 落在该真子空间内时,方程组有解,否则无解。
3. 零空间与方程组的解集合结构
当方程组 A x = v A\mathbf{x} = \mathbf{v} Ax=v 有解时,解的个数可能是“唯一”或“无穷多”,需通过系数矩阵 A A A 的零空间(Null Space)刻画解集合的完整结构。
3.1 零空间的定义
系数矩阵
A
A
A 的零空间(记为
Nul
(
A
)
\text{Nul}(A)
Nul(A))是齐次线性方程组
A
x
=
0
A\mathbf{x} = \mathbf{0}
Ax=0(常数项向量全为0的方程组)的所有解向量在
R
n
\mathbb{R}^n
Rn 中构成的子空间,即:
Nul
(
A
)
=
{
z
∈
R
n
∣
A
z
=
0
}
\text{Nul}(A) = \left\{ \mathbf{z} \in \mathbb{R}^n \mid A\mathbf{z} = \mathbf{0} \right\}
Nul(A)={z∈Rn∣Az=0}
齐次方程组
A
x
=
0
A\mathbf{x} = \mathbf{0}
Ax=0 始终有解(至少存在零解
x
=
0
\mathbf{x} = \mathbf{0}
x=0),因此零空间
Nul
(
A
)
\text{Nul}(A)
Nul(A) 永远非空。
3.2 解集合的结构定理
设非齐次方程组
A
x
=
v
A\mathbf{x} = \mathbf{v}
Ax=v 有解,且
x
0
\mathbf{x}_0
x0 是其任意一个特解(即满足
A
x
0
=
v
A\mathbf{x}_0 = \mathbf{v}
Ax0=v 的某个固定解),则方程组的所有解可表示为“特解 + 零空间中任意向量”的形式,即:
x
=
x
0
+
z
,
其中
z
∈
Nul
(
A
)
\mathbf{x} = \mathbf{x}_0 + \mathbf{z}, \quad \text{其中 } \mathbf{z} \in \text{Nul}(A)
x=x0+z,其中 z∈Nul(A)
该定理的逻辑验证如下:
-
解的有效性:若 z ∈ Nul ( A ) \mathbf{z} \in \text{Nul}(A) z∈Nul(A),则 A z = 0 A\mathbf{z} = \mathbf{0} Az=0,因此 A ( x 0 + z ) = A x 0 + A z = v + 0 = v A(\mathbf{x}_0 + \mathbf{z}) = A\mathbf{x}_0 + A\mathbf{z} = \mathbf{v} + \mathbf{0} = \mathbf{v} A(x0+z)=Ax0+Az=v+0=v,即 x 0 + z \mathbf{x}_0 + \mathbf{z} x0+z 是方程组的解;
-
解的完整性:设 x \mathbf{x} x 是方程组的任意一个解,则 A ( x − x 0 ) = A x − A x 0 = v − v = 0 A(\mathbf{x} - \mathbf{x}_0) = A\mathbf{x} - A\mathbf{x}_0 = \mathbf{v} - \mathbf{v} = \mathbf{0} A(x−x0)=Ax−Ax0=v−v=0,即 x − z ∈ Nul ( A ) \mathbf{x} - \mathbf{z} \in \text{Nul}(A) x−z∈Nul(A),因此 x \mathbf{x} x 可表示为 x 0 + ( x − x 0 ) \mathbf{x}_0 + (\mathbf{x} - \mathbf{x}_0) x0+(x−x0),符合上述形式。
3.3 特殊情况的解集合
根据上述定理,可进一步明确两类典型方程组的解集合:
- 非齐次方程组
A
x
=
v
A\mathbf{x} = \mathbf{v}
Ax=v:
- 若 v ∉ Col ( A ) \mathbf{v} \notin \text{Col}(A) v∈/Col(A):解集合为空集(无解);
- 若 v ∈ Col ( A ) \mathbf{v} \in \text{Col}(A) v∈Col(A):解集合为 { x 0 + z ∣ z ∈ Nul ( A ) } \left\{ \mathbf{x}_0 + \mathbf{z} \mid \mathbf{z} \in \text{Nul}(A) \right\} {x0+z∣z∈Nul(A)}(无穷多解,除非 Nul ( A ) = { 0 } \text{Nul}(A) = \left\{ \mathbf{0} \right\} Nul(A)={0},即零空间仅含零向量,此时解唯一)。
- 齐次方程组
A
x
=
0
A\mathbf{x} = \mathbf{0}
Ax=0:
- 特解 x 0 = 0 \mathbf{x}_0 = \mathbf{0} x0=0(零解),因此解集合就是零空间 Nul ( A ) \text{Nul}(A) Nul(A);
- 若 Nul ( A ) = { 0 } \text{Nul}(A) = \left\{ \mathbf{0} \right\} Nul(A)={0},则仅有零解;若 Nul ( A ) \text{Nul}(A) Nul(A) 维度大于0,则有无穷多非零解。
6.3 列空间(Column Space)
矩阵 A A A 的列空间是其所有列向量张成的空间,记为 C ( A ) C (A) C(A)。
- 几何意义:列空间是线性变换 A A A 的 “所有可能输出向量” 的集合(即 A x ⃗ A\vec {x} Ax 的所有可能结果);
- 维度与秩:列空间的维度称为矩阵的秩(记为 rank ( A ) \text {rank}(A) rank(A))。对于 n × n n \times n n×n 矩阵,若 rank ( A ) = n \text {rank}(A) = n rank(A)=n(满秩),则列空间是整个 n n n 维空间;若 rank ( A ) < n \text {rank}(A) < n rank(A)<n(降秩),则列空间是 n n n 维空间的一个子空间(如二维中的直线、三维中的平面)。

重要性质:零向量 0 ⃗ \vec {0} 0 一定在列空间中(令 x ⃗ = 0 ⃗ \vec {x} = \vec {0} x=0,则 A 0 ⃗ = 0 ⃗ A\vec {0} = \vec {0} A0=0)。
6.4 零空间(Null Space)
所有经过该矩阵变换后落在原点的向量的集合,称为该矩阵(再次强调,矩阵是变换的数字表达)的零空间或核。
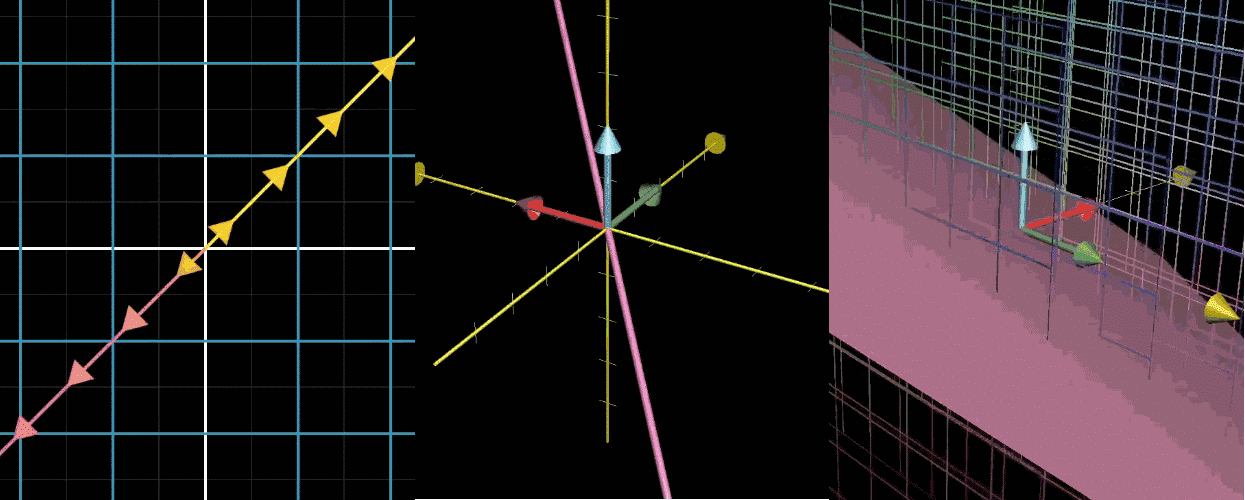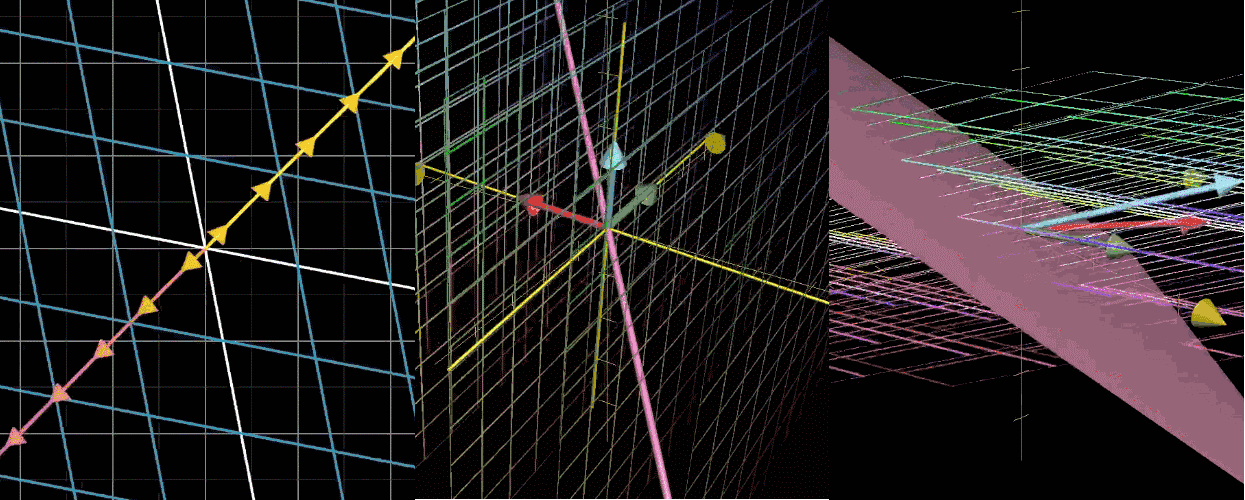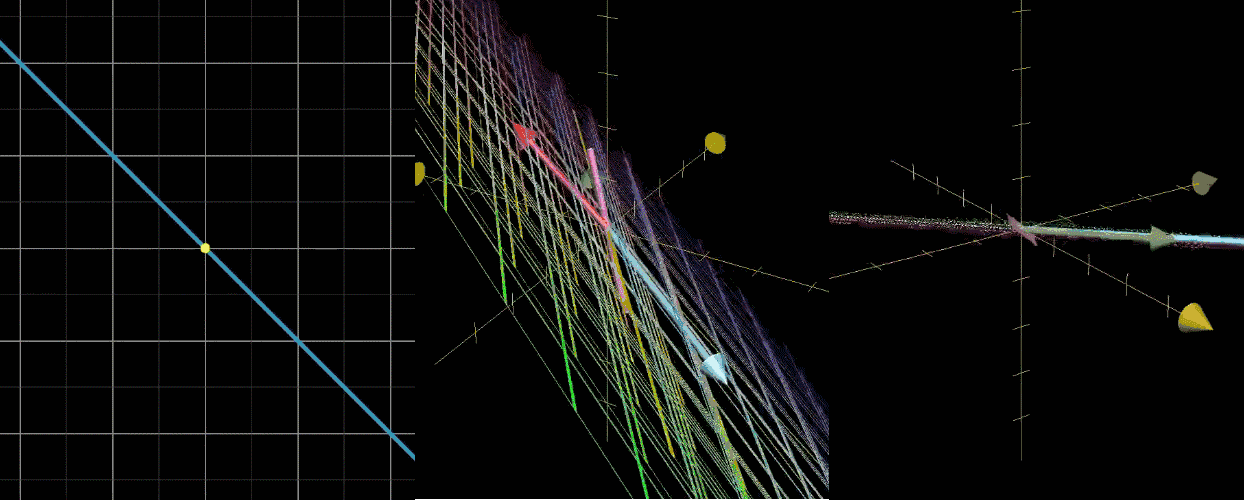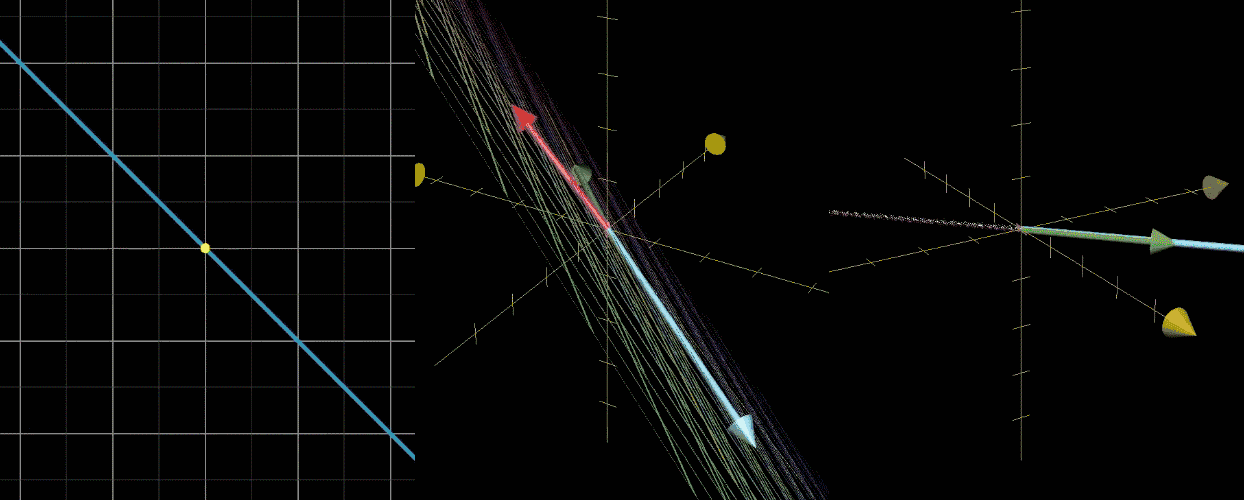
图 1 二维空间压缩到一条直线(一维),其中一条直线(一维)上的点被压缩到原点。
图 2 三维空间压缩到一个平面(二维),其中一条直线(一维)上的点被压缩到原点。
图 3 三维空间压缩到一条直线(一维),其中一个平面(二维)上的点被压缩到原点。
注意: 线性压缩是一种线性变换,而矩阵是线性变换在给定基下的代数表示(数字表达),二者一一对应但并非等同。
矩阵 A A A 的零空间是满足 A x ⃗ = 0 ⃗ A\vec {x} = \vec {0} Ax=0 的所有向量 x ⃗ \vec {x} x 的集合,记为 N ( A ) N (A) N(A)。
- 几何意义:零空间是线性变换 A A A 中 “被压缩到原点的向量” 的集合;
- 维度关系(秩 - 零定理):对于 n × n n \times n n×n 矩阵, rank ( A ) + dim ( N ( A ) ) = n \text {rank}(A) + \dim (N (A)) = n rank(A)+dim(N(A))=n(列空间维度与零空间维度之和等于矩阵的阶数)。
示例:
- 若 A A A 是 2 × 2 2 \times 2 2×2 矩阵且 det ( A ) = 0 \det (A) = 0 det(A)=0(二维→一维),则零空间是一条直线(所有被压缩到原点的向量构成的直线);
- 若 A A A 是 3 × 3 3 \times 3 3×3 矩阵且 rank ( A ) = 2 \text {rank}(A) = 2 rank(A)=2(三维→二维),则零空间是一条直线( dim ( N ( A ) ) = 3 − 2 = 1 \dim (N (A)) = 3 - 2 = 1 dim(N(A))=3−2=1)。
6.4.1 秩-零化度定理
零化度(Nullity)是线性代数中矩阵零空间的维数,是衡量矩阵“将向量映射为零向量”能力的重要指标。
- 零空间(Null Space,又称核空间 Kernel):指矩阵 A ∈ R m × n A \in \mathbb{R}^{m \times n} A∈Rm×n 的所有解向量 x ∈ R n \mathbf{x} \in \mathbb{R}^n x∈Rn 的集合,即 N ( A ) = { x ∈ R n ∣ A x = 0 } \text{N}(A) = \{\mathbf{x} \in \mathbb{R}^n \mid A\mathbf{x} = \mathbf{0}\} N(A)={x∈Rn∣Ax=0}。
- 零化度的本质:零空间作为一个向量空间,其维数即为零化度(记为 nullity ( A ) \text{nullity}(A) nullity(A)),等价于零空间中“极大线性无关组的向量个数”(即零空间的基向量数)。
- 零化度的计算:通过对矩阵 A A A 做初等行变换化为行最简形,解线性方程组 A x = 0 A\mathbf{x} = \mathbf{0} Ax=0 得到自由变量的个数,该个数即为零化度(自由变量数 = 零空间维数)。
对任意 m × n m \times n m×n 矩阵 A A A,其列空间的维数(即秩 rank ( A ) \text{rank}(A) rank(A))与零空间的维数(零化度)之和,等于矩阵的列数 n n n,即:
dim ( Col ( A ) ) + dim ( Nul ( A ) ) = n \dim(\text{Col}(A)) + \dim(\text{Nul}(A)) = n dim(Col(A))+dim(Nul(A))=n
注意:是“维数之和”,而非“空间本身相加”——列空间( R m \mathbb{R}^m Rm 子空间)与零空间( R n \mathbb{R}^n Rn 子空间)维度可能不同,无法直接叠加。
6.4.2 满秩与列空间、零空间
“满秩”是矩阵的属性( rank ( A ) = min ( m , n ) \text{rank}(A) = \min(m, n) rank(A)=min(m,n)),结合上述定理分析:
- 若
A
A
A 为
n
×
n
n \times n
n×n 方阵(满秩即
rank
(
A
)
=
n
\text{rank}(A) = n
rank(A)=n):
由定理得 dim ( Nul ( A ) ) = 0 \dim(\text{Nul}(A)) = 0 dim(Nul(A))=0(零空间仅含零向量),且列空间 Col ( A ) = R n \text{Col}(A) = \mathbb{R}^n Col(A)=Rn(满维子空间)。 - 若
A
A
A 为长方阵(如
m
<
n
m < n
m<n 时满秩即
rank
(
A
)
=
m
\text{rank}(A) = m
rank(A)=m):
列空间 Col ( A ) = R m \text{Col}(A) = \mathbb{R}^m Col(A)=Rm(满维),零空间维数 n − m > 0 n - m > 0 n−m>0(含非零解)。
7 非方阵的几何意义
On this quiz, I asked you to find the determinant of a 2*3 matrix. Some of you, to my great amusement, actually tried to do this - no name listed
在这个小测试里,我让你们求一个 2*3 矩阵的行列式。让我感到非常可笑的是,你们当中竟然有人尝试去做 ——佚名
7.1 非方阵的维度映射
非方阵(如 m × n m \times n m×n 矩阵, m ≠ n m \neq n m=n)对应的线性变换是不同维度空间之间的映射:
- m × n m \times n m×n 矩阵:将 n n n 维输入空间映射到 m m m 维输出空间;
- 示例: 3 × 2 3 \times 2 3×2 矩阵将二维空间映射到三维空间(输入为 2 2 2 维向量,输出为 3 3 3 维向量),其列向量是二维标准基 { ı ^ , ȷ ^ } \{\hat {\imath}, \hat {\jmath}\} {^,^} 在三维空间中的变换结果。
7.2 非方阵乘法的条件
两个非方阵 M 1 M_1 M1( p × q p \times q p×q)与 M 2 M_2 M2( q × r q \times r q×r)可相乘的充要条件是:前一个矩阵的列数等于后一个矩阵的行数(即 M 1 M_1 M1 的输入维度等于 M 2 M_2 M2 的输出维度),乘积矩阵 M = M 1 M 2 M = M_1M_2 M=M1M2 的维度为 p × r p \times r p×r。
- 几何意义: M 2 M_2 M2 将 r r r 维空间映射到 q q q 维空间, M 1 M_1 M1 再将 q q q 维空间映射到 p p p 维空间,复合变换的输入维度为 r r r,输出维度为 p p p,与乘积矩阵维度一致。
7.3 非方阵的行列式
非方阵不存在行列式,因为行列式的核心是 “体积缩放比例”,而不同维度空间之间的映射(如二维→三维)无法定义 “体积比”(二维空间的 “面积” 与三维空间的 “体积” 单位不同,无直接比例关系)。
8 点积与对偶性
卡尔文:你知道吗,我觉数学不是一门科学,而是一种宗教。
霍布斯:一种宗教?
卡尔文:是啊。这些公式就像奇迹一般。你取出两个数,把它们相加时,它们神奇地成为了一个全新的数!没人能说清这到底是怎么发生的。你要么完全相信,要么完全不信。
8.1 点积的定义与几何意义
8.1.1 代数定义
对于
n
n
n 维向量
v
⃗
=
[
v
1
v
2
⋯
v
n
]
\vec {v} = \begin {bmatrix} v_1 \\ v_2 \\ \cdots \\ v_n \end {bmatrix}
v=
v1v2⋯vn
与
w
⃗
=
[
w
1
w
2
⋯
w
n
]
\vec {w} = \begin {bmatrix} w_1 \\ w_2 \\ \cdots \\ w_n \end {bmatrix}
w=
w1w2⋯wn
,其点积为:
v
⃗
⋅
w
⃗
=
v
1
w
1
+
v
2
w
2
+
⋯
+
v
n
w
n
\vec {v} \cdot \vec {w} = v_1w_1 + v_2w_2 + \cdots + v_nw_n
v⋅w=v1w1+v2w2+⋯+vnwn
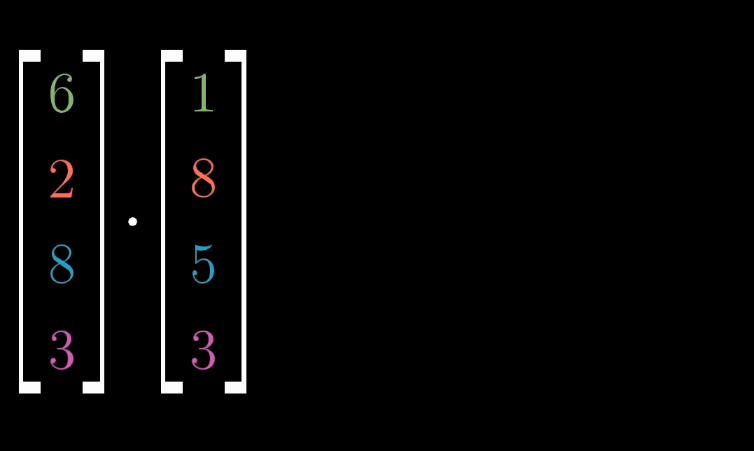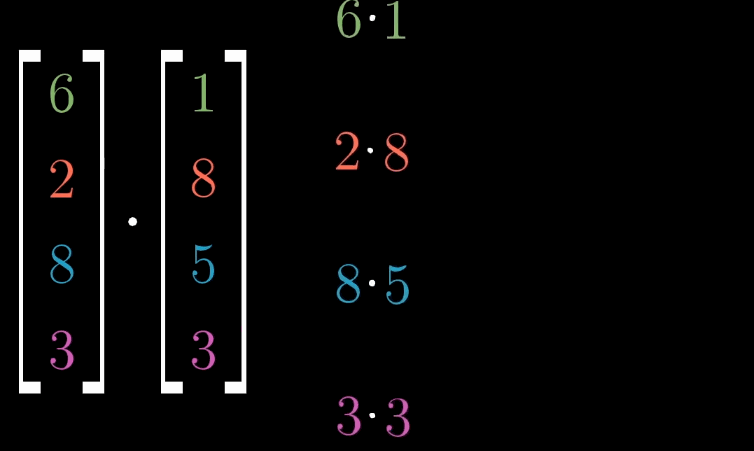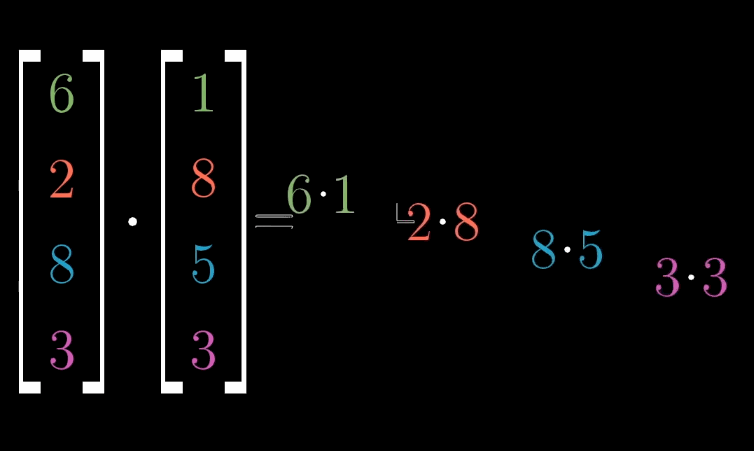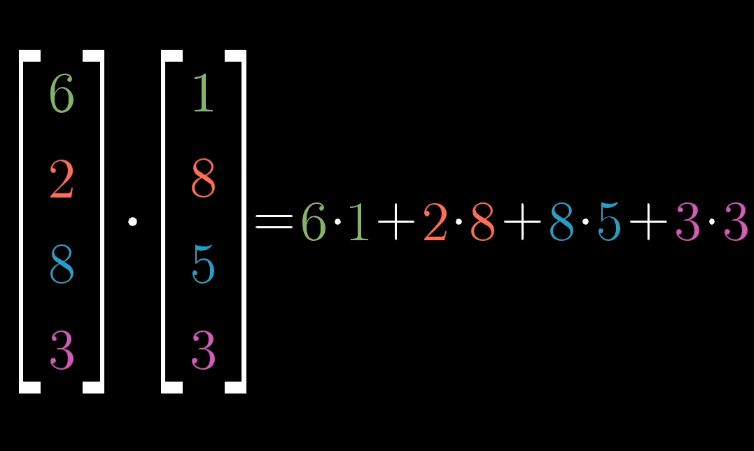
8.1.2 几何意义
点积的几何意义是 “一个向量在另一个向量上的投影长度与被投影向量长度的乘积”,即:
v
⃗
⋅
w
⃗
=
∥
v
⃗
∥
⋅
∥
w
⃗
∥
⋅
cos
θ
\vec {v} \cdot \vec {w} = \|\vec {v}\| \cdot \|\vec {w}\| \cdot \cos\theta
v⋅w=∥v∥⋅∥w∥⋅cosθ
其中
θ
\theta
θ 是
v
⃗
\vec {v}
v 与
w
⃗
\vec {w}
w 的夹角,
∥
v
⃗
∥
=
v
1
2
+
v
2
2
+
⋯
+
v
n
2
\|\vec {v}\| = \sqrt {v_1^2 + v_2^2 + \cdots + v_n^2}
∥v∥=v12+v22+⋯+vn2 是
v
⃗
\vec {v}
v 的长度(模)。
- 符号含义: cos θ > 0 \cos\theta > 0 cosθ>0( θ < 9 0 ∘ \theta < 90^\circ θ<90∘)时,点积为正; cos θ < 0 \cos\theta < 0 cosθ<0( θ > 9 0 ∘ \theta > 90^\circ θ>90∘)时,点积为负; cos θ = 0 \cos\theta = 0 cosθ=0( θ = 9 0 ∘ \theta = 90^\circ θ=90∘)时,点积为 0 0 0(两向量垂直)。
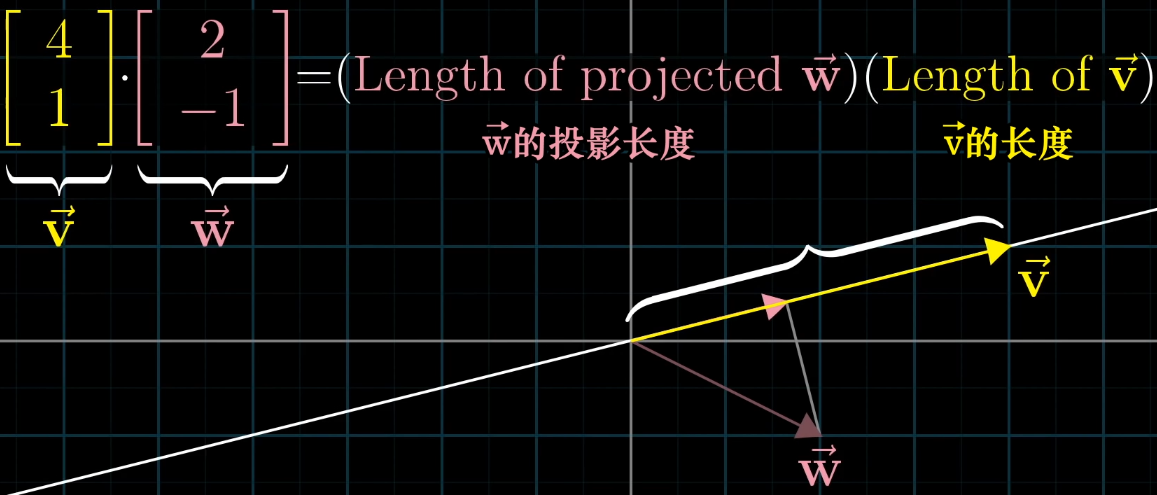
8.2 点积的交换律
点积满足交换律: v ⃗ ⋅ w ⃗ = w ⃗ ⋅ v ⃗ \vec {v} \cdot \vec {w} = \vec {w} \cdot \vec {v} v⋅w=w⋅v,几何解释如下:
- 若 ∥ v ⃗ ∥ = ∥ w ⃗ ∥ \|\vec {v}\| = \|\vec {w}\| ∥v∥=∥w∥,则 v ⃗ \vec {v} v 在 w ⃗ \vec {w} w 上的投影长度等于 w ⃗ \vec {w} w 在 v ⃗ \vec {v} v 上的投影长度,乘积相等;
- 若 ∥ v ⃗ ∥ ≠ ∥ w ⃗ ∥ \|\vec {v}\| \neq \|\vec {w}\| ∥v∥=∥w∥,设 v ⃗ \vec {v} v 的长度为 k ∥ w ⃗ ∥ k\|\vec {w}\| k∥w∥,则 v ⃗ \vec {v} v 在 w ⃗ \vec {w} w 上的投影长度为 k k k 倍 w ⃗ \vec {w} w 在 v ⃗ \vec {v} v 上的投影长度,乘积仍相等(如 v ⃗ = 2 u ⃗ \vec {v} = 2\vec {u} v=2u,则 2 u ⃗ ⋅ w ⃗ = 2 ( u ⃗ ⋅ w ⃗ ) = w ⃗ ⋅ 2 u ⃗ 2\vec {u} \cdot \vec {w} = 2 (\vec {u} \cdot \vec {w}) = \vec {w} \cdot 2\vec {u} 2u⋅w=2(u⋅w)=w⋅2u)。
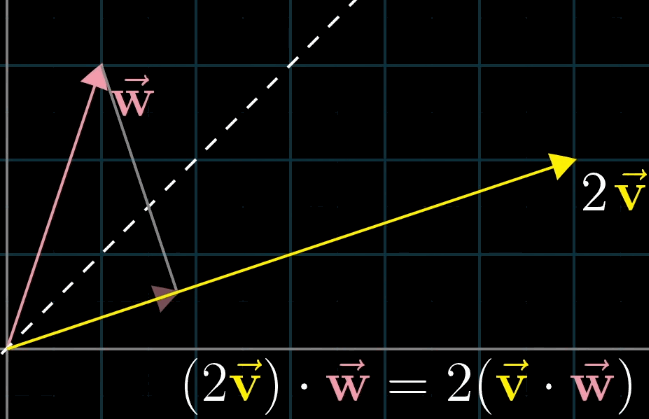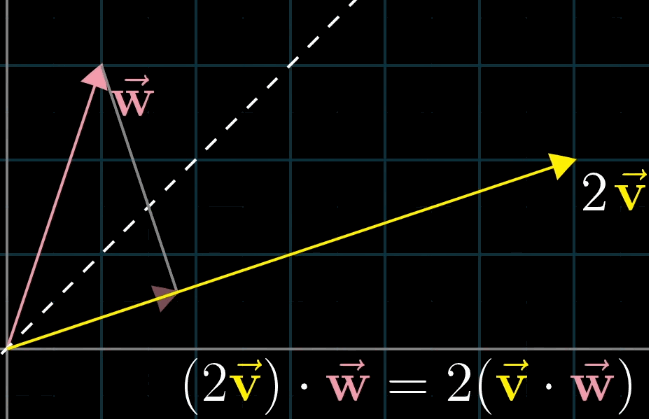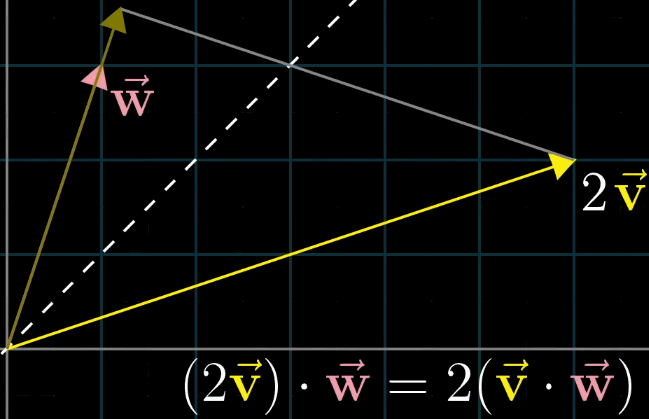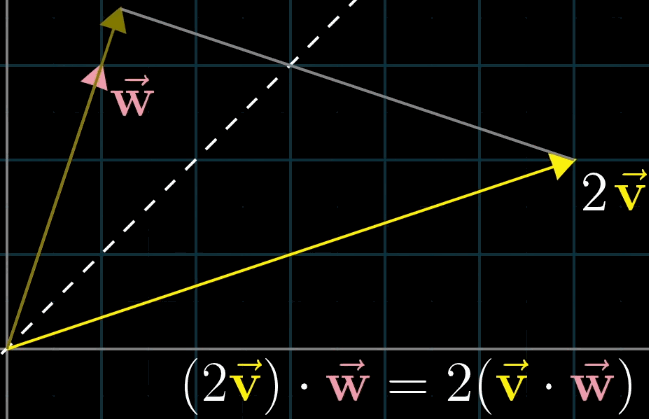
8.3 对偶性:点积与线性变换的对应
8.3.1 多维到一维的线性变换
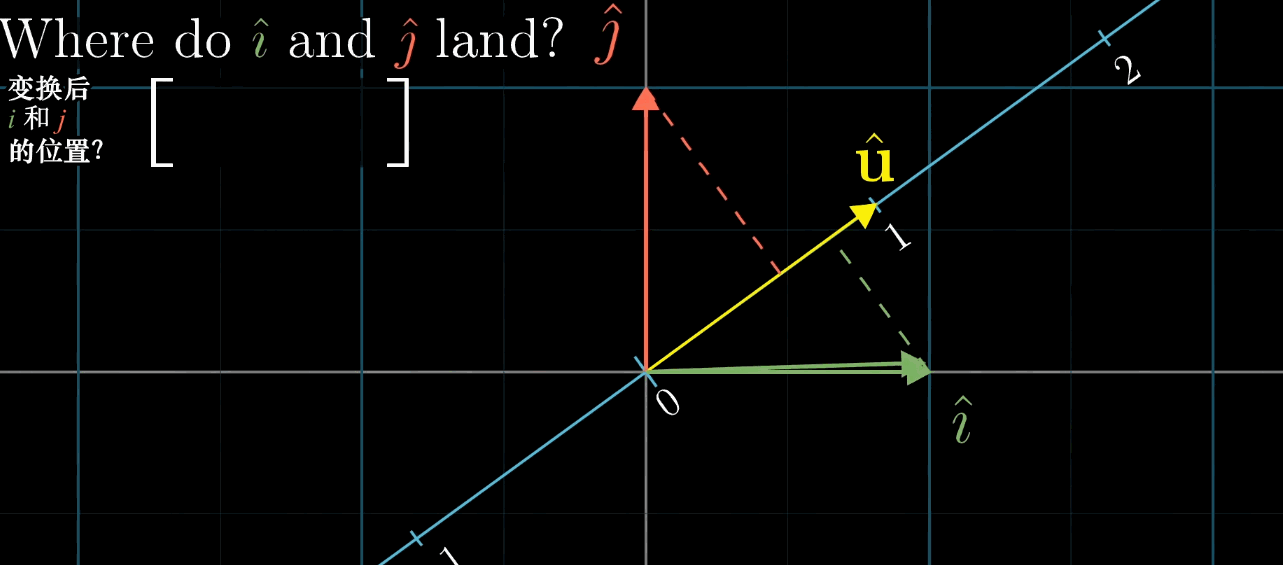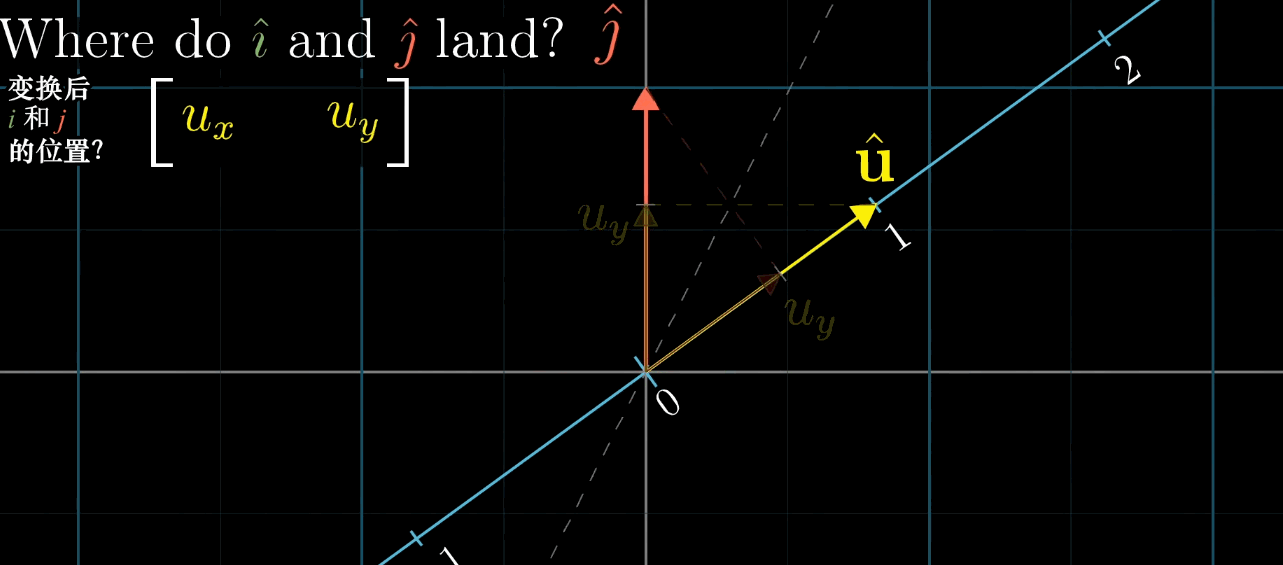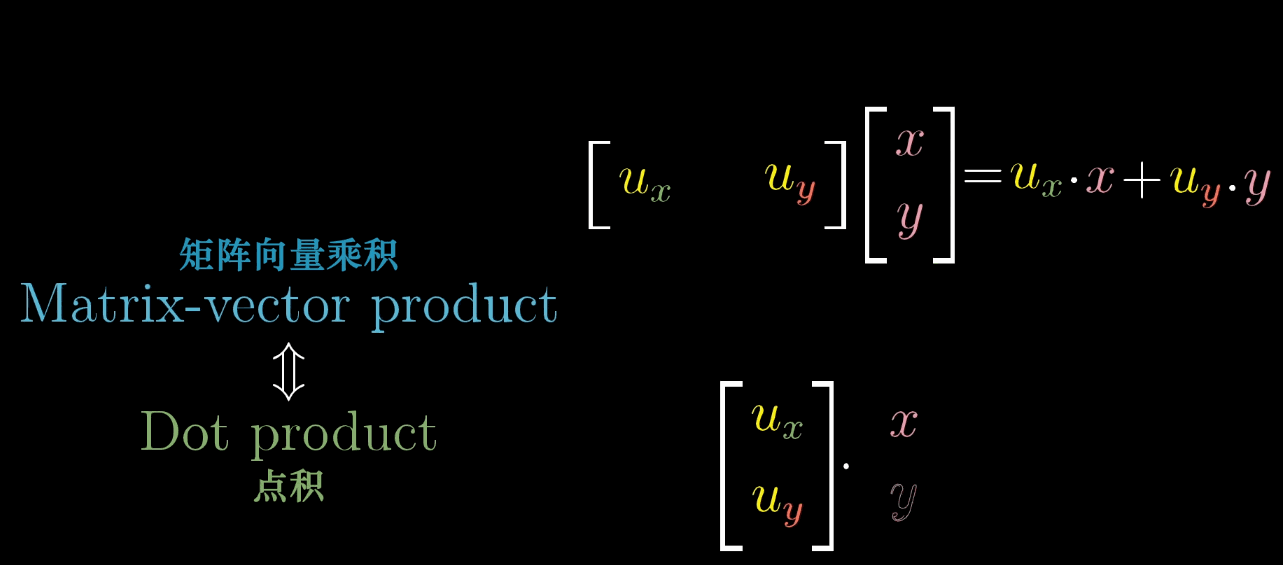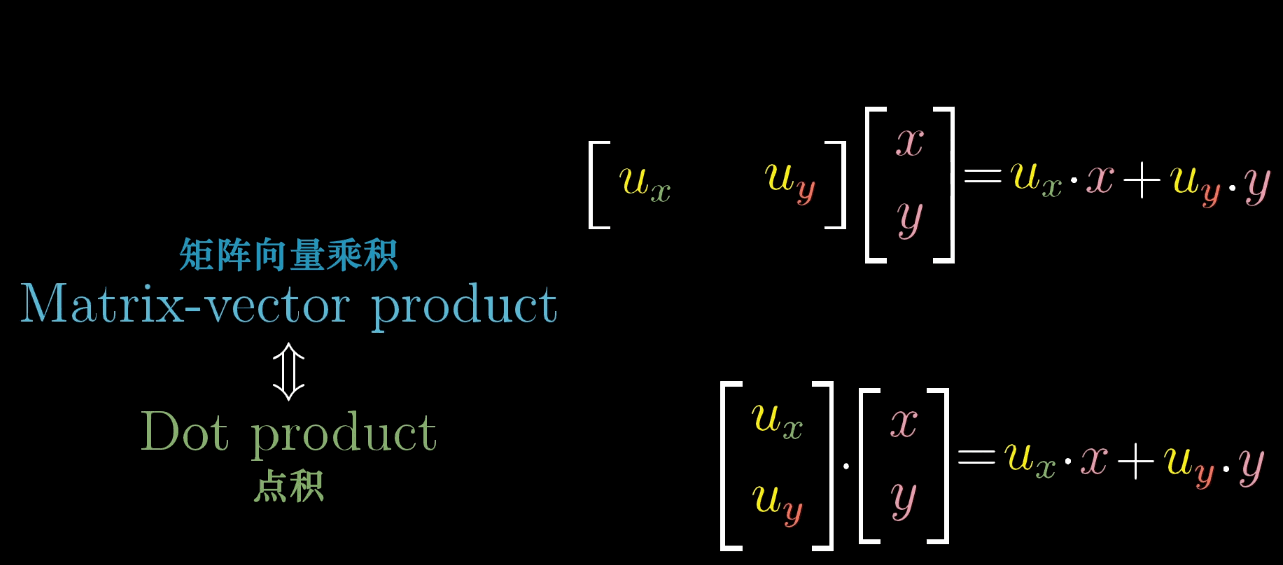
1 × n 1 \times n 1×n 矩阵(行向量)对应的线性变换是将 n n n 维空间映射到一维空间(数轴)。
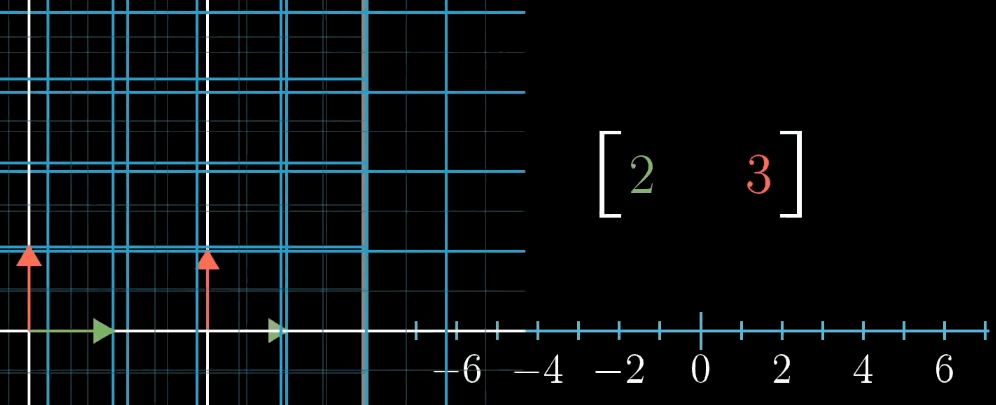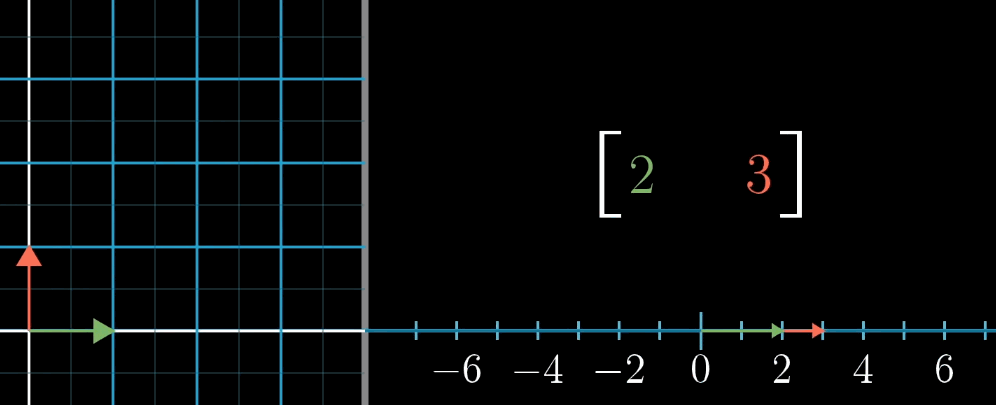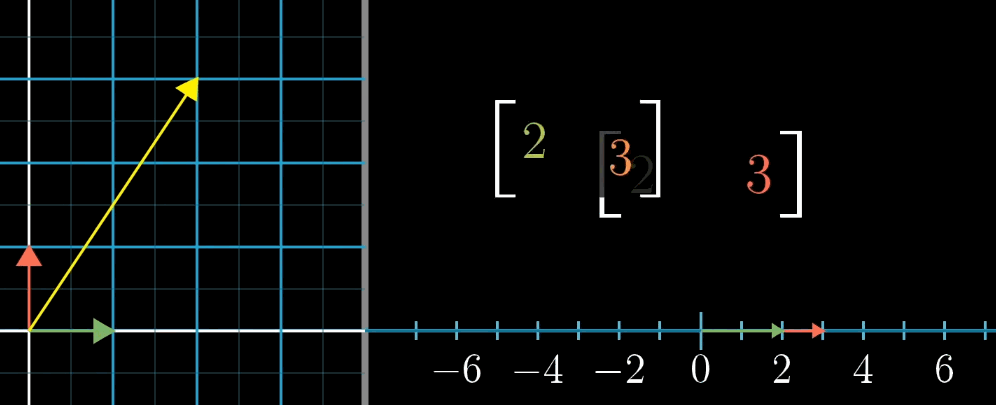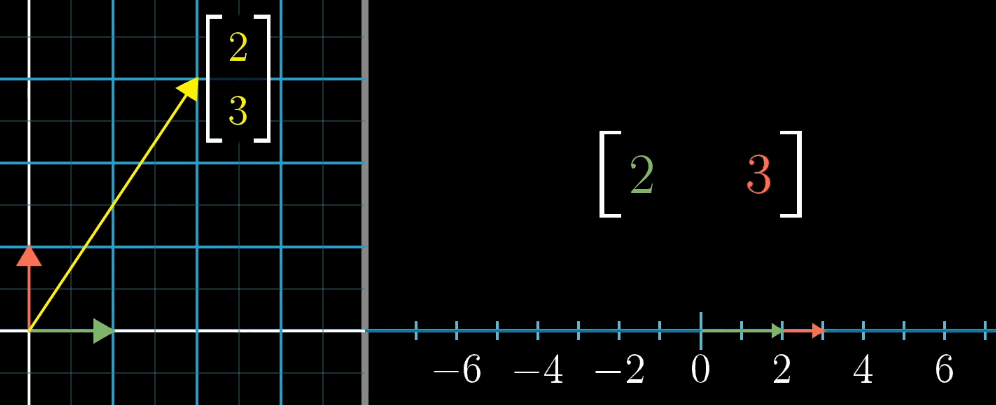
例如, 1 × 2 1 \times 2 1×2 矩阵 [ a b ] \begin {bmatrix} a & b \end {bmatrix} [ab] 对二维向量 [ x y ] \begin {bmatrix} x \\ y \end {bmatrix} [xy] 的变换结果为 a x + b y ax + by ax+by,这与点积 [ a b ] ⋅ [ x y ] \begin {bmatrix} a \\ b \end {bmatrix} \cdot \begin {bmatrix} x \\ y \end {bmatrix} [ab]⋅[xy] 完全一致。
8.3.2 对偶性的定义
对偶性是指 “多维到一维的线性变换” 与 “该空间中的向量” 之间的一一对应关系:
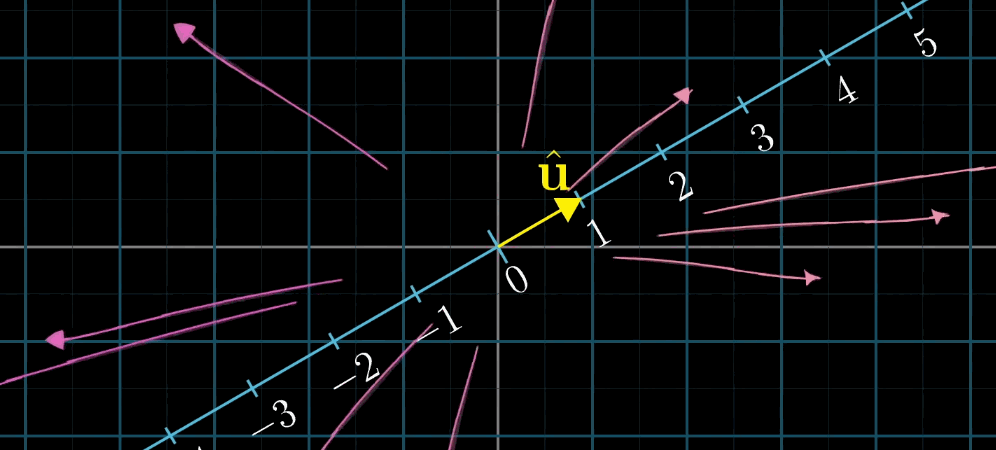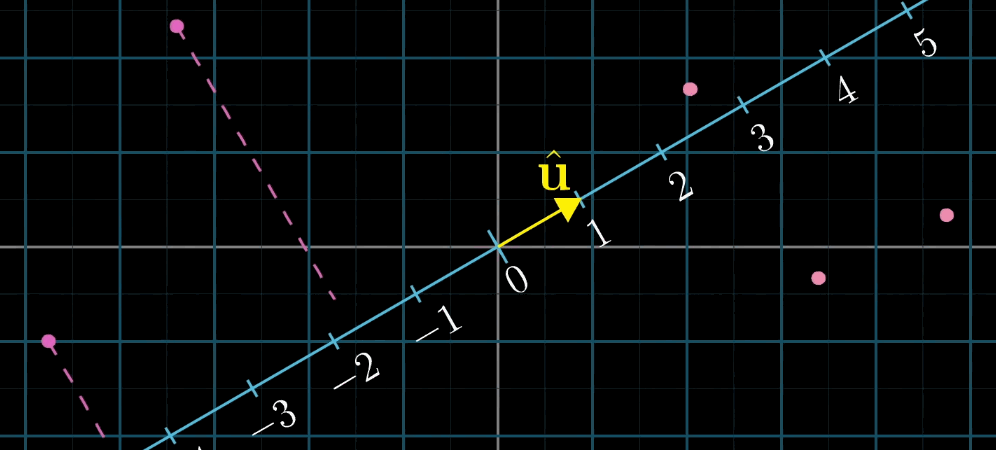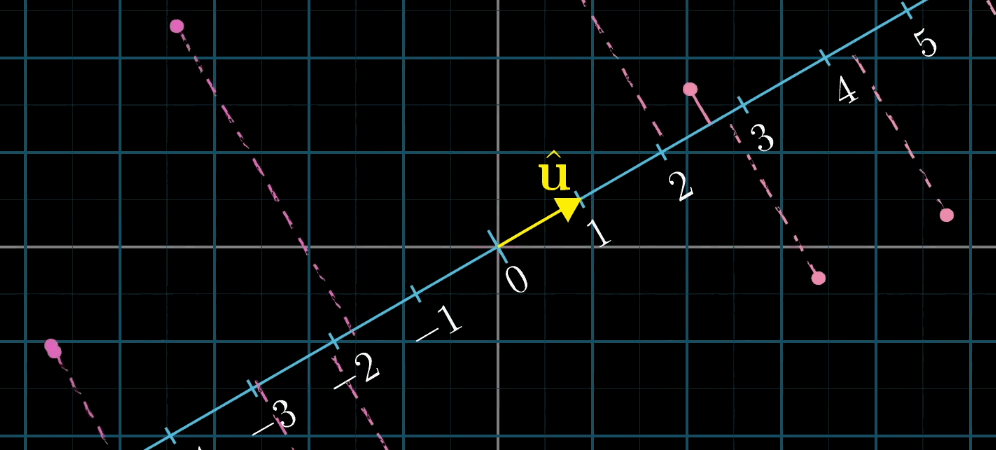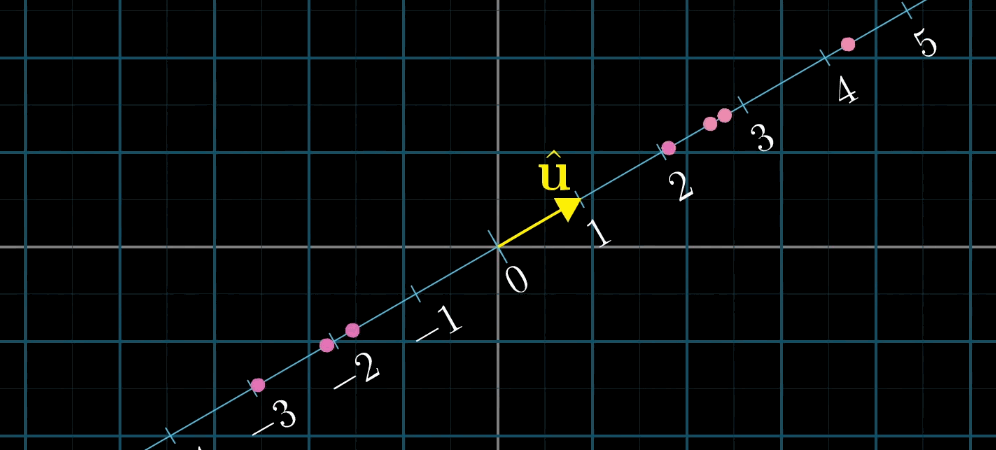
- 对于任意 n n n 维到一维的线性变换 L ( x ⃗ ) L (\vec {x}) L(x),存在唯一的 n n n 维向量 u ⃗ \vec {u} u,使得 L ( x ⃗ ) = u ⃗ ⋅ x ⃗ L (\vec {x}) = \vec {u} \cdot \vec {x} L(x)=u⋅x;
- 反之,任意
n
n
n 维向量
u
⃗
\vec {u}
u 都可定义一个
n
n
n 维到一维的线性变换
L
(
x
⃗
)
=
u
⃗
⋅
x
⃗
L (\vec {x}) = \vec {u} \cdot \vec {x}
L(x)=u⋅x。
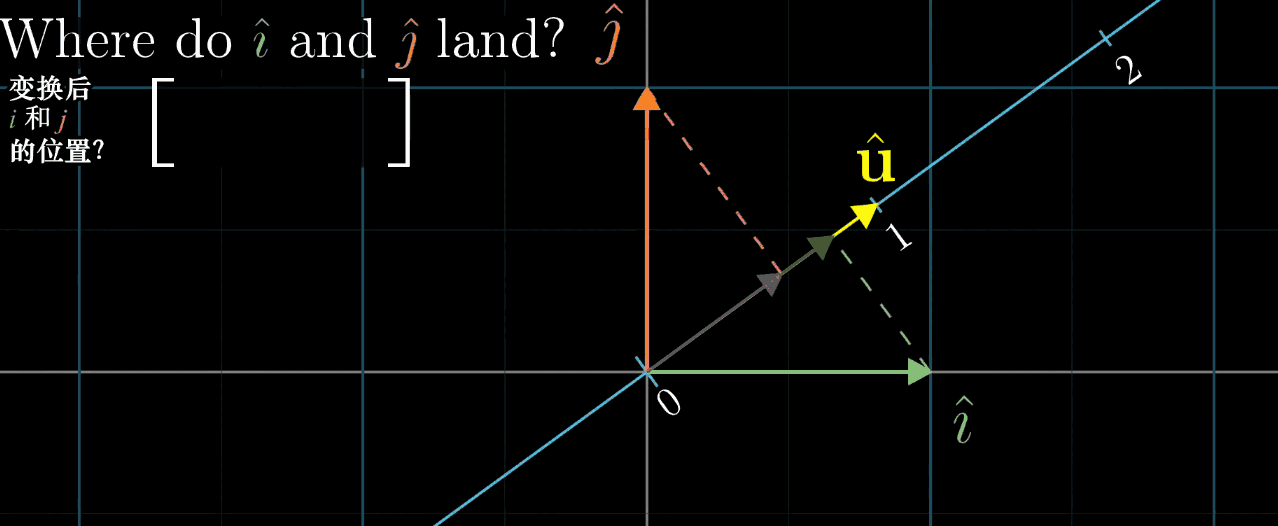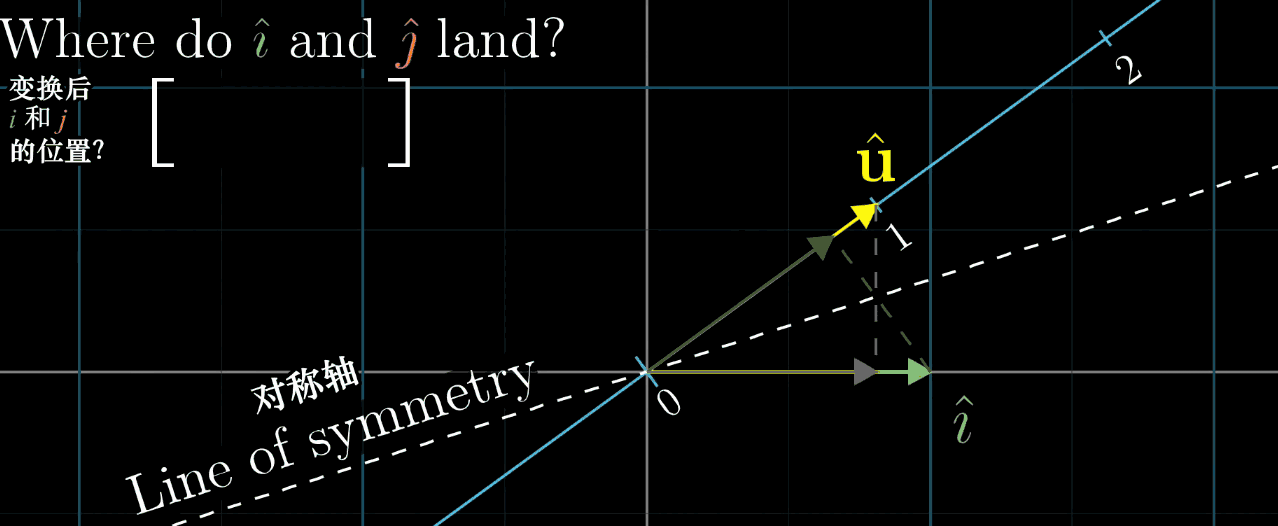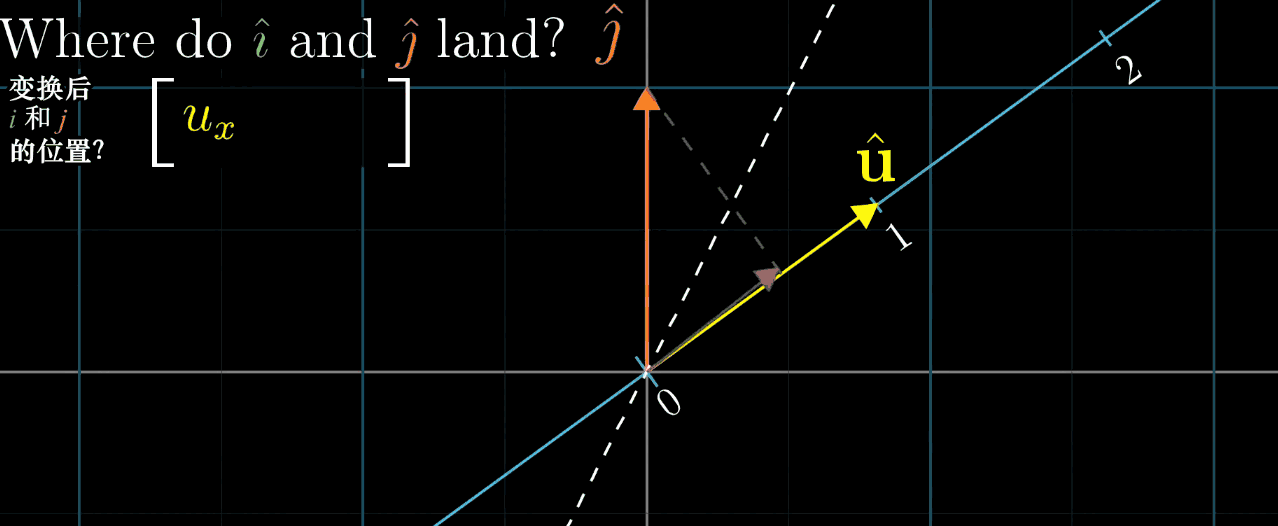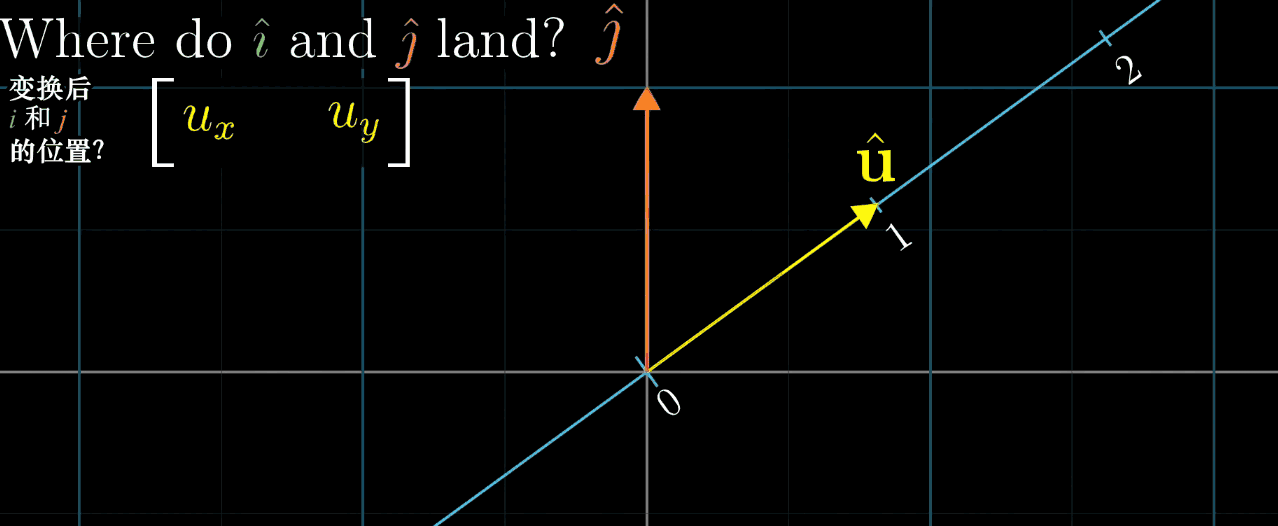
几何解释:设 u ⃗ \vec {u} u 是一维空间(数轴)的单位向量, L ( x ⃗ ) L (\vec {x}) L(x) 是 x ⃗ \vec {x} x 在 u ⃗ \vec {u} u 所在数轴上的投影长度,则 L ( x ⃗ ) = u ⃗ ⋅ x ⃗ L (\vec {x}) = \vec {u} \cdot \vec {x} L(x)=u⋅x(投影长度等于 x ⃗ \vec {x} x 与单位向量 u ⃗ \vec {u} u 的点积)。
9 叉积
每一个维度都很特别。—— 杰弗里・拉加里亚斯(Jeffrey Lagarias)
从他(格罗滕迪克)和他的作为中,我还学到了一点:不以高难度的证明为傲,因为难度高意味着我们还不理解。理想的情况是能够绘出一幅美景,而其中的证明显而易见。
9.1 二维情况下的叉积类比
在二维空间中,向量 v ⃗ \vec{v} v 与 w ⃗ \vec{w} w 张成的平行四边形的面积,可类比为二维 “叉积”(注:严格意义上的叉积仅定义于三维空间,二维情况实为面积的代数值),记为 v ⃗ × w ⃗ \vec{v} \times \vec{w} v×w。
该结果的正负号由基向量 ı ^ \hat{\imath} ^ 和 ȷ ^ \hat{\jmath} ^ 的相对位置关系确定:若 v ⃗ \vec{v} v 与 w ⃗ \vec{w} w 张成的平行四边形中, ȷ ^ \hat{\jmath} ^ 相对于 ı ^ \hat{\imath} ^ 的位置与原始坐标系一致,则结果为正;反之则为负。
结合几何直观,可得出以下结论:
-
向量 v ⃗ \vec{v} v 与 w ⃗ \vec{w} w 的夹角越接近 9 0 ∘ 90^\circ 90∘(垂直),二者张成的平行四边形面积越大;
-
叉积满足分配律,即 v ⃗ × ( w ⃗ 1 + w ⃗ 2 ) = v ⃗ × w ⃗ 1 + v ⃗ × w ⃗ 2 \vec{v} \times (\vec{w}_1 + \vec{w}_2) = \vec{v} \times \vec{w}_1 + \vec{v} \times \vec{w}_2 v×(w1+w2)=v×w1+v×w2。
9.2 真正的叉积定义
严格意义上的叉积定义于三维空间:给定两个三维向量 v ⃗ \vec{v} v 与 w ⃗ \vec{w} w,二者的叉积运算将产生一个新的三维向量 p ⃗ \vec{p} p,且满足以下两个条件:
-
向量 p ⃗ \vec{p} p 的长度等于 v ⃗ \vec{v} v 与 w ⃗ \vec{w} w 张成的平行四边形的面积;
-
向量 p ⃗ \vec{p} p 的方向与 v ⃗ \vec{v} v 和 w ⃗ \vec{w} w 张成的平面垂直,其具体方向由右手定则确定:将右手食指指向 v ⃗ \vec{v} v 的方向,中指指向 w ⃗ \vec{w} w 的方向,此时大拇指所指方向即为 p ⃗ \vec{p} p 的方向。
9.3 叉积计算公式
三维向量叉积的计算公式可通过行列式形式表示,如下所示:
v ⃗ × w ⃗ = [ v 1 v 2 v 3 ] × [ w 1 w 2 w 3 ] = det ( ı ^ v 1 w 1 ȷ ^ v 2 w 2 k ^ v 3 w 3 ) \vec{v} \times \vec{w} = \begin{bmatrix} v_1 \\ v_2 \\ v_3 \end{bmatrix} \times \begin{bmatrix} w_1 \\ w_2 \\ w_3 \end{bmatrix} = \det\begin{pmatrix} \hat{\imath} & v_1 & w_1 \\ \hat{\jmath} & v_2 & w_2 \\ \hat{k} & v_3 & w_3 \end{pmatrix} v×w= v1v2v3 × w1w2w3 =det ^^k^v1v2v3w1w2w3
展开上述行列式,可得:
v ⃗ × w ⃗ = ı ^ ( v 2 w 3 − v 3 w 2 ) − ȷ ^ ( v 1 w 3 − v 3 w 1 ) + k ^ ( v 1 w 2 − v 2 w 1 ) \vec{v} \times \vec{w} = \hat{\imath}(v_2 w_3 - v_3 w_2) - \hat{\jmath}(v_1 w_3 - v_3 w_1) + \hat{k}(v_1 w_2 - v_2 w_1) v×w=^(v2w3−v3w2)−^(v1w3−v3w1)+k^(v1w2−v2w1)
其中, ı ^ \hat{\imath} ^、 ȷ ^ \hat{\jmath} ^、 k ^ \hat{k} k^ 为三维空间的标准单位基向量,这三个基向量前面的系数(即 v 2 w 3 − v 3 w 2 v_2 w_3 - v_3 w_2 v2w3−v3w2、 − ( v 1 w 3 − v 3 w 1 ) -(v_1 w_3 - v_3 w_1) −(v1w3−v3w1)、 v 1 w 2 − v 2 w 1 v_1 w_2 - v_2 w_1 v1w2−v2w1)分别对应叉积结果向量 p ⃗ \vec{p} p 的 x x x、 y y y、 z z z 坐标值。
初次接触该公式时,多数学习者难以理解其形式由来,甚至部分教学过程仅要求记忆公式而不解释逻辑。但基于 “直观理解” 的核心原则,需进一步探明公式的推导过程。
9.4 叉积计算的几何直观
在推导前,需再次强化对偶性的核心概念:每当遇到一个从 “多维空间到数轴” 的线性变换时,该空间中必然存在唯一一个向量与之对应 ——“将线性变换作用于某个向量” 的结果,与 “该向量和对应向量的点积运算” 结果完全等价。
叉积的运算过程正是对偶性的典型实例:根据向量 v ⃗ \vec{v} v 和 w ⃗ \vec{w} w 定义一个从三维空间到数轴的特定线性变换,找到该变换的对偶向量,这个对偶向量即为 v ⃗ \vec{v} v 与 w ⃗ \vec{w} w 的叉积。具体推导步骤如下:
9.4.1 定义线性变换 f ( u ⃗ ) f(\vec{u}) f(u)
已知三维空间中, 3 × 3 3 \times 3 3×3 矩阵的行列式值等于该矩阵三个列向量(或行向量)张成的平行六面体的体积。若将矩阵的第一列替换为自变量向量 u ⃗ = ( x , y , z ) \vec{u} = (x, y, z) u=(x,y,z),后两列固定为向量 v ⃗ \vec{v} v 和 w ⃗ \vec{w} w,则可定义函数:
f ( u ⃗ ) = det ( u ⃗ v ⃗ w ⃗ ) f(\vec{u}) = \det\begin{pmatrix} \vec{u} & \vec{v} & \vec{w} \end{pmatrix} f(u)=det(uvw)
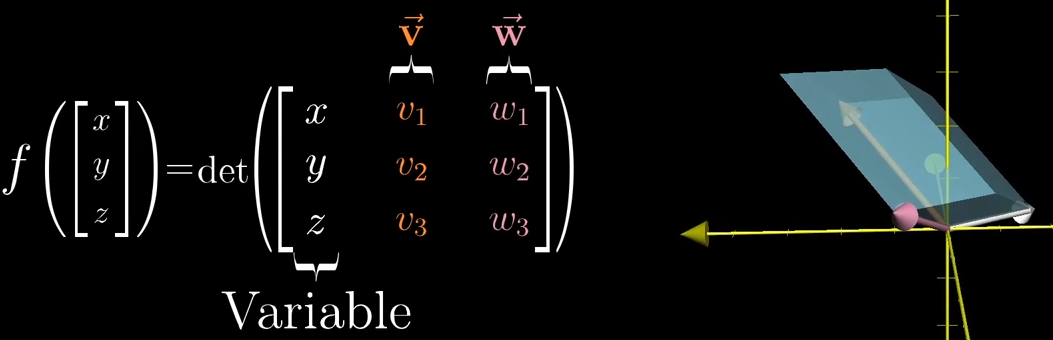
该函数的几何意义为:平行六面体的体积随自变量向量 u ⃗ \vec{u} u 的变化而变化( “平行六面体随白色向量 ( x , y , z ) (x,y,z) (x,y,z) 的随机游走而不断改变” )。此时核心问题转化为:根据 v ⃗ \vec{v} v 和 w ⃗ \vec{w} w,找到一个变换(矩阵或函数),使得上述等式成立。
9.4.2 利用对偶性转化问题
由于 f ( u ⃗ ) f(\vec{u}) f(u) 满足线性变换的 “可加性” 与 “成比例性”(即线性性质),根据对偶性原理,存在一个三维向量 p ⃗ \vec{p} p,使得对任意向量 u ⃗ \vec{u} u,均有:
f ( u ⃗ ) = p ⃗ ⋅ u ⃗ f(\vec{u}) = \vec{p} \cdot \vec{u} f(u)=p⋅u
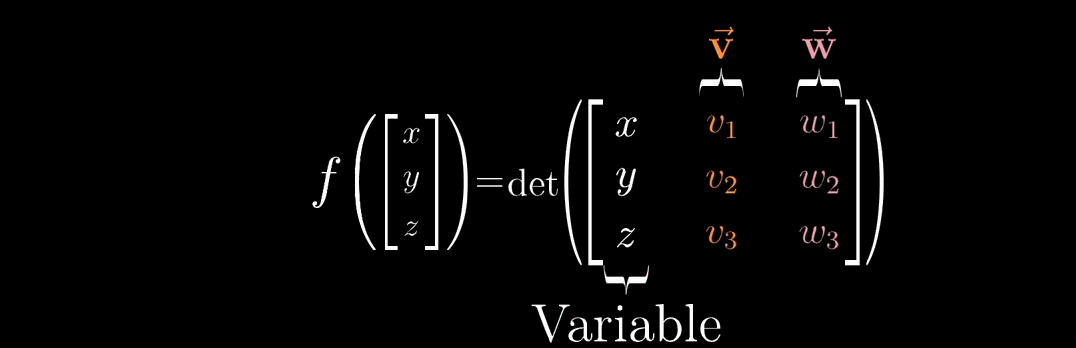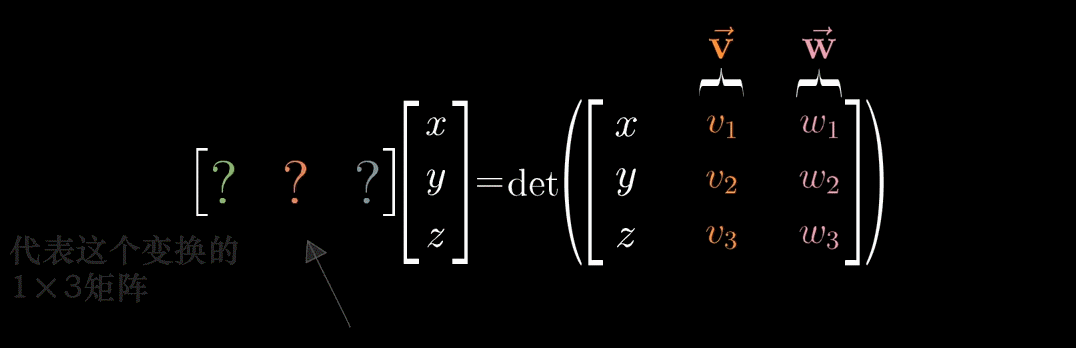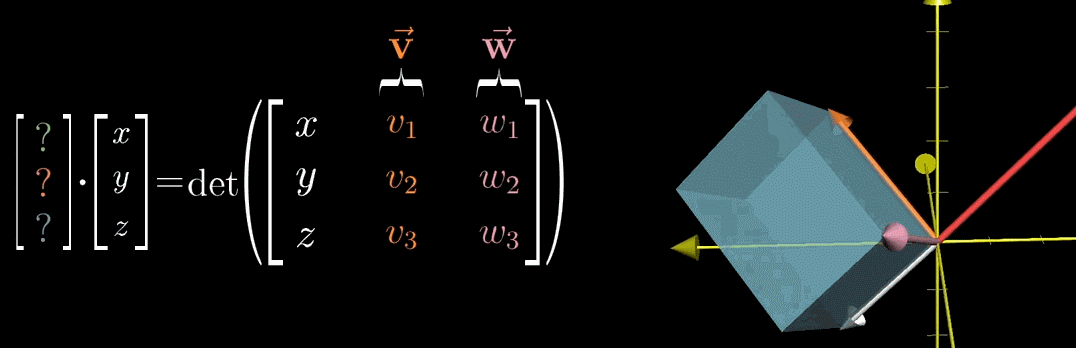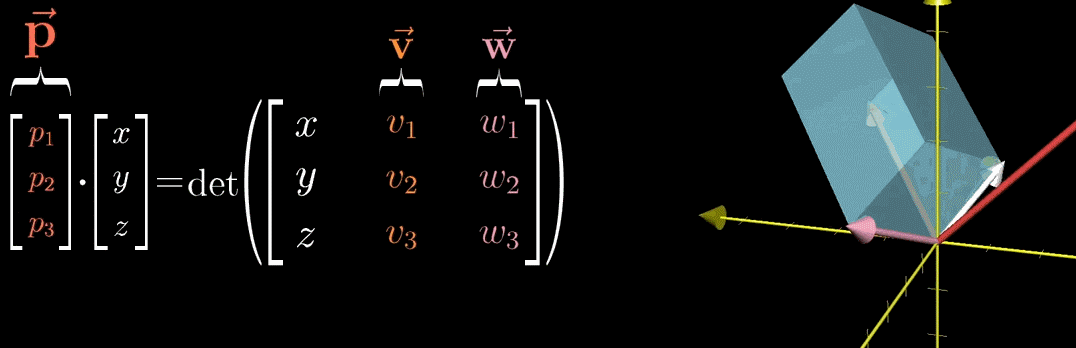
“将
1
×
3
1 \times 3
1×3 的变换矩阵转置,写成点积形式” 的逻辑 —— 通过对偶性,将 “线性变换作用于
u
⃗
\vec{u}
u” 转化为 “
u
⃗
\vec{u}
u 与
p
⃗
\vec{p}
p 的点积”,此时问题进一步转化为:寻找向量
p
⃗
\vec{p}
p,使得上述等式成立。
9.4.3 确定 p ⃗ \vec{p} p 的方向与长度
(1) p ⃗ \vec{p} p 的方向:与 v ⃗ \vec{v} v、 w ⃗ \vec{w} w 张成的平面垂直
根据点积的几何意义, p ⃗ ⋅ u ⃗ \vec{p} \cdot \vec{u} p⋅u 表示 “将 u ⃗ \vec{u} u 投影到 p ⃗ \vec{p} p 上,投影长度与 p ⃗ \vec{p} p 的长度相乘”;而平行六面体的体积公式为 “底面积 × 高”,其中 “高” 是 u ⃗ \vec{u} u 在 “与底面积垂直方向” 上的投影长度(底面积为 v ⃗ \vec{v} v 与 w ⃗ \vec{w} w 张成的平行四边形面积)。

为使 “点积结果” 与 “体积” 相等, p ⃗ \vec{p} p 的方向必须与 v ⃗ \vec{v} v、 w ⃗ \vec{w} w 张成的平面垂直 —— 只有这样, u ⃗ \vec{u} u 在 p ⃗ \vec{p} p 上的投影长度才等于平行六面体的高,满足 “体积 = 底面积 × 高” 的逻辑。
(2) p ⃗ \vec{p} p 的长度:等于 v ⃗ \vec{v} v、 w ⃗ \vec{w} w 张成的平行四边形面积
结合点积公式与体积公式:
-
点积: p ⃗ ⋅ u ⃗ = ∣ p ⃗ ∣ × ∣ u ⃗ 投影 ∣ \vec{p} \cdot \vec{u} = |\vec{p}| \times |\vec{u}_{\text{投影}}| p⋅u=∣p∣×∣u投影∣( ∣ u ⃗ 投影 ∣ |\vec{u}_{\text{投影}}| ∣u投影∣ 为 u ⃗ \vec{u} u 在 p ⃗ \vec{p} p 上的投影长度);
-
体积: V = S × ∣ u ⃗ 投影 ∣ V = S \times |\vec{u}_{\text{投影}}| V=S×∣u投影∣( S S S 为 v ⃗ \vec{v} v 与 w ⃗ \vec{w} w 张成的平行四边形面积)。
由于 p ⃗ ⋅ u ⃗ = V \vec{p} \cdot \vec{u} = V p⋅u=V,代入后可得 ∣ p ⃗ ∣ = S |\vec{p}| = S ∣p∣=S,即 p ⃗ \vec{p} p 的长度等于 v ⃗ \vec{v} v 与 w ⃗ \vec{w} w 张成的平行四边形面积。
9.4.4 对偶性的价值
通过上述推导,再次验证了对偶性的意义 —— 它建立了 “线性变换” 与 “向量” 之间自然且出乎意料的对应关系。基于几何直观理解叉积公式的由来,而非单纯记忆,是加深概念记忆、实现深度理解的有效途径。
9.5 总结
通过以下步骤可回顾叉积的核心逻辑,检验对概念的掌握程度:
-
基于 v ⃗ \vec{v} v 和 w ⃗ \vec{w} w,定义一个从三维空间到数轴的线性变换 f ( u ⃗ ) = det ( u ⃗ v ⃗ w ⃗ ) f(\vec{u}) = \det\begin{pmatrix} \vec{u} & \vec{v} & \vec{w} \end{pmatrix} f(u)=det(uvw);
-
利用对偶性,将线性变换 f ( u ⃗ ) f(\vec{u}) f(u) 转化为 “ u ⃗ \vec{u} u 与某向量 p ⃗ \vec{p} p 的点积”,即 f ( u ⃗ ) = p ⃗ ⋅ u ⃗ f(\vec{u}) = \vec{p} \cdot \vec{u} f(u)=p⋅u;
-
为满足 “点积结果 = 平行六面体体积”,推导得出: p ⃗ \vec{p} p 的方向与 v ⃗ \vec{v} v、 w ⃗ \vec{w} w 张成的平面垂直,长度等于该平面内平行四边形的面积;
-
将 ı ^ \hat{\imath} ^、 ȷ ^ \hat{\jmath} ^、 k ^ \hat{k} k^ 代入行列式第一列并展开,即可得到叉积的计算公式,而该行列式的结果向量正是对偶向量 p ⃗ \vec{p} p,即 v ⃗ × w ⃗ = p ⃗ \vec{v} \times \vec{w} = \vec{p} v×w=p。
在几何直观上,这个对偶向量一定与 v ⃗ \vec{v} v 和 w ⃗ \vec{w} w 垂直,并且其长度与这两个向量张成的平行四边形的面积相同。
10 基变换与坐标转换
Mathematics is the art of givinh the same name to different things -Henri Poincare
数学是一门赋予不同事物相同名称的艺术 ——昂利·庞加莱
10.1 基的定义与坐标表示
设
{
b
1
⃗
,
b
2
⃗
,
⋯
,
b
n
⃗
}
\{\vec {b_1}, \vec {b_2}, \cdots, \vec {b_n}\}
{b1,b2,⋯,bn} 是
n
n
n 维空间的一组基,任意向量
x
⃗
\vec {x}
x 可唯一表示为:
x
⃗
=
c
1
b
1
⃗
+
c
2
b
2
⃗
+
⋯
+
c
n
b
n
⃗
\vec {x} = c_1\vec {b_1} + c_2\vec {b_2} + \cdots + c_n\vec {b_n}
x=c1b1+c2b2+⋯+cnbn
其中
[
c
1
c
2
⋯
c
n
]
\begin {bmatrix} c_1 \\ c_2 \\ \cdots \\ c_n \end {bmatrix}
c1c2⋯cn
称为
x
⃗
\vec {x}
x 在基
{
b
1
⃗
,
⋯
,
b
n
⃗
}
\{\vec {b_1}, \cdots, \vec {b_n}\}
{b1,⋯,bn} 下的坐标。
10.1.2 标准基与非标准基的转换
设标准基为 { ı ^ , ȷ ^ } \{\hat {\imath}, \hat {\jmath}\} {^,^}(二维),非标准基为 { b 1 ⃗ , b 2 ⃗ } \{\vec {b_1}, \vec {b_2}\} {b1,b2},其中 b 1 ⃗ = [ 2 1 ] \vec {b_1} = \begin {bmatrix} 2 \\ 1 \end {bmatrix} b1=[21], b 2 ⃗ = [ − 1 1 ] \vec {b_2} = \begin {bmatrix} -1 \\ 1 \end {bmatrix} b2=[−11](用标准基表示)。
- 基变换矩阵:将非标准基向量作为列构成矩阵 T = [ 2 − 1 1 1 ] T = \begin {bmatrix} 2 & -1 \\ 1 & 1 \end {bmatrix} T=[21−11],称为 “从非标准基到标准基的转换矩阵”;
- 坐标转换:若 x ⃗ \vec {x} x 在非标准基下的坐标为 [ c 1 c 2 ] \begin {bmatrix} c_1 \\ c_2 \end {bmatrix} [c1c2],则其在标准基下的坐标为 [ x 1 x 2 ] = T [ c 1 c 2 ] \begin {bmatrix} x_1 \\ x_2 \end {bmatrix} = T\begin {bmatrix} c_1 \\ c_2 \end {bmatrix} [x1x2]=T[c1c2];
- 逆转换:若已知 x ⃗ \vec {x} x 在标准基下的坐标,其在非标准基下的坐标为 [ c 1 c 2 ] = T − 1 [ x 1 x 2 ] \begin {bmatrix} c_1 \\ c_2 \end {bmatrix} = T^{-1}\begin {bmatrix} x_1 \\ x_2 \end {bmatrix} [c1c2]=T−1[x1x2],其中 T − 1 T^{-1} T−1 是 T T T 的逆矩阵。
10.2 线性变换在不同基下的矩阵
设线性变换
L
L
L 在标准基下的矩阵为
M
M
M,在非标准基
{
b
1
⃗
,
b
2
⃗
}
\{\vec {b_1}, \vec {b_2}\}
{b1,b2} 下的矩阵为
M
′
M'
M′,则
M
′
M'
M′ 与
M
M
M 的关系为:
M
′
=
T
−
1
M
T
M' = T^{-1} MT
M′=T−1MT
其中
T
T
T 是从非标准基到标准基的转换矩阵。
10.2.2 几何意义
- T T T:将非标准基下的坐标转换为标准基下的坐标;
- M M M:在标准基下应用线性变换;
- T − 1 T^{-1} T−1:将标准基下的变换结果转换回非标准基下的坐标;
- 整体效果: M ′ M' M′ 描述了同一线性变换在非标准基下的数字表达。
示例:设
L
L
L 是 “左旋转
9
0
∘
90^\circ
90∘” 的变换,标准基下的矩阵
M
=
[
0
−
1
1
0
]
M = \begin {bmatrix} 0 & -1 \\ 1 & 0 \end {bmatrix}
M=[01−10],非标准基转换矩阵
T
=
[
2
−
1
1
1
]
T = \begin {bmatrix} 2 & -1 \\ 1 & 1 \end {bmatrix}
T=[21−11],则非标准基下的变换矩阵为:
M
′
=
T
−
1
M
T
=
1
3
[
1
1
−
1
2
]
×
[
0
−
1
1
0
]
×
[
2
−
1
1
1
]
=
[
1
3
−
1
3
2
3
−
1
]
M' = T^{-1} MT = \frac {1}{3}\begin {bmatrix} 1 & 1 \\ -1 & 2 \end {bmatrix} \times \begin {bmatrix} 0 & -1 \\ 1 & 0 \end {bmatrix} \times \begin {bmatrix} 2 & -1 \\ 1 & 1 \end {bmatrix} = \begin {bmatrix} \frac {1}{3} & -\frac {1}{3} \\ \frac {2}{3} & -1 \end {bmatrix}
M′=T−1MT=31[1−112]×[01−10]×[21−11]=[3132−31−1]
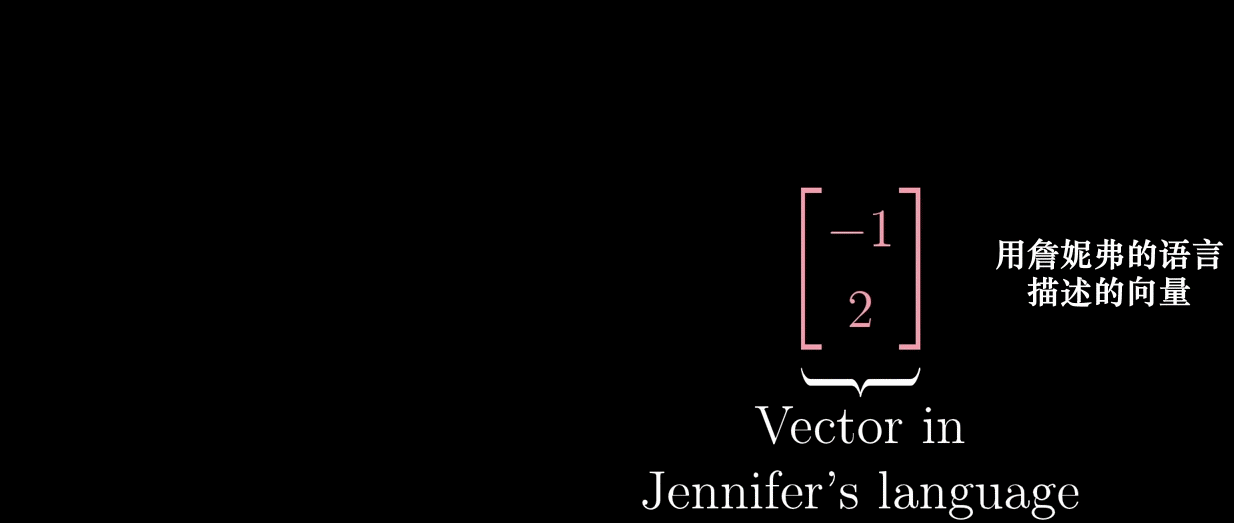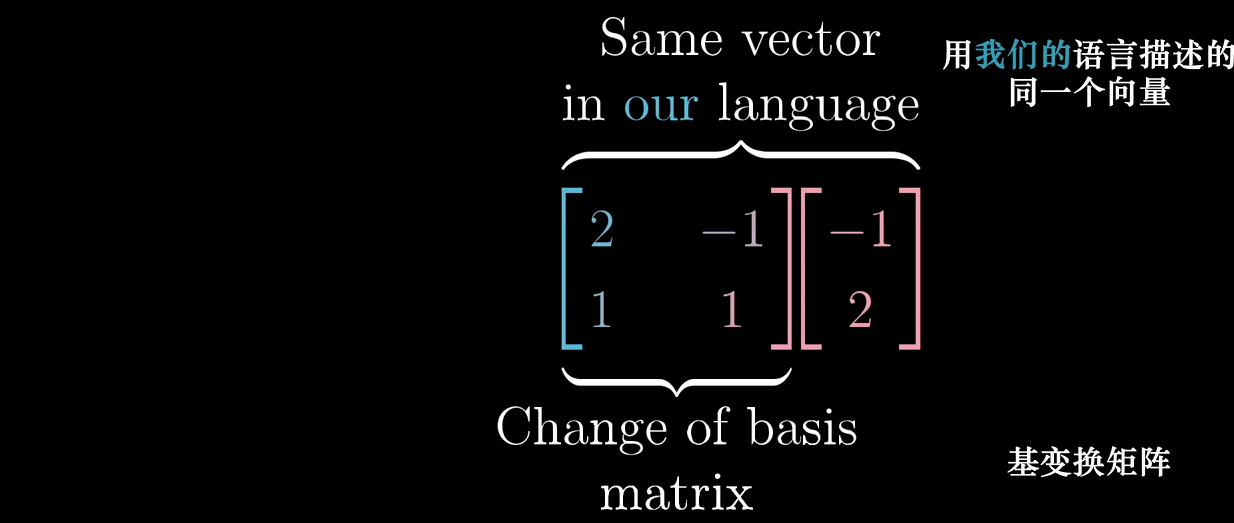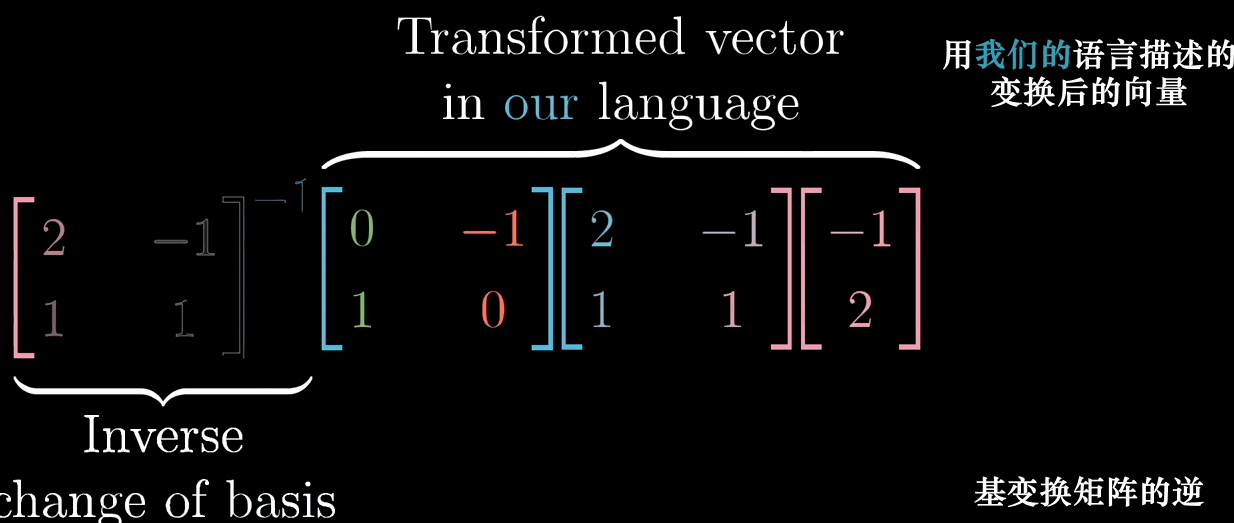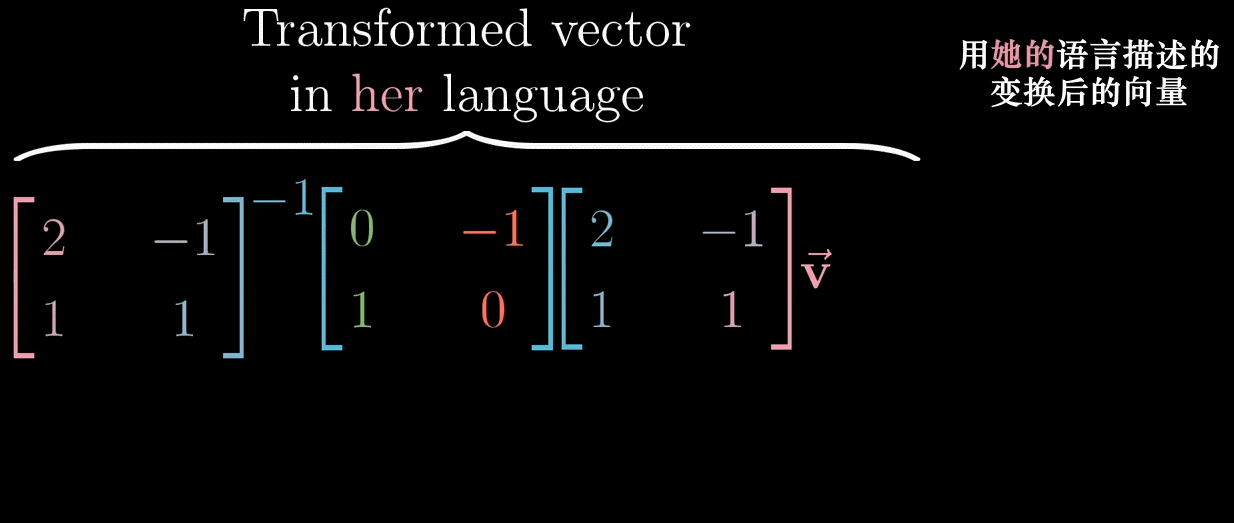
11 特征向量与特征值
本节将系统梳理特征向量与特征值的定义、意义、计算方法及特殊情况,同时探讨特征基的应用,建立其与线性变换、行列式等前置知识的关联,深化对线性代数变换本质的理解。
11.1 特征向量与特征值的定义
设对 ı ^ \hat{\imath} ^ 和 ȷ ^ \hat{\jmath} ^ 张成的空间进行线性变换,基变换为 ı ^ ′ = [ 3 0 ] \hat{\imath}' = \begin{bmatrix} 3 \\ 0 \end{bmatrix} ^′=[30]、 ȷ ^ ′ = [ 1 2 ] \hat{\jmath}' = \begin{bmatrix} 1 \\ 2 \end{bmatrix} ^′=[12]。变换中,大部分向量会脱离自身张成空间(原点到向量终点的直线),但部分向量仍留在该空间内,仅被拉伸或压缩。

如图所示, x x x 轴上所有向量被伸长为原来的 3 倍,向量 ( − 1 , 1 ) (-1, 1) (−1,1) 被伸长为原来的 2 倍,基于此可给出如下定义:
- 变换中留在自身张成空间内的向量,称为特征向量(如 x x x 轴上的向量、 ( − 1 , 1 ) (-1, 1) (−1,1));
- 特征向量被拉伸或压缩的比例因子,称为特征值(如 3、2);
- 特征值的正负号,用于表示变换是否使向量发生方向翻转。
11.2 特征向量与特征值的意义
特征向量与特征值是理解线性变换作用的关键工具。以三维空间为例,若能找到旋转轴对应的向量,其特征值必为 1,该向量在旋转变换中保持方向不变,通过这类特征信息可更清晰地描述线性变换的本质。
11.3 特征向量与特征值的计算
根据定义,特征向量与特征值满足数学关系 A v ⃗ = λ v ⃗ A \vec{v} = \lambda \vec{v} Av=λv,其中 A A A 为变换矩阵, v ⃗ \vec{v} v 为特征向量, λ \lambda λ 为特征值。为便于计算,将等式变形为矩阵乘法形式:
- 由于 λ v ⃗ \lambda \vec{v} λv 等价于对角矩阵 λ I \lambda I λI 与 v ⃗ \vec{v} v 的乘积( I I I 为单位矩阵),因此 A v ⃗ = ( λ I ) v ⃗ A \vec{v} = (\lambda I) \vec{v} Av=(λI)v;
- 移项可得 ( A − λ I ) v ⃗ = 0 (A - \lambda I) \vec{v} = 0 (A−λI)v=0,该式表示矩阵 A − λ I A - \lambda I A−λI 对 v ⃗ \vec{v} v 的变换会将其压缩到更低维度;
- 空间压缩对应矩阵行列式为 0,即 det ( A − λ I ) = 0 \det(A - \lambda I) = 0 det(A−λI)=0,求解该方程可得到特征值 λ \lambda λ,再代入 ( A − λ I ) v ⃗ = 0 (A - \lambda I) \vec{v} = 0 (A−λI)v=0 可求得特征向量 v ⃗ \vec{v} v。
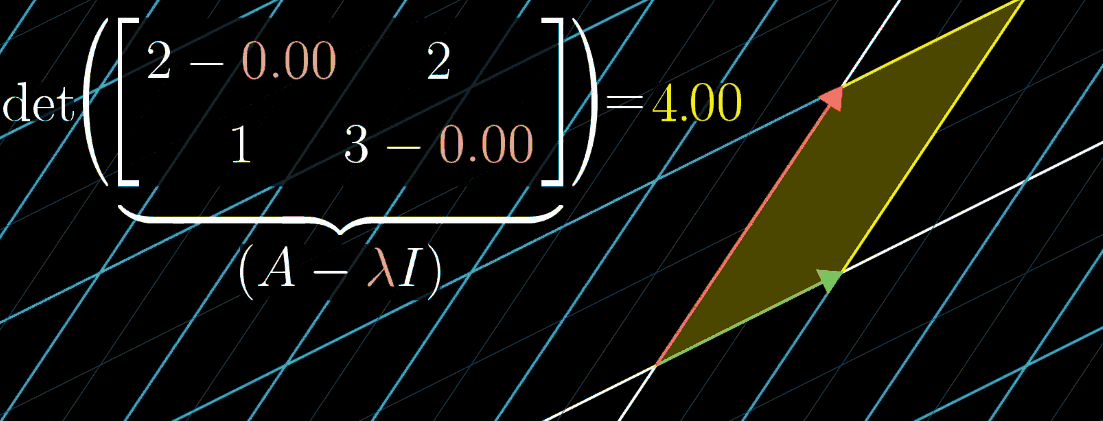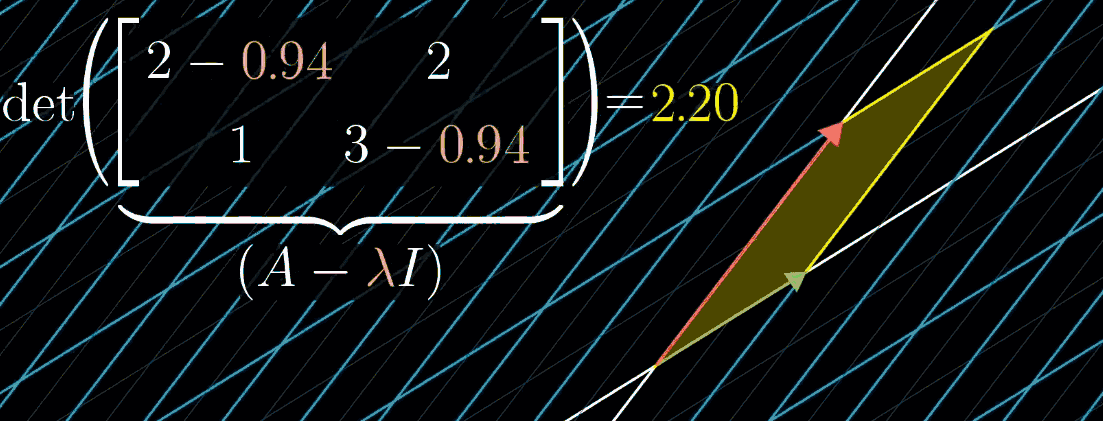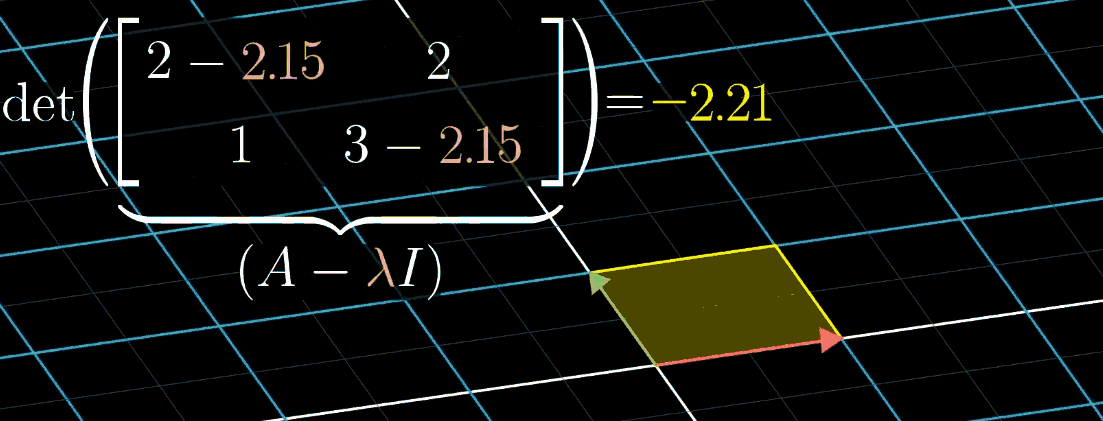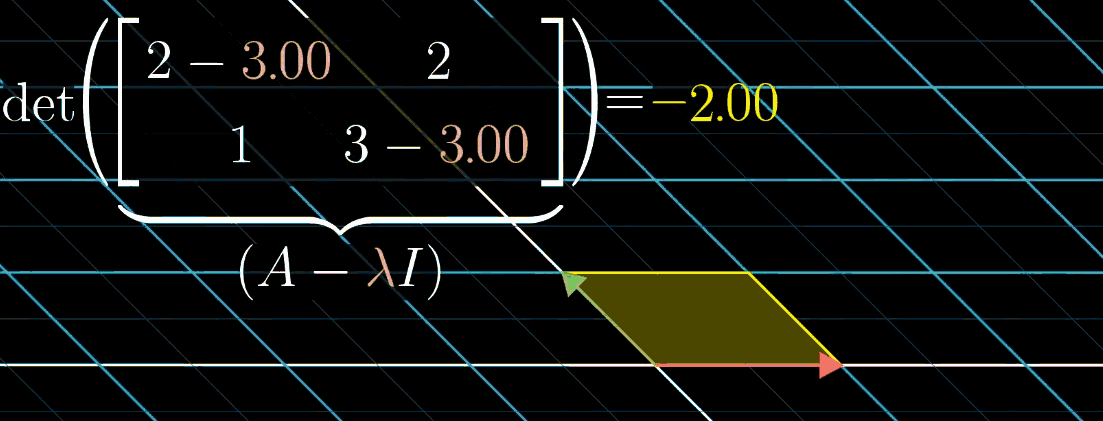
如图所示,随 λ \lambda λ 变化可可视化这一计算过程。例如矩阵 A = [ 2 2 1 3 ] A = \begin{bmatrix} 2 & 2 \\ 1 & 3 \end{bmatrix} A=[2123],其特征值之一为 1。
11.4 特征向量的特殊情况
11.4.1 旋转变换
对平面旋转变换,求解特征值会得到复数解(如 ± i \pm i ±i),不存在实特征向量。特征值为复数的情况,通常对应变换中的旋转操作。
11.4.2 剪切变换
剪切变换中, x x x 轴保持不变,仅存在一个特征值 λ = 1 \lambda = 1 λ=1(满足 ( λ − 1 ) 2 = 0 (\lambda - 1)^2 = 0 (λ−1)2=0),且特征向量数量不足,无法张成整个空间。
11.4.3 伸缩变换
伸缩变换中,仅有一个特征值,但空间内所有向量均为特征向量,变换仅对所有向量进行统一比例的拉伸或压缩。
11.5 特征基
- 定义:由特征向量构成的基向量集合,称为特征基。对角矩阵的基向量均为特征向量,因其列向量(对应基向量)仅在自身维度上有非零值,符合特征向量“方向不变”的属性。
- 优势:对角矩阵的多次乘法计算简便,例如 A n A^n An( A A A 为对角矩阵)仅需对对角线元素取 n n n 次幂。
- 应用:若矩阵可对角化,可通过基变换将其转化为对角矩阵计算:以特征向量为基构建变换矩阵 P P P,则 P − 1 A P P^{-1}AP P−1AP 为对角矩阵(对角元素为特征值),计算后再通过 P P P 转换回原空间。
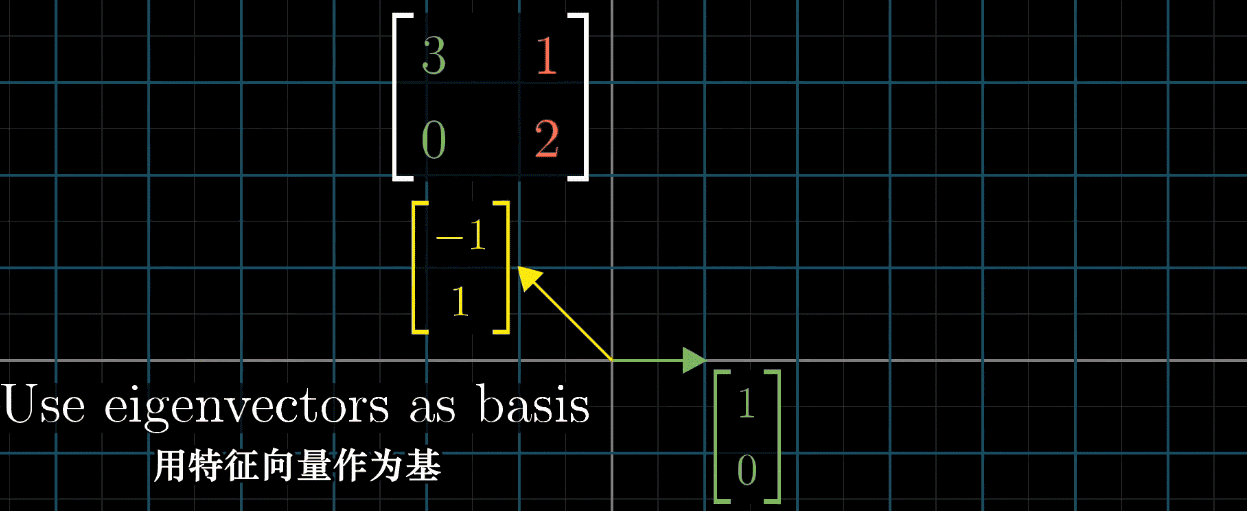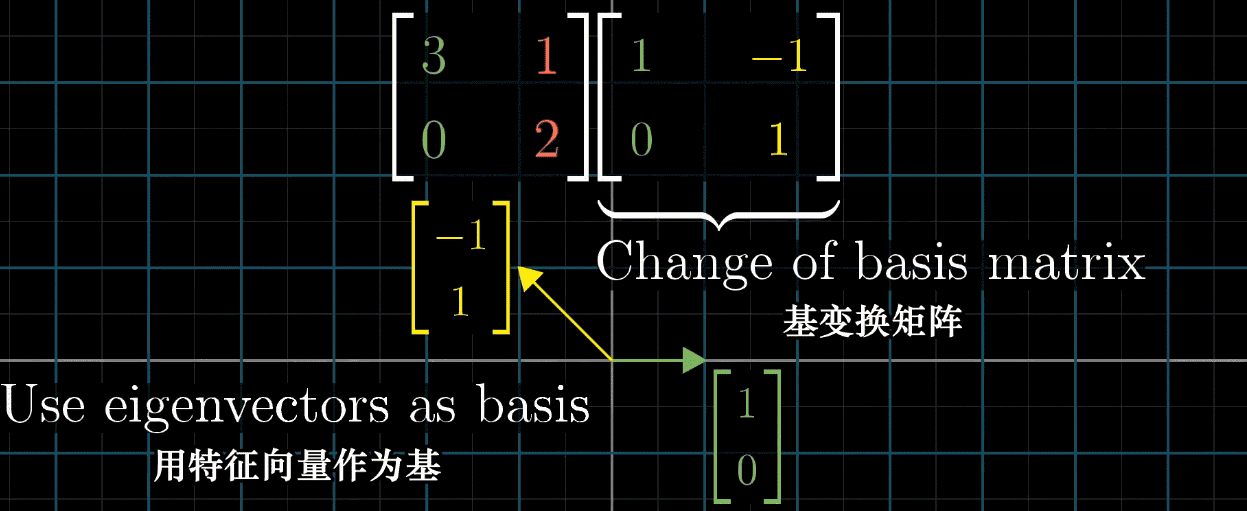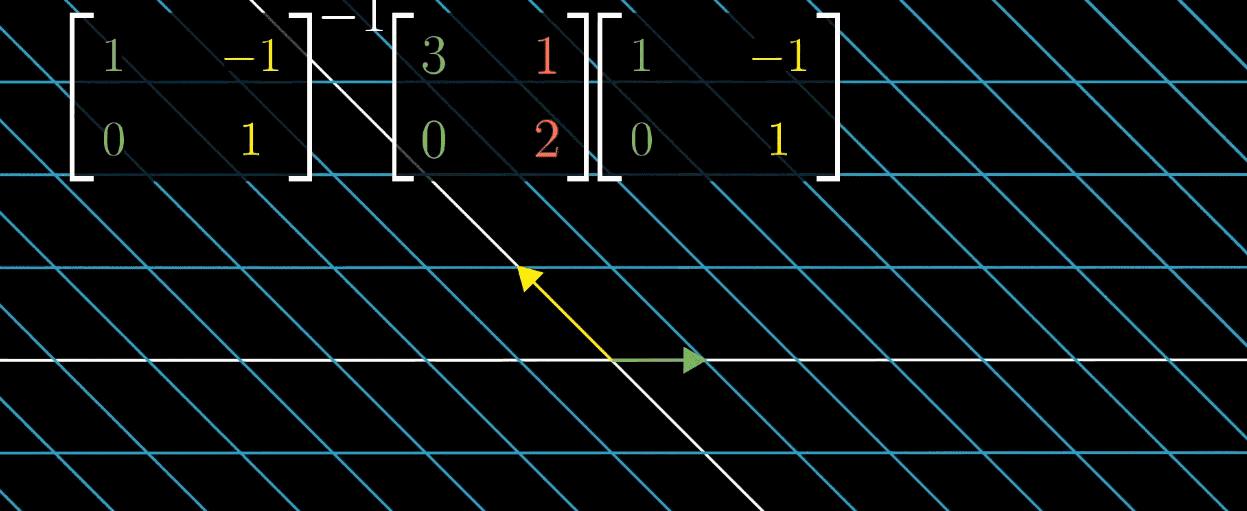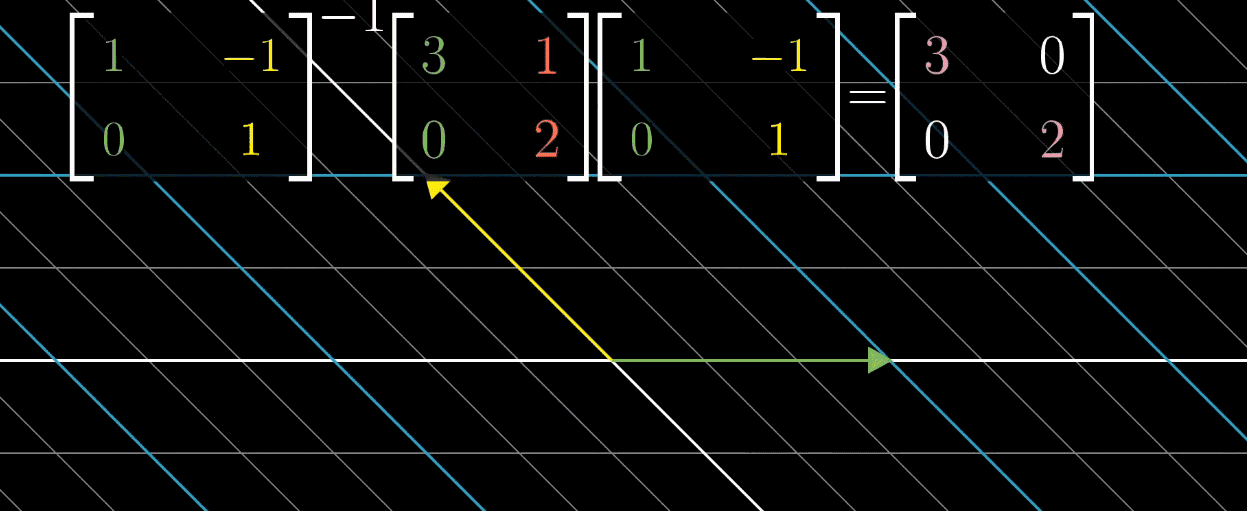
需注意,并非所有矩阵都能对角化,如剪切变换因特征向量数量不足,无法构建特征基。
12 抽象向量空间
线性代数的关键概念(如行列式、特征向量)不受坐标系限制,是空间的固有属性。
本节将线性代数的应用范围从“箭头向量”扩展到更广泛的抽象对象,构建抽象向量空间的理论框架。
12.1 函数与向量的等价性
函数可视为一种特殊的“向量”,因其满足向量的关键运算性质:
- 可加性: ( f + g ) ( x ) = f ( x ) + g ( x ) (f + g)(x) = f(x) + g(x) (f+g)(x)=f(x)+g(x),即两个函数在任意点的函数值之和,对应向量加法;
- 数乘性: ( k f ) ( x ) = k f ( x ) (kf)(x) = kf(x) (kf)(x)=kf(x)( k k k 为标量),即标量与函数值的乘积,对应向量数乘。
基于此,线性代数中矩阵、线性变换等概念可迁移至函数领域。例如,微积分中的导数是典型的函数线性变换,通常称为“线性算子”,其本质与向量空间中的线性变换一致。
以多项式函数为例,可通过矩阵描述求导变换。选取幂函数 { 1 , x , x 2 , x 3 , … } \{1, x, x^2, x^3, \dots\} {1,x,x2,x3,…} 作为基函数(对应向量空间的基向量),则求导操作可表示为矩阵形式,进一步验证“矩阵是变换的数字表达”这一关键观点。
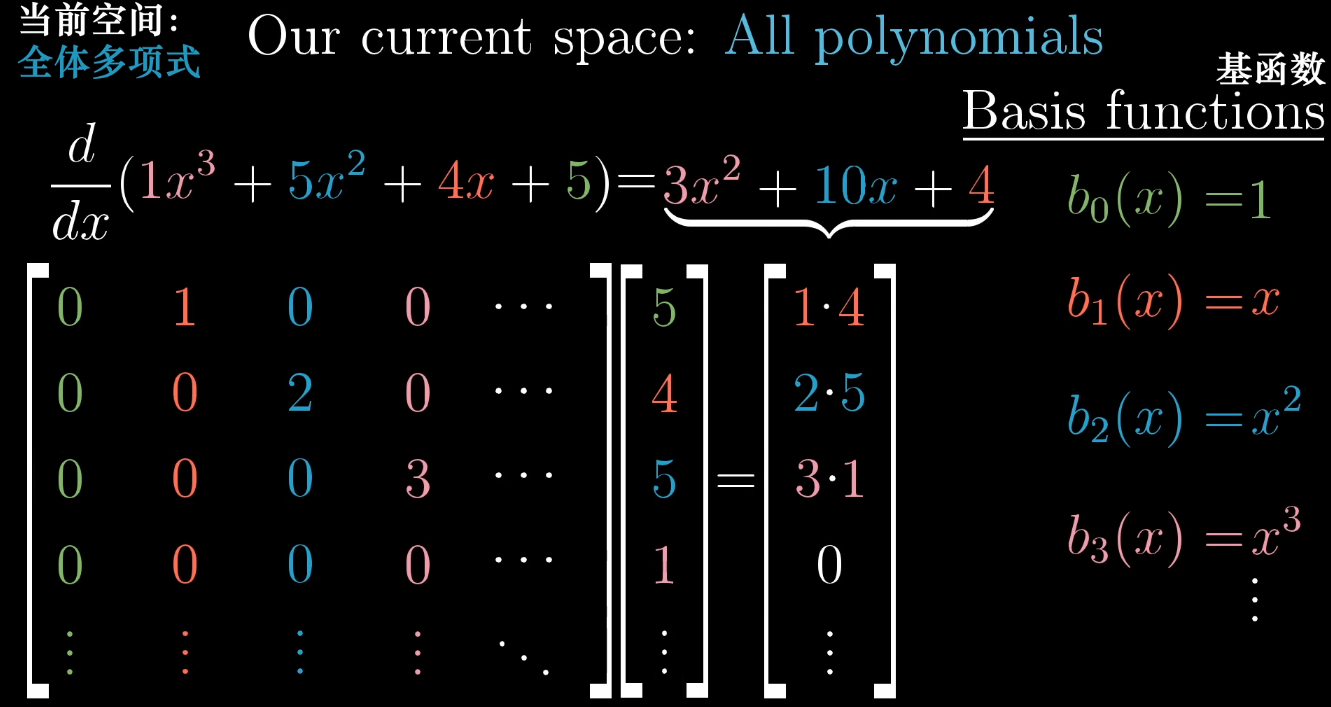
12.2 向量空间的定义与公理
- 定义:满足向量加法和数乘运算规则的集合,称为向量空间,集合中的元素称为“向量”(如箭头、数组、函数等)。
- 公理:向量加法与数乘需满足以下 8 条公理,以保证运算的合理性:

- 向量加法结合律: r ⃗ + ( v ⃗ + w ⃗ ) = ( r ⃗ + v ⃗ ) + w ⃗ \vec{r} + (\vec{v} + \vec{w}) = (\vec{r} + \vec{v}) + \vec{w} r+(v+w)=(r+v)+w;
- 向量加法交换律: v ⃗ + w ⃗ = w ⃗ + v ⃗ \vec{v} + \vec{w} = \vec{w} + \vec{v} v+w=w+v;
- 加法单位元存在:存在零向量 0 ⃗ \vec{0} 0,使得 0 ⃗ + v ⃗ = v ⃗ \vec{0} + \vec{v} = \vec{v} 0+v=v 对所有 v ⃗ \vec{v} v 成立;
- 加法逆元存在:对任意向量 v ⃗ \vec{v} v,存在 − v ⃗ \vec{-v} −v,使得 v ⃗ + ( − v ⃗ ) = 0 ⃗ \vec{v} + (-\vec{v}) = \vec{0} v+(−v)=0;
- 标量乘法与域乘法相容: a ( b v ⃗ ) = ( a b ) v ⃗ a(b\vec{v}) = (ab)\vec{v} a(bv)=(ab)v( a , b a, b a,b 为标量);
- 标量乘法单位元存在: 1 ⋅ v ⃗ = v ⃗ 1 \cdot \vec{v} = \vec{v} 1⋅v=v;
- 标量乘法对向量加法分配律: a ( v ⃗ + w ⃗ ) = a v ⃗ + a w ⃗ a(\vec{v} + \vec{w}) = a\vec{v} + a\vec{w} a(v+w)=av+aw;
- 标量乘法对域加法分配律: ( a + b ) v ⃗ = a v ⃗ + b v ⃗ (a + b)\vec{v} = a\vec{v} + b\vec{v} (a+b)v=av+bv。
这些公理是连接理论与应用的桥梁,确保线性代数结论可推广到各类抽象向量空间。
12.3 函数空间示例:多项式空间
以“所有多项式构成的集合”为例,验证其满足抽象向量空间的定义:
- 向量加法:设多项式 f ( x ) = a n x n + ⋯ + a 1 x + a 0 f(x) = a_nx^n + \dots + a_1x + a_0 f(x)=anxn+⋯+a1x+a0、 g ( x ) = b n x n + ⋯ + b 1 x + b 0 g(x) = b_nx^n + \dots + b_1x + b_0 g(x)=bnxn+⋯+b1x+b0,则 f ( x ) + g ( x ) = ( a n + b n ) x n + ⋯ + ( a 1 + b 1 ) x + ( a 0 + b 0 ) f(x) + g(x) = (a_n + b_n)x^n + \dots + (a_1 + b_1)x + (a_0 + b_0) f(x)+g(x)=(an+bn)xn+⋯+(a1+b1)x+(a0+b0),符合可加性;
- 向量数乘:对标量 c c c, c ⋅ f ( x ) = c a n x n + ⋯ + c a 1 x + c a 0 c \cdot f(x) = ca_nx^n + \dots + ca_1x + ca_0 c⋅f(x)=canxn+⋯+ca1x+ca0,符合数乘性;
- 基与维度: n n n 次多项式空间的基为 { 1 , x , x 2 , … , x n } \{1, x, x^2, \dots, x^n\} {1,x,x2,…,xn},维度为 n + 1 n + 1 n+1(基向量的个数)。
12.4 线性算子:抽象空间的线性变换
在抽象向量空间中,“线性变换”称为线性算子,需满足与线性变换相同的条件:对任意向量 u ⃗ , v ⃗ \vec{u}, \vec{v} u,v 和标量 k k k,有 T ( u ⃗ + v ⃗ ) = T ( u ⃗ ) + T ( v ⃗ ) T(\vec{u} + \vec{v}) = T(\vec{u}) + T(\vec{v}) T(u+v)=T(u)+T(v) 且 T ( k u ⃗ ) = k T ( u ⃗ ) T(k\vec{u}) = kT(\vec{u}) T(ku)=kT(u)。
12.4.1 导数算子示例
设导数算子 D : D ( f ( x ) ) = f ′ ( x ) D: D(f(x)) = f'(x) D:D(f(x))=f′(x)(作用于多项式空间),验证其线性性:
- 可加性: D ( f ( x ) + g ( x ) ) = f ′ ( x ) + g ′ ( x ) = D ( f ( x ) ) + D ( g ( x ) ) D(f(x) + g(x)) = f'(x) + g'(x) = D(f(x)) + D(g(x)) D(f(x)+g(x))=f′(x)+g′(x)=D(f(x))+D(g(x));
- 数乘性: D ( k f ( x ) ) = k f ′ ( x ) = k D ( f ( x ) ) D(kf(x)) = kf'(x) = kD(f(x)) D(kf(x))=kf′(x)=kD(f(x))。
以
{
1
,
x
,
x
2
}
\{1, x, x^2\}
{1,x,x2} 为基,多项式
f
(
x
)
=
a
+
b
x
+
c
x
2
f(x) = a + bx + cx^2
f(x)=a+bx+cx2 的坐标为
[
a
b
c
]
\begin{bmatrix} a \\ b \\ c \end{bmatrix}
abc
,其导数
f
′
(
x
)
=
b
+
2
c
x
f'(x) = b + 2cx
f′(x)=b+2cx 的坐标为
[
b
2
c
0
]
\begin{bmatrix} b \\ 2c \\ 0 \end{bmatrix}
b2c0
,因此导数算子对应的矩阵为:
D
=
[
0
1
0
0
0
2
0
0
0
]
D = \begin{bmatrix} 0 & 1 & 0 \\ 0 & 0 & 2 \\ 0 & 0 & 0 \end{bmatrix}
D=
000100020
12.5 概念的统一与扩展
抽象向量空间中,线性代数关键概念可对应扩展,不同领域术语本质一致,具体如下表所示:
| 线性代数术语 | 抽象向量空间术语 | 函数空间示例 |
|---|---|---|
| 线性变换 | 线性算子 | 导数 D ( f ( x ) ) = f ′ ( x ) D(f(x)) = f'(x) D(f(x))=f′(x) |
| 点积 | 内积 | 积分内积 ⟨ f , g ⟩ = ∫ a b f ( x ) g ( x ) d x \langle f, g \rangle = \int_a^b f(x)g(x)dx ⟨f,g⟩=∫abf(x)g(x)dx |
| 特征向量 | 特征函数 | 微分方程 D ( f ( x ) ) = λ f ( x ) D(f(x)) = \lambda f(x) D(f(x))=λf(x) 的解 f ( x ) = e λ x f(x) = e^{\lambda x} f(x)=eλx |
只要对象满足加法与数乘规则,线性代数的所有结论均可适用,体现了数学规律的普适性。
12.6 总结
- 向量的本质:向量并非局限于箭头或数组,而是满足加法与数乘公理的抽象对象,类似“3”是对“三个事物”的抽象,向量空间是对“具有线性运算属性的集合”的抽象;
- 抽象性与普适性:抽象性是实现普适性的代价(abstractness is the price of generality)。通过公理定义向量空间,可将线性代数应用于函数、多项式等各类领域;
- 线性代数的关键框架:
- 向量:满足线性运算的抽象对象;
- 矩阵:线性变换的数字表达,列向量对应基向量的变换结果;
- 行列式:空间体积的缩放比例,决定矩阵可逆性;
- 特征向量/值:变换中方向不变的向量与缩放比例,揭示变换本质;
- 抽象向量空间:扩展线性代数的应用范围,实现概念统一。
学习线性代数的关键在于建立“几何直观”而非记忆公式,通过理解概念间的关联,可在机器学习、机器人控制等工程领域灵活应用,突破单纯的计算层面。
学习的过程只能来源于解决问题,来源于带有思考的不断重复,但如果你具备了正确的直观,你会再以后的学习中更加高效。
via:
-
【直观详解】线性代数的本质 | Go Further | Stay Hungry, Stay Foolish
https://charlesliuyx.github.io/2017/10/06/【直观详解】线性代数的本质/ -
Determinant - Note201.pdf - 21 February, 2019
https://math.ntnu.edu.tw/~li/Linear/Note201.pdf
 线性代数的本质与几何直观
线性代数的本质与几何直观





















 8243
8243

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








