傅里叶变换 | 时移、频移及应用

原创已于 2025-10-07 17:30:28 修改 · 1.3k 阅读

24 ·

CC 4.0 BY-SA版权

文章标签：

#傅里叶变换

于 2025-10-07 14:55:53 首次发布

signals and systems 专栏收录该内容

15 篇文章

订阅专栏

注：本文为 “傅里叶变换” 相关合集。
略作重排，未整理去重。
图片清晰度限于引文原状。
如有内容异常，请看原文。

信号处理 – 傅里叶变换的性质及常用信号的傅里叶变换

知知知_了于 2020-10-23 12:25:36 发布

一、前言

傅里叶变换的定义式

在这里插入图片描述

函数 $f (t)$ 的傅里叶变换存在的充分条件是在无限区间内 $f (t)$ 绝对可积，但它并非必要条件。

在这里插入图片描述

当引入广义函数的概念后，许多不满足绝对可积条件的函数也能进行傅里叶变换，这给信号与系统分析带来很大方便。

二、傅里叶变换的性质

在这里插入图片描述

三、奇异函数的傅里叶变换

1、冲激函数的频谱

方法一：根据傅里叶变换的定义式，并且考虑到冲激函数的取样性质，得

在这里插入图片描述

其频谱密度在 $-\infty<\omega<\infty$ 区间处处相等，常称为 “均匀谱” 或 “白色频谱”。

方法二：应用广义极限的概念，单位冲激函数 $\delta(t)$ 是幅度为 $\frac{1}{\tau}$ ，脉宽为 $\tau$ 的矩形脉冲当 $\tau\rightarrow0$ 的广义极限，因而可以写为

在这里插入图片描述

门函数的傅里叶变换

在这里插入图片描述

因而

在这里插入图片描述

所以

在这里插入图片描述

2、冲激函数导数的频谱

冲激函数导数定义式为

在这里插入图片描述

其中 $\varphi(t)$ 为检验函数， $\varphi(t)$ 是急降的。

按广义函数理论，由于选取了性能良好的检验函数空间 $\Phi$ ，广义函数的各阶导数都存在并且仍属于缓增广义函数空间 $\Phi^{\prime}$ 。

根据定义，冲激函数的一阶导数 $\delta^{\prime}(t)$ 的频谱函数为：

在这里插入图片描述

即 $\delta^{\prime}(t)$ 的频谱函数为：

在这里插入图片描述

3、单位直流信号的频谱

幅度等于 $1$ 的直流信号可表示为 $-\infty < t < \infty$

显然，该信号不满足绝对可积条件，但其傅里叶变换却存在。

根据傅里叶变换的性质（对称性），可得

在这里插入图片描述

4、符号函数的频谱

符号函数记作 $s g n (t)$ ，它的定义为：

在这里插入图片描述

显然，该函数也不满足绝对可积条件。

函数 $s g n (t)$ 可看作是：

在这里插入图片描述

当 $\alpha$ 趋于 $0$ 时的极限，因此其频谱函数也是 $f_{1}(t)$ 的频谱函数 $F_{1}(j\omega)$ 当 $\alpha$ 趋于 $0$ 时的极限。

在这里插入图片描述

它是 $\omega$ 的奇函数，在 $\omega = 0$ 处 $F_{1}(0)=0$ ，因此当 $\alpha$ 趋近于零时，有：

在这里插入图片描述

于是得

在这里插入图片描述

5、阶跃函数的频谱

单位阶跃函数 $u (t)$ 也不满足绝对可积条件。它可看作是幅度为 $\frac{1}{2}$ 的直流信号与幅度为 $\frac{1}{2}$ 的符号函数之和，即：

对上式两边进行傅里叶变换，得

在这里插入图片描述

四、常用信号的傅里叶变换表

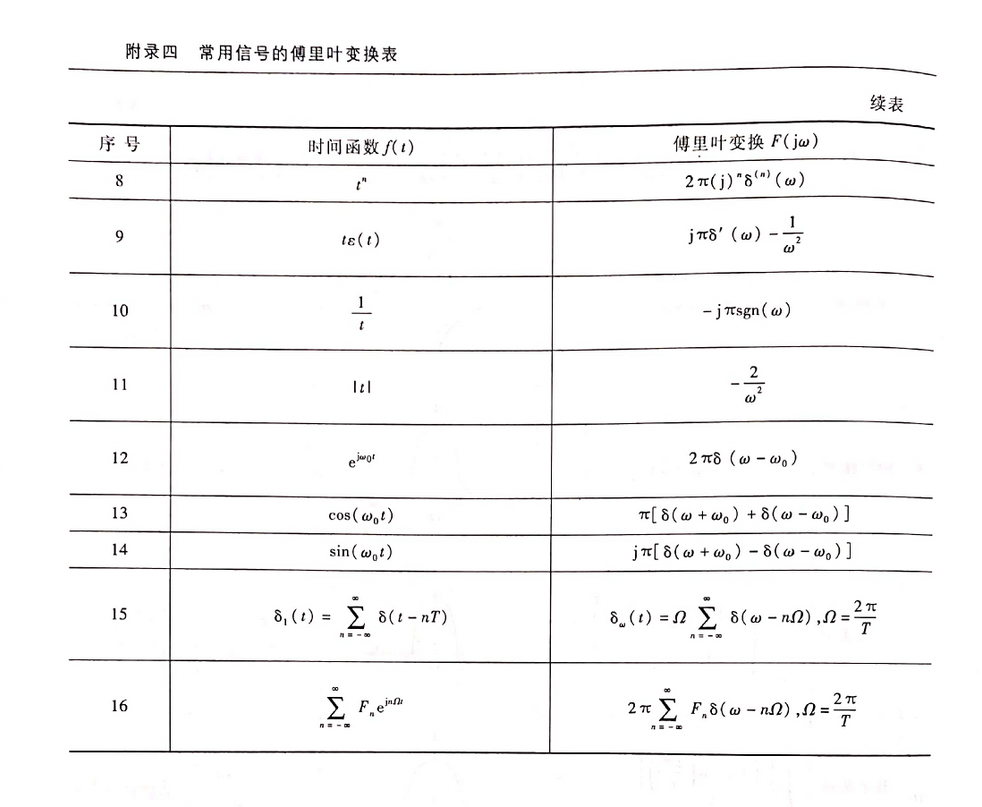
在这里插入图片描述

常用函数的傅里叶变换及其频谱

YprgDay于 2023-12-05 15:42:07 发布

本文围绕管致中的《信号与线性系统》上册，探讨了信号处理的基础理论，包括线性系统的数学模型、频域和时域分析方法，以及滤波器设计等内容。

表3-1 傅里叶变换表(几种常用函数及其频谱）

在这里插入图片描述

参考:《信号与线性系统（上册）》管致中

领悟《信号与系统》之傅里叶变换的性质与应用

太阳风暴已于 2023-08-16 13:28:49 修改

依据傅里叶变换对的概念，非周期连续时间信号可表述为指数函数的积分。利用该积分的性质，可建立时域与频域之间的关联，并推导得到一系列简化运算的公式。

一、傅里叶变换性质表

在这里插入图片描述

二、傅里叶性质详细说明

（一）傅里叶变换式

在这里插入图片描述

该变换式建立了信号时域与频域的映射关系，因此同一信号可通过时域与频域两种形式描述，且两种形式可相互转换。本节重点分析信号在时域中进行运算或变换时，在频域中产生的对应效应。

1. 线性性质

利用线性性质可将复合信号分解为多个简单信号分量，分别求解各分量的傅里叶变换后再进行合并，核心思想是通过“分解-求解-合并”的步骤简化复杂问题。该性质与线性时不变（Linear Time-Invariant, LTI）系统的线性齐次变换特性一致。

（1）定义

在这里插入图片描述

（2）例题

在这里插入图片描述

2. 尺度变换特性

尺度变换特性的核心规律为：

连续时间信号在时域展宽（ $0 < a < 1$ ）时，其频谱在频域压缩；
信号在时域压缩（ $a > 1$ ）时，其频谱在频域展宽；
若 $a < 0$ ，则信号时域波形反转，同时伴随压缩或展宽。

该特性揭示了时间与频率的反比关系，通常称为“时频展缩”。由周期 $T$ 与频率 $F$ 的关系 $F = 1/ T$ 可直接验证这一反比特性。

在信号处理系统设计中，尺度变换特性是关键考量因素。例如，若需提高系统传输效率，需对传输信号进行时域压缩，但压缩后的信号要求系统具备更宽的频带。

（1）定义

在这里插入图片描述

（2）证明

在这里插入图片描述

（3）例题

在这里插入图片描述

3. 时移特性

时移特性表明：当信号在时域发生移位（反映信号接入时间的变化）时，其幅度频谱保持不变，而相位频谱会叠加一个与角频率 $\omega$ 成线性关系的附加相移 $±ωt0 \pm \omega t_0$ （ $t_0$ 为时域移位量）。

（1）定义

在这里插入图片描述

（2）证明

在这里插入图片描述

（3）例题

在这里插入图片描述

4. 频移特性

频移特性是信号处理中应用最广泛的性质之一，其核心功能是实现“频谱搬移”。

（1）定义

在这里插入图片描述

（2）证明

在这里插入图片描述

（3）例题

在这里插入图片描述

（4）工程应用

频移特性在调幅、同步解调等电子系统中不可或缺，其核心原理是：在时域将信号 $f (t)$ （称为调制信号）与载波信号 $\cos(\omega_0 t)$ 或 $\sin(\omega_0 t)$ 相乘，得到高频已调信号 $y (t)$ ，即：
$\cdot \cos(\omega_0 t)$

频谱搬移的原理示意图如下：

在这里插入图片描述

下图给出了门函数及高频脉冲信号的时域波形与对应频谱：

在这里插入图片描述

由图可见：当用低频信号 $f (t)$ 对载频为 $\omega_0$ 的正弦信号进行幅度调制时，高频已调信号的频谱是将 $f (t)$ 的频谱 $F(j\omega)$ 按比例复制为两份，分别向 $\omega = \omega_0$ 和 $\omega = -\omega_0$ 方向搬移，且搬移过程中幅度频谱的形态保持不变。这一过程即为电子技术中的“调幅”。

5. 时域微分特性

时域微分特性的核心作用是：将时域的微分运算转换为频域的乘法运算，从而简化运算过程。

（1）定义

在这里插入图片描述

（2）证明

在这里插入图片描述

（3）例题

在这里插入图片描述

6. 频域微分特性

（1）定义

在这里插入图片描述

（2）证明

在这里插入图片描述

7. 时域积分特性

（1）定义

在这里插入图片描述

（2）例题

在这里插入图片描述

8. 频域积分特性

（1）定义

在这里插入图片描述

（2）例题

在这里插入图片描述

9. 卷积定理

卷积定理包括时域卷积定理与频域卷积定理，其核心是建立时域与频域卷积运算的映射关系。

（1）时域卷积定理

时域卷积定理表述为：两个信号在时域的卷积的傅里叶变换，等于两个信号各自傅里叶变换的乘积。利用该性质，可将复杂的时域卷积运算转换为简单的频域乘法运算。

定义：

在这里插入图片描述

证明：

在这里插入图片描述

（2）频域卷积定理

频域卷积定理表述为：两个信号在频域的卷积的傅里叶逆变换，等于两个信号各自的乘积。由于该过程可理解为一个信号对另一个信号的幅度进行调制，因此频域卷积定理也称为“幅度调制定理”。

定义：

在这里插入图片描述

例题：

在这里插入图片描述

10. 对称性

对称性（又称对偶性）表明：当时间变量 $t$ 与频率变量 $\omega$ 交换时，傅里叶变换与傅里叶逆变换的形式呈现对称关系。利用该性质可简化部分信号的傅里叶正变换与逆变换求解过程。

（1）定义

在这里插入图片描述

（2）证明

在这里插入图片描述

（3）例题

在这里插入图片描述

11. 帕塞瓦尔定理

（1）定义

在这里插入图片描述

（2）物理意义

非周期信号通常为能量信号（平均功率为零，总能量有限），其总能量 $W$ 可在时域表示为：

在这里插入图片描述

帕塞瓦尔定理的核心结论是：非周期信号在时域计算的总能量，与在频域计算的总能量相等。由于 $|F(j\omega)|^2$ 是 $\omega$ 的偶函数，总能量也可表示为：

在这里插入图片描述

关于傅里叶变换：时移与频移解读之解读

卓晴已于 2022-05-02 17:53:47 修改

一、简介

本文聚焦傅里叶变换中相互关联的三大核心特性——时移特性、频移特性与尺度特性。对《信号与系统》学科的深入理解，需结合经典理论推导、物理直观分析及数值计算验证三个维度，方可在工程应用中透过现象把握本质，建立对信号时域与频域映射关系的系统性认知。

关键词：快速傅里叶变换（FFT），时移特性，频移特性，尺度特性

00 背景

在西土城山羊卷的博文《傅里叶变换：时移与频移性质解读》中，其对傅里叶变换时移与频移特性的物理意义解读具有创新性，突破了传统教材中仅侧重数学推导的局限，为理解时域-频域关联提供了更直观的视角，本文将基于该视角展开进一步分析。

01 时移特性

傅里叶变换的时移特性表述为：若信号 $f (t)$ 在时域延迟 $t_0$ （ $t_0 \ge 0$ ），形成新信号 $f(t - t_0)$ ，则该延迟信号的傅里叶变换 $F_{t_0}(j\omega)$ 与原信号频谱 $F(j\omega)$ 的关系满足：

$F_{t_0}(j\omega) = F(j\omega) \cdot e^{-j\omega t_0}$

1.1 性质证明

时移特性的证明可通过傅里叶变换定义结合变量替换完成，具体步骤如下：

傅里叶变换定义：原信号 $f (t)$ 的傅里叶变换为

$F(j\omega) = \int_{-\infty}^{\infty} f(t) e^{-j\omega t} dt$
延迟信号的傅里叶变换：对延迟信号 $f(t - t_0)$ 代入变换定义，得

$F_{t_0}(j\omega) = \int_{-\infty}^{\infty} f(t - t_0) e^{-j\omega t} dt$
变量替换：令 $l = t - t_0$ ，则 $t = l + t_0$ ， $d t = d l$ ，积分上下限保持不变。代入上式得

$F_{t_0}(j\omega) = \int_{-\infty}^{\infty} f(l) e^{-j\omega (l + t_0)} dl$
分离指数项并化简：利用指数运算性质 $e^{-j\omega (l + t_0)} = e^{-j\omega l} \cdot e^{-j\omega t_0}$ ，将常数项 $e^{-j\omega t_0}$ 提出积分外，得

$F_{t_0}(j\omega) = e^{-j\omega t_0} \cdot \int_{-\infty}^{\infty} f(l) e^{-j\omega l} dl = F(j\omega) \cdot e^{-j\omega t_0}$

至此，时移特性得证。

1.2 物理解释

从上述公式可提取时移特性的两个核心物理意义：

幅度谱不变，相位谱附加线性相移：延迟仅影响信号的相位频谱，所有频率分量均叠加一个统一形式的负相位因子 $e^{-j\omega t_0}$ ，而幅度频谱 $|F(j\omega)|$ 保持不变。这表明时域延迟不改变信号的频率成分及各成分的相对强度。
相位延迟与频率成正比：附加相移的大小 $\Delta\phi(\omega) = -\omega t_0$ 与角频率 $\omega$ 呈线性关系，比例系数为 $t_0$ 。即频率越高的分量，其相位延迟越大。

1.2.1 特定信号举例

以由 4 个正弦分量叠加的信号为例，验证时移特性的物理意义。设信号表达式为：
$\sin(10t) + \sin(12t) + \sin(15t) + \sin(18t)$

该信号的时域波形及各频率分量波形如下图所示：

▲ 图 1.2.1 信号 f(t) 的四个频率分量

生成上述波形的 Python 代码如下：

from headm import *  # 导入自定义工具库

fdim = [10, 12, 15, 18]  # 四个正弦分量的角频率（rad/s）
t = linspace(0, 2, 1000)  # 时间序列：0~2s，共 1000 个采样点

plt.clf()
plt.figure(figsize=(10, 10))  # 设置画布尺寸

# 绘制叠加信号波形
plt.subplot(len(fdim) + 1, 1, 1)
sumsin = zeros(len(t))
for f in fdim:
    sumsin += sin(f * t)
plt.plot(t, sumsin, label=' 叠加信号 ')
plt.xlabel("时间 t (s)")
plt.ylabel("幅度")
plt.grid(True)
plt.legend()
plt.tight_layout()

# 绘制各频率分量波形
for idx, f in enumerate(fdim):
    plt.subplot(len(fdim) + 1, 1, idx + 2)
    plt.plot(t, sin(f * t), label=f'ω = {f} rad/s')
    plt.xlabel("时间 t (s)")
    plt.ylabel("幅度")
    plt.grid(True)
    plt.legend()
    plt.tight_layout()

plt.savefig(r"d:\temp\figure1.jpg")  # 保存图像
plt.close()
tspshowimage(image=r"d:\temp\figure1.jpg")  # 显示图像

若将信号延迟 $t_0 = 0.1 \, \text{s}$ ，得到延迟信号 $f (t - 0.1)$ ，其波形及各分量波形如下图所示：

▲ 图 1.2.2 延时信号对应的波形及其各个频率分量

从图中可直观观察到：

所有频率分量均延迟相同的时间 $t_0 = 0.1 \, \text{s}$ ，验证了“时域延迟是全局统一的”这一特性；
高频分量（如 $\omega = 18 \, \text{rad/s}$ ）的相位偏移更明显，符合“相位延迟与频率成正比”的规律。

下图进一步展示了不同典型信号（如矩形脉冲、正弦信号）经时域延迟后的频谱与相位变化，直观体现时移对相位谱的线性调制作用：

▲ 图 1.2.3 几种不同的典型信号平移后对应的频谱和相位

02 频移特性

频移特性是傅里叶变换中与时移特性对偶的核心性质，其工程应用（如调幅、解调）极为广泛。西土城山羊卷 对该特性的解读重点在于区分“频移”与“尺度变换”的本质差异，为工程应用提供了关键理论依据。

2.1 性质证明

频移特性表述为：若信号 $f (t)$ 的频谱 $F(j\omega)$ 在频域平移 $\omega_0$ ，形成新频谱 $F(j(\omega - \omega_0))$ ，则该频移频谱对应的时域信号 $f_{\omega_0}(t)$ 满足：
$f_{\omega_0}(t) = f(t) \cdot e^{j\omega_0 t}$

证明过程基于傅里叶逆变换定义，步骤如下：

傅里叶逆变换定义：原信号 $f (t)$ 由其频谱逆变换得到

$\frac{1}{2\pi} \int_{-\infty}^{\infty} F(j\omega) e^{j\omega t} d\omega$
频移频谱的逆变换：对频移频谱 $F(j(\omega - \omega_0))$ 代入逆变换定义，得

$f_{\omega_0}(t) = \frac{1}{2\pi} \int_{-\infty}^{\infty} F(j(\omega - \omega_0)) e^{j\omega t} d\omega$
变量替换：令 $\lambda = \omega - \omega_0$ ，则 $\omega = \lambda + \omega_0$ ， $d\omega = d\lambda$ ，积分上下限保持不变。代入上式得

$f_{\omega_0}(t) = \frac{1}{2\pi} \int_{-\infty}^{\infty} F(j\lambda) e^{j(\lambda + \omega_0)t} d\lambda$
分离指数项并化简：利用指数运算性质 $e^{j(\lambda + \omega_0)t} = e^{j\lambda t} \cdot e^{j\omega_0 t}$ ，将常数项 $e^{j\omega_0 t}$ 提出积分外，得

$f_{\omega_0}(t) = e^{j\omega_0 t} \cdot \frac{1}{2\pi} \int_{-\infty}^{\infty} F(j\lambda) e^{j\lambda t} d\lambda = f(t) \cdot e^{j\omega_0 t}$

至此，频移特性得证。

2.2 物理解释

频移特性的物理意义可从“时域调制-频域搬移”的对应关系展开：

时域调制对应频域搬移：时域中信号 $f (t)$ 与复振荡 $e^{j\omega_0 t}$ 的乘积，本质是对 $e^{j\omega_0 t}$ 进行幅度调制（ $f (t)$ 为调制信号， $e^{j\omega_0 t}$ 为载波），调制结果在频域表现为原频谱 $F(j\omega)$ 向 $\omega = \omega_0$ 方向整体搬移。
实载波调制的频谱对称搬移：工程中常用实正弦载波 $\cos(\omega_0 t)$ （而非复振荡 $e^{j\omega_0 t}$ ），利用欧拉公式 $\cos(\omega_0 t) = \frac{1}{2}(e^{j\omega_0 t} + e^{-j\omega_0 t})$ 可知，此时频谱会向 $\omega = \omega_0$ 和 $\omega = -\omega_0$ 两个方向对称搬移，形成“上边带”与“下边带”，这是调幅通信的核心原理。

下图展示了信号频谱搬移与时域调制的对应过程，直观体现频移特性的工程意义：

▲ 图 2.2.1 信号频谱的搬移对应的信号调制过程

2.3 尺度变换对应的频率变化

西土城山羊卷 提出的关键疑问——“频谱搬移使频率升高，为何时域表现不是尺度压缩？”——需通过对比频移特性与尺度变换特性的本质差异解答。

（1）尺度变换特性的核心规律

若信号 $f (t)$ 在时域发生尺度变换，形成新信号 $f (a t)$ （ $\neq 0$ ），则其傅里叶变换满足：

$\mathcal{F}\{f(a t)\} = \frac{1}{|a|} F\left(j \cdot \frac{\omega}{a}\right)$

该特性的物理意义为：

当 $a > 1$ 时，时域信号压缩，频域频谱展宽且幅度降低（频率升高）；
当 $0 < a < 1$ 时，时域信号展宽，频域频谱压缩且幅度升高（频率降低）；
当 $a < 0$ 时，信号在时域反转，同时伴随上述尺度变换效应。

（2）频移与尺度变换的本质差异

对比维度	频移特性（ $\cdot e^{j\omega_0 t}$ ）	尺度变换特性（ $f (a t)$ ）
时域表现	信号幅度被复载波调制，波形周期不变	信号波形被压缩/展宽，周期改变
频域表现	频谱整体搬移，带宽不变	频谱展宽/压缩，带宽改变
频率分量变化	各频率分量的数值均增加 $\omega_0$ （偏移）	各频率分量的数值按比例 $1/ a$ 缩放
工程应用	调幅、解调、信号混频	信号采样率转换、时域压缩存储

下图展示了傅里叶变换尺度特性的时域-频域对应关系，清晰区分其与频移特性的差异：

▲ 图 2.3.1 傅里叶变换的尺度性质

变换总结

本文系统分析了傅里叶变换的时移特性、频移特性及尺度变换特性，三者的核心关联与差异可归纳为：

对偶性：时移特性（时域延迟→频域线性相移）与频移特性（频域搬移→时域复调制）呈对偶关系，均体现时域-频域的线性映射；
本质差异：频移是频谱的“整体偏移”，不改变带宽与频率分量比例；尺度变换是频谱的“缩放”，改变带宽与频率分量数值；
理解维度：对三大特性的掌握需结合“数学推导（严谨性）”“物理直观（现象解释）”“数值验证（工程落地）”，三者协同方可建立对信号时域-频域关系的深度认知，为后续滤波、调制、采样等工程应用奠定理论基础。

傅里叶变换：时移与频移性质解读

科历杨curlyoung 已于 2022-01-23 19:38:37 修改

一、时移性质

$\mathscr{F}[f(t - t_0)] = F(f)e^{-j2\pi ft_0}$

时域信号可以分解为无穷多个谐振信号。当信号在时域上有 $t_0$ 的时延后，所有的谐振信号也会有 $t_0$ 的时延。从上述表达式可以看出，不同频率成分的时延大小相同，但相位改变量与其频率有关。频率为 $f$ 的谐振成分的相位改变量为 $2\pi ft_0$ 。在相同时间下，高频成分的相位改变量自然更大。

相位改变量为负的原因：时域中本应在 0 时刻到达的信号被推迟到了 $t_0$ 时刻。相应地，各频率分量本应在 0 时刻的相位值也改到了 $t_0$ 时刻。而当前 0 时刻的相位落后于 $t_0$ 时刻，因此各频率成分的相位表现为落后而非超前，故有负值的附加相位。

二、频移性质

$\mathscr{F}[f(t)e^{j2\pi f_0t}] = F(f - f_0)$

该式右侧表明信号的频谱整体向右移动 $f_0$ ，即信号的频率提高。在时域上，信号的振荡速度加快，但这种加快并不表现为时域信号的压缩，因此并非 $f (t / ?)$ 的形式。实际上是将 $F (f)$ 从 0 频搬移到 $f_0$ 中心频率上，属于调制操作。因此时域应写作 $f(t)\cos2\pi f_0t$ ，由于现在是复数表示形式，所以写为 $f(t)e^{j2\pi f_0t}$ 。