张量运算 | 原理、分解与实现

原创已于 2025-10-06 21:15:38 修改 · 1k 阅读

9 ·

CC 4.0 BY-SA版权

文章标签：

#张量运算

于 2025-10-06 19:52:05 首次发布

mathematics 专栏收录该内容

191 篇文章

订阅专栏

注：本文为 “张量运算” 相关合辑。
略作重排，未全校去重。
如有内容异常，请看原文。

张量乘积的三种形式

QT-Smile已于 2022-01-19 21:15:17 修改

乘积类型	NumPy 实现方式	PyTorch 实现方式
对应点相乘（简称点乘）	`np.multiply(A, B)` 或 `A * B`	`A.mul(B)`
矩阵相乘（内积、点积）	`np.dot(A, B)`	`A.mm(B)`
直积或张量积（克罗内克积）	`np.kron(A, B)`	`A.kron(B)`

本文主要围绕以下三种乘积展开详细介绍：

矩阵乘积（Matmul Product）
哈达马积（Hadamard Product）
克罗内克积（Kronecker Product）

1. 矩阵乘积（Matmul Product）（内积、点积）—— $A.\text{mm}(B)$

设 $A$ 为 $\times p$ 矩阵， $B$ 为 $\times n$ 矩阵，则称 $\times n$ 矩阵 $C$ 为矩阵 $A$ 与 $B$ 的乘积，记作 $C = A B$ 。其中，矩阵 $C$ 中第 $i$ 行第 $j$ 列元素可表示为：
$(AB)_{ij} = \sum_{k=1}^{p} a_{ik} b_{kj} = a_{i1} b_{1j} + a_{i2} b_{2j} + \cdots + a_{ip} b_{pj}$

示例

$\begin{pmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \end{pmatrix} \begin{pmatrix} 1 & 4 \\ 2 & 5 \\ 3 & 6 \end{pmatrix} = \begin{pmatrix} 1 \times 1 + 2 \times 2 + 3 \times 3 & 1 \times 4 + 2 \times 5 + 3 \times 6 \\ 4 \times 1 + 5 \times 2 + 6 \times 3 & 4 \times 4 + 5 \times 5 + 6 \times 6 \end{pmatrix} = \begin{pmatrix} 14 & 32 \\ 32 & 77 \end{pmatrix}$

代码实现（PyTorch）

import torch
a = list()
b = list()
for i in range(3):
    a.append([])
    b.append([])
    for j in range(4):
        a[i].append(i)
        b[i].append(i * 2)
a = torch.tensor(a)
b = torch.tensor(b)
b = b.t()
print(a)
print(b)
c = a.mm(b)
print(c)

运行结果

tensor([[0, 0, 0, 0],
        [1, 1, 1, 1],
        [2, 2, 2, 2]])
tensor([[0, 2, 4],
        [0, 2, 4],
        [0, 2, 4],
        [0, 2, 4]])
tensor([[ 0,  0,  0],
        [ 0,  8, 16],
        [ 0, 16, 32]])

2. 哈达马积（Hadamard Product）（两张量维度需一致，对应点相乘）—— $A.\text{mul}(B)$

$\times n$ 矩阵 $A$ 与 $\times n$ 矩阵 $B$ 的哈达马积记为 $A * B$ ，其元素定义为两个矩阵对应元素的乘积。

定义

设 $\in \mathbb{C}^{m \times n}$ ，且 $A = [a_{ij}]$ ， $B = [b_{ij}]$ ，则哈达马积为 $\times n$ 矩阵：
$\begin{bmatrix} a_{11}b_{11} & a_{12}b_{12} & \cdots & a_{1n}b_{1n} \\ a_{21}b_{21} & a_{22}b_{22} & \cdots & a_{2n}b_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{m1}b_{m1} & a_{m2}b_{m2} & \cdots & a_{mn}b_{mn} \end{bmatrix}$

示例

$\begin{pmatrix} 1 & 3 & 2 \\ 1 & 0 & 0 \\ 1 & 2 & 2 \end{pmatrix} * \begin{pmatrix} 0 & 0 & 2 \\ 7 & 5 & 0 \\ 2 & 1 & 1 \end{pmatrix} = \begin{pmatrix} 1 \cdot 0 & 3 \cdot 0 & 2 \cdot 2 \\ 1 \cdot 7 & 0 \cdot 5 & 0 \cdot 0 \\ 1 \cdot 2 & 2 \cdot 1 & 2 \cdot 1 \end{pmatrix} = \begin{pmatrix} 0 & 0 & 4 \\ 7 & 0 & 0 \\ 2 & 2 & 2 \end{pmatrix}$

代码实现（PyTorch）

import torch

a = list()
b = list()
for i in range(3):
    a.append([])
    b.append([])
    for j in range(4):
        a[i].append(i)
        b[i].append(i * 2)

a = torch.tensor(a)
b = torch.tensor(b)
print(a)
print(b)

c = a.mul(b)
print(c)

运行结果

tensor([[0, 0, 0, 0],
        [1, 1, 1, 1],
        [2, 2, 2, 2]])
tensor([[0, 0, 0, 0],
        [2, 2, 2, 2],
        [4, 4, 4, 4]])
tensor([[0, 0, 0, 0],
        [2, 2, 2, 2],
        [8, 8, 8, 8]])

3. 克罗内克积（Kronecker Product）—— $A.\text{kron}(B)$

克罗内克积是两个任意大小矩阵间的运算，又称为直积或张量积，记为 $\otimes B$ 。

定义

设 $\in \mathbb{R}^{m \times n}$ ， $\in \mathbb{R}^{p \times q}$ ，则克罗内克积定义为：
$\otimes B = \begin{bmatrix} a_{11}B & \cdots & a_{1n}B \\ a_{21}B & \cdots & a_{2n}B \\ \vdots & \ddots & \vdots \\ a_{m1}B & \cdots & a_{mn}B \end{bmatrix}$
更具体地可表示为：
$\otimes B = \begin{bmatrix} a_{11}b_{11} & a_{11}b_{12} & \cdots & a_{11}b_{1q} & \cdots & a_{1n}b_{11} & a_{1n}b_{12} & \cdots & a_{1n}b_{1q} \\ a_{11}b_{21} & a_{11}b_{22} & \cdots & a_{11}b_{2q} & \cdots & a_{1n}b_{21} & a_{1n}b_{22} & \cdots & a_{1n}b_{2q} \\ \vdots & \vdots & \ddots & \vdots & & \vdots & \vdots & \ddots & \vdots \\ a_{11}b_{p1} & a_{11}b_{p2} & \cdots & a_{11}b_{pq} & \cdots & a_{1n}b_{p1} & a_{1n}b_{p2} & \cdots & a_{1n}b_{pq} \\ \vdots & \vdots & \vdots & \ddots & \vdots & \vdots & \vdots & \vdots & \vdots \\ a_{m1}b_{11} & a_{m1}b_{12} & \cdots & a_{m1}b_{1q} & \cdots & a_{mn}b_{11} & a_{mn}b_{12} & \cdots & a_{mn}b_{1q} \\ a_{m1}b_{21} & a_{m1}b_{22} & \cdots & a_{m1}b_{2q} & \cdots & a_{mn}b_{21} & a_{mn}b_{22} & \cdots & a_{mn}b_{2q} \\ \vdots & \vdots & \ddots & \vdots & & \vdots & \vdots & \ddots & \vdots \\ a_{m1}b_{p1} & a_{m1}b_{p2} & \cdots & a_{m1}b_{pq} & \cdots & a_{mn}b_{p1} & a_{mn}b_{p2} & \cdots & a_{mn}b_{pq} \end{bmatrix}$

示例 1

$\begin{pmatrix} 1 & 2 \\ 3 & 1 \end{pmatrix} \otimes \begin{pmatrix} 0 & 3 \\ 2 & 1 \end{pmatrix} = \begin{pmatrix} 1 \cdot 0 & 1 \cdot 3 & 2 \cdot 0 & 2 \cdot 3 \\ 1 \cdot 2 & 1 \cdot 1 & 2 \cdot 2 & 2 \cdot 1 \\ 3 \cdot 0 & 3 \cdot 3 & 1 \cdot 0 & 1 \cdot 3 \\ 3 \cdot 2 & 3 \cdot 1 & 1 \cdot 2 & 1 \cdot 1 \end{pmatrix} = \begin{pmatrix} 0 & 3 & 0 & 6 \\ 2 & 1 & 4 & 2 \\ 0 & 9 & 0 & 3 \\ 6 & 3 & 2 & 1 \end{pmatrix}$

示例 2

$\begin{pmatrix} a_{11} & a_{12} \\ a_{21} & a_{22} \\ a_{31} & a_{32} \end{pmatrix} \otimes \begin{pmatrix} b_{11} & b_{12} & b_{13} \\ b_{21} & b_{22} & b_{23} \end{pmatrix} = \begin{bmatrix} a_{11}b_{11} & a_{11}b_{12} & a_{11}b_{13} & a_{12}b_{11} & a_{12}b_{12} & a_{12}b_{13} \\ a_{11}b_{21} & a_{11}b_{22} & a_{11}b_{23} & a_{12}b_{21} & a_{12}b_{22} & a_{12}b_{23} \\ a_{21}b_{11} & a_{21}b_{12} & a_{21}b_{13} & a_{22}b_{11} & a_{22}b_{12} & a_{22}b_{13} \\ a_{21}b_{21} & a_{21}b_{22} & a_{21}b_{23} & a_{22}b_{21} & a_{22}b_{22} & a_{22}b_{23} \\ a_{31}b_{11} & a_{31}b_{12} & a_{31}b_{13} & a_{32}b_{11} & a_{32}b_{12} & a_{32}b_{13} \\ a_{31}b_{21} & a_{31}b_{22} & a_{31}b_{23} & a_{32}b_{21} & a_{32}b_{22} & a_{32}b_{23} \end{bmatrix}$

代码实现（PyTorch）

```python
import torch
a = list()
b = list()
for i in range(2):
    a.append([])
    b.append([])
    for j in range(2):
        a[i].append(i)
        b[i].append(i * 2)
a = torch.tensor(a)
b = torch.tensor(b)
print(a)
print(b)
c = a.kron(b)
print(c)

运行结果

tensor([[0, 0],
        [1, 1]])
tensor([[0, 0],
        [2, 2]])
tensor([[0, 0, 0, 0],
        [0, 0, 0, 0],
        [0, 0, 0, 0],
        [2, 2, 2, 2]])

张量学习：张量乘积

计算机量子狗已于 2022-03-07 08:39:26 修改

一、向量的外积

1.1 实例一

已知三个向量：
$\vec{u} = \begin{bmatrix} u_1 \\ u_2 \end{bmatrix}, \quad \vec{v} = \begin{bmatrix} v_1 \\ v_2 \\ v_3 \end{bmatrix}, \quad \vec{w} = \begin{bmatrix} w_1 \\ w_2 \end{bmatrix}$
将三个向量进行外积运算：
$\mathcal{X} = \vec{u} \otimes \vec{v} \otimes \vec{w}$

其结果是一个高维向量，各分量为三个向量对应分量的乘积组合。

其展开形式为：
$\mathcal{X} = \begin{bmatrix} u_1 v_1 w_1 \\ u_2 v_1 w_1 \\ u_1 v_1 w_2 \\ u_2 v_1 w_2 \\ u_1 v_2 w_1 \\ u_2 v_2 w_1 \\ u_1 v_2 w_2 \\ u_2 v_2 w_2 \\ u_1 v_3 w_1 \\ u_2 v_3 w_1 \\ u_1 v_3 w_2 \\ u_2 v_3 w_2 \end{bmatrix}$

简言之，张量积运算会将多个向量的分量进行“全组合相乘”，生成一个包含所有分量乘积组合的高维结构。

作用：显著降低参数维度（将原本需存储的 12 个参数降低为 7 个独立参数)。

1.2 实例二

已知三个向量：
$\vec{a} = (1, 2)^T, \quad \vec{b} = (3, 4)^T, \quad \vec{c} = (5, 6, 7)^T$
对其进行外积运算 $\mathcal{X} = \vec{a} \otimes \vec{b} \otimes \vec{c}$ ，结果可按 $\vec{c}$ 的维度分解为三个矩阵：

当 $\vec{c}$ 取第一个元素 $5$ 时：
$\mathcal{X}(:, :, 1) = \begin{bmatrix} 1 \times 3 \times 5 & 1 \times 4 \times 5 \\ 2 \times 3 \times 5 & 2 \times 4 \times 5 \end{bmatrix} = \begin{bmatrix} 15 & 20 \\ 30 & 40 \end{bmatrix}$
当 $\vec{c}$ 取第二个元素 $6$ 时：
$\mathcal{X}(:, :, 2) = \begin{bmatrix} 1 \times 3 \times 6 & 1 \times 4 \times 6 \\ 2 \times 3 \times 6 & 2 \times 4 \times 6 \end{bmatrix} = \begin{bmatrix} 18 & 24 \\ 36 & 48 \end{bmatrix}$
当 $\vec{c}$ 取第三个元素 $7$ 时：
$\mathcal{X}(:, :, 3) = \begin{bmatrix} 1 \times 3 \times 7 & 1 \times 4 \times 7 \\ 2 \times 3 \times 7 & 2 \times 4 \times 7 \end{bmatrix} = \begin{bmatrix} 21 & 28 \\ 42 & 56 \end{bmatrix}$

二、张量内积

设两个同维度张量 $\mathcal{A}$ 和 $\mathcal{B}$ ，其中 $\mathcal{A} = [a_1, a_2, a_3, a_4, a_5, a_6, a_7, a_8]$ ， $\mathcal{B} = [b_1, b_2, b_3, b_4, b_5, b_6, b_7, b_8]$ ，则它们的内积定义为对应元素乘积之和：
$\langle \mathcal{A}, \mathcal{B} \rangle = a_1 b_1 + a_2 b_2 + a_3 b_3 + a_4 b_4 + a_5 b_5 + a_6 b_6 + a_7 b_7 + a_8 b_8$

三、张量积（直积）

定义：对于两个任意阶张量，将第一个张量的每个分量与第二个张量的每个分量相乘，所得组合的集合仍为一个张量，该张量称为两个原张量的张量积（积张量）。
阶数性质：张量积的阶数等于两个因子张量阶数之和。例如，1 阶张量 $a_i$ 与 2 阶张量 $b_{jk}$ 的张量积为 3 阶张量 $c_{ijk} = a_i b_{jk}$ 。

示例

设 1 阶张量 $a_i = [a_1, a_2, a_3]$ ，1 阶张量 $b_j = [b_1, b_2, b_3]$ ，则它们的张量积为 2 阶张量：
$a_i \otimes b_j = \begin{bmatrix} a_1 b_1 & a_1 b_2 & a_1 b_3 \\ a_2 b_1 & a_2 b_2 & a_2 b_3 \\ a_3 b_1 & a_3 b_2 & a_3 b_3 \end{bmatrix}$

四、克罗内克积（Kronecker Product）

设矩阵 $\in \mathbb{R}^{I \times J}$ ， $\in \mathbb{R}^{K \times L}$ ，则克罗内克积定义为：
$\otimes B = \begin{bmatrix} a_{11}B & a_{12}B & \cdots & a_{1J}B \\ a_{21}B & a_{22}B & \cdots & a_{2J}B \\ \vdots & \vdots & \ddots & \vdots \\ a_{I1}B & a_{I2}B & \cdots & a_{IJ}B \end{bmatrix} \in \mathbb{R}^{IK \times JL}$

示例

五、哈达马积（Hadamard Product）

设矩阵 $\in \mathbb{R}^{I \times J}$ ， $\in \mathbb{R}^{I \times J}$ （两矩阵维度需一致），则哈达马积定义为：
$\begin{bmatrix} a_{11}b_{11} & a_{12}b_{12} & \cdots & a_{1J}b_{1J} \\ a_{21}b_{21} & a_{22}b_{22} & \cdots & a_{2J}b_{2J} \\ \vdots & \vdots & \ddots & \vdots \\ a_{I1}b_{I1} & a_{I2}b_{I2} & \cdots & a_{IJ}b_{IJ} \end{bmatrix} \in \mathbb{R}^{I \times J}$

六、卡特里-拉奥积（Khatri-Rao Product）

设矩阵 $\in \mathbb{R}^{I \times K}$ ， $\in \mathbb{R}^{J \times K}$ （两矩阵列数需一致），记 $(\vec{a}_1, \vec{a}_2, \cdots, \vec{a}_K)$ （ $\vec{a}_k$ 为 $A$ 的第 $k$ 列向量）， $(\vec{b}_1, \vec{b}_2, \cdots, \vec{b}_K)$ （ $\vec{b}_k$ 为 $B$ 的第 $k$ 列向量），则卡特里-拉奥积定义为：
$\odot B = \begin{bmatrix} \vec{a}_1 \otimes \vec{b}_1 & \vec{a}_2 \otimes \vec{b}_2 & \cdots & \vec{a}_K \otimes \vec{b}_K \end{bmatrix} \in \mathbb{R}^{IJ \times K}$

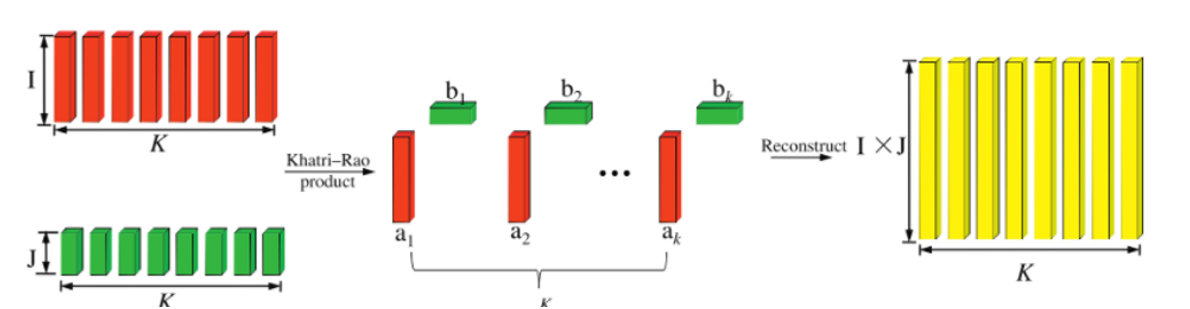
在这里插入图片描述

示例

设矩阵 $\begin{pmatrix} 1 & 2 \\ 3 & 4 \end{pmatrix} = (\vec{a}_1, \vec{a}_2)$ ，其中 $\vec{a}_1 = \begin{bmatrix} 1 \\ 3 \end{bmatrix}$ ， $\vec{a}_2 = \begin{bmatrix} 2 \\ 4 \end{bmatrix}$ ；

矩阵 $\begin{pmatrix} 5 & 6 \\ 7 & 8 \\ 9 & 10 \end{pmatrix} = (\vec{b}_1, \vec{b}_2)$ ，其中 $\vec{b}_1 = \begin{bmatrix} 5 \\ 7 \\ 9 \end{bmatrix}$ ， $\vec{b}_2 = \begin{bmatrix} 6 \\ 8 \\ 10 \end{bmatrix}$ 。

则卡特里-拉奥积为：
$\odot B = \begin{bmatrix} \vec{a}_1 \otimes \vec{b}_1 & \vec{a}_2 \otimes \vec{b}_2 \end{bmatrix} = \begin{bmatrix} 1 \times 5 & 2 \times 6 \\ 1 \times 7 & 2 \times 8 \\ 1 \times 9 & 2 \times 10 \\ 3 \times 5 & 4 \times 6 \\ 3 \times 7 & 4 \times 8 \\ 3 \times 9 & 4 \times 10 \end{bmatrix} = \begin{bmatrix} 5 & 12 \\ 7 & 16 \\ 9 & 20 \\ 15 & 24 \\ 21 & 32 \\ 27 & 40 \end{bmatrix}$

七、张量乘法

张量乘法可分为以下三种类型：

同维度张量相乘（如张量内积）
张量与矩阵相乘
张量与向量相乘

7.1 张量内积

设两个同维度张量 $\mathcal{A}$ 和 $\mathcal{B}$ ，则其内积定义为：
$\langle \mathcal{A}, \mathcal{B} \rangle = \sum_{k=1}^{n} a_k b_k$

示例

$\mathcal{A} = \begin{matrix} & & a_5 & a_6 \\ & & a_7 & a_8 \\ a_1 & a_2 \\ a_3 & a_4 \\ \end{matrix}$

$\mathcal{B} = \begin{matrix} & & b_5 & b_6 \\ & & b_7 & b_8 \\ b_1 & b_2 \\ b_3 & b_4 \\ \end{matrix}$

则：
$\langle \mathcal{A}, \mathcal{B} \rangle = a_1 b_1 + a_2 b_2 + a_3 b_3 + a_4 b_4 + a_5 b_5 + a_6 b_6 + a_7 b_7 + a_8 b_8$

7.2 张量乘以矩阵

张量乘以矩阵步骤如下：

将张量矩阵化
再将张量和矩阵相乘

张量的 Mode - 1 矩阵化（Matricization）示例

假设有一个张量 $\mathcal{T}$ 和一个矩阵 $\mathbf{A}$ ：

张量 $\mathcal{T}$

$\mathcal{T} = \begin{matrix} & & 5 & 6 \\ & & 7 & 8 \\ 1 & 2 \\ 3 & 4 \\ \end{matrix}$

矩阵 $\mathbf{A}$

$\mathbf{A} = \begin{pmatrix} a & b \\ c & d \end{pmatrix}$

对张量进行 Mode - 1 Matricization（模式 1 矩阵化）

将张量 $\mathcal{T}$ 按模式 1 展开为矩阵 $\mathcal{T}_{(1)}$ ，结果为：
$\mathcal{T}_{(1)} = \begin{pmatrix} 1 & 2 & 5 & 6 \\ 3 & 4 & 7 & 8 \end{pmatrix}$
（ $\mathcal{T}_{(1)}$ 表示张量 $\mathcal{T}$ 按 mode-1 展开后的矩阵）

张量与矩阵的模式 - 1 乘积运算

接着，将通过 Mode - 1 Matricization 得到的矩阵 $\mathcal{T}_{(1)}$ 与矩阵 $\mathbf{A}$ 相乘：

运算表达式

张量 $\mathcal{T}$ 与矩阵 $\mathbf{A}$ 的模式 - 1 乘积（记为 $\mathcal{P} = \mathcal{T} \times_1 \mathbf{A}$ ），对应到矩阵化后的运算为 $\mathcal{P}_{(1)} = \mathbf{A}\mathcal{T}_{(1)}$ ，其中：

$\mathbf{A} = \begin{pmatrix} a & b \\ c & d \end{pmatrix}, \quad \mathcal{T}_{(1)} = \begin{pmatrix} 1 & 2 & 5 & 6 \\ 3 & 4 & 7 & 8 \end{pmatrix}$
其中， $\mathcal{P} = \mathcal{T} \times_1 A$ 表示张量 $\mathcal{T}$ 沿 mode-1 方向与矩阵 $A$ 相乘， $\mathcal{P}_{(1)}$ 为结果张量 $\mathcal{P}$ 按 mode-1 展开后的矩阵。

矩阵乘法展开

按照矩阵乘法规则（行乘列，对应元素相乘后求和），计算 $\mathbf{A}\mathcal{T}_{(1)}$ ：

$\begin{align*} \mathcal{P}=\mathcal{T}{{\times }_{1}}\mathbf{A}\rightsquigarrow {{\mathcal{P}}_{(1)}} & =\mathbf{A}{{\mathcal{T}}_{(1)}} \\ & =\left( \begin{matrix} a & b \\ c & d \\ \end{matrix} \right)\left( \begin{matrix} 1 & 2 & 5 & 6 \\ 3 & 4 & 7 & 8 \\ \end{matrix} \right) \\ &= \begin{pmatrix} a \times 1 + b \times 3 & a \times 2 + b \times 4 & a \times 5 + b \times 7 & a \times 6 + b \times 8 \\ c \times 1 + d \times 3 & c \times 2 + d \times 4 & c \times 5 + d \times 7 & c \times 6 + d \times 8 \end{pmatrix} \\ & =\left( \begin{matrix} a+3b & 2a+4b & 5a+7b & 6a+8b \\ c+3d & 2c+4d & 5c+7d & 6c+8d \\ \end{matrix} \right) \end{align*}$

结果张量结构示意

若将乘积结果还原为张量的层级结构（示意形式）：

$\begin{matrix} & & 5c + 7d & 6c + 8d \\ & & 5a + 7b & 6a + 8b \\ a + 3b & 2a + 4b \\ c + 3d & 2c + 4d \\ \end{matrix}$

其过程可以用一个图演示：
在这里插入图片描述

张量运算符号

张量相关

$\mathcal{T}$ ：表示张量，三维及以上的高维结构，通过分块嵌套形式展示其多维度分量布局。
$\mathcal{T}_{(1)}$ ：表示对张量 $\mathcal{T}$ 进行模式 - 1 矩阵化（Mode - 1 Matricization） 后得到的矩阵。
模式 - 1 矩阵化是将张量的第 1 个维度展开，转化为二维矩阵，便于与普通矩阵进行乘法运算。
$\mathcal{P}$ ：表示张量 $\mathcal{T}$ 与矩阵 $\mathbf{A}$ 进行模式 - 1 乘积运算后得到的新张量。
$\mathcal{P}_{(1)}$ ：表示对新张量 $\mathcal{P}$ 进行模式 - 1 矩阵化后得到的矩阵。

矩阵相关

$\mathbf{A}$ ：表示普通矩阵（二维数组），参与张量与矩阵的模式乘积运算。

运算相关

$\times_1$ ：表示张量与矩阵的模式 - 1 乘积运算。该运算针对张量的第 1 个维度，通过先对张量进行模式 - 1 矩阵化，再与矩阵做普通矩阵乘法，最后还原为张量的方式进行。
矩阵乘法（无特殊标注时的乘法）表示普通的矩阵乘法，遵循“行乘列，对应元素相乘后求和”的规则，用于矩阵化后的张量（即矩阵形式）与普通矩阵之间的运算。
$\rightsquigarrow$ ：在数学和科学文献中通常用来表示一个映射（mapping）或者变换（transformation），从一个对象或状态到另一个对象或状态的过程，但与等号 $=$ 不同，它强调的是一个方向性的过程，而不是简单的等价关系。

八、总结与思考

张量的各类乘积（如张量积、克罗内克积、哈达马积等）与矩阵乘积存在部分对应关系，其具体物理意义需在实际应用场景（如量子力学、信号处理、机器学习）中进一步体现。掌握张量乘积的定义、性质及计算方法，是处理多维数据和复杂系统的关键基础。

如何理解与实现「张量展开」

Xinyu Chen 编辑于 2023-01-21 06:44

张量展开（tensor unfolding）是张量计算的核心组成部分。在实际计算中，为简化高阶张量的运算流程，将其展开为矩阵（即矩阵化（matricization））是常用手段。然而，由于高阶张量矩阵化过程涉及多维度结构的重组，该过程具有较强的抽象性，导致张量展开成为张量计算领域的核心理解难点之一。

1. 张量的定义与结构

为后续理解张量展开的原理，首先明确张量的基本定义与结构。对于一个 $d$ 阶张量 $\mathcal{X}$ ，其数学表示为 $\mathcal{X} \in \mathbb{R}^{n_1 \times n_2 \times \cdots \times n_d}$ ，其中 $n_1, n_2, \dots, n_d$ 分别表示张量在各维度上的尺寸。

图 1 展示了从标量（scalar，0 阶张量）、向量（vector，1 阶张量）、矩阵（matrix，2 阶张量）到三阶张量的结构示意，直观呈现了张量维度的递进关系。

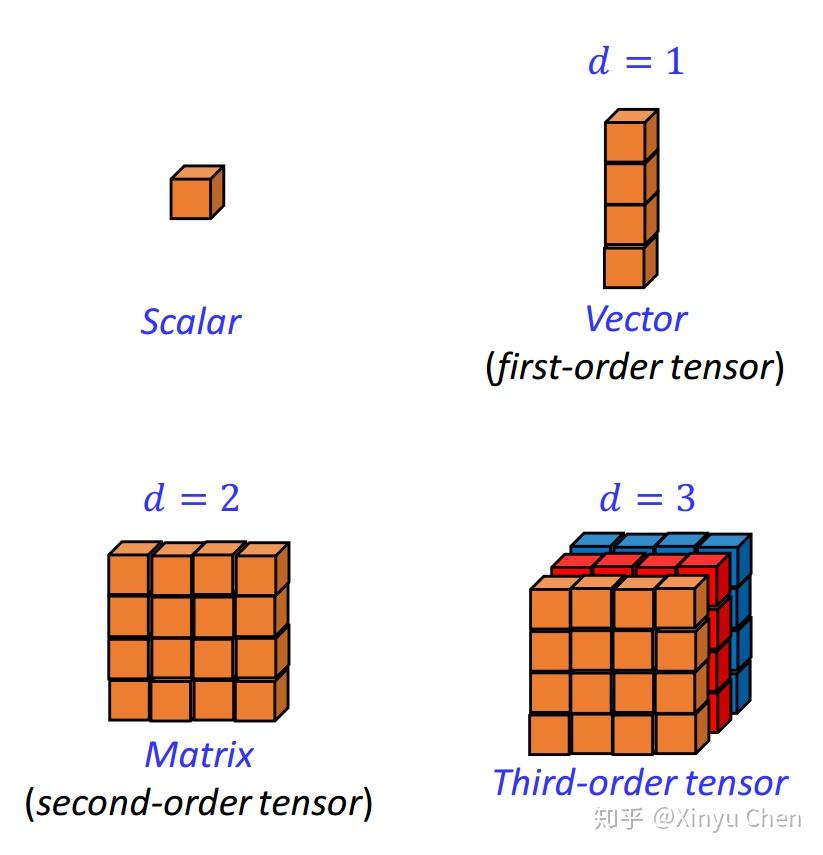
在这里插入图片描述

图 1 从标量到高阶张量的结构示意

以三阶张量 $\mathcal{X} \in \mathbb{R}^{n_1 \times n_2 \times n_3}$ 为例，其可沿三个不同维度进行切割，得到三类切片（slice），具体结构如图 2 所示。切片是理解张量展开的关键中间结构，后续展开操作需基于切片的重组实现。

在这里插入图片描述

图 2 三阶张量的切片示意

2. 张量展开的数学定义

与仅含行、列两个维度的矩阵不同，三阶张量包含三个模态（mode），每个模态对应一个展开方向。沿不同模态展开时，需将张量的对应维度作为展开后矩阵的行，并将剩余维度重组为矩阵的列，最终得到不同维度的矩阵。以下为三阶张量各模态展开的数学表达式：

2.1 模态 1 展开（mode-1 unfolding）

沿模态 1 展开时，以张量的第一个维度（尺寸 $n_1$ ）作为展开矩阵的行，剩余两个维度（尺寸 $n_2, n_3$ ）重组为列（总列数 $n_2 \times n_3$ ），数学表达式为：
$\mathcal{X}_{(1)} = \left[\mathcal{X}(:,:,1), \mathcal{X}(:,:,2), \dots, \mathcal{X}(:,:,n_3)\right] \in \mathbb{R}^{n_1 \times (n_2 n_3)}$
其中 $\mathcal{X}(:,:,i)$ （ $i=1,2,\dots,n_3$ ）表示张量沿第三个维度的第 $i$ 个切片。

2.2 模态 2 展开（mode-2 unfolding）

沿模态 2 展开时，以张量的第二个维度（尺寸 $n_2$ ）作为展开矩阵的行，剩余两个维度（尺寸 $n_1, n_3$ ）重组为列（总列数 $n_1 \times n_3$ ），且需对每个切片进行转置，数学表达式为：
$\mathcal{X}_{(2)} = \left[\mathcal{X}(:,:,1)^T, \mathcal{X}(:,:,2)^T, \dots, \mathcal{X}(:,:,n_3)^T\right] \in \mathbb{R}^{n_2 \times (n_1 n_3)}$

2.3 模态 3 展开（mode-3 unfolding）

沿模态 3 展开时，以张量的第三个维度（尺寸 $n_3$ ）作为展开矩阵的行，剩余两个维度（尺寸 $n_1, n_2$ ）重组为列（总列数 $n_1 \times n_2$ ），且需对每个切片（沿第二个维度）进行转置，数学表达式为：
$\mathcal{X}_{(3)} = \left[\mathcal{X}(:,1,:)^T, \mathcal{X}(:,2,:)^T, \dots, \mathcal{X}(:,n_2,:)^T\right] \in \mathbb{R}^{n_3 \times (n_1 n_2)}$

结合图 2 中三阶张量的切片结构，图 3 给出了各模态展开的直观示意图，清晰展示了切片重组为矩阵的过程。

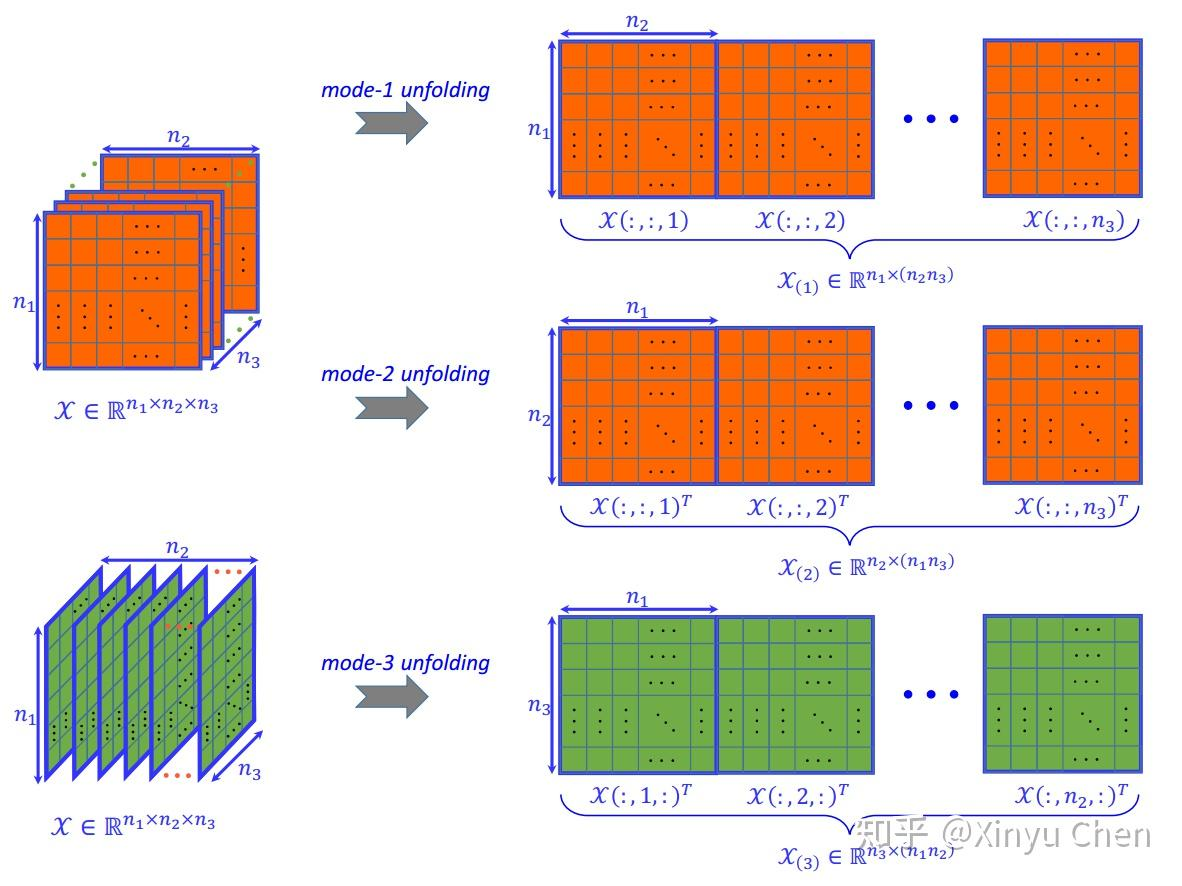
在这里插入图片描述

图 3 三阶张量各模态展开的示意图

3. 张量展开的实例分析

以具体三阶张量为例，验证上述展开规则的正确性。设三阶张量 $\mathcal{X} \in \mathbb{R}^{4 \times 3 \times 2}$ ，其沿第三个维度的两个切片分别为：
$\mathcal{X}(:,:,1) = \begin{bmatrix} x_{111} & x_{121} & x_{131} \\ x_{211} & x_{221} & x_{231} \\ x_{311} & x_{321} & x_{331} \\ x_{411} & x_{421} & x_{431} \end{bmatrix}, \quad \mathcal{X}(:,:,2) = \begin{bmatrix} x_{112} & x_{122} & x_{132} \\ x_{212} & x_{222} & x_{232} \\ x_{312} & x_{322} & x_{332} \\ x_{412} & x_{422} & x_{432} \end{bmatrix}$

3.1 模态 1 展开结果

根据模态 1 展开规则，直接将两个切片按列拼接，得到展开矩阵：
$\mathcal{X}_{(1)} = \begin{bmatrix} x_{111} & x_{121} & x_{131} & x_{112} & x_{122} & x_{132} \\ x_{211} & x_{221} & x_{231} & x_{212} & x_{222} & x_{232} \\ x_{311} & x_{321} & x_{331} & x_{312} & x_{322} & x_{332} \\ x_{411} & x_{421} & x_{431} & x_{412} & x_{422} & x_{432} \end{bmatrix}$
该矩阵尺寸为 $\times 6$ ，符合 $\mathbb{R}^{n_1 \times (n_2 n_3)} = \mathbb{R}^{4 \times (3 \times 2)}$ 的维度要求。

3.2 模态 2 展开结果

根据模态 2 展开规则，先对两个切片分别转置，再按列拼接，得到展开矩阵：
$\mathcal{X}_{(2)} = \begin{bmatrix} x_{111} & x_{211} & x_{311} & x_{411} & x_{112} & x_{212} & x_{312} & x_{412} \\ x_{121} & x_{221} & x_{321} & x_{421} & x_{122} & x_{222} & x_{322} & x_{422} \\ x_{131} & x_{231} & x_{331} & x_{431} & x_{132} & x_{232} & x_{332} & x_{432} \end{bmatrix}$
该矩阵尺寸为 $\times 8$ ，符合 $\mathbb{R}^{n_2 \times (n_1 n_3)} = \mathbb{R}^{3 \times (4 \times 2)}$ 的维度要求。

3.3 模态 3 展开练习

读者可自行验证：沿模态 3 展开时，需先获取张量沿第二个维度的切片（ $\mathcal{X}(:,1,:), \mathcal{X}(:,2,:), \mathcal{X}(:,3,:)$ ），对每个切片转置后按列拼接，最终得到尺寸为 $\times 12$ （即 $\mathbb{R}^{n_3 \times (n_1 n_2)} = \mathbb{R}^{2 \times (4 \times 3)}$ ）的矩阵。

4. MATLAB 环境下的张量展开实现

在 MATLAB 中，可基于内置函数 permute（维度重排）和 reshape（矩阵重塑）设计通用张量展开函数，无需依赖外部工具箱。该函数支持任意阶数张量的展开，输入参数与功能说明如下：

参数	类型	功能说明
`ten`	张量	待展开的任意阶数张量，数学表示为 $\mathcal{X} \in \mathbb{R}^{n_1 \times n_2 \times \cdots \times n_d}$
`dim`	向量	张量各维度的尺寸，即 $\text{dim} = (n_1, n_2, \dots, n_d)$
`k`	标量	指定的展开模态，取值范围为 $\dots, d$
`mat`	矩阵	输出的展开矩阵，维度由展开模态决定

4.1 函数定义

function mat = ten2mat(ten, dim, k)
    % 功能：将任意阶数张量沿指定模态展开为矩阵
    % 输入：
    %   ten - 待展开张量，维度为 n1×n2×…×nd
    %   dim - 张量各维度尺寸向量，dim = (n1, n2, …, nd)
    %   k   - 展开模态，1 ≤ k ≤ d
    % 输出：
    %   mat - 展开后的矩阵
    
    % 步骤1：将指定模态 k 重排至第一个维度，其余维度按原顺序排列
    permuted_ten = permute(ten, [k, 1:k-1, k+1:length(dim)]);
    % 步骤2：将重排后的张量重塑为矩阵，行数为 dim(k)，列数自动计算
    mat = reshape(permuted_ten, dim(k), []);
end

4.2 函数调用示例

以尺寸为 $\times 3 \times 2$ 的张量为例（元素为 1 至 24 的连续整数），验证各模态展开结果：

构造测试张量

>> ten = reshape([1:24], [4, 3, 2]);  % 生成 4×3×2 的张量
>> ten(:,:,1)  % 查看沿第三个维度的第 1 个切片
ans =
     1     5     9
     2     6    10
     3     7    11
     4     8    12
>> ten(:,:,2)  % 查看沿第三个维度的第 2 个切片
ans =
    13    17    21
    14    18    22
    15    19    23
    16    20    24

模态 1 展开

>> ten2mat(ten, [4, 3, 2], 1)  % 沿模态 1 展开
ans =
     1     5     9    13    17    21
     2     6    10    14    18    22
     3     7    11    15    19    23
     4     8    12    16    20    24

结果与 3.1 节理论推导一致，尺寸为 $\times 6$ 。

模态 2 展开

>> ten2mat(ten, [4, 3, 2], 2)  % 沿模态 2 展开
ans =
     1     2     3     4    13    14    15    16
     5     6     7     8    17    18    19    20
     9    10    11    12    21    22    23    24

结果与 3.2 节理论推导一致，尺寸为 $\times 8$ 。

模态 3 展开

>> ten2mat(ten, [4, 3, 2], 3)  % 沿模态 3 展开
ans =
     1     2     3     4     5     6     7     8     9    10    11    12
    13    14    15    16    17    18    19    20    21    22    23    24

结果符合模态 3 展开的维度要求（ $\times 12$ ）。

5. 矩阵折叠成高阶张量

矩阵折叠（matrix folding）是张量展开的逆操作，其核心是将展开后的矩阵按指定维度与模态恢复为原始高阶张量。由于折叠过程需严格匹配展开时的维度重组逻辑，其操作复杂度高于张量展开。本节提供 MATLAB 环境下通用的矩阵折叠函数 mat2ten，并通过实例验证其有效性。

5.1 MATLAB 矩阵折叠函数定义

以下 mat2ten 函数可将矩阵按指定的原始张量维度与展开模态，折叠为对应的高阶张量。函数输入包含待折叠矩阵、原始张量各维度尺寸及展开模态，输出为折叠后的高阶张量。

function ten = mat2ten(mat, dim, k)
    % 功能：将矩阵按指定维度与模态折叠为高阶张量（张量展开的逆操作）
    % 输入参数：
    %   mat - 待折叠的矩阵（由张量沿模态 k 展开得到）
    %   dim - 原始张量的维度尺寸向量，格式为 dim = (n1, n2, ..., nd)，其中 d 为张量阶数
    %   k   - 矩阵对应的展开模态，取值范围为 1, 2, ..., d
    % 输出参数：
    %   ten - 折叠后的高阶张量，维度与原始张量一致（n1×n2×...×nd）
    
    % 步骤 1：构造中间维度向量 dim0
    % 逻辑：将原始维度中除模态 k 外的其余维度置于前，模态 k 对应的维度置于最后
    dim0 = [dim(1:k-1), dim(k+1:length(dim)), dim(k)];
    
    % 步骤 2：矩阵转置→维度重塑→维度重排，完成折叠
    % 1. mat'：对待折叠矩阵进行转置，匹配后续维度重塑的元素顺序；
    % 2. reshape(..., dim0)：将转置后的矩阵重塑为中间张量，维度为 dim0；
    % 3. permute(..., [1:k-1, length(dim), k:length(dim)-1])：对中间张量进行维度重排，恢复原始张量的维度顺序
    ten = permute(reshape(mat', dim0), [1:k-1, length(dim), k:length(dim)-1]);
end

5.2 函数有效性验证

为验证 mat2ten 函数的正确性，采用“展开-折叠”循环测试：先将任意高阶张量沿各模态展开为矩阵，再用 mat2ten 将矩阵折叠回张量，通过计算折叠后张量与原始张量的元素绝对误差和，验证两者是否完全一致（误差和为 0 则表示完全匹配）。

5.2.1 测试环境设定

原始张量：5 阶随机张量，维度为 10×9×8×7×6（元素由 rand 函数生成，取值范围 [0,1]）；
验证逻辑：对原始张量沿模态 1 至模态 5 分别执行“展开→折叠”操作，计算每次循环后张量与原始张量的绝对误差总和。

5.2.2 测试代码与结果

% 1. 构造原始 5 阶随机张量
dim = [10, 9, 8, 7, 6];  % 原始张量维度
ten = rand(dim);          % 生成随机张量（元素取值 [0,1]）

% 2. 沿模态 1 验证“展开-折叠”一致性
x1 = abs(mat2ten(ten2mat(ten, dim, 1), dim, 1) - ten);  % 计算绝对误差
sum(x1(:))                                               % 输出误差总和

% 3. 沿模态 2 验证“展开-折叠”一致性
x2 = abs(mat2ten(ten2mat(ten, dim, 2), dim, 2) - ten);
sum(x2(:))

% 4. 沿模态 3 验证“展开-折叠”一致性
x3 = abs(mat2ten(ten2mat(ten, dim, 3), dim, 3) - ten);
sum(x3(:))

% 5. 沿模态 4 验证“展开-折叠”一致性
x4 = abs(mat2ten(ten2mat(ten, dim, 4), dim, 4) - ten);
sum(x4(:))

% 6. 沿模态 5 验证“展开-折叠”一致性
x5 = abs(mat2ten(ten2mat(ten, dim, 5), dim, 5) - ten);
sum(x5(:))

测试结果

ans =
     0
ans =
     0
ans =
     0
ans =
     0
ans =
     0

5.2.3 结果分析

沿所有模态的“展开-折叠”循环后，误差总和均为 0，表明：

mat2ten 函数可准确恢复原始张量的维度结构与元素信息；
函数逻辑与前文定义的 ten2mat（张量展开函数）完全逆向，满足“展开→折叠”的一致性要求；
该函数适用于任意阶数的张量折叠（本例为 5 阶，可推广至更高阶张量）。

Python 环境下的张量展开实现

在 Python 中，可基于 numpy 库的 transpose（维度重排）和 reshape（矩阵重塑）函数设计通用张量展开函数。该函数同样支持任意阶数张量，输入参数与 MATLAB 版本一致，仅需注意 Python 中维度索引从 0 开始（而非 1）。

1 函数定义

import numpy as np

def ten2mat(ten, k):
    """
    将任意阶数张量沿指定模态展开为矩阵
    
    参数：
        ten (numpy.ndarray): 待展开张量，维度为 n1×n2×…×nd
        k (int): 指定的展开模态（Python 索引，0 ≤ k < 张量阶数）
    
    返回：
        numpy.ndarray: 展开后的矩阵，行数为 ten.shape[k]，列数自动计算
    """
    # 步骤1：生成维度重排顺序：将模态 k 置于首位，其余维度按原顺序排列
    perm_order = (k,) + tuple(set(range(ten.ndim)) - {k})
    # 步骤2：对张量进行维度重排
    permuted_ten = np.transpose(ten, perm_order)
    # 步骤3：将重排后的张量重塑为矩阵，行数为 ten.shape[k]，列数自动计算
    mat = permuted_ten.reshape(ten.shape[k], -1)
    return mat

2 函数调用示例

同样以尺寸为 $\times 3 \times 2$ 的张量（元素为 1 至 24 的连续整数）为例，验证各模态展开结果：

步骤 1：构造测试张量

>>> import numpy as np
>>> ten = np.arange(1, 25).reshape(4, 3, 2)  # 生成 4×3×2 的张量
>>> ten  # 查看张量结构（numpy 默认按最后一个维度优先显示）
array([[[ 1, 13],
        [ 5, 17],
        [ 9, 21]],

       [[ 2, 14],
        [ 6, 18],
        [10, 22]],

       [[ 3, 15],
        [ 7, 19],
        [11, 23]],

       [[ 4, 16],
        [ 8, 20],
        [12, 24]]])

步骤 2：模态 1 展开（对应 Python 索引 0）

>>> ten2mat(ten, 0)  # 沿模态 1 展开（Python 索引 0）
array([[ 1,  5,  9, 13, 17, 21],
       [ 2,  6, 10, 14, 18, 22],
       [ 3,  7, 11, 15, 19, 23],
       [ 4,  8, 12, 16, 20, 24]])
```结果与理论推导一致，矩阵尺寸为 $4 \times 6$，符合 $\mathbb{R}^{n_1 \times (n_2 n_3)}$ 的维度要求。

#### 步骤 3：模态 2 展开（对应 Python 索引 1）
```python
>>> ten2mat(ten, 1)  # 沿模态 2 展开（Python 索引 1）
array([[ 1,  2,  3,  4, 13, 14, 15, 16],
       [ 5,  6,  7,  8, 17, 18, 19, 20],
       [ 9, 10, 11, 12, 21, 22, 23, 24]])

结果与理论推导一致，矩阵尺寸为 $\times 8$ ，符合 $\mathbb{R}^{n_2 \times (n_1 n_3)}$ 的维度要求。

步骤 4：模态 3 展开（对应 Python 索引 2）

>>> ten2mat(ten, 2)  # 沿模态 3 展开（Python 索引 2）
array([[ 1,  2,  3,  4,  5,  6,  7,  8,  9, 10, 11, 12],
       [13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24]])

结果符合模态 3 展开的维度要求（ $\times 12$ ），与 $\mathbb{R}^{n_3 \times (n_1 n_2)}$ 一致。

扩展

张量展开的本质：将高阶张量的某一维度作为展开矩阵的行，剩余所有维度按顺序重组为列，本质是“多维度结构向二维矩阵的投影”，目的是将复杂的张量运算转化为成熟的矩阵运算（如矩阵乘法、奇异值分解等）。
模态的关键作用：不同模态对应张量的不同维度，展开模态决定了矩阵化后行维度的物理意义（如在图像张量中，模态 1 可能对应“高度”、模态 2 对应“宽度”、模态 3 对应“通道”）。
实现的共性逻辑：无论是 MATLAB 还是 Python，张量展开的核心步骤均为“维度重排（将目标模态置于首位）→ 矩阵重塑（将剩余维度合并为列）”，该逻辑可推广至任意阶数的张量。

参考文献

张量展开是张量分解（如 PARAFAC 分解、Tucker 分解）、张量回归等领域的基础操作，若需深入学习张量计算的理论与应用，可参考以下经典文献：

[1] Kolda, T. G., & Bader, B. W. (2009). Tensor decompositions and applications. SIAM Review, 51(3), 455-500.（张量分解与应用的奠基性综述，系统阐述了张量展开的数学定义与性质）
[2] Cichocki, A., et al. (2015). Tensor decompositions for signal processing applications: From two-way to multiway component analysis. IEEE Signal Processing Magazine, 32(2), 145-163.（面向信号处理的张量分解应用，包含大量张量展开的工程实例）