An ADC and DAC Least Significant Bit (LSB) | ADC / DAC 中的 LSB

原创已于 2024-11-19 23:26:57 修改 · 1.6k 阅读

24 ·

CC 4.0 BY-SA版权

文章标签：

#ADC / DAC LSB

于 2024-11-17 00:38:20 首次发布

electronic engineering 专栏收录该内容

71 篇文章

订阅专栏

注：机翻，未校。

An ADC and DAC Least Significant Bit (LSB)

ADC 和 DAC 最低有效位（LSB）

by Adrian S. Nastase

Articles on Internet and books show how to calculate the Least Significant Bit (LSB), but they take into consideration either the voltage reference (Vref) or the full scale (FS) of the ADC or DAC. Many times this leads to confusion, as a few messages I received from my readers show. Therefore, this article shows both ways of defining the LSB, so that people will have a clear understanding how to treat an ADC’s (Analog-to-Digital-Converter) or DAC’s (Digital-to-Analog-Converter) LSB.

互联网上的文章和书籍介绍了如何计算最低有效位（LSB），但它们考虑了 ADC 或 DAC 的电压基准（Vref）或满量程（FS）。很多时候这会导致混乱，正如我从读者那里收到的一些信息所显示的那样。因此，本文展示了定义 LSB 的两种方法，以便人们清楚地了解如何处理 ADC （模数转换器）或 DAC （数模转换器） LSB。

What is an LSB? The LSB is the smallest level that an ADC can convert, or is the smallest increment a DAC outputs. Both converters are used at the boundaries between the analog and digital realms, making it possible for the analog circuits to talk to the digital ones and backwards.

什么是 LSB？LSB 是 ADC 可以转换的最小电平，或者是 DAC 输出的最小增量。这两个转换器都用于模拟和数字领域之间的边界，使模拟电路可以与数字电路进行反向通信。

To define an LSB, let’s not look, for the moment, at articles or text books. One of the recommendations I make is this: “When in doubt, read the manufacturer’s data sheet.” So, let us look at an ADC data sheet. The manufacturer writes in the data sheet all the information one needs about that particular component. Sure, nothing is perfect in this world, some info we need might not be there, but in the case of the LSB, I still have yet to see an ADC or DAC data sheet without the LSB definition in some form or another.

要定义 LSB，我们暂时不要看文章或教科书。我提出的建议之一是：“如有疑问，请阅读制造商的数据手册。那么，让我们看看 ADC 数据手册。制造商在数据表中写下需要的有关该特定组件的所有信息。当然，这个世界上没有什么是完美的，我们需要的一些信息可能不存在，但就 LSB 而言，我仍然没有看到没有某种形式的 LSB 定义的 ADC 或 DAC 数据表。

The ADC needs a voltage reference to convert an analog signal into a digital word. Depending on the number of bits it has, the ADC divides the voltage reference in small levels called counts. For example, if this is an 8-bit ADC, the counts will look like those in Figure 1. In an 8-bit ADC there are 28 = 256 counts.

ADC 需要一个电压基准来将模拟信号转换为数字字。根据其位数，ADC 将电压基准分频为称为计数的小电平。例如，如果这是一个 8 位 ADC，则计数将如图 1 所示。在 8 位 ADC 中，有 28 = 256 个计数。

an-8-bit-adc-scale

Figure 1* 图 1

One count is 1 LSB, and is defined as follows:

一个计数为 1 LSB，定义如下：

$\large {LSB}=\frac{Vref}{\mathop{2}^N}$ (1)

where N is the ADC’s or DAC’s number of bits.

其中 N 是 ADC 或 DAC 的位数。

For ADCs that have a differential voltage reference, the LSB is

对于具有差分电压基准的 ADC，LSB 为

$\large {LSB}=\frac{Vref(+)-Vref(-)}{\mathop{2}^N}$ (2)

where Vref(+) and Vref(-) are the non-inverting and the inverting inputs of the differential voltage reference respectively.

其中 Vref（+）和 Vref（-）分别是差分电压基准的同相和反相输入。

The ADC outputs a digital word that shows how many counts are in its input voltage level. As the ADC counts the input level, it never reaches the voltage reference. Its full scale (FS) is calculated with the following formula:

ADC 输出一个数字字，显示其输入电压电平中有多少计数。当 ADC 对输入电平进行计数时，它永远不会达到基准电压源。其满量程（FS）使用以下公式计算：

$\large FS=Vref-1\cdot LSB$ (3)

After replacing the LSB in equation (3), the ADC full-scale results as in equation (4).

替换公式（3）中的 LSB 后，ADC 满量程结果如公式（4）所示。

$\large FS=Vref\cdot \frac{\mathop{2}^{N}-1}{\mathop{2}^{N}}$ (4)

Figure 2 shows the ADC counts and the corresponding hex code.

图 2 显示了 ADC 计数和相应的十六进制代码。

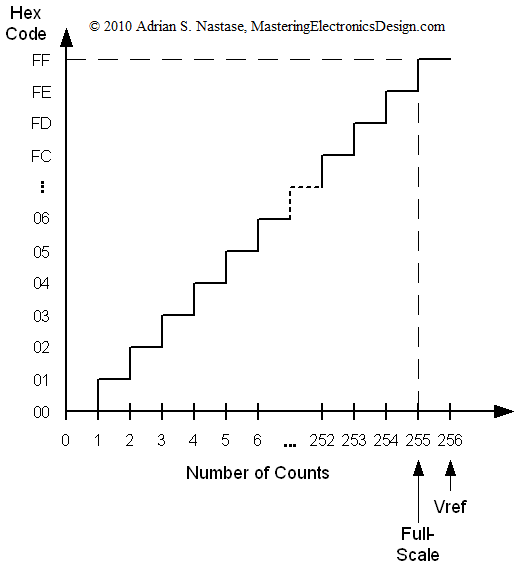
8-bit-adc-lsb

Figure 2 图 2

In our 8-bit ADC example, if the voltage reference is Vref = 5V, then the LSB and FS are:

在我们的 8 位 ADC 示例中，如果电压基准为 Vref = 5V，则 LSB 和 FS 为：

$\large LSB=\frac{Verf}{\mathop{2}^{N}}=\frac{5V}{\mathop{2}^{8}}=19.531\text{ }mV$

and

$\large FS=Vref-1\cdot LSB=4.98047\text{ }V$ (5)

As you can see, and ADC can never reach its Vref but, as the number of bits is higher, it gets very close to its reference voltage. The same can be said about a DAC.

如您所见，ADC 永远无法达到其 Vref ，但是，随着位数的增加，它非常接近其基准电压。 DAC 也是如此。

Moreover, from equation (1), we can write the mathematical relation between Vref and LSB as follows:

此外，从公式（1）中，我们可以写出 Vref 和 LSB 之间的数学关系如下：

$\large Vref={{2}^{N}}\cdot LSB$ (6)

If we replace Vref in equation (3), and after calculations, we can write the definition of the LSB as a function of the ADC’s full-scale, as in equation (7).

如果我们替换公式（3）中的 Vref，经过计算，我们可以将 LSB 的定义写成 ADC 满量程的函数，如公式（7）所示。

$\large LSB=\frac{FS}{{{2}^{N}}-1}$ (7)

This is the trouble, as the LSB has two definitions, equations (1) and (7). Both of them are valid, and some authors are ambiguous or confused about them. I have seen articles in which Vref is considered the component full-scale, which is the premise that generates subsequent wrong definitions.
这是问题所在，因为 LSB 有两个定义，即方程（1）和方程（7）。这两者都是有效的，但一些作者对此存在模糊或困惑。我见过一些文章，其中 Vref 被视为组件的满量程，这一前提导致后续错误定义的产生。

Therefore, all one needs to remember about the LSB is its definition, as follows:

因此，关于 LSB，只需记住它的定义，如下所示：

$\large LSB=\frac{Vref}{{{2}^{N}}}$

$\large LSB=\frac{FS}{{{2}^{N}}-1}$

where $\large FS=Vref-1\cdot LSB$

(8)

>>> <<< >>><<<

Here are some data sheet examples:

以下是一些数据表示例：

AD7823, 8-Bit ADC, manufacturer Analog Devices

If Vref = 2.5 V then
1LSB = 9.766 mV,
FS = Vref – 1 LSB = 2.490234 V
If Vin = FS = 2.490234 V, then ADC Hex Code = FF, and
If Vin = 0 V, then ADC Hex Code = 00.

If Vref = 5 V then
1LSB = 19.531 mV,
FS = Vref – 1 LSB = 4.980469 V
If Vin = FS = 4.980469 V, then ADC Hex Code = FF, and
If Vin = 0 V, then ADC Hex Code = 00.

AD7685, 16-Bit ADC, manufacturer Analog Devices

If Vref = 2.5 V then
1LSB = 38.1 uV,
FS = Vref – 1 LSB = 2.499962 V
If Vin = FS = 2.499962 V, then ADC Hex Code = FFFF, and
If Vin = 0 V, then ADC Hex Code = 0000.

If Vref = 5 V then
1LSB = 76.3 uV,
FS = Vref – 1 LSB = 4.999924 V
If Vin = FS = 4.999924 V, then ADC Hex Code = FFFF, and
If Vin = 0 V, then ADC Hex Code = 0000.

DAC8830, 16-Bit DAC, manufacturer Texas Instruments

If Vref = 2.5 V then
1LSB = 38.1 uV,
FS = Vref – 1 LSB = 2.499962 V
If DAC Hex Code = FFFF, then Vout = FS = 2.499962 V, and
If DAC Hex Code = 0000, then Vout = 0 V.

If Vref = 5 V then
1LSB = 76.3 uV,
FS = Vref – 1 LSB = 4.999924 V
If DAC Hex Code = FFFF, then Vout = FS = 4.999924 V, and
If DAC Hex Code = 0000, then Vout = 0 V.

ADC 或 DAC 中的 LSB（该文示例引自上文）

CodeForCoffee 于 2020-12-26 16:20:41 发布

概述

有朋友问电子测量中分辨率的问题

分辨率 (Resolution) 与 LSB 是本质上是相同的，是描述一件事情的两个角度。

一般的数字电路教材中都有

LSB 是 Least Sigificant Bit 的缩写，即最低有效位

计算 ADC 或 DAC 的 LSB 时，经常会用到以下两者之一：

Vref ( the voltage reference ) 参考电压
FS ( the full scale ) 满量程

对于 ADC 而言，LSB 是 ADC 能识别（或转换出）的最小刻度

对于 DAC 而言，LSB 是 DAC 的最小输出

以 ADC 为例

一颗 8 位的 ADC，其具有 2 的 8 次方，即 256 个刻度

如下图所示，Vref 与 FS 都标注得很清楚了

LSB

一个刻度（count）就是 1 个 $L SB$

$L SB$ 可以这样计算：

$\displaystyle {LSB}=\frac{Vref}{\mathop{2}^N}$

上式中 $N$ 表示位数

FS

$FS$ 与 $V re f$ 之间相差 1 个 $L SB ，即$

$\displaystyle {FS}={Vref}-1{ }\!\!\cdot\!\!{ LSB}$

值得注意的是，ADC 永远无法达到 Vref，其最多只能达到 FS，距离 Vref 还有 1 个 LSB。

当然也有一些书中对于 Vref 和 FS 不加明确的区分。

对于 LSB 的理解（位的 LSB、模数转换的 LSB）

机载软件与适航已于 2022-06-29 22:36:34 修改

之前对于 LSB 的理解：

最高有效位（MSB）指二进制中最高值的比特。在 16 比特的数字音频中，其第 1 个比特便对 16bit 的字的数值有最大的影响。例如，在十进制的 15389 这一数字中，相当于万数那 1 行（1）的数字便对数值的影响最大。比较与之相反的 “最低有效位”（LSB）。

汇编中，比如，8 位 2 进制数 10000001，其中第一个 1 是 MSB, 第二个 1 是 LSB。在计算机计算的时候用于判断。比如，如果是整数那么小数点（实际上是没有小数点的，但就把那一位和下一位之间看作有）在 LSB 后面，如果是小数小数点在 MSB 后面，其中 MSB 在有符号数中又是符号位。

LSB (Least Significant Bit) 是 “最低有效位”。MSB (Most Significant Bit) 是 “最高有效位”。

如一个地址：

1（MSB）100 0011（LSB）

在网络通信方面，大家说的更多的是：“Big-Endian” 和 “Small-Endian” 的问题。

指的都是对于多字节的数据类型（比如 4 字节的 32 位整数），其多个字节的顺序问题，是最高字节在前（Big-Endian）还是最低字节在前（Small-Endian）。

比如对于 0x12345678 这个数，那么按照 Small-Endian 的方式，它在网络上传输（或者在内存里存储）的 4 个字节依次是：12 34 56 78（右为低地址）（地址的增长顺序与值的增长顺序相同，12 为千万位），而 Big-Endian 的顺序正相反，是：78 56 34 12（右为低地址）（地址的增长顺序与值的增长顺序相反）。

MSB 和 LSB 虽然跟这个事情看起来有点相似，但不是一回事。通常，一个芯片的管脚中，对于一个多比特的信号，比如 32 根的地址线，从低开始按 0 到 31 编个号。MSB 就是 31，LSB 就是 0。那么如果标记为：ADDR [31:0] 就是 MSB first 的方式，如果标记为 ADDR [0:31] 就是 LSB first 的方式。

MSB LSB：起始地址为最高位，最后地址为最低位。

LSB MSB：起始地址为最低位，最后地址为最高位。

比如 AD 中，8 位，最低有效位指 D0

A/D 和 D/A 中的 LSB

A/D 是模拟量到数字量的转换，依靠的是模数转换器 (Analog to Digital Converter)，简称 ADC。

D/A 是数字量到模拟量的转换，依靠的是数模转换器 (Digital to Analog Converter)，简称 DAC。它们的道理是完全一样的，只是转换方向不同，因此我们讲解过程主要以 A/D 为例来讲解。

很多同学学到 A/D 这部分的时候，感觉是个难点，概念搞不清楚，掌握不好。我个人认为主要原因不在于技术问题，而是不太会感悟生活。我们生活中有很多很多 A/D 的例子，只是没有在单片机领域里应用而已，下面我带着大家一起感悟一下 A/D 的概念。

什么是模拟量？就是指变量在一定范围内连续变化的量，也就是在一定范围内可以取任意值。

比如米尺，从 0 到 1 米之间，可以是任意值。什么是任意值，也就是可以是 1cm，也可以是 1.001cm，当然也可以 10.000„„后边有无限个小数。总之，任何两个数字之间都有无限个中间值，所以称之为连续变化的量，也就是模拟量。

而我们用的米尺上被我们人为的做上了刻度符号，每两个刻度之间的间隔是 1mm，这个刻度实际上就是我们对模拟量的数字化，由于有一定的间隔，不是连续的，所以在专业领域里我们称之为离散的。

ADC 就是起到把连续的信号用离散的数字表达出来的作用。那么我们就可以使用米尺这个 “ADC” 来测量连续的长度或者高度这些模拟量。如图 17-1 一个简单的米尺刻度示意图。

图 17-1 米尺刻度示意图

我们往杯子里倒水，水位会随着倒入的水量的多少而变化。现在就用这个米尺来测量我们杯子里的水位的高度。水位变化是连续的，而我们只能通过尺子上的刻度来读取水位的高度，获取我们想得到的水位的数字量信息。这个过程，就可以简单理解为我们电路中的 ADC 采样。

我们在选取和使用 A/D 的时候，依靠什么指标来判断很重要。由于 AD 的种类很多，分为积分型、逐次逼近型、并行 / 串行比较型、Σ-Δ 型等多种类型。同时指标也比较多，并且有的指标还有轻微差别，在这里我是以同学们便于理解的方法去讲解，如果和某一确定类型 A/D 概念和原理有差别，也不会影响实际应用。

ADC 的位数

一个 n 位的 ADC 表示这个 ADC 共有 2 的 n 次方个刻度。8 位的 ADC，输出的是从 0～255 一共 256 个数字量，也就是 2 的 8 次方个数据刻度。

基准源

基准源，也叫基准电压，是 ADC 的一个重要指标，要想把输入 ADC 的信号测量准确，那么基准源首先要准，基准源的偏差会直接导致转换结果的偏差。

比如一根米尺，总长度本应该是 1 米，假定这根米尺被火烤了一下，实际变成了 1.2 米，再用这根米尺测物体长度的话自然就有了较大的偏差。假如我们的基准源应该是 5.10V，但是实际上提供的却是 4.5V，这样误把 4.5V 当成了 5.10V 来处理的话，偏差也会比较大。

分辨率

分辨率是数字量变化一个最小刻度时，模拟信号的变化量，定义为满刻度量程与 $2^n - 1$ 的比值。假定 5.10V 的电压系统，使用 8 位的 ADC 进行测量，那么相当于 0～255 一共 256 个刻度把 5.10V 平均分成了 255 份，那么分辨率就是 $\frac{5.10}{255} = 0.02V$ 。

INL（积分非线性度）和 DNL（差分非线性度）

初学者最容易混淆的两个概念就是 “分辨率” 和 “精度”，认为分辨率越高，则精度越高，而实际上，两者之间是没有必然联系的。分辨率是用来描述刻度划分的，而精度是用来描述准确程度的。同样一根米尺，刻度数相同，分辨率就相当，但是精度却可以相差很大，如图 17-2 所示。

图 17-2 米尺精度对比

图 17-2 表示的精度一目了然，不需多说。和 ADC 精度关系重大的两个指标是 INL (Integral NonLiner) 和 DNL (Differencial NonLiner)。

INL 指的是 ADC 器件在所有的数值上对应的模拟值，和真实值之间误差最大的那一个点的误差值，是 ADC 最重要的一个精度指标，单位是 LSB。

LSB（Least Significant Bit）是最低有效位的意思，那么它实际上对应的就是 ADC 的分辨率。一个基准为 5.10V 的 8 位 ADC，它的分辨率就是 0.02V，用它去测量一个电压信号，得到的结果是 100，就表示它测到的电压值是 100*0.02V=2V，假定它的 INL 是 1LSB，就表示这个电压信号真实的准确值是在 1.98V～2.02V 之间的，按理想情况对应得到的数字应该是 99～101，测量误差是一个最低有效位，即 1LSB。

DNL 表示的是 ADC 相邻两个刻度之间最大的差异，单位也是 LSB。一把分辨率是 1 毫米的尺子，相邻的刻度之间并不都刚好是 1 毫米，而总是会存在或大或小的误差。同理，一个 ADC 的两个刻度线之间也不总是准确的等于分辨率，也是存在误差，这个误差就是 DNL。

一个基准为 5.10V 的 8 位 ADC，假定它的 DNL 是 0.5LSB，那么当它的转换结果从 100 增加到 101 时，理想情况下实际电压应该增加 0.02V，但 DNL 为 0.5LSB 的情况下实际电压的增加值是在 0.01～0.03V 之间。

值得一提的是 DNL 并非一定小于 1LSB，很多时候它会等于或大于 1LSB，这就相当于是一定程度上的刻度紊乱，当实际电压保持不变时，ADC 得出的结果可能会在几个数值之间跳动，很大程度上就是由于这个原因（但并不完全是，因为还有无时无处不在的干扰的影响）。

转换速率

转换速率，是指 ADC 每秒能进行采样转换的最大次数，单位是 sps（或 s/s、sa/s，即 samples per second），它与 ADC 完成一次从模拟到数字的转换所需要的时间互为倒数关系。ADC 的种类比较多，其中积分型的 ADC 转换时间是毫秒级的，属于低速 ADC；逐次逼近型 ADC 转换时间是微妙级的，属于中速 ADC；并行 / 串行的 ADC 的转换时间可达到纳秒级，属于高速 ADC。

ADC 的这几个主要指标大家先熟悉一下，对于其它的，作为一个入门级别的选手来说，先不着急深入理解。以后使用过程中遇到了，再查找相关资料深入学习，当前重点是在头脑中建立一个 ADC 的基本概念。

分辨率和精度的概念

很多 A/D 转换器和仪器厂商常拿分辩率来忽悠人，很多人的确上套，即使专业人士也常常逃不过。其实这两者的区别很大，但有联系。

1, 精度是接近真实值的程度，即绝对误差或相对误差的大小。精度做到 0.01% 极其难

2, 分辩率是量化刻度的细度大小，分辩率做到 0.00001% 不很难 (如 24 位 A/D,0.0000056%)

3, 概念理解：

例 1: 一把 1 米的软尺，有 1000 个刻度，分辩率 1 毫米 (分辩率 0.1%), 用标准尺量下绝对误差 + 5 毫米，精度 + 0.5%。如果能把尺拉长 20 毫米，此时绝对误差 + 25 毫米，精度降为 2.5%, 可是尺还是 1000 个刻度，其分辨率还是 1 毫米 (0.1%).

例 2: 两杆称来称真重 1 克的物体，一杆的结果为 1.03 克，另一杆的结果为 0.8333333333333333333333333 克，哪个准呢？

4, 关系

分辩率高是精度高的必要条件，不是充分条件；分辩率高不等于精度高，认定精度才是王道。

“精度” 是用来描述物理量的准确程度，其反应的是测量值与真实值之间的误差，而 “分辨率” 是用来描述刻度划分的，其反应的是数值读取过程中所能读取的最小变化值。简比喻：一把常见的量程为 10 厘米的刻度尺，上面有 100 个刻度，最小能读出 1 毫米的有效值。那么我们就说这把尺子的分辨率是 1 毫米，他只能 1、2、3、4……100 这样读值；而它的实际精度就不得而知了，因为用这把尺读出来的 2 毫米，我们并不知道他与真实绝对的 2 毫米之间的误差值。而当我们用火来烤一下它，并且把它拉长一段，然后再考察一下它。我们不难发现，它还有 100 个刻度，因而它的 “分辨率” 还是 1 毫米，跟原来一样！然而，它的精度显然已经改变了。

对于编码器来说，“分辨率” 除了与刻线数有关外，还会因电气信号方面的影响而改变，它是可调的，可控的，它可以随着对信号的细分而改变，细分倍数越高，分辨率越小，但是细分倍数越高，引入加大的误差就越大。而精度，更多的偏向于机械方面，一个产品生产出来后，他的精度基本已经固定 (有些高精度的产品可以对信号进行补偿等来提高精度)，这个数值是通过检测出来的，它与产品的做工，材料等综合性能息息相关，我们难以通过计算来得出一个具体的数值作为精度的依据，大多只能在使用的过程当中判断出精度的好坏来。

例如，对于 13bit 的，其码盘上的绝对位置数为：8192，则：计算出的分辨率为 158 角秒，也就是说，在读取数值的时候，要求数值间的跳动是 158 角秒，如果要读取的第一个数值是 0，则第二个读取的数值要大于 158，若要小于 158，则我们需要选取更小的分辨率。当要读取 158 这个数值的时候，由于误差的存在，并不可能得到绝对的 158 秒，编码器所读取出来的 158 秒与绝对真实 158 秒之间的误差，就取决于精度了。所以说，精度，是在分辨率的基础上来谈的。

而并非越细分得到小的分辨率就越好，因为细分会引入误差和扩大误差，过度的细分将无法保证精度！需要多少倍的细分，能做到多少倍的细分，前提必须是在保证精度的基础上进行的，因为精度在使用前的不可见性而高倍细分是不负责任的。码盘质量越高，刻线越好，信号质量信号越好，细分后产生的误差就越小，这受到一台编码器综合性能的影响，这也就是为什么会在相同的参数下，会有不同品牌，不同价位编码器的一个原因。

例如，我们要读取的数值为 1、2、4、7、8，我至少要选择 1 个单位的分辨率，选择 2 个单位的分辨率是显然不行的，因为我们读出了 1 这个数值，则 2 是读不出来的，在选择 1 个单位分辨率的基础上，我们读出来的 1 与真实绝对的 1 的误差就是精度。机床上的数控系统对于直光栅是有分辨率的设定的，需要读取的数值间隔小于分辨率，机床就有可能会抖动或出错等。

对于绝对式带增量信号编码器，能够精确的保持串行传输的绝对位置值与增量值同步，绝对值确切的对应一个增量信号，位置值一定在一个增量信号的正弦周期之内。如 13 位绝对式，带 512 线的增量信号，绝对位置间隔 158 秒，若要读取两个码盘位置中间的一个位置是不合适的，但是，我们可以通过对其所带的 1Vpp 增量信号进行细分，如细分 100 倍，则相当于在两个绝对位置之间又引入了几个细分后的位置，我们可以在绝对位置值的基础上，通过计算细分后的增量脉冲数而读取两个绝对位置之间的一个位置值，如：512 线细分 100 倍，绝对位置 1 数值是 0，绝对位置 2 数值是 158，则读取这两个位置间的位置可以在位置 1：数值 0 的基础上多出一个脉冲则是 25，两个则是 25x2=50…… 但是，带增量信号的绝对式编码器本身是不带细分的，这就要求用户能自行的对增量信号进行细分处理。