四元数 | 一个方程如何改变了数学史

数学史上著名涂鸦与谷歌数学涂鸦故事

原创已于 2025-08-10 14:32:31 修改 · 1.5k 阅读

12 ·

CC 4.0 BY-SA版权

文章标签：

#数学

于 2024-10-20 09:41:23 首次发布

mathematics 专栏收录该内容

191 篇文章

订阅专栏

注：本文为 “四元数” 相关合辑。
英文引文，机翻未校。
中文引文，略作重排。
如有内容异常，请看原文。

数学史上最著名的涂鸦

原创 Arianrhod 原理

1843 年 10 月 16 日，爱尔兰数学家 哈密顿（William Rowan Hamilton，1805～1865）在都柏林皇家运河边散步时，突然迎来了一个顿悟时刻！

都柏林皇家运河上的布鲁姆桥上的一块牌匾，纪念了哈密顿的灵光一闪。（图 / William Murphy / Flickr, CC BY）

在这里插入图片描述

Photo of a plaque with inscription ‘Here as he walked by on the 16th of October 1843 Sir William Rowan Hamilton in a flash of genius discovered the fundamental formula for quaternion multiplication $i^2 = j^2 = k^2 = ijk = -1$ & cut it on a stone of this bridge.’

A plaque on Dublin’s Broome Bridge commemorate’s Hamilton’s flash of insight. Cone83 / Wikimedia, CC BY-SA

都柏林布鲁姆大桥（Broome Bridge）上的一块牌匾纪念汉密尔顿（Hamilton）的灵光一闪。

他非常兴奋，拿出小刀，当场就把他得到的启示刻在了布鲁姆桥上：

$\Large i^2 = j^2 = k^2 = ijk = -1$

这是数学史上最著名的涂鸦，虽然它看起来 “平平无奇”，但它却改变了数学家表示信息的方式，并使得无数的技术应用得以变得更加简单。那么，这个著名的涂鸦是什么意思呢？

旋转的物体

哈密顿试图解决的数学问题是，如何在 三维空间 中表示不同方向之间的关系。我们对方向并不陌生，它在描述力或速度等物理量时至关重要，但哈密顿感兴趣的是有关 三维旋转 的问题。

数学家已经知道如何用坐标（如 $x 、 y 、 z$ ）来表示物体的位置，但想要知道当这些物体在旋转时坐标发生了什么变化，就需要运用复杂的球几何。哈密顿想要一种更简单的方法。

他的灵感源自于一种表示 二维旋转 的方法，这种方法涉及到复数。复数是由一个实部和一个虚部构成的，虚部是虚数*i* 的倍数，即 “-1 的平方根”。

$\Large i^2=-1$

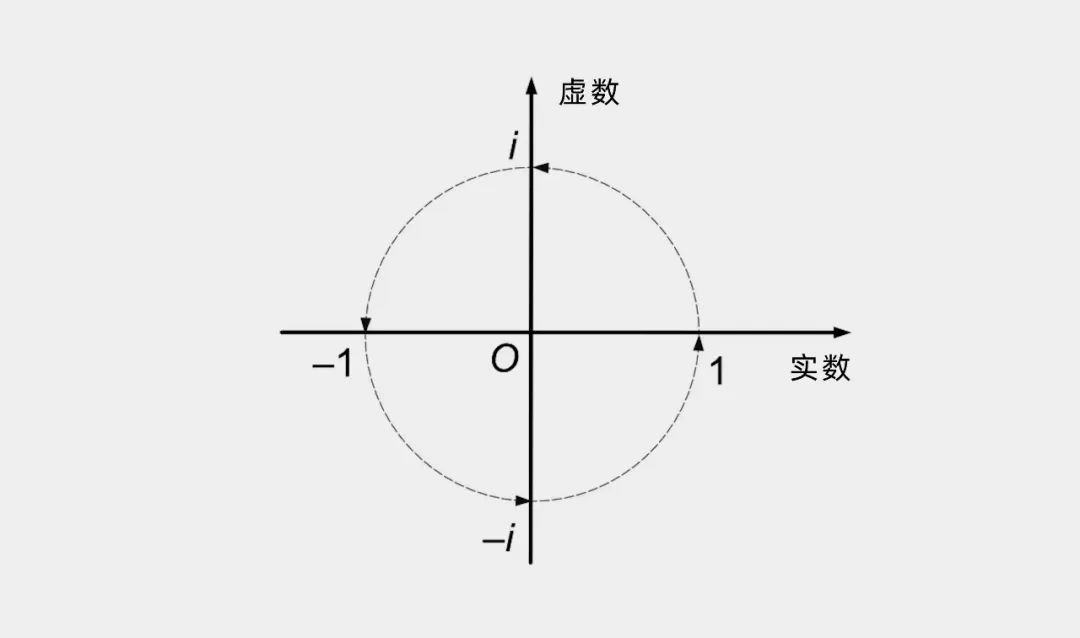
到 19 世纪初，包括 阿尔冈（Jean Argand）和沃伦（John Warren）在内的几位数学家发现，复数可以用平面上的一个点来表示。沃伦还证明，要在这个复平面上将一条直线旋转 90°，在数学上是很容易办到的，因为这是当一个数乘以 i 的结果。

当把一个复数表示为复平面上的一个点时，将这个数字乘以 $i$ ，就相当于将相应的直线逆时针旋转 90°。

复数与几何之间的这种关联给了哈密顿启发，他开始尝试在三维空间中对其进行研究。他想象了一个三维复平面，沿着第二个虚数 j 的方向是第二个虚轴，这个虚轴垂直于另外两个轴。

他花了好几个月的时间才意识到，如果他想把二维旋转中的 “i 乘法” 扩展，那么 他需要具有第三个虚数 *k* 的四维复数。

在这个四维数学空间中， $k$ 轴垂直于其他三个轴。而且 $k^2 = -1$ ，并且根据定义， $k = ij = - ji$ 。结合这两个方程，就能得到

$\Large ijk = -1$

把所有这些都结合在一起，就能得到关键的 $i^2 = j^2 = k^2 = ijk = -1$ 这个启示就像一道闪电，击中了布鲁姆桥上的哈密顿。

四元数和向量

哈密顿把他的四维数称为 “四元数”，并用它们来计算三维空间中的几何旋转。这也是今天人们用来移动机器人，以及定位卫星的旋转方式。但是大多数 “奇妙的用途” 只在仅考虑四元数的虚部时才会出现。这就是哈密顿所说的 “向量”。

四元数（Quaternions），是由爱尔兰数学家哈密顿（William Rowan Hamilton,1805-1865）在 1843 年发明的数学概念，直到 1985 年才由 Shoemake 把四元数引入到计算机图形学中。

一个向量可以同时编码两种信息，最著名的是如力、速度，或相对位置这类空间量的 大小和方向。

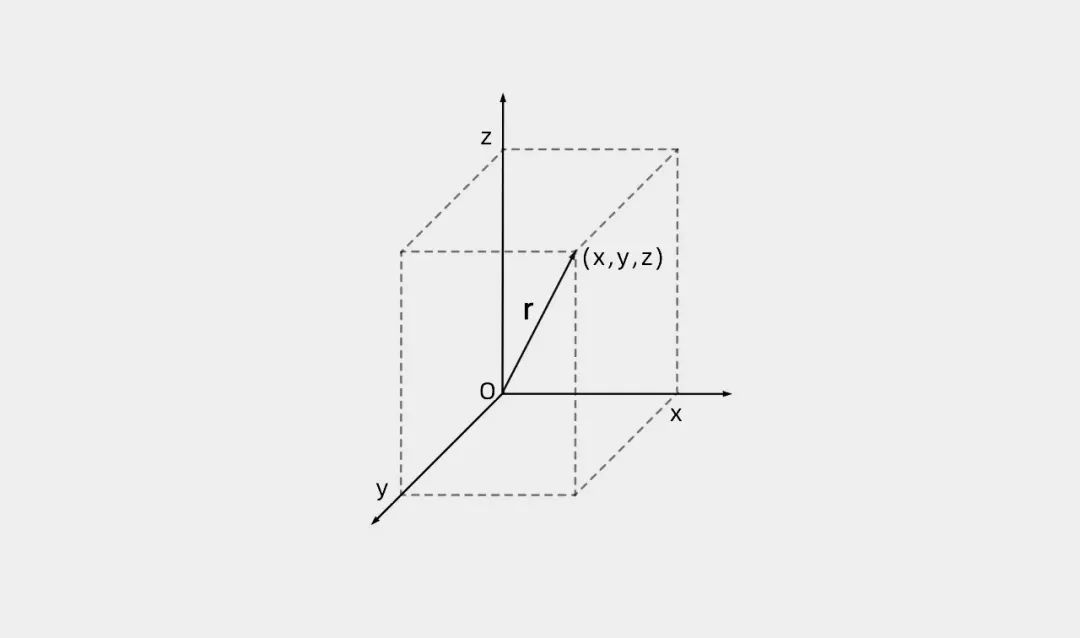
例如，为了表示一个物体相对于 “原点”（数轴上的零点）的位置 $(x, y, z)$ ，哈密顿使用了一个从原点指向物体位置的箭头来表示。这个箭头表示位置向量： $\mathbf{i} + y \mathbf{j} + z \mathbf{k}$ 。这个向量的 “分量” 是数字 $x$ 、 $y$ 、 $z$ ，也就是箭头沿着三个数轴中的每一个延伸的距离。

向量 $r$ 就像从点 O 到坐标 $（ x, y, z ）$ 的箭头。

半个世纪后，英国电报员亥维赛（Oliver Heaviside）帮助开创了现代向量分析，他用实单位向量 $i 、 j 、 k$ 取代了哈密顿的虚单位向量 $i 、 j 、 k$ 。但无论在哪种情况下，向量的分量都保持不变，因此箭头和向量乘法的运算法则也保持不变。

奥利弗・亥维赛（Oliver Heaviside，1850 年 5 月 18 日－1925 年 2 月 3 日），英国自学成才的物理学家。1880年，他研究电报传输上的集肤效应。他将在电磁学上举足轻重的麦克斯韦方程组重新表述，由四元数改为向量，将原来20条方程减到4条微分方程。

亥维赛和他的科学成就
http://home.ustc.edu.cn/~lxsphys/2021-4-8/亥维赛和他的科学成就.pdf

哈密顿定义了两种向量相乘的方法：一个产生的是数字，即所谓的 标量积 或点积；另一个产生的是向量，即所谓的 向量积 或叉积。如今，这些乘法在许多应用中都存在，例如支撑我们所有电子设备的电磁学方程。

一个数学对象

哈密顿不知道的是，其实在三年前，法国数学家 罗德里格（Olinde Rodrigues）就在关于旋转的研究中，提出了这些乘积的一个版本。把罗德里格的乘法称为向量的乘积是后见之明。而哈密顿是那个把这些分开的分量结合成一个单独的向量的人。

本杰明·奥林德·罗德里格斯（Benjamin Olinde Rodrigues，1795 年 10 月 6 日-1851 年 12 月 17 日）法国数学家，以其勒让德多项式公式而闻名。

其他人，从牛顿到罗德里格，都没能发展出一个单一的数学对象来统一地描述位置或力的分量。值得一提的是，还有一个人也有类似的想法，那就是自学成才的德国数学家 ——格拉斯曼（Hermann Grassmann），他独立地发展出了一个不那么直观的向量系统。

赫尔曼·京特·格拉斯曼（Hermann Günther Graßmann，1809年4月15日—1877年9月26日），出生于什切青，是一个德国博学者，在他生活的时代以语言学家身份闻名，今天以数学家身份而著称。他也是一位物理学家，新人道主义者，博学家和出版家。什切青（Szczecin）现属波兰，在历史上，什切青的归属经历了多次变化。

哈密顿还发展了一套简洁的符号来使他的方程更简明优雅。他用希腊字母来表示四元数或向量，但在亥维赛之后，人们通常使用粗体的拉丁字母来表示。哈密顿的这种紧凑的符号改变了数学家在三维空间中表示物理量的方式。比如 麦克斯韦（James Clerk Maxwell）的电磁学方程就是很典型的例子。

$\displaystyle\nabla \times \mathbf{E} = -\frac{\partial \mathbf{B}}{\partial t}$

仅用少数几个符号，就展示了电场向量 (E) 在空间中的传播会如何受磁场向量 (B) 的影响。

如果没有向量符号，这样一个短短的公式将要被写成三个独立的方程（每个代表 B 和 E 的每个分量），每一个都是一堆坐标、乘法和减法。

$\displaystyle\frac{\partial E_{z}}{\partial y} - \frac{\partial E_{y}}{\partial z} = -\frac{\partial B_{x}}{\partial t}$

$-\displaystyle\frac{\partial E_{z}}{\partial x} + \frac{\partial E_{x}}{\partial z} = -\frac{\partial B_{y}}{\partial t}$

$\displaystyle\frac{\partial E_{y}}{\partial x} - \frac{\partial E_{x}}{\partial z} = -\frac{\partial B_{z}}{\partial t}$

上述方程的展开形式。

毅力的力量

之所以选择麦克斯韦的一个方程作为例子，是因为麦克斯韦是第一个认识到这种简洁的向量符号拥有巨大潜力的主流物理学家。但可惜的是，哈密顿并没能活着看到麦克斯韦的支持。

不过，在面对主流的排斥时，哈密顿表现出了惊人的毅力。他希望终有一天，他的发现会被感激，这种愿望并非出自于虚荣心，而是他预见了一些可能的运用前景。

如果他知道向量在今天被如此广泛地使用，而且它们既可以表示数字信息，也可以表示物理信息，他应该会欣喜若狂。并且他会尤为高兴在旋转编程中，四元数仍然是最好的选择。

原文：Robyn Arianrhod（莫纳什大学）

篇外一：关于 $i\, j\, k = -1$ 的讨论

注：机翻，未校。

Quaternions: why does $ijk = - 1$ and $ij = k$ and $- ji = k$

四元数：为什么 $ijk = - 1$ 以及 $ij = k$ 和 $- ji = k$

edited Apr 23, 2023 at 21:10

mau

asked Feb 6, 2013 at 15:54

Jordi Ozir

I do understand that $i$ , $j$ and $k$ are imaginary numbers. so $i^2=j^2=k^2=-1$ . But I could not understand this:

我确实理解 $i$ , $j$ 和 $k$ 是虚数。所以 $i^2=j^2=k^2=-1$ 。但我不能理解这个：

$ij = k$ , $jk = i$ , $ki = j$ , $ji = - k$ , $kj = - i$ , $ik = - j$

Why is this? There seems no explanation why that is true. I would like to understand why that is true instead of just assuming that that is true.

这是为什么？似乎没有解释为什么这是真的。我想理解为什么这是真的，而不仅仅是假设这是真的。

The defining properties relating $i$ , $j$ , and $k$ are $i^2=-1$ , $j^2=-1$ , $k^2=-1$ , $ijk = - 1$ .

定义 $i$ , $j$ , 和 $k$ 的属性是 $i^2=-1$ , $j^2=-1$ , $k^2=-1$ , $ijk = - 1$ .

From these you get for example that $i(ijk)=i^2jk=-i \Rightarrow jk=i$ .

从这些你可以例如得到 $i(ijk)=i^2jk=-i \Rightarrow jk=i$ .

These properties/definitions produce interesting and useful results, so we /axiomatically/ make them true for this structure. There is no deeper reason. We just want to study something that behaves in such a manner.

这些属性/定义产生了有趣和有用的结果，所以我们公理化地使它们对这种结构成立。没有更深层次的原因。我们只是想研究以这种方式表现的东西。

i, j, k are not imaginary numbers. Imaginary numbers arise only when you are talking about the complex plane $C$ , which has a very simple one to one mapping with the 2-D plane $R^2$ . Quaternions arise when you are talking about three dimensions, i.e. looking for solutions to $x^2+1=0$ in $3 - D$ .

$i$ , $j$ , $k$ 不是虚数。虚数只有在你谈论复平面 $C$ 时才会出现，它与 $2 - D$ 平面 $R^2$ 有一个非常简单的一一映射。当你谈论三维时，会出现四元数，即在 $3 - D$ 中寻找 $x^2+1=0$ 的解。

If you want to get a physical picture, consider $i$ as rotating a vector or a line segment in $3 - D$ by $90^\circ$ taking X-axis as the axis of rotation. Similarly, $j$ , $k$ correspond to rotations about Y and Z axes respectively. This is similar to imaginary number $i$ , which corresponds to a right angle rotation in the complex plane. Since in $3 - D$ there are more than one independent axes of rotation possible, 3 to be precise, there are 3 quaternions.

如果你想得到一个物理图像，考虑 $i$ 作为在 $3 - D$ 中旋转一个向量或线段 $90^\circ$ ，以 $X$ 轴为旋转轴。同样， $j$ , $k$ 分别对应于关于Y轴和Z轴的旋转。这与虚数 $i$ 类似，它对应于复平面中的直角旋转。由于在 $3 - D$ 中有多于一个独立的旋转轴可能，确切地说是 3 个，因此有 3 个四元数。

Now, two $90^{\circ}$ rotations about X, Y or Z axis will take the vector $\mathbf{x}$ to its mirror image $\mathbf{(-x)}$ . So, $i^2=j^2=k^2 =-1$ .

现在，绕 $X 、 Y$ 或 $Z$ 轴旋转两次 $90^{\circ}$ ，向量 $\mathbf{x}$ 就会变成它的镜像 $\mathbf{(-x)}$ 。所以, $i^2 = j^2 = k^2 = -1$ 。

A right angle rotation about X axis followed by an equal amount of rotation about Y corresponds to an overall effective rotation of $90^\circ$ about Z axis. So, $ij = k$ . Similarly, you can physically verify the quaternion multiplication laws.

关于X轴的直角旋转，然后是关于Y轴的等量旋转，对应于关于 $Z$ 轴的总体有效旋转 $90^\circ$ 。所以， $ij = k$ 。同样，你可以物理验证四元数乘法法则。

Do not try to think of their multiplication as arithmetic. They are compositions of rotation operations. If this looks too confusing, a little background in group theory will bring you enough mathematical maturity to be comfortable with these.

不要试图将它们的乘法视为算术。它们是旋转操作的组合。如果这看起来太令人困惑，那么一些群论的背景将给你带来足够的数学成熟度，以适应这些。

You can derive the properties of quaternions through clifford algebra and the geometric product of vectors.

你可以通过克利福德代数和向量的几何积来推导出四元数的属性。

The geometric product works like so:

几何积的工作方式如下：

$e_a e_b = \begin{cases} 1, & a = b \\ -e_b e_a, & a \neq b \end{cases}$

where $a, b$ can be $x$ , $y$ , or $z$ as usual. This captures both the work of the cross product and the dot product in one product of basis vectors.

其中 $a, b$ 可以是 $x$ , $y$ , 或 $z$ 如常。这在一个基向量的乘积中同时捕捉了叉积和点积的工作。

You can then identify

然后你就可以识别

$KaTeX parse error: {align*} can be used only in display mode.$

And then the properties of quaternions naturally follow.

然后四元数的属性自然随之而来。

$i^2 = (-e_y e_z)(-e_y e_z) = (e_y e_z)(e_y e_z) = -e_y(e_z e_z)e_y = -e_y e_y = -1$

And similarly for $j^2$ and $k^2$ , as well as the $ijk$ product:

以及 $j^2$ 和 $k^2$ ，以及 $ijk$ 乘积：

$ijk = (-e_y e_z)(-e_z e_x)(-e_x e_y) = -e_y e_z e_z e_x e_x e_y = -e_y(e_z e_z)(e_x e_x)e_y = -e_y e_y = -1$

This allows you to interpret quaternions in a very geometric way: the $i$ , $j$ , $k$ do not represent vectors, but rather oriented planes. It’s just that in 3d each plane has a unique normal vector, so we often abuse this duality.

这允许你以非常几何的方式解释四元数： $i$ , $j$ , $k$ 不代表向量，而是代表有向的平面。只是在 $3 D$ 中每个平面都有一个唯一的法向量，所以我们经常滥用这种二元性。

But why are you identifying $i$ as $e_y e_z$ ? By Clifford algebra, Subhadeep Ray Commented Jan 15 at 19:44

但是你为什么要把 $i$ 识别为 $e_y e_z$ 呢？在 Clifford algebra 代数中，

$e_y e_z = e_y \cdot e_z + i |e_y \times e_z| = |e_y| |e_z| \exp(i \pi/2) = i$ .

It occurred to Hamilton during a walk to scratch into a bridge the following:

汉密尔顿在散步时想到在一座桥上刻下以下内容：

$i^2=j^2=k^2=ijk=-1$

From this we deduce by basic algebra:

我们通过基本代数推导出：

$ij = - ijkk = k$

$jk = - iijk = i$

$ki = - 1 jki = - 1$

$ki = - jjki = j$

$i^{-1} = -i^{-1}ijk = -jk = -i$

$j^{-1} = -j^{-1}jki = -ki = -j$

$k^{-1} = -ijkk^{-1} = -ij = -k$

$ji = j^{-1}i^{-1} = (ij)^{-1} = k^{-1} = -k$

$kj = - i$ similarly

$ik = - j$ similarly

So we can provide complete arithmetic operations for the set numbers of the form $a + ib + j c + k d$ :

所以我们可以为形式为 $a + ib + j c + k d$ 的集合数提供完整的算术运算：

$\begin{array}{l} (a + i b + j c + k d) \cdot (\alpha + i \beta + j \gamma + k \delta) \\ = a (\alpha + i \beta + j \gamma + k \delta) + i b (\alpha + i \beta + j \gamma + k \delta) + j c (\alpha + i \beta + j \gamma + k \delta) + k d (\alpha + i \beta + j \gamma + k \delta) \\ = a \alpha + i a \beta + j a \gamma + k a \delta + i b \alpha + i i b \beta + i j b \gamma + i k b \delta + j c \alpha + j i c \beta + j j c \gamma + j k c \delta + k d \alpha + k i d \beta + k j d \gamma + k k \delta \\ = (a \alpha - b \beta - c \gamma - d \delta) + i (a \beta + b \alpha + c \delta - d \gamma) + j (a \gamma - b \delta + c \alpha + d \beta) + k (a \delta + b \gamma - c \beta + d \alpha) \end{array}$

$\displaystyle \frac{1}{a + i b + j c + k d} = \frac{a - i b - j c - k d}{(a + i b + j c + k d)(a - i b - j c - k d)} = \frac{a - i b - j c - k d}{a^2 + b^2 + c^2 + d^2}$

via:

Quaternions: why does $ijk = - 1$ and $ij = k$ and $- ji = k$ - Mathematics Stack Exchange edited Apr 23, 2023 at 21:10（关于 $i\, j\, k = -1$ 的讨论）

https://math.stackexchange.com/questions/296349/quaternions-why-does-ijk-1-and-ij-k-and-ji-k

篇外二：关于布鲁姆大桥

Broome Bridge, Royal Canal, Broombridge Road, BALLYBOGGAN SOUTH, Dublin 7, DUBLIN

布鲁姆大桥，皇家运河，布鲁姆布里奇路， BALLYBOGGAN SOUTH，都柏林 7，都柏林

Survey Data 调查数据

Reg No	50060126
Rating	National
Categories of Special Interest	Architectural, Historical, Social, Technical
Original Use	Bridge
Date	1785 - 1850
Coordinates	313200, 237172
Date Recorded	16/08/2014
Date Updated	–/–/–

Description 描述

Two-arch limestone canal bridge of c.1790 and railway bridge of c.1845, carrying Broombridge Road on north-south axis over Royal Canal (north) and Dublin-Sligo railway line (south). Random coursed squared calp limestone walls with shallow piers flanking each arch having limestone ashlar plat-band to base of parapets and limestone ashlar coping. Elliptical arch to train bridge has rusticated limestone ashlar voussoirs and skewed squared calp soffit. Round arch to canal bridge has tooled limestone voussoirs and keystone with squared calp soffit. Canal bridge has Portland limestone plaque to northwest spandrel with inscription commemorating formula for quaternions devised by William Rowan Hamilton. Rubble stone embankment walls to either end have stacked coping. Break in east parapet provides access to steel footbridge to Broombridge Station. Tarmac carriageway follows steep gradient to both north and south approaches.
建于 1790 年的双拱石灰岩运河桥和建于 1845 年的铁路桥，南北轴线上承载着布鲁姆布里奇路，横跨皇家运河（北）和都柏林-斯莱戈铁路线（南）。随机的方形石灰石墙，每个拱门两侧都有浅桥墩，护墙底部有石灰石方石平台带和石灰石方石顶盖。通往火车桥的椭圆形拱门有质朴的石灰石方石拱腹和倾斜的方形 calp 拱腹。通往运河桥的圆拱有加工的石灰石拱门和带有方形 calp 拱腹的拱心石。运河桥的西北拱肩有波特兰石灰岩牌匾，上面刻有纪念威廉·罗文·汉密尔顿（William Rowan Hamilton）设计的四元数公式的铭文。两端的碎石路堤墙有堆叠的顶盖。东侧女儿墙的 Break 可通往 Broombridge 站的钢制人行天桥。柏油碎石车道沿着陡峭的坡度通往南北入口。

Appraisal 评价

Named after William Broome, a director of the Royal Canal Company. The canal section of the bridge is no doubt the older structure. It is of considerable significance for its associations with William Rowan Hamilton who. on the 16th October 1843, inscribed his mathematical formula for quaternions on to the bridge when out walking with his wife. The plaque under the bridge was unveiled by the Taoiseach Éamon de Valera, himself a mathematician and student of quaternions,on 13th November 1958. The railway bridge probably dates from the 1840s, while the two crossings now form a most appealing historic structure in the landscape at a junction of public transport and public amenity.
以皇家运河公司董事威廉·布鲁姆（William Broome）的名字命名。这座桥的运河部分无疑是较旧的结构。它与威廉·罗文·汉密尔顿（William Rowan Hamilton）的联系具有相当大的意义。1843 年 10 月 16 日，当他和妻子外出散步时，将他的四元数数学公式刻在了桥上。1958 年 11 月 13 日，桥下的牌匾由总理 Éamon de Valera 揭幕，他本人也是一位数学家和四元数的研究者。铁路桥的历史可能可以追溯到 1840 年代，而这两个道口现在在公共交通和公共设施的交界处形成了一个最具吸引力的历史建筑。