注:本文为 “信号频谱 | 幅度谱 / 相位谱 / 能量谱 / 功率谱” 相关文章合辑。
对第一篇原文略作重排。
信号频谱、幅度谱、相位谱及能量谱密度、功率谱密度
posted @ iliveido 2013-03-22 23:52
谱的英文原词为 “spectrum”,最初认为其类似于函数图象,但此理解并不准确。信号是时间的函数,然而不能简单将信号称作谱。实际上,谱是函数图像中的特定一类。提及谱,必然与频率相关,本文的创作源于对 Parseval 恒等式的好奇。
spectrum [ˈspektrəm]
n. 范围,幅度;光谱;波谱,频谱;余象
Parseval 恒等式是傅里叶变换的重要性质。傅里叶变换将信号从时域或空域转换到频域,进而产生频谱。由于这种变换,谱与频率之间存在着紧密的内在联系。
尽管本文旨在科普,但仍应具备理科文章的简洁性。老师曾指出,Parseval 恒等式的直观意义( intuitive sense)在于:傅里叶变换前后,原信号与频谱之间能量守恒。傅里叶变换后的频谱保留了原信号的全部信息,且傅里叶变换是可逆的,即一一对应关系。
此外,还有一个关于傅里叶变换的重要事实:高斯分布的密度函数 e − x 2 2 \large e^{-\frac {x^2}{2}} e−2x2 是唯一的傅里叶变换不变函数。高斯密度函数的一阶导数与哺乳动物视觉感知系统主视皮层简单细胞的感受野(cortical receptive field)结构相似。在泛函分析中,当 σ → ∞ \sigma \to \infty σ→∞ 时,高斯密度函数的极限是 delta - dirac 函数 δ ( x ) \delta (x) δ(x),即脉冲函数。在大学一年级数学分析课程中,高斯密度函数的积分为 π \sqrt {\pi} π。综上所述,高斯分布具有众多非常完美的性质。
回到主题,信号经傅里叶变换后产生频谱,频谱是以频率为自变量的函数。频谱在每个频率点的取值为复数,而复数由模和辐角唯一确定,即 z = r ( cos θ + i sin θ ) z = r (\cos\theta + i\sin\theta) z=r(cosθ+isinθ) 。因此,可将频谱分解为幅度谱(即复数的模关于频率的函数)和相位谱(即复数的辐角关于频率的函数)。
接下来探讨能量谱密度(energy spectral density)和功率谱密度(power spectral density)。起初以为 “energy” 和 “power” 都表示能量,实则 “power” 意为功率。在阐述这两个谱密度之前,先明确幅度的概念。
在英语中,“幅度” 有 “amplitude” 和 “magnitude” 两个词。在大多数情况下(包括本文),二者含义相同,仅在特定领域(如物理领域)存在差异:“amplitude” 表示整个信号偏离 x x x 轴的最大绝对值,“magnitude” 表示信号上某一点偏离 x x x 轴的绝对值。更详细的 阐述 如下:
peak amplitude, often shortened to amplitude, is the nonnegative value of the waveform’s peak (either positive or
negative).
peak amplitude,常简称为 amplitude,是波形峰值(正或负)的非负值。
instantaneous amplitude of x x x is the value of x ( t ) x(t) x(t) (either positive or negative) at time t t t.
instantaneous amplitude of x x x 是 x ( t ) x (t) x(t) 在时间 t t t 的值(正或负)。
instantaneous magnitude, or simply magnitude, of x x x is nonnegative and is given by ∣ x ( t ) ∣ |x (t)| ∣x(t)∣.
instantaneous magnitude,或简称为magnitude,是 x x x 的非负值,由 ∣ x ( t ) ∣ |x (t)| ∣x(t)∣ 给出。
由此可见,“amplitude” 是全局概念,“magnitude” 是瞬时概念。在讨论 FFT 和 wavelets 时,通常将 “amplitude” 和 “magnitude” 视为同一概念,即瞬时幅度。
信号 f ( t ) f (t) f(t) 在 t t t 处的瞬时幅度为 f ( t ) f (t) f(t) 的模,即 ∣ f ( t ) ∣ |f (t)| ∣f(t)∣;信号 f ( t ) f (t) f(t) 在 t t t 处的瞬时相位为 f ( t ) f (t) f(t) 的辐角,即 A r g f ( t ) Arg f (t) Argf(t) 或 ∠ f ( t ) \angle f (t) ∠f(t);信号 f ( t ) f (t) f(t) 在 t t t 处的瞬时功率为 f ( t ) f (t) f(t) 的模的平方,即 ∣ f ( t ) ∣ 2 |f (t)|^2 ∣f(t)∣2 。
信号的能量是全局概念,是瞬时功率的积分值,即:
∣ ∣ f ( t ) ∣ ∣ 2 = ∫ − ∞ ∞ ∣ f ( t ) ∣ 2 d t \large ||f (t)||^2=\int_{-\infty}^{\infty}|f (t)|^2 dt ∣∣f(t)∣∣2=∫−∞∞∣f(t)∣2dt
需注意 ∣ f ( t ) ∣ |f (t)| ∣f(t)∣ 和 ∣ ∣ f ( t ) ∣ ∣ ||f (t)|| ∣∣f(t)∣∣ 的区别:前者是瞬时概念,表示信号在某一点的瞬时幅度;后者是全局概念,表示整个信号能量的开方。
通常所指的能量谱和能量谱密度是同一概念;功率谱和功率谱密度是同一概念,且功率指平均功率。
时域上的能量公式
E ( f ) = ∫ − ∞ ∞ ∣ f ( t ) ∣ 2 d t E (f)=\int_{-\infty}^{\infty}|f (t)|^2 dt E(f)=∫−∞∞∣f(t)∣2dt
其中绝对值号代表取模,当信号为实信号时,绝对值号可去掉,公式变为:
E ( f ) = ∫ − ∞ ∞ f ( t ) 2 d t \large E (f)=\int_{-\infty}^{\infty} f (t)^2 dt E(f)=∫−∞∞f(t)2dt
根据 Parseval 能量恒等式(Parseval’s Identity),能量也可表示为 f ( t ) f (t) f(t) 的傅里叶变换的模的平方在频域上的积分。
频域上的能量公式
E ( f ) = ∫ − ∞ ∞ ∣ f ^ ( ω ) ∣ 2 d ω \large E (f)=\int_{-\infty}^{\infty}|\hat {f}(\omega)|^2 d\omega E(f)=∫−∞∞∣f^(ω)∣2dω
由上述积分可知,信号的能量谱密度在某个频率点上的取值即为信号在该频率上的瞬时功率 ∣ f ^ ( ω ) ∣ 2 |\hat {f}(\omega)|^2 ∣f^(ω)∣2 。
从上面的公式可以看出,信号的能量可能无穷大。当信号能量无限时,只能通过平均功率来分析该信号。因为能量 E ( f ) E (f) E(f) 与时间长度 △ T \triangle T △T 之比就是平均功率 P ( f ) P (f) P(f) ,即:
P ( f ) = E ( f ) △ T \large P (f)=\frac {E (f)}{\triangle T} P(f)=△TE(f)
易知:当信号在 t ∈ ( − ∞ , ∞ ) t \in (-\infty,\infty) t∈(−∞,∞) 的平均功率有限时,能量是无限的;当信号在 t ∈ ( − ∞ , ∞ ) t \in (-\infty,\infty) t∈(−∞,∞) 的能量有限时,其平均功率为 0。能量有限的信号称为能量信号;平均功率有限的信号称为功率信号。
为便于叙述,记:
f T ( t ) = { f ( t ) , ∣ t ∣ ≤ T 0 , ∣ t ∣ > T \large f_{T}(t)=\begin {cases} f (t)&, |t|\leq T\\ 0&, |t|>T \end {cases} fT(t)=⎩ ⎨ ⎧f(t)0,∣t∣≤T,∣t∣>T
则平均功率的公式为:
P ( f ) = lim T → ∞ ∫ − T T ∣ f T ( t ) ∣ 2 d t 2 T = lim T → ∞ ∫ − T T ∣ f T ^ ( ω ) ∣ 2 d ω 2 T \large P (f)=\lim_{T\to\infty}\frac {\int_{-T}^{T}|f_{T}(t)|^2 dt}{2T}=\lim_{T\to\infty}\frac {\int_{-T}^{T}|\hat {f_{T}}(\omega)|^2d\omega}{2T} P(f)=limT→∞2T∫−TT∣fT(t)∣2dt=limT→∞2T∫−TT∣fT^(ω)∣2dω
由上述积分可知,信号的功率谱密度为:
P S D ( f ) = lim T → ∞ ∣ f T ^ ( ω ) ∣ 2 2 T \large PSD (f) = \lim_{T\to\infty}\frac {|\hat {f_{T}}(\omega)|^2}{2T} PSD(f)=limT→∞2T∣fT^(ω)∣2
对于比信号更复杂的随机过程 X ( t ) X (t) X(t), P ( f ) P (f) P(f) 是一个随机变量,所以其平均功率 P P P 需取加权平均 E E E(此处 E E E 不是能量):
P = E [ P ( f ) ] = E [ lim T → ∞ ∫ − T T ∣ f T ^ ( ω ) ∣ 2 d ω 2 T ] = lim T → ∞ ∫ − T T E [ ∣ f T ^ ( ω ) ∣ 2 ] d ω 2 T \large P=E [P (f)]=E [\lim_{T\to\infty}\frac {\int_{-T}^{T}|\hat {f_{T}}(\omega)|^2d\omega}{2T}]=\lim_{T\to\infty}\frac {\int_{-T}^{T} E [|\hat {f_{T}}(\omega)|^2] d\omega}{2T} P=E[P(f)]=E[limT→∞2T∫−TT∣fT^(ω)∣2dω]=limT→∞2T∫−TTE[∣fT^(ω)∣2]dω
其功率谱密度为:
P S D = lim T → ∞ E [ ∣ f T ^ ( ω ) ∣ 2 ] 2 T \large PSD = \lim_{T\to\infty}\frac {E [|\hat {f_{T}}(\omega)|^2]}{2T} PSD=limT→∞2TE[∣fT^(ω)∣2]
参考文献
[1] Wikipedia. “Spectral Density”.
[2] Scott Miller & Donald Childers. “probability and random processes with applications to signal processing and communications”. section 10.1 Power Spectral Density.
一文读懂频谱、功率谱、能量谱、幅度谱、相位谱
平凡的兵 发布于 2023-05-25 15:59・IP 属地安徽
1. 什么是谱
牛顿奇迹年1666年,那年牛顿在老家躲避瘟疫,研究光学,大名鼎鼎的白光分解理论就是那时发现的,用 spectrum 表示谱,意思就是彩虹中的各种颜色。
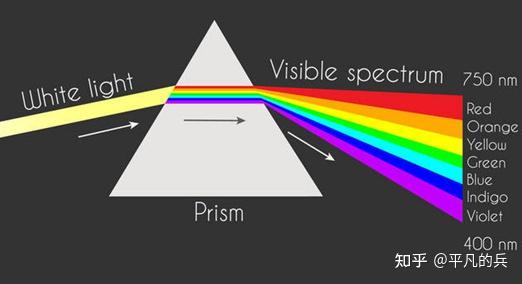
很遗憾,即使牛顿这样杰出的科学家,也没能继续发现不同光源其频率的不同。因为,牛顿是坚定的光粒子派。当然,如果牛顿发现了,也就没有下面的傅里叶啥事了。
太阳光信号可以分解为七种颜色的信号,同样,人的声音信号也可以分解为很多基础信号,傅里叶在信号处理领域大放异彩。
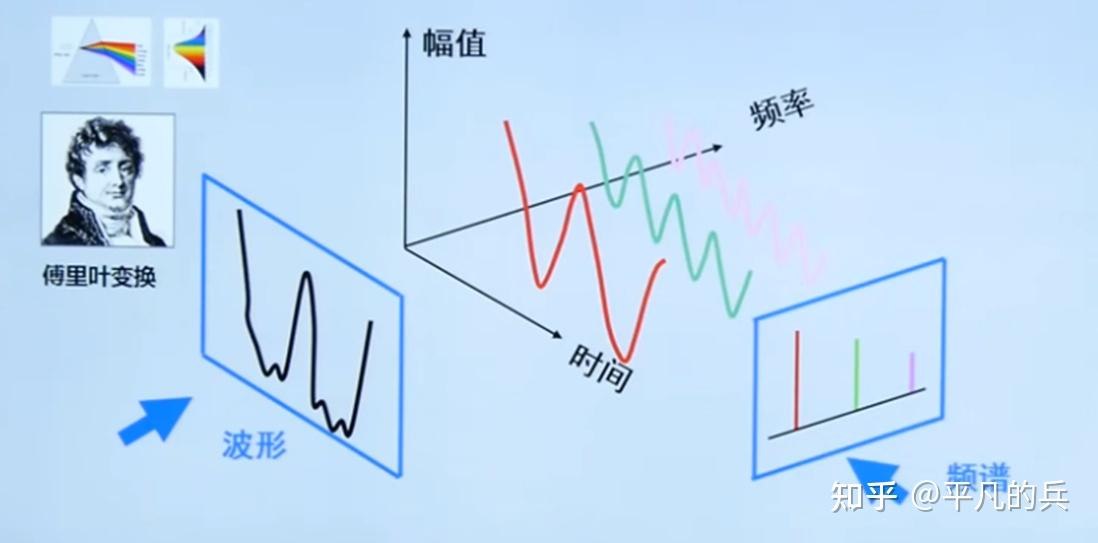
2. 概念大 PK
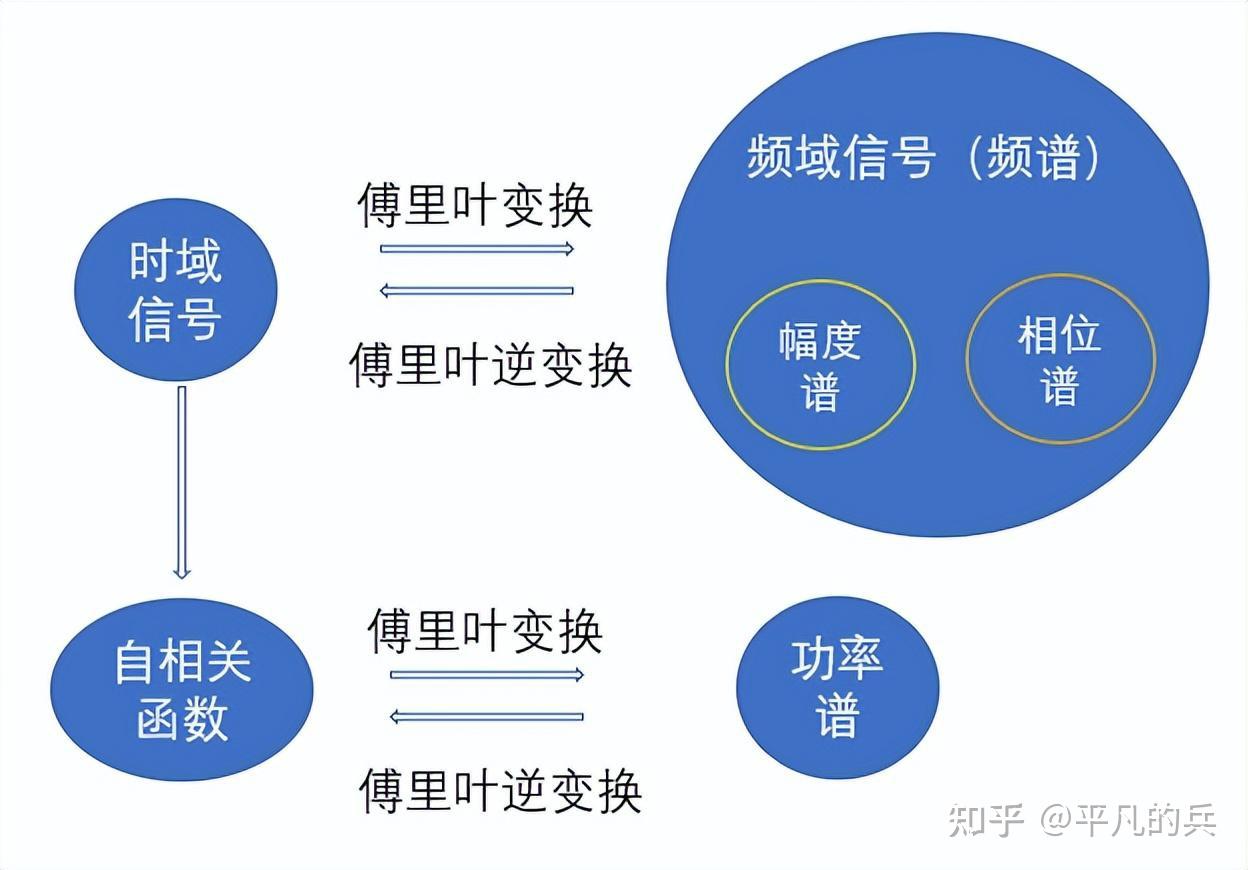

为什么引入功率谱?
对于功率信号,傅里叶变换不存在,所以引入功率谱概念,采用密度的概念,表示信号功率在各频率上的分布,对功率谱在频率上积分,可以得到信号功率。
这里为什么引入自相关函数 R x x Rxx Rxx,完成是因为计算的需要,自相关函数和功率谱互为傅里叶变换(维纳-辛钦定理)。具体证明可见参考书 [2].
3. 代码实践
生成一个随机信号x,绘制自相关曲线和功率谱曲线。
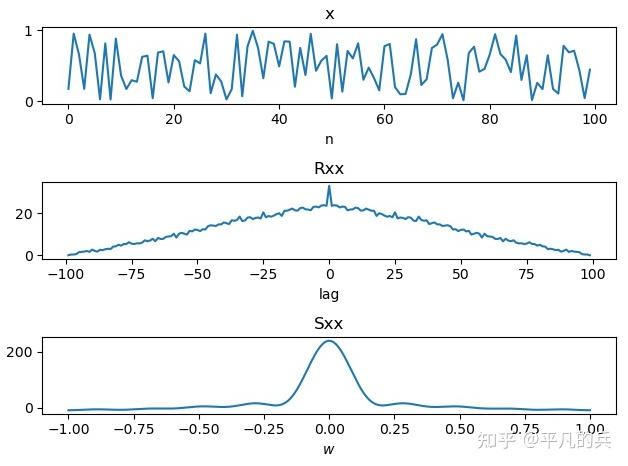
Python代码
import numpy as np
from numpy import sin,cos,pi
import matplotlib.pyplot as plt
import scipy.signal as sig
def PSD(Rx,maxlag,Nfft):
#PSD Computation of PSD using Autocorrelation Lags
# (Sx,omega) = PSD(Rx,lags,Nfft)
# Sx: Computed PSD values
# omega: digital frequency array in pi units from -1 to 1
# Rx: autocorrelations from -maxlag to +maxlag
# maxlag: maximum lag index (must be >= 10)
# Nfft: FFT size (must be >= 512)
Nfft2 = Nfft//2
M = 2*maxlag+1; # Bartlett window length
Rx = np.bartlett(M)*Rx[len(Rx)//2-maxlag+1:len(Rx)//2+maxlag+2] # Windowed autocorrelations
Rxzp = np.r_[np.zeros(Nfft2-maxlag),Rx,np.zeros(Nfft2-maxlag-1)]
Rxzp = np.fft.ifftshift(Rxzp) #Zero-padding and circular shifting
Sx = np.fft.fftshift(np.real(np.fft.fft(Rxzp))) # PSD
Sx = np.r_[Sx,Sx[1]] # Circular shifting
omega = np.linspace(-1,1,Nfft+1) # Frequencies in units of pi
return Sx, omega
if __name__ == '__main__':
x=np.random.rand(1,100);
maxlag = 10; #Load random sequence data
Rx = sig.correlate(x,x, mode='full')
lags = sig.correlation_lags(x.size, x.size, mode='full')
(Sx,omega) = PSD(Rx[0],maxlag,512); # Compute PSD
plt.subplot(311)
n=np.linspace(0,99,100)
plt.plot(n,x[0])
plt.title('x')
plt.xlabel('n')
plt.subplot(312)
plt.plot(lags,Rx[0])
plt.title('Rxx')
plt.xlabel('lag')
plt.subplot(313)
plt.plot(omega,Sx)
plt.title('Sxx')
plt.xlabel('$w$')
plt.tight_layout()
plt.savefig('psd.jpg')
Matlab 代码
function main
x=rand(1,100);
maxlag = 10; %Load random sequence data
[Rx,lags] = xcorr(x,maxlag,'coeff'); % Compute ACRS
[Sx,omega] = PSD(Rx,maxlag,512); % Compute PSD
subplot(311);
plot(x);
title('x');
xlabel('n');
subplot(312);
plot(lags,Rx);
title('Rxx');
xlabel('lag');
subplot(313);
plot(omega,Sx);
title('Sxx');
xlabel('\omega');
function [Sx,omega] = PSD(Rx,maxlag,Nfft)
%PSD Computation of PSD using Autocorrelation Lags
% [Sx,omega] = PSD(Rx,lags,Nfft)
% Sx: Computed PSD values
% omega: digital frequency array in pi units from -1 to 1
% Rx: autocorrelations from -maxlag to +maxlag
% maxlag: maximum lag index (must be >= 10)
% Nfft: FFT size (must be >= 512)
Nfft2 = Nfft/2;
M = 2*maxlag+1; % Bartlett window length
Rx = bartlett(M).*Rx(:); % Windowed autocorrelations
Rxzp = [zeros(Nfft2-maxlag,1);Rx;zeros(Nfft2-maxlag-1,1)];
Rxzp = ifftshift(Rxzp); %Zero-padding and circular shifting
Sx = fftshift(real(fft(Rxzp))); % PSD
Sx = [Sx;Sx(1)]; % Circular shifting
omega = linspace(-1,1,Nfft+1); % Frequencies in units of pi
4. 参考资料
[1] 深入浅出数字信号处理,江志红
[2] Digital signal processing using matlab, Fourth Edition, Vinay K. Ingle, John G. Proakis
via:
-
信号的频谱、幅度谱、相位谱及能量谱密度、功率谱密度 - 博客园 posted @ iliveido 2013-03-22 23:52
https://www.cnblogs.com/iliveido/archive/2013/03/22/2976542.html -
一文读懂频谱、功率谱、能量谱、幅度谱、相位谱 - 知乎 平凡的兵 发布于 2023-05-25 15:59・IP 属地安徽
https://zhuanlan.zhihu.com/p/632149690





















 7672
7672

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








