线性回归及逻辑回归算法相关推导与求导过程以及初步版本的练习代码

线性回归算法及逻辑回归算法相关推导

@(机器学习)[线性回归算法]

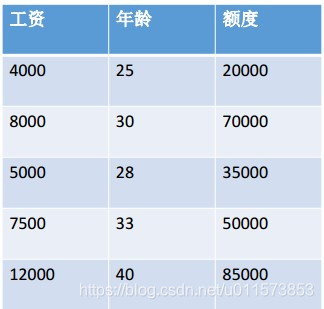
• 使用的数据

如下图所示是我们使用的案例数据

• 推论

如图是数据构成的平面

$X_1,X_2$是我们的两个特征(年龄和工资)，Y是银行最终会借给我们的多少钱。我们需要找到一个合适的线来拟合我们的数据，从而对我们未来的数据进行预测

假设${\theta }_1是年龄的参数，{\theta }_2是工资的参数。假设H_{\theta }(x)={\theta }_0+{\theta }_1{x}_1+{\theta }_2{x}_2（其中{\theta }_0为偏置项）$.我们的任务就是利用数据进行训练找到最适合的${\theta }_0,{\theta }_1,{\theta }_2$

• 利用矩阵进行表示$H_{\theta }(x)$

$$\theta =\left[\begin{array}{c}{\theta }_0\\ {\theta }_1\\ {\theta }_2\end{array}\right]$$
$$X=\left[\begin{array}{c}{x}_0\\ x_1\\ x_2\end{array}\right]$$
其中$x_0=1$
$则H_{\theta }(x)可以变成$
$$H_{\theta }(x)={\theta }_0{x}_0+{\theta }_1{x}_1+{\theta }_2{x}_2=\sum _{i=0}^2{\theta }_i{x}_i={\theta }^{T}X$$

• 误差

真实值和预测值之间肯定是要存在差异的
（用 $ϵ$来表示该误差）
则对于每一个样本来说$$y^i={\theta }^T{X}^i+{ϵ}^i\text{\hspace{1em}(1)}$$
$由于误差ϵ是独立并且有相同的分布，并且服从均值为0，方差为{\theta }^2的高斯分布所以p({ϵ}^i)为$
$$p({ϵ}^i)=\frac{1}{\sqrt{2\pi }\sigma }{e}^{-\frac{({ϵ}^i-\mu {)}^2}{2{\sigma }^2}}其中\mu =0所以p({ϵ}^i)=\frac{1}{\sqrt{2\pi }\sigma }{e}^{-\frac{({ϵ}^i{)}^2}{2{\sigma }^2}}\text{\hspace{1em}(2)}$$
$$由(1)式可知\Rightarrow {ϵ}^i=y^i-{\theta }^T{X}^i\text{\hspace{1em}(3)}$$
$$把(3)试带入(2)得\Rightarrow p(y^i|X^i;\theta )=\frac{1}{\sqrt{2\pi }\sigma }{e}^{-\frac{(y^i-{\theta }^T{X}^i{)}^2}{2{\sigma }^2}}\text{\hspace{1em}(4)}$$

$目前我们有了数据和模型需要去求使得更符合真实数据的参数\theta ,便可以使用极大似然对参数\theta 进行求解$

• 似然函数

$$L(\theta )=\prod _{i=1}^{m}p(y^i|X^i;\theta )=\prod _{i=1}^m\frac{1}{\sqrt{2\pi }\sigma }{e}^{-\frac{(y^i-{\theta }^T{X}^i{)}^2}{2{\sigma }^2}}$$
为使计算更加方便对似然函数取对数
$$\ln L(\theta )=\ln \prod _{i=1}^m\frac{1}{sqrt2\pi \sigma }{e}^{-\frac{(y^2-{\theta }^T{X}^i{)}^2}{2{\sigma }^2}}=\sum _{i=1}^m\ln \frac{1}{\sqrt{2\pi }\sigma }{e}^{-\frac{(y^i-{\theta }^T{X}^i{)}^2}{2{\sigma }^2}}$$
展开以后得:
$$m\ln \frac{1}{sqrt2\pi \sigma }-\frac{1}{{\sigma }^2}\ast \frac{1}{2}\sum _{i=1}^m(y^i-{\theta }^T{X}^i{)}^2$$

目标是让似然函数越大越好所以可以使$J(\theta )=\frac{1}{2}{\sum }_{i=1}^m(y^i-{\theta }^T{X}^i{)}^2$越小越好.

• 目标函数

$$J(\theta )=\frac{1}{2}\sum _{i=1}^m(H_{\theta }(X^i)-y^i{)}^2=\frac{1}{2}(X\theta -y{)}^T(X\theta -y)$$
因为在矩阵中$a^2=a^T\ast a$
对目标函数进行求导
$${\nabla }_{\theta }J(\theta )={\nabla }_{\theta }(\frac{1}{2}(X\theta -y{)}^T(X\theta -y))={\nabla }_{\theta }(\frac{1}{2}({\theta }^T{X}^T-y^T)(X\theta -y))={\nabla }_{\theta }(\frac{1}{2}({\theta }^2{X}^{T}X\theta -{\theta }^T{X}^{T}y-y^{T}X\theta +y^{T}y))=\frac{1}{2}(2X^{T}X\theta -X^{T}y-(y^{T}X{)}^T)=X^{T}X\theta -X^{T}y$$

$使偏导等于0可以得\Rightarrow \theta =(X^{T}X{)}^{-1}{X}^{T}y注意只有在（X^{T}X）可逆得时候此方法才可以使用$

• 机器学习各种评估方法

1、标准化
对于多元线性回归需要对各个自变量进行标准化，排除单位的影响。
标准化方法：即将原始数据减去相应变量的均数后再除以该变量的标准差，而标准化得到的回归方程称为标准化回归方程，相应得回归系数为标准化回归系数。
2、T检验
T检验是对各个回归系数的检验，绝对值越大，sig就越小，sig代表t检验的显著性，在统计学上，sig<0.05一般被认为是系数检验显著，显著的意思就是你的回归系数的绝对值显著大于0，表明自变量可以有效预测因变量的变异，做出这个结论你有5%的可能会犯错误，即有95%的把握结论正确。
3、F检验
F检验是对所有回归系数的检验，代表你进行回归的所有自变量的回归系数的一个总体检验，如果sig<0.05,说明至少有一个自变量能够有效预测因变量，这个在写数据分析结果时一般可以写出。
F检验和R平方同向变化，当R方=0时F=0；
当R方越大，F值也就越大
当R方=1时，F为无穷大。
F检验是所有回归系数的总显著性的度量也是R方的显著性检验，即检验回归系数为0 等价于R方为0，也就是在计算R方后，就不必做F检验。
另外对于一元线性回归，F检验等价于T检验，因为回归系数只有一个。
4、R方
对于每组数据，我们可以用最小二乘法来求得一个线性模型，但对于这个模型的效果如何，如何来比较模型之间的好坏呢。R方就是来处理这个问题，它可以来计算预测值和真实y值的匹配程度，当R方（0~1）越接近1，这线性关系越明显。
而在使用的时候要用调整后的R方，这个值是针对自变量的增多会不断增强预测力的一个矫正（因为即使没什么用的自变量，只要多增几个，R方也会变大，调整后的R方是对较多自变量的惩罚），R可以不用管，标准化的情况下R也是自变量和因变量的相关
$$R^2=1-\frac{{\sum }_{i=1}^m(\widehat{y_i}-y_i{)}^2(残差平方和)}{{\sum }_{i=1}^m(y_i-\tilde{y}{)}^2(类似方差项)}$$
$R^2越接近1就认为模型拟合的越好$

• 梯度下降

1.引入原因:当我们得到了目标函数以后只有当$（X^{T}X）$可逆的时候才可以直接求得当$（X^{T}X）$不可逆的时候就要使用梯度下降算法一点点的求出合适的$\theta$值
2.背后思想:开始时会随机选择一组参数组合$({\theta }_0,{\theta }_1,...,{\theta }_n)$,计算出d代价函数，然后找下一个能让代价函数值下降最多的参数组合。持续这么做直到找到一个局部最小值.
3.什么是梯度下降如下图所示

在进行使用梯度进行求解参数时是对每一个${\theta }_i$进行单独进行求偏导，必须保证同步更新。
4.目标函数:
$$J(\theta )=\frac{1}{2m}\sum _{i=1}^m(h_{\theta }(x^{(i)})-y^{(i)}{)}^2$$
我们得目标就是使得目标函数$J(\theta )$得值最小，也就是使得平均误差平方值最小。所以我们要使得目标函数得倒数为0.
5.对$J(\theta )$求导
$$\frac{\sigma }{\sigma {\theta }_j}J(\theta )=\frac{\sigma }{\sigma {\theta }_j}(\frac{1}{2m}\sum _{i=1}^m(h_{\theta }(x^{(i)})-y^{(i)}{)}^2)$$
$$=\frac{1}{2m}\sum _{i=1}^{m}2(h_{\theta }(x^{(i)})-y^{(i)})\frac{\sigma }{\sigma {\theta }_j}(h_{\theta }(x^{(i)})-y^{(i)})$$
$$=\frac{1}{m}\sum _{i=1}^m(h_{\theta }(x^{(i)})-y^{(i)})\frac{\sigma }{\sigma {\theta }_j}{h}_{\theta }(x^{(i)})$$
$$=\frac{1}{m}\sum _{i=1}^m(h_{\theta }(x^{(i)})-y^{(i)})\frac{\sigma }{\sigma {\theta }_j}({\theta }_0{x}_0^{(i)}+{\theta }_1{x}_1^{(i)}+...+{\theta }_m{x}_m^{(i)})$$
$$=\frac{1}{m}(h_{\theta }(x^{(i)})-y^{(i)})x_j^{(i)}$$
所在在更新是的时候进行一下步骤
Repat{
${\theta }_j$ :=${\theta }_j$-$\alpha \frac{1}{m}{\sum }_{i=1}^m(h_{\theta }(x^{(i)})-y^{(i)})\ast x_j^{(i)}$
} 要保证同步更新
6.梯度下降步骤

下山分以下步走（更新参数）
（1）：找到当前最合适的方向
（2）：走那么一小步，走快了该” 跌倒 ” 了
（3）：按照方向与步伐去更新我们的参数

7.梯度下降方式

1.批量梯度下降：$$\frac{\sigma J(\theta )}{\sigma {\theta }_j}=-\frac{1}{m}\sum _{i=1}^m(h_{\theta }(x^{(i)})-y^{(i)})$$
${\theta }_j={\theta }_j-\alpha \frac{1}{m}{\sum }_{i=1}^m(h_{\theta }(x^{(i)})-y^{(i)})x_j^{(i)}$
（容易得到最优解，但是由于每次考虑所有样本，速度很慢）

2.随机梯度下降:${\theta }_j={\theta }_j-(h_{\theta }(x^{(i)})-y^{(i)})x_j^{(i)}$
（每次找一个样本，迭代速度快，但不一定每次都朝着收敛的方向）
3.小批量梯度下降法:${\theta }_j={\theta }_j-\alpha \frac{1}{10}{\sum }_{k=i}^{i+9}(h_{\theta }(x^{(k)})-y^{(k)})x_j^{(k)}$
（每次更新选择一小部分数据来算,上面公式是每次选择10条数据进行更新）

8.学习速率$\alpha$得选择:

如果$\alpha$过小会导致更新速度特别慢，如果过大就有可能导致无法找到最小值点。如下图所示

9.批处理得数量:32，64，128，一般要考虑内存和效率

• 逻辑回归

1.注意

:逻辑回来是一种分类得算法，经典得二分类算法，也可以用于多分类
机器学习算法选择：先逻辑回归再用复杂的，能简单还是用简单的

2.机器学习算法选择

先逻辑回归再用复杂的，能简单还是用简单的

3.逻辑回归的决策边界

可以是非线性得，及多维得

4.Sigmoid函数

1.公式为：
$$g(z)=\frac{1}{1+e^{-z}}其中z就是线性回归中得输入值{\theta }^{T}X$$
也可以把一些线性回归得问题用逻辑回归进行求解
2.函数图

自变量取值为任意实数，值域[0,1]
解释：将任意的输入映射到了[0,1]区间我们在线性回归中可以得到一个预测值，再将该值映射到Sigmoid 函数中这样就完成了由值到概率的转换，也就是分类任务

5.预测函数:

$$h_{\theta }(x)=g({\theta }^{T}x)=\frac{1}{1+e^{-{\theta }^{T}x}}(其中{\theta }^{T}x=\sum _{i=1}^n={\theta }_0{x}_0+{\theta }_1{x}_1+...+{\theta }_n{x}_n)$$

6.分类任务:

$$P(y=1|x;\theta )=h_{\theta }(x)\text{\hspace{1em}(1)}$$
$$P(y=0|x;\theta )=1-h_{\theta }(x)\text{\hspace{1em}(2)}$$
$由(1)(2)可以整合为\Rightarrow P(y|x;\theta )=(h_{\theta }(x){)}^y(1-h_{\theta }(x){)}^{1-y}$
对于二分类任务(0,1),整合后y取0只保留$(1-h_{\theta }(x){)}^{1-y}$y取1只保留$(h_{\theta }(x){)}^y$

7.似然函数

与线性回归里面引入似然函数一样，都是为了求取最合适得参数
似然函数:$$L(\theta )=\prod _{i=1}^{m}P(y_i|x_i;\theta )=\prod _{i=1}^m(h_{\theta }(x_i){)}^{y_i}(1-h_{\theta }(x_i){)}^{1-y_i}$$
对数似然:$$l(\theta )=\log L(\theta )=\log \prod _{i=1}^m(h_{\theta }(x_i){)}^{y_i}(1-h_{\theta }(x_i){)}^{1-y_i}$$
$$=\sum _{i=1}^m(y_i\log h_{\theta }(x_i)+(1-y_i)\log (1-h_{\theta }(x_i)))$$
此时的梯度函数是上升求最大值，引入$J(\theta )=-\frac{1}{m}l(\theta )$

8.对$J(\theta )$求导

在开始求导之前先交代一些东西如下为方便去掉i小标:
$$h_{\theta }(x)=g({\theta }^{T}x)=\frac{1}{1+e^{-{\theta }^{T}x}}\text{\hspace{1em}(1)}$$
$$\frac{\sigma }{\sigma \theta }{h}_{\theta }(x)=\frac{\sigma }{\sigma \theta }g({\theta }^{T}x)=\frac{\sigma }{\sigma \theta }\frac{1}{1+e^{-{\theta }^{T}x}}$$
$$=-\frac{(1+e^{-{\theta }^{T}x}{)}^{‘}}{(1+e^{-{\theta }^{T}x}{)}^2}=\frac{(e^{-{\theta }^{T}x})}{(1+e^{-{\theta }^{T}x}{)}^2}\frac{\sigma }{\sigma \theta }({\theta }^{T}x)$$
$$=\frac{1}{1+e^{-{\theta }^{T}x}}\frac{e^{-{\theta }^{T}x}}{1+e^{-{\theta }^{T}x}}\frac{\sigma }{\sigma \theta }({\theta }^{T}x)$$
$$=\frac{1}{1+e^{-{\theta }^{T}x}}(1-\frac{1}{1+e^{-{\theta }^{T}x}})\frac{\sigma }{\sigma \theta }({\theta }^{T}x)$$
$$=h_{\theta }(x)(1-h_{\theta }(x))\frac{\sigma }{\sigma \theta }({\theta }^{T}x)\text{\hspace{1em}(2)}$$
对$J(\theta )$进行求导
$$\frac{\sigma }{\sigma {\theta }_j}J(\theta )=\frac{\sigma }{\sigma {\theta }_j}(-\frac{1}{m}\sum _{i=1}^m(y^i\log h_{\theta }(x^i)+(1-y^i)\log (1-h_{\theta }(x^i))))$$
$$=-\frac{1}{m}\frac{\sigma }{\sigma {\theta }_j}(\sum _{i=1}^m(y^i\log h_{\theta }(x^i)+(1-y^i)\log (1-h_{\theta }(x^i))))$$
$$=-\frac{1}{m}\sum _{i=1}^m(y^i\frac{1}{h_{\theta }(x^i)}\frac{\sigma }{\sigma {\theta }_j}{h}_{\theta }(x^i)+(1-y^i)\frac{1}{1-h_{\theta }(x^i)}\frac{\sigma }{\sigma {\theta }_j}(1-h_{\theta }(x^i)))$$
$$=-\frac{1}{m}\sum _{i=1}^m(y^i\frac{1}{h_{\theta }(x^i)}\frac{\sigma }{\sigma {\theta }_j}{h}_{\theta }(x^i)-(1-y^i)\frac{1}{1-h_{\theta }(x^i)}\frac{\sigma }{\sigma {\theta }_j}{h}_{\theta }(x^i))$$
$$=-\frac{1}{m}\sum _{i=1}^m((y^i\frac{1}{h_{\theta }(x^i)}-(1-y^i)\frac{1}{1-h_{\theta }(x^i)})\frac{\sigma }{\sigma {\theta }_j}{h}_{\theta }(x^i))$$
把(2)式代入得
$$=-\frac{1}{m}\sum _{i=1}^m((y^i\frac{1}{h_{\theta }(x^i)}+(1-y^i)\frac{1}{1-h_{\theta }(x^i)})h_{\theta }(x^i)(1-h_{\theta }(x^i))\frac{\sigma }{\sigma {\theta }_j}({\theta }^T{x}^i))$$
$$=-\frac{1}{m}\sum _{i=1}^m((y^i\frac{1}{h_{\theta }(x^i)}+(1-y^i)\frac{1}{1-h_{\theta }(x^i)})h_{\theta }(x^i)(1-h_{\theta }(x^i))\frac{\sigma }{\sigma {\theta }_j}({\theta }^T{x}^i))$$
$$=-\frac{1}{m}\sum _{i=1}^m(y^i-y^i{h}_{\theta }(x^i)-h_{\theta }(x^i)+y^i{h}_{\theta }(x^i))\frac{\sigma }{\sigma {\theta }_j}({\theta }^T{x}^i))$$
$$=\frac{1}{m}\sum _{i=1}^m(h_{\theta }(x^i)-y^i)\frac{\sigma }{\sigma {\theta }_j}({\theta }_0{x}_0+{\theta }_1{x}_1+...+{\theta }_m{x}_m))$$
$$=\frac{1}{m}\sum _{i=1}^m(h_{\theta }(x^i)-y^i)x_j^i)$$

9.参数更新

${\theta }_j:={\theta }_j-\alpha \frac{1}{m}{\sum }_{i=1}^m(h_{\theta }(x^i)-y^i)x_j^i$
10.多分类得softmax:$$h_{\theta }(x^i)=\left[\begin{array}{c}p(y^{(i)}=1|x^{(i)};\theta )\\ p(y^{(i)}=2|x^{(i)};\theta )\\ .\\ p(y^{(i)}=k|x^{(i)};\theta )\end{array}\right]=\frac{1}{{\sum }_{j=1}^k{e}^{{\theta }_j^T{x}^{(i)}}}\left[\begin{array}{c}{e}^{{\theta }_1^T{x}^{(i)}}\\ e^{{\theta }_2^T{x}^{(i)}}\\ .\\ e^{{\theta }_k^T{x}^{(i)}}\end{array}\right]$$

• 代码实现逻辑回归的基本流程

1.读数据
path = “M:/python练习/data/Python/LogiReg_data.txt”
paData = pd.read_csv(path, header=None)
2.处理数据
# 为x加上一列 全为1
paData.insert(0, ‘Ones’, 1)
变成矩阵
orig_data = paData.as_matrix()
cols = orig_data.shape[1]
提取X与Y
X = orig_data[:, 0:cols - 1]
y = orig_data[:, cols - 1:cols]
构造theta
theta = np.zeros([1, 3])

3.完成以下模块

1.sigmoid：映射到概率得函数
2.model :返回预测结果值
3.cost ：根据参数计算损失
4.gradient :计算每一个参数得梯度方向
5.descent: 进行参数更新
6.accuracy:计算精度

4.sigmoid：映射到概率得函数

对应的公式$$h_{\theta }(x)=g(z)=\frac{1}{1+e^{-z}}（其中z={\theta }^{T}x）$$
对应代码为
def sigmoid(z): return 1/(1+np.exp(-z))

5.model :返回预测结果值 类似与h(x)
对应代码

def model(X,theta): return sigmoid(np.dot(X,theta.T)) np.dot(A,B)是求A与B的成绩

6.cost ：根据参数计算损失

对应公式
$$J(\theta )=-\frac{1}{m}\sum _{i=1}^m(y_i\log h_{\theta }(x_i)+(1-y_i)\log (1-h_{\theta }(x_i)))$$
对应代码
def cost(X,y,theta): left = np.multiply(-y,np.log(model(X,theta))) right = np.multiply(1-y,np.log(1-model(X,theta))) return np.sum(left-right)/(len(X))

7.gradient :计算每一个参数得梯度方向

对应公式
$$\frac{1}{m}\sum _{i=1}^m(h_{\theta }(x^i)-y^i)x_j^i$$
对应代码
def gradient(X,y,theta): grad = np.zeros(theta.shape) error = (model(X,theta)-y).ravel() for j in range(len(theta.ravel())): term = np.multiply(error,X[:,j]) grad[0,j] = np.sum(term)/len(X) return grad

8.descent: 进行参数更新

对应公式$${\theta }_j:={\theta }_j-\alpha \frac{1}{m}\sum _{i=1}^m(h_{\theta }(x^i)-y^i)x_j^i$$
对应代码
import time def descent(data,theta,batchSize ,stopType,thresh,alpha): #batchSize 一次取数据得大小 thresh 策略对应得阈值 init_time = time.time() grad = np.zeros(theta.shape) i=0 #迭代次数 k=0 #batch X,y = shuffleData(data) n=X.shape[0] costs = [cost(X,y,theta)] while True: grad = gradient(X[k:k+batchSize],y[k:k+batchSize],theta) k+=batchSize #取batch数量得数据 if k >=n: #k超过得总得数据大小 k=0 X,y = shuffleData(data) theta = theta-alpha*grad costs.append(cost(X,y,theta)) #计算新得损失 i+=1 if stopType==STOP_ITER: value=i elif stopType==STOP_COST:value=costs elif stopType==STOP_GRAD: value=grad if stopCriterion(stopType,value,thresh):break return theta,i-1,costs,grad,time.time()-init_time

9.预测与精度

#进行预测 def predict(X,theta): return [1 if x>0.5 else 0 for x in model(X,theta)] #进行精度 def accuracy(pre,y): correct=[1 if ((a==1 and b==1)or (a==0 and b ==0))else 0 for (a,b) in zip(pre,y)] accuracy = (sum(map(int,correct))% len(correct)) print('accuracy = {0}%'.format(accuracy))

10.其他依赖函数

STOP_ITER = 0 #迭代次数 STOP_COST = 1 #根据损失函数得值 STOP_GRAD = 2 # def stopCriterion(stype,value,threshold): if stype==STOP_ITER: return value>threshold elif stype==STOP_COST: print(abs((value[-1]-value[-2]))) return abs((value[-1]-value[-2]))<threshold elif stype==STOP_GRAD: return np.linalg.norm(value)<threshold #数据洗牌,打乱数据 def shuffleData(data): np.random.shuffle(data) clos = data.shape[1] X= data[:,0:clos-1] y= data[:,clos-1:clos] return X,y

---

本人初步学习，记录只是为了方便自己查阅，记录过程也是方便自己理解。若有错误还望广大网友指点。谢谢