费马小定理的两个证明方法(群论和构造项链法)_费马小定理的组合证明-优快云博客

费马小定理

若p是素数，对任何满足0<a<p的整数a，都有 $a^{p-1}-1$ 能被p整除，记作 $p|(a^{p-1}-1)$ .

群论证明法

证明:考虑整数模p乘法群，这个群的元素由所有模p的非零余数构成，并且要求与p互素，因为p是素数，所以这个群的元素为1,2,...,p-1.单位元e=1.群的阶p-1.根据拉格朗日定理，群的每个元素都有有限的阶k（抽屉原理）并且整除大群的阶p-1.所以：

$a^{p-1}=a^{\frac{p-1}{k}*k}=(a^k)^\frac{p-1}{k}=e^{\frac{p-1}{k}}=e, k \in Z$

而在模p乘法群中，e也就是单位元1，按照模p乘法群的计算法则，这也结论也就是：

$a^{p-1}\equiv 1\ mod\ p$

因此 $p|(a^{p-1}-1)$ .

除了数对2，3，不存在连续两个自然数都是素数的情况（因为必然有一个是偶数，存在因子），也就是2，3是唯一的一组连续素数，并且2是唯一的一个偶素数。对于p=2的情况，a=1. 那么：

$1^{2-1} -1=1-1=0$

0整除2.

对于p=3,a=2:

$2^{3-1}-1=4-1=3$

也满足定理。

存在插值为2的两个连续自然数均为素数，如果p,p+2都是素数，它们构成了一对孪生素数，比如：

(3,5),(5,7),(11,13),(17,19),(29,31)等。

一个著名猜想是：是否存在无限多个孪生素数？目前数学家们倾向于这个猜想是正确的，但尚未被严格证明。

如果放宽条件，考虑三个连续的奇数都是素数，那么唯一的情况是(3,5,7),因为对于任何其他三个连续奇数(n,n+2,n+4)，其中至少有一个是3的倍数。

对于唯一的连续两个自然数是素数情况2和3，整数模3乘法群是2阶群C2，它是2阶循环群，而3阶群也是循环群C3，所以循环群和2，3数对对应。

构造项链法

构造法可以提供更加符合直觉的证明，也更加有趣，类似于思想实验，需要对问题的深刻理解和洞察。证明过程如下：

考虑有a种不同颜色的珍珠，我们要串一条长p的珍珠串，其中p为素数，我们要求a<p以便于用上所有的颜色。显然，根据排列组合知识一共存在有 $a^p$ 种可能的不同的串，因为串中每个位置都可以在a种颜色的珍珠中选择，共选择p次。

例如有红色（用A表示）和绿色（用B表示）两种颜色的珍珠，要串长度为5的串，即a=2,p=5.一共有 $2^5=32$ 种不同的串，如下图所示，对应：红红红红红，红红红红绿，。。。绿绿绿绿红，绿绿绿绿绿。

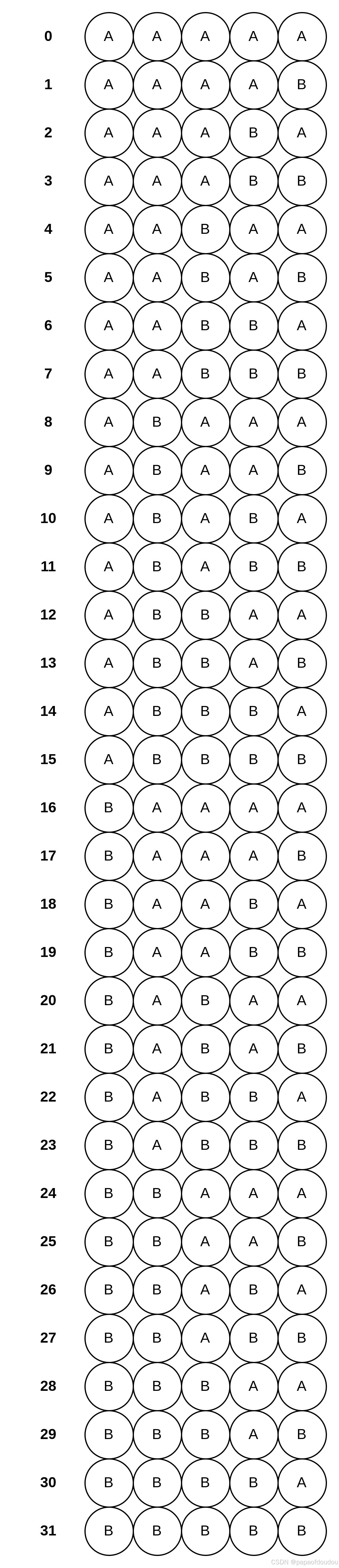
并且，这 $a^p$ 串珍珠中，一定存在a个颜色完全相同的串（每种颜色一条有唯一一条同色的串，比如上面的例子，红绿两种颜色有红红红红红和绿绿绿绿绿两条同色串）。

现在要证明，在组成的这 $a^p$ 个珍珠串中，如果去掉这a个同色的，剩下的 $a^p-a$ 串珍珠可以分成若干组，每组恰好有p串珍珠，这样如果 $p|({a^p-a})$ ，因为a和p互素，所以只能是 $p|({a^{p-1}-1})$ .问题即被证明。

此外，如果把每串珍珠首尾连接起来做成项链，原来有些不同的串会变成相同的项链，如果一个串可以通过旋转变换成另一个，这两个串必然做成相同的项链，如下图所示，串的轮换有5种情况，但是最终作成的项链只有一种。

一个项链拆开后可以代表多少中不同的串呢？如果一个串S由若干的相同的子串复制连接而成，而子串内部无法在找到相同模式的串无法继续拆分，假设子串有M个珍珠，则由S构成的项链可以代表M种不同的串，例如串：S=ABBABBABBABB，由相同的子串M=ABB复制多次而成，如果我们一次旋转一颗珍珠，一共可以得到三串不同的结果：

ABBABBABBABB，BBABBABBABBA，BABBABBABBAB，ABBABBABBABB(开始重复)，

除去这三种之外，不可能再有其他不同类的串了，ABB的长度为3，再次轮换得到相同的结果，这样，所有的 $a^p$ 串珍珠可以分成两类，一类是a串颜色相同的串，各对应一种项链。另一类是颜色不同，但是由这些串的长度p是素数，它绝不可能由若干个子串复制连接出来（相当于子串就是整个串的长度），所以任何一种这样的项链，总共代表p个这样不同的串，这些串可以通过彼此的轮换得到。而这样的串有 $a^p-a$ 种。连成项链后分组，每一组恰好p个串，代表一种不同的项链。

要知道不可能存在半条项链，项链的拓展是由所有珍珠的排列组合构成的串开始的，所以如果存在一条项链，则对应的串一定有p个，要么就没有对应的项链。、

所以 $a^p-a=a(a^{p-1}-1)$ 就是构成这些存在不同颜色的项链的串的数量，这些串儿可以做成