llama3-70B几个问题答疑

NVIDIA LLAMA3-70B大模型体验地址：

NVIDIA NIM | llama3-70b

问题几个关于宇宙的问题，答案挺有意思的，很有启发性，记录一下：

问题1：既然相对论认为时间是相对的，为何却说宇宙寿命有137亿年？

问题2：对于黑洞来说，大爆炸是不是刚刚发生不久的事情？

问题3：对于光来说，大爆炸是刚刚发生的事情么？

普通PC的USB控制器都是通过PCIE扩展的么?

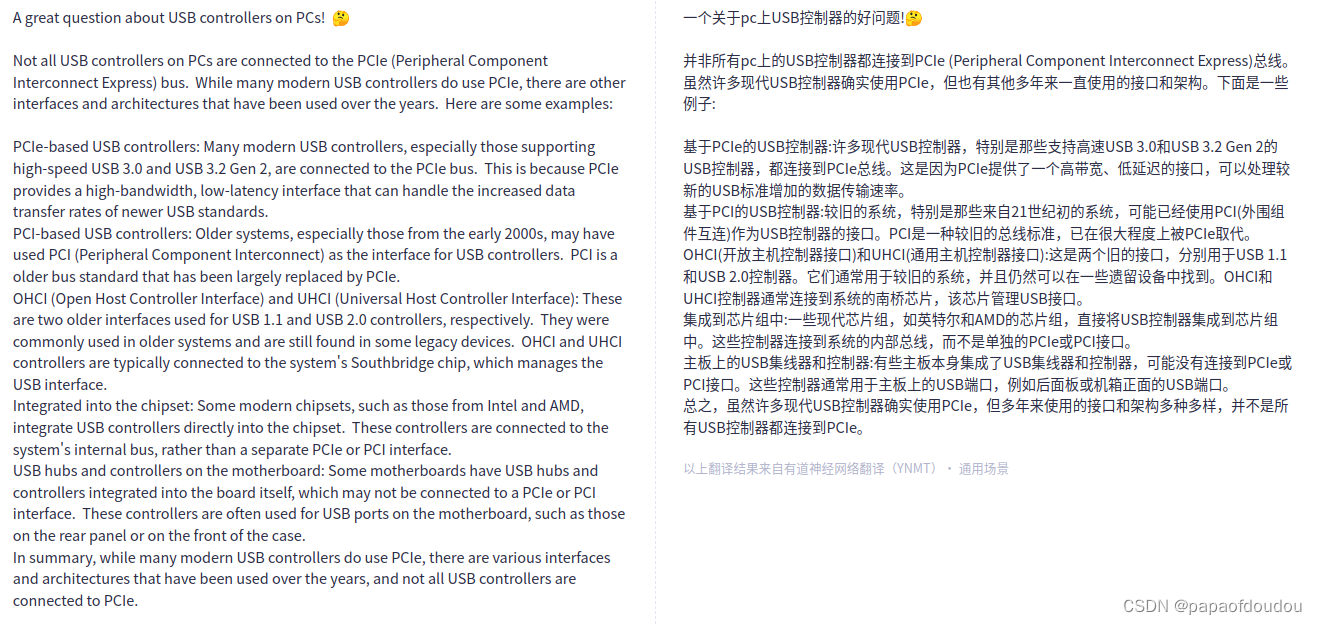
为什么服务器系统广泛通过PCIe接口扩展功能，而非使用内部总线？

请评价如下用经典力学理解相对论时间膨胀的方法：如果一个物理运动速度接近光速，则物体上的任何一个质点，包括电子的运动速度都会接近光速，所以，电子的实际速度是物理运动速度和电子自身振动速度的矢量和，而因为光速是固定的，所以物体接近光速运动必然导致电子振动速度变慢，时间流逝是由电子震荡速度决定的，所以高速运动的物体时间会变慢，这样理解对吗?

看来，凡人很难企及到理解相对论的高度。

可以多个处理器核执行同一个线程么？

超标量流水线一定要求有多条流水线么?

多发射要求多流水线，超标量只要执行阶段有多个执行单元就可以了，并不要求一定是多条流水线。一条流水线也可以被设计为多发射，在单个时钟周期中发射和执行多条指令。

超标量流水线一定要求有多条流水线么

A great question about superscalar pipelines! 🚀

No, a superscalar pipeline does not necessarily require multiple pipelines. In fact, a superscalar pipeline can be implemented using a single pipeline with multiple execution units.

In a superscalar pipeline, the processor can execute more than one instruction in a single clock cycle. This is achieved by having multiple execution units, such as arithmetic logic units (ALUs), load/store units, and branch units, that can operate concurrently.

There are several ways to implement a superscalar pipeline:

Multiple execution units: A single pipeline with multiple execution units, each capable of executing a different instruction. For example, a processor might have two ALUs, two load/store units, and a branch unit, allowing it to execute up to three instructions in a single clock cycle.
Dynamic instruction scheduling: The processor dynamically schedules instructions to execute out of order, using a buffer to hold instructions that are waiting for their operands to be available. This allows the processor to execute instructions as soon as their operands are available, rather than waiting for the previous instruction to complete.
Speculative execution: The processor executes instructions before it is known whether they are actually needed. This allows the processor to execute instructions in parallel, but requires additional logic to handle cases where the speculation was incorrect.
In all these cases, a single pipeline is used, but the processor is able to execute multiple instructions concurrently, making it superscalar.

However, it's worth noting that some superscalar processors do use multiple pipelines, known as multi-issue pipelines. In a multi-issue pipeline, the processor has multiple pipelines that can execute instructions independently, allowing for even higher levels of parallelism. But this is not a requirement for a superscalar pipeline.

超标量流水线不一定需要多条流水线吗？

不，超标量流水线不一定需要多条流水线。实际上，超标量流水线可以使用单个流水线和多个执行单元来实现。

在超标量流水线中，处理器可以在单个时钟周期内执行多条指令。这是通过拥有多个执行单元，如算术逻辑单元（ALU）、加载/存储单元和分支单元，来实现的，这些单元可以并发操作。

有几种方式可以实现超标量流水线：

多个执行单元：单个流水线具有多个执行单元，每个单元可以执行不同的指令。例如，处理器可能具有两个ALU、两个加载/存储单元和一个分支单元，从而允许在单个时钟周期内执行多达三条指令。
动态指令调度：处理器动态地调度指令，以便在指令的操作数可用时执行指令。这允许处理器在指令的操作数可用时执行指令，而不需要等待前一条指令完成。
推测执行：处理器在不知道指令是否真正需要时执行指令。这允许处理器并行执行指令，但需要额外的逻辑来处理推测错误的情况。
在所有这些情况下，使用单个流水线，但处理器可以并发执行多条指令，使其成为超标量的。

然而，值得注意的是，一些超标量处理器确实使用多条流水线，称为 多发射流水线。在多发射流水线中，处理器具有多个流水线，可以独立执行指令，从而允许更高水平的并行性。但这不是超标量流水线的要求。

请证明三阶魔方所有的状态构成一个群？

A classic question! 😊

To prove that the set of all possible permutations of a 3x3x3 Rubik's Cube is a group, we need to show that it satisfies the four group axioms:

Closure: The result of combining any two cube permutations is always another cube permutation.
Associativity: The order in which we combine cube permutations does not affect the result.
Identity: There exists an identity permutation that leaves the cube unchanged when combined with any other permutation.
Inverse: For each permutation, there exists another permutation that, when combined, returns the cube to its original state.
Let's go through each axiom:

1. Closure: Given two cube permutations, $a$ and $b$, we can combine them by applying $a$ first, followed by $b$. The resulting permutation is still a valid cube permutation, since each face of the cube is still a 3x3 matrix of colors. Therefore, the set of cube permutations is closed under combination.

2. Associativity: Let $a, b, c$ be three cube permutations. We need to show that $(ab)c = a(bc)$. This means that we can apply the permutations in any order, and the result will be the same. To see why this is true, imagine applying the permutations one by one:

Apply $a$ to the cube, resulting in a new cube state.
Apply $b$ to the resulting cube state, resulting in another new cube state.
Apply $c$ to the resulting cube state, resulting in the final cube state.
Now, let's reorder the operations:

Apply $b$ to the original cube state, resulting in a new cube state.
Apply $c$ to the resulting cube state, resulting in another new cube state.
Apply $a$ to the resulting cube state, resulting in the final cube state.
Since the cube has a finite number of states, there must be a unique final state for each sequence of operations. Therefore, $(ab)c = a(bc)$, and the set of cube permutations is associative.

3. Identity: The identity permutation, often denoted as $e$, is the permutation that leaves the cube unchanged. This is the "do nothing" operation, where each face of the cube remains in its original state. Clearly, combining any permutation with the identity permutation does not change the result, so $e$ satisfies the identity axiom.

4. Inverse: For each permutation $a$, we need to find another permutation $a^{-1}$ such that $a a^{-1} = e$. In other words, we need to find a permutation that "reverses" the effect of $a$. This is possible because the Rubik's Cube has a finite number of states, and each permutation is a bijection (a one-to-one correspondence) between these states.

To find the inverse of a permutation, we can simply apply the permutation and then "undo" each step in reverse order. For example, if $a$ is a permutation that rotates the top face clockwise, its inverse $a^{-1}$ would be a permutation that rotates the top face counter-clockwise.

Since we have shown that the set of cube permutations satisfies all four group axioms, we can conclude that it forms a group, often denoted as $G$. This group is known as the Rubik's Cube group or the Cube group.

The Rubik's Cube group has some fascinating properties, such as:

It is a finite group, with exactly 43,252,003,274,489,856,000 elements.
It is a non-Abelian group, meaning that the order of operations matters.
It has a rich structure, with many subgroups and conjugacy classes.
The study of the Rubik's Cube group has led to important advances in group theory, combinatorics, and computer science.

一个经典的问题！😊

要证明三阶魔方的所有可能排列是一个群，我们需要展示它满足四个群公理：

封闭性：任意两个魔方排列的组合结果总是一个魔方排列。
结合律：魔方排列的组合顺序不影响结果。
单位元：存在一个单位排列，使得它与任何其他排列组合时保持魔方不变。
逆元：对于每个排列，存在另一个排列，使得它们组合时返回魔方的原始状态。
让我们逐一证明每个公理：

1. 封闭性： 给定两个魔方排列，$a$ 和 $b$，我们可以通过先应用 $a$，然后应用 $b$ 来组合它们。结果排列仍然是一个有效的魔方排列，因为每个面都是一个 3x3 的颜色矩阵。因此，魔方排列的集合在组合下是封闭的。

2. 结合律： 让 $a, b, c$ 是三个魔方排列。我们需要证明 $(ab)c = a(bc)$。这意味着我们可以以任何顺序应用排列，而结果将相同。要看到这是为什么正确的，想象应用这些排列一个一个：

应用 $a$ 到魔方，结果是一个新的魔方状态。
应用 $b$ 到结果魔方状态，结果是一个新的魔方状态。
应用 $c$ 到结果魔方状态，结果是最终的魔方状态。
现在，让我们重新排序操作：

应用 $b$ 到原始魔方状态，结果是一个新的魔方状态。
应用 $c$ 到结果魔方状态，结果是一个新的魔方状态。
应用 $a$ 到结果魔方状态，结果是最终的魔方状态。
由于魔方有有限数量的状态，因此每个操作序列都必须有一个唯一的最终状态。因此，$(ab)c = a(bc)$，魔方排列的集合是结合的。

3. 单位元： 单位排列，通常表示为 $e$，是保持魔方不变的排列。这是“什么都不做”的操作，其中每个面保持原始状态。明显地，将任何排列与单位排列组合不会改变结果，因此 $e$ 满足单位元公理。

4. 逆元： 对于每个排列 $a$，我们需要找到另一个排列 $a^{-1}$，使得 $a a^{-1} = e$。换言之，我们需要找到一个排列来“撤销”$a$ 的效果。这是可能的，因为魔方有有限数量的状态，每个排列都是这些状态之间的一对一对应。

要找到排列的逆元，我们可以简单地应用排列，然后以相反的顺序“撤销”每个步骤。例如，如果 $a$ 是一个将顶面顺时针旋转的排列，那么它的逆元 $a^{-1}$ 将是将顶面逆时针旋转的排列。

由于我们已经展示了魔方排列的集合满足所有四个群公理，因此我们可以结论说它是一个群，通常表示为 $G$。这个群称为 Rubik's Cube 群 或 魔方群。

魔方群有一些有趣的性质，例如：

它是一个有限群，恰好有 43,252,003,274,489,856,000 个元素。
它是一个非阿贝尔群，意味着操作顺序很重要。
它有一个丰富的结构，具有许多子群和共轭类。
魔方群的研究已经导致了群论、组合数学和计算机科学等领域的重要进展。

Linux 操作系统的设计中是否存在数学中的群结构呢？

Linux 操作系统的设计中是否存在数学中的群结构呢？

虽然 Linux 内核并不是明确地基于数学群结构设计的，但是有一些实例中数学群理论概念被使用或类似于某些设计元素。以下是一些例子：

1. 进程组和会话：在 Linux 中，进程可以被分组到进程组和会话中。进程组是一组可以作为单个单位来操作的进程，例如向组中的所有成员发送信号。这个概念类似于数学中的群概念，其中一个集合在二元运算下闭合（例如信号发送）。然而，这只是一个松散的类比，Linux 进程组机制并不是数学群结构的直接实现。

2. 文件系统权限：Linux 文件系统权限可以被视为群作用，其中一个用户组（例如 Unix 组）作用于文件系统对象的集合。权限位（例如读、写、执行）可以被视为二元运算，它将组的身份与文件系统对象的身份组合。虽然这不是数学群理论的直接应用，但是这个机制与群作用概念共享一些相似之处。

3. Linux 内核数据结构中的对称性：一些 Linux 内核数据结构，例如 inode 缓存或页面缓存，展示出类似于群结构的对称性。例如，inode 缓存可以被视为等价类的集合，其中每个类代表具有相似属性的一组 inode。这个对称性可以被利用来优化缓存管理并减少缓存miss的数量。虽然这不是数学群理论的直接应用，但是这个例子说明了数学概念如何激发高效的数据结构设计。

4. 密码学算法：Linux 使用各种密码学算法，例如 AES 和 RSA，这些算法严重依赖数学群结构。例如，RSA 算法基于大合数的难以因式分解，这与有限群概念紧密相关。虽然这不是 Linux 内核中数学群理论的直接应用，但是这些密码学算法是 Linux 安全基础设施的essential组件。

总之，虽然 Linux 操作系统的设计中没有明确、直接的数学群结构应用，但是有一些实例中数学群理论概念被使用或类似于某些设计元素。这些例子说明了数学概念对复杂系统设计的微妙却重要的影响。

对称加密构成群么？ 符合不符合四个群公理？

对称加密构成群么？ 符合不符合四个群公理？

对称加密是否构成群？

在对称加密中，我们有一个明文集、一个密钥集和一个加密函数，该函数将明文和密钥作为输入并生成密文。让我们将明文集记为 P，密钥集记为 K，加密函数记为 E。

要构成群，我们需要在明文集或密钥集上定义一个二元运算。一个可能的运算是加密函数的组合。具体来说，让我们定义运算如下：

对于两个密钥 k1, k2 ∈ K，定义运算为：k1 ∘ k2 = E(E(p, k1), k2) 对于某个明文 p ∈ P。
这个运算是结合的，即(k1 ∘ k2) ∘ k3 = k1 ∘ (k2 ∘ k3) 对于所有 k1, k2, k3 ∈ K。

然而，这个运算没有单位元，也没有逆元。具体来说：

没有密钥 e ∈ K，使得 k ∘ e = k 对于所有 k ∈ K。
对于每个密钥 k ∈ K，没有密钥 k' ∈ K，使得 k ∘ k' = e，其中 e 是某个单位元。
因此，对称加密不构成传统意义上的群。

对称加密方案是否满足四个群公理？

让我们检查四个群公理，看看对称加密方案是否满足它们：

闭包：对于所有 k1, k2 ∈ K，k1 ∘ k2 ∈ K。（满足）
结合：对于所有 k1, k2, k3 ∈ K，(k1 ∘ k2) ∘ k3 = k1 ∘ (k2 ∘ k3)。（满足）
单位元：存在元素 e ∈ K，使得对于所有 k ∈ K，k ∘ e = k。（不满足）
逆元：对于每个元素 k ∈ K，存在元素 k' ∈ K，使得 k ∘ k' = e，其中 e 是单位元。（不满足）
如我们所见，对称加密方案只满足闭包和结合公理，但不满足单位元和逆元公理。因此，它们不构成传统意义上的群。

然而，值得注意的是，一些对称加密方案，例如高级加密标准（AES），在考虑密钥集和加密函数时具有群似结构。例如，AES 具有“密钥敏捷性”属性，即使用一个密钥加密明文，然后使用另一个密钥加密结果等同于使用从两个原始密钥派生的单个密钥加密明文。这个属性可以被视为群似结构，但它不是传统意义上的群。

长方形对称群是克莱因四元群吗？

为什么因式分解多项式，要让多项式等于0求根，能保证分解后的结果在其他值也和原多项式相等吗?

多项式是一组线性无关的基通过有限次加减乘除形成的，因为线性无关，所以如果两个同阶多项式在足够多的点 （ 大于等于阶次）处相等，那么它们必须是相同的多项式。

The reason why we can factor a polynomial and then set it equal to 0 to find the roots, and still guarantee that the factored form is equivalent to the original polynomial for all values, lies in the fundamental theorem of algebra.

Fundamental Theorem of Algebra: Every non-constant polynomial with complex coefficients has at least one complex root.

This theorem implies that every polynomial of degree $n$ can be written in the form:

$$p(x) = a_n(x - r_1)(x - r_2) \cdots (x - r_n)$$

where $a_n$ is the leading coefficient, and $r_1, r_2, \ldots, r_n$ are the roots of the polynomial.

Why factoring works: When we factor a polynomial, we are essentially finding the roots of the polynomial and rewriting it in the form above. Since the polynomial is equal to 0 when $x = r_i$ for any root $r_i$, we can write:

$$p(x) = a_n(x - r_1)(x - r_2) \cdots (x - r_n) = 0$$

for all values of $x$ that satisfy the equation.

Here's the crucial part: since the polynomial is equal to 0 when $x = r_i$, we can conclude that the factored form is equivalent to the original polynomial for all values of $x$. This is because the factored form is simply a rearrangement of the original polynomial, using the roots as factors.

Why it works for all values, not just the roots: The key insight is that the factored form is not just equal to 0 at the roots, but it is also equal to the original polynomial for all values of $x$. This is because the factored form is a polynomial expression, and polynomial expressions are continuous functions.

In other words, if two polynomial expressions are equal at a set of points (in this case, the roots), they must be equal everywhere. This is known as the Identity Theorem for Polynomials, which states that if two polynomials are equal at a set of points, they must be identical.

So, when we factor a polynomial and set it equal to 0 to find the roots, we can be sure that the factored form is equivalent to the original polynomial for all values of $x$, not just the roots.

I hope this helps clarify things! 😊

多项式因式分解的原因是，为什么我们可以将多项式分解，然后将其设置为 0 来找到根，并且仍然保证分解后的结果在其他值也与原多项式相等， lies in the 根本定理 of algebra。

根本定理 of Algebra： 每个非常数多项式具有至少一个复根。

这个定理意味着，每个度数为 $n$ 的多项式可以写成以下形式：

$$p(x) = a_n(x - r_1)(x - r_2) \cdots (x - r_n)$$

其中 $a_n$ 是首项系数，$r_1, r_2, \ldots, r_n$ 是多项式的根。

为什么因式分解 works： 当我们对多项式进行因式分解时，我们实际上是找到多项式的根，并将其重写为上述形式。由于多项式在 $x = r_i$ 时等于 0，我们可以写：

$$p(x) = a_n(x - r_1)(x - r_2) \cdots (x - r_n) = 0$$

对于所有满足方程的 $x$ 值。

这里的关键部分是：由于多项式在 $x = r_i$ 时等于 0，我们可以断言，分解后的形式对于所有 $x$ 值都是等同于原多项式的。这是因为分解后的形式只是原多项式的一种重排，使用根作为因子。

为什么它适用于所有值，而不仅仅是根： 关键的见解是，分解后的形式不仅仅在根处等于 0，还等同于原多项式对于所有 $x$ 值。这是因为分解后的形式是一个多项式表达式，而多项式表达式是连续函数。

换言之，如果两个多项式表达式在一组点（在这里是根）处相等，那么它们必须在所有地方相等。这被称为多项式的 同一性定理，它声称，如果两个多项式在一组点处相等，那么它们必须是相同的。

因此，当我们对多项式进行因式分解，并将其设置为 0 来找到根时，我们可以确保，分解后的形式对于所有 $x$ 值都是等同于原多项式的，不仅仅是根。

希望这能够帮助澄清事情！ 😊

如果两个多项式表达式在一组点（在这里是根）处相等，那么它们必须在所有地方相等。这被称为多项式的 同一性定理，它声称，如果两个多项式在一组点处相等，那么它们必须是相同的,对吗？

I think I made a mistake there. 🙈

The statement "如果两个多项式表达式在一组点（在这里是根）处相等，那么它们必须在所有地方相等" is not entirely accurate.

The correct statement is:

Identity Theorem for Polynomials: If two polynomials are equal at a sufficient number of points, then they must be identical.

In other words, if two polynomials $p(x)$ and $q(x)$ are equal at $n+1$ distinct points, where $n$ is the degree of the polynomials, then they must be identical.

This theorem does not require the points to be roots of the polynomial. Any set of $n+1$ distinct points will do.

So, to correct my previous statement:

如果两个多项式在足够多的点处相等（不一定是根），那么它们必须是相同的。

Thank you for pointing out the mistake! 😊

I think I made a mistake there. 🙈

_statement "如果两个多项式表达式在一组点（在这里是根）处相等，那么它们必须在所有地方相等" 并不完全准确。

正确的陈述是：

多项式同一性定理： 如果两个多项式在足够多的点处相等，那么它们必须是相同的。

换言之，如果两个多项式 $p(x)$ 和 $q(x)$ 在 $n+1$ 个不同的点处相等，其中 $n$ 是多项式的度数，那么它们必须是相同的。

这个定理并不要求这些点是多项式的根。任何一组 $n+1$ 个不同的点都可以。

所以，为了纠正我的前一个陈述：

如果两个多项式在足够多的点处相等（不一定是根），那么它们必须是相同的。

谢谢你指出我的错误！ 😊

相同的点不一定是根，可以是任意位置的值，比如对于两个n阶多项式：

,它们在处相等。

则构造F(x) = f(x)-g(x),假如f(x)==g(x)，则已证明 ，假如f(x)!=g(x),则是F(x) = 0的n个根，所以两个多项式任意位置的相等问题转换成了根的问题，所以这个“任意点”可以不是根点。

被deepseek惊艳了一下：

什么是基本对称多项式

二次函数的复共扼闭域是什么？

---

End