计算机图形学-3D图像基础

计算机图形学第一定律：

如果它看起来正确，那就是对的。

图形学对数的理解

自然数和整数研究称为离散数学，而对实数的研究则称为连续数学，实数是一种精致的虚构，它是一种无害的妄想，就连宇宙都不是连续的，宇宙不仅是离散的，而且还是有限的。某种程度上，可能存在一种远超人类的外星文明，它们没有连续数学，微积分，也没有无限的概念。计算机世界不就是这样一个世界么？

三角函数恒等式

与对称性相关的基本恒等式：

毕达哥拉斯定理：

毕达哥拉斯恒等式：

和或差恒等式：

等腰三角形恒等式

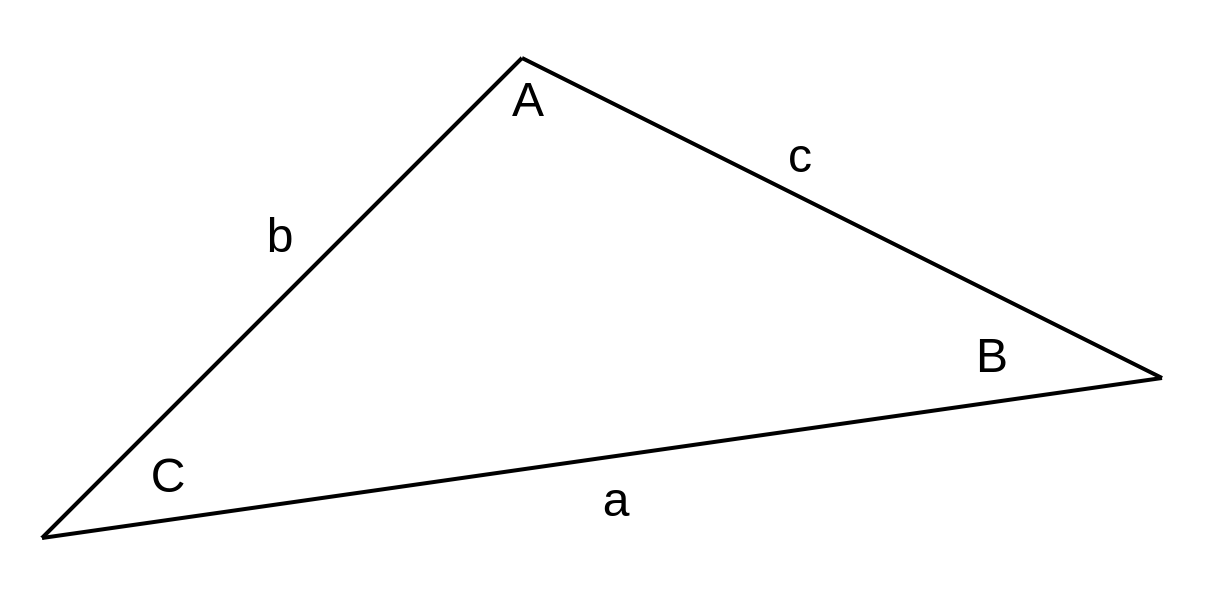
正弦定理：

余弦定理：

剪切变换

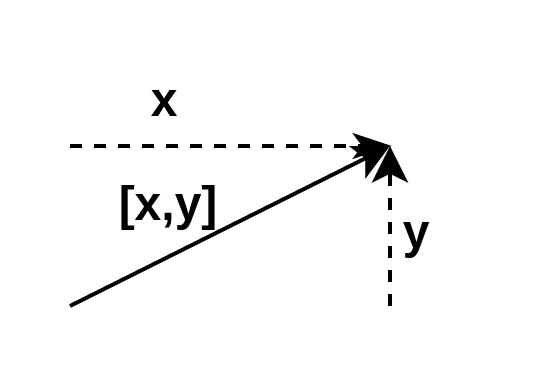
矢量：

矢量没有位置，只有大小和方向，这可能听起来不可能，但我们每天处理的许多数量都有规模和方向，但没有位置。因为矢量用于表示事物之间的位移和相对差异，所以它们可以描述相对位置。

当使用笛卡尔坐标来描述矢量时，每个坐标将度量相应维度中的有符号位移，例如，在二维中，可以列出平行于X轴的位移，和平行于Y轴的位移。

0矢量是唯一一个大小为0，且没有方向的矢量，但它不是点，因为点是有位置的，矢量没有位置，即便是0矢量也是如此。

位置：

宇宙中绝对位置并不重要，你知道你现在处于宇宙中哪个确切位置吗？你不知道，没关系，没有人知道，也不需要知道，所有位置都是相对的，包括速度，音量，温度等等，这些量都可能会出现负数，仅仅意味着它比你选定的标准更低。

点和矢量的关系

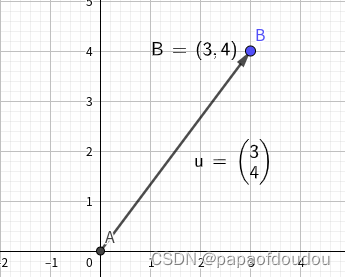
既然位置是相对的，点也是相对的，矢量[x,y]给出了从原点到(x,y)的位移。

点积：

点积的几何定义不假设任何特定坐标系或甚至不假定使用笛卡尔坐标系。

一个向量的对偶，就是把该向量当成矩阵所定义的线性变换，一个多维空间到一维空间的线性变换的对偶，就是多维空间中的某个特定向量，所以，一个二维向量的对偶，就是将二维向量横放组成的矩阵（实际上也是行向量）对应的线性变换。

为什么需要多个坐标空间？

任何一个三维坐标系可以无限延展，包含了空间中所有的点，这个坐标系为世界坐标空间，为何还需要其它坐标空间？答案是某些信息仅在特定坐标系下才有意义。像每个城市都需要有自己的地图。

持续补充。。。