数学女孩-伽罗瓦理论读书笔记尺规作图

和干巴巴的数学课本给人的印象不同，真实的数学史远远比金庸的武侠小说来的精彩，这本书的主角伽罗瓦，就是这样一位站在天赋领域顶点的悲情数学家，论天赋，伽罗瓦应该是罕有敌手了，人类思维纬度的提升带来的后果有多么可怕，其他人都是硬啃难题，伽罗瓦在16岁就开启了上帝视角，19岁之前创建群论，仅仅是利用该理论的推论，就足以KO古希腊三大作图难题中的两道，群论的入门定理还给出了五次方程求根公式的的充要条件。这还没完，后世对群论的研究还开创了近世代数，把数学研究带入了全新领域。21岁为情赋死。生前成果不被承认，死后多年计算手稿阿才被刘维尔发现并整理出来，一经发表，镇惊四座，人们才知道地球上曾经有这样一位绝世天才出现过。这是一位悲情到让人心疼的数学家，一位凭一己之力推动人类文明进程前进的悲剧英雄，一位永远活在21岁的孤独的天才.

伽罗瓦的天赋在数学史上是独一档的存在，他短暂一生的灵光闪现展现出来的卓越智慧即使强大如高斯，欧拉也有不及。

决斗前夜，伽罗瓦将他的部分研究成果写下来，在他的临终手稿中有这么一段文字：

我期待有人能解开我在这里书写的潦草又难以理解的一切，并让它进一步发展.

                                                                                                                      ------埃瓦里斯特.伽罗瓦

伽罗瓦有能力证明旷世难题，却无法证明自己，他把对自己的证明留给了后人。在去世十四年后，这个人终于出现了，它叫刘维尔，比伽罗瓦大两岁，也是一位数学家。

数学是理性的，但是创立群论的伽罗瓦却感性的让人心疼，啥都别说了，一起膜拜吧：

这里主要对这本书的尺规作图部做一个学习记录，以免忘记。

尺规作图的定义

尺规作图是用圆规和没有刻度的直尺在有限的步骤中作出平面图形。

尺规作图的原则

首先明确直尺和圆规可以做的事情，这是规则。

直尺能够办到的事只有一件，即画出通过给定2点的直线，这两个点不能重合，也不能使用直尺上的刻度，不可以测量两点间的距离，总之，这把直尺能做的只有帮助我们画出通过给定2点的直线，并且点需要事先存在。

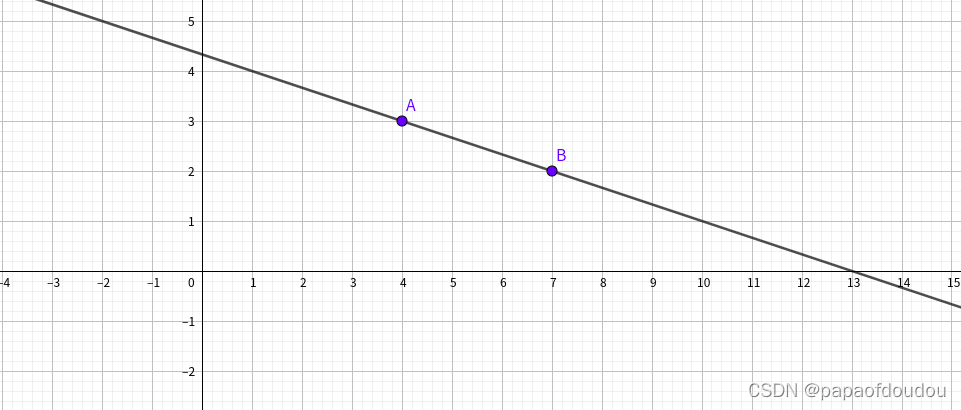
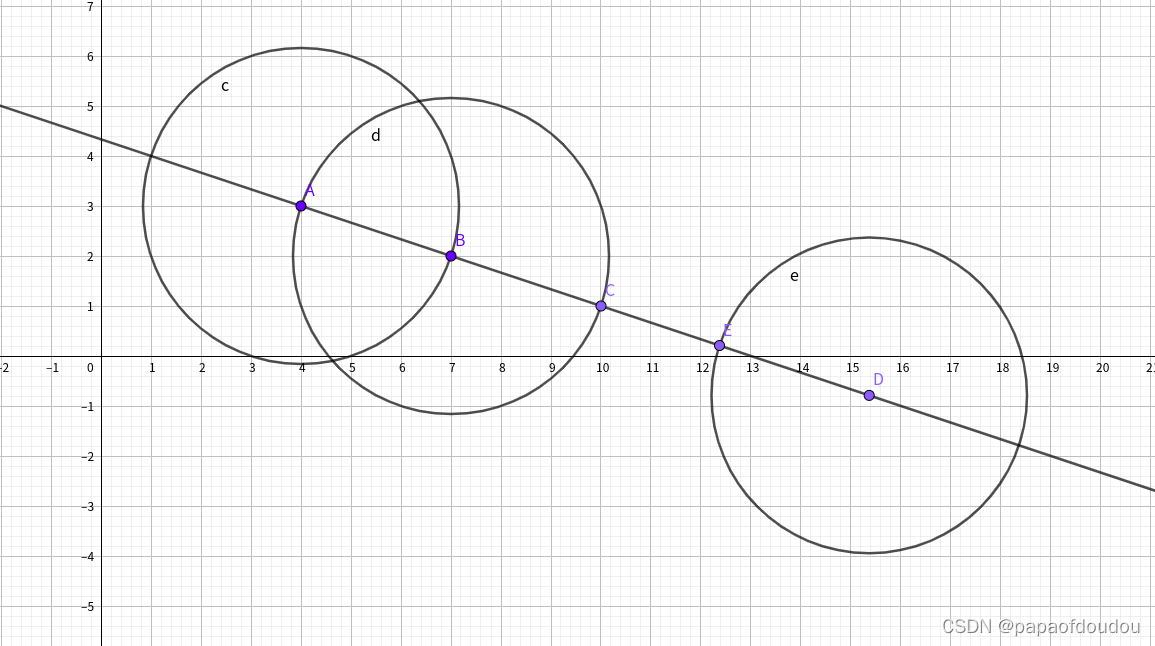
接着是圆规，圆规是画圆的工具，使用圆规可以办到的事情也只有一件，即以给定的2个点的其中一点为中心，画出通过另一个点的圆，用圆规画完的圆，也可以将圆规带有针的一端移到其它点上，以另一个点为半径画出另一个半径相同的圆。

可见无论圆规还是直尺，必须由两个可作点，最初始的两个可作点是单位长度1的两个端点。

做图必须是精确的，这是古希腊理想化的几何形式所设定的苛刻条件，在这样的理想体系中，直线没有宽度，点没有大小，能够作图的图形，意味着不只是小数点的近似，后十位，后百位或者后十亿位的数字彼此相等，而是到无限位的数字都相等。

正因为如此，我们假设可以把圆规的一脚无限精确的放置在任何一个已经给出的，或者之后会被做图做出来的点上，可以让圆规的半径无限精确地等于任意两点间的距离，也可以画一条无限精确地穿过两点的直线。

通过这些规则我们可以看到，作图的前提是需要有两个点，如果不满足，就什么也做不出来。我们必须假定一开始会给定2点，并且后面绘制产生的点也只能是直线和直线，圆和圆，以及直线与圆的交点。

一句话，点具有精确的吸附能力，它可以将直尺（直线）吸附到自己身上毫无误差，也可以将圆规的两个脚吸附过去没有丝毫误差。

可作数：两个可作点之间的距离，以及该距离的负值，称为可作数。

规则说清楚了，接下来看在规则之内，尺规作图能作出哪些数。

所有的整数

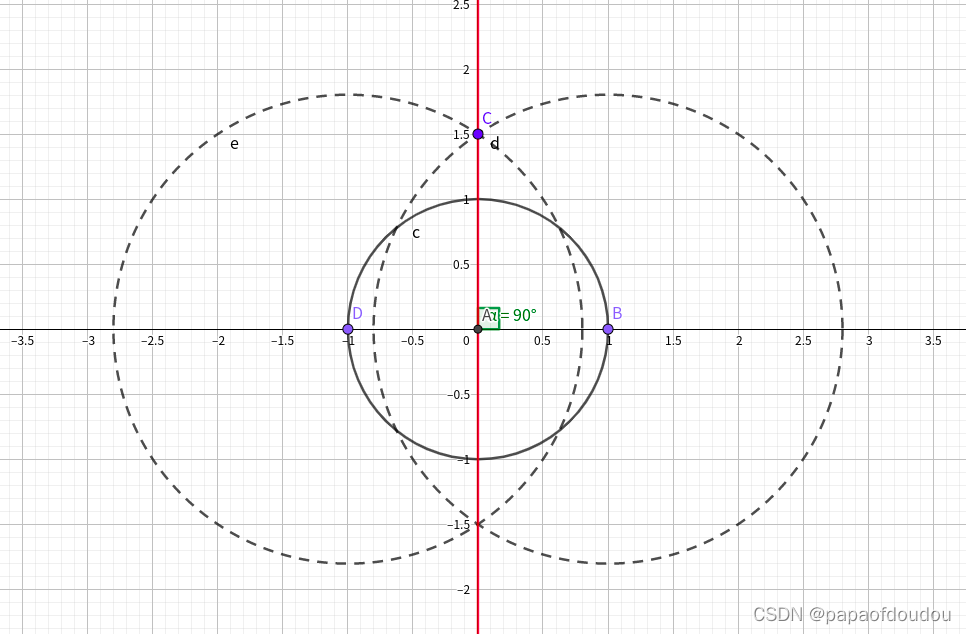
通过圆规，不断的将单位1的线段复刻在数轴上，可以画出所有的整数刻度，我们一步步来实现，首先实现基本的，画垂线, 做完垂线后，坐标轴就出来了。

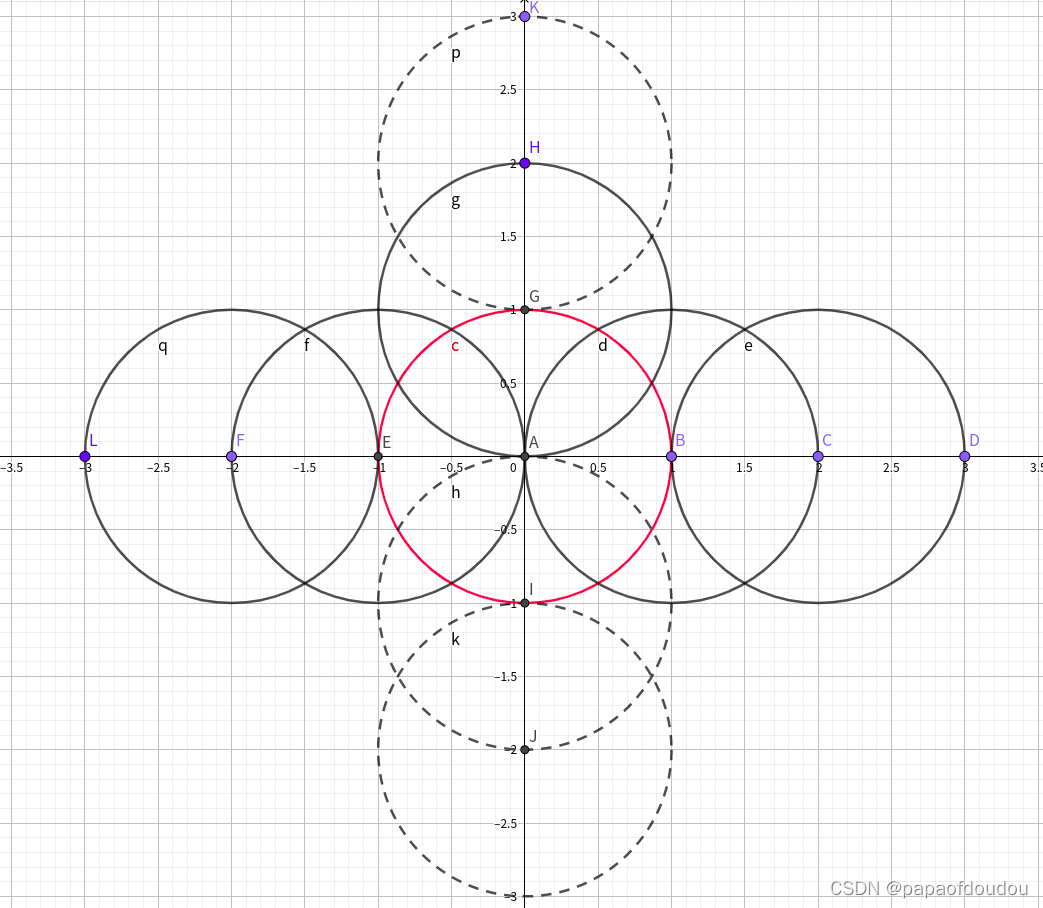
 在垂线上做整数，可以作出笛卡尔坐标系：

 画平行线

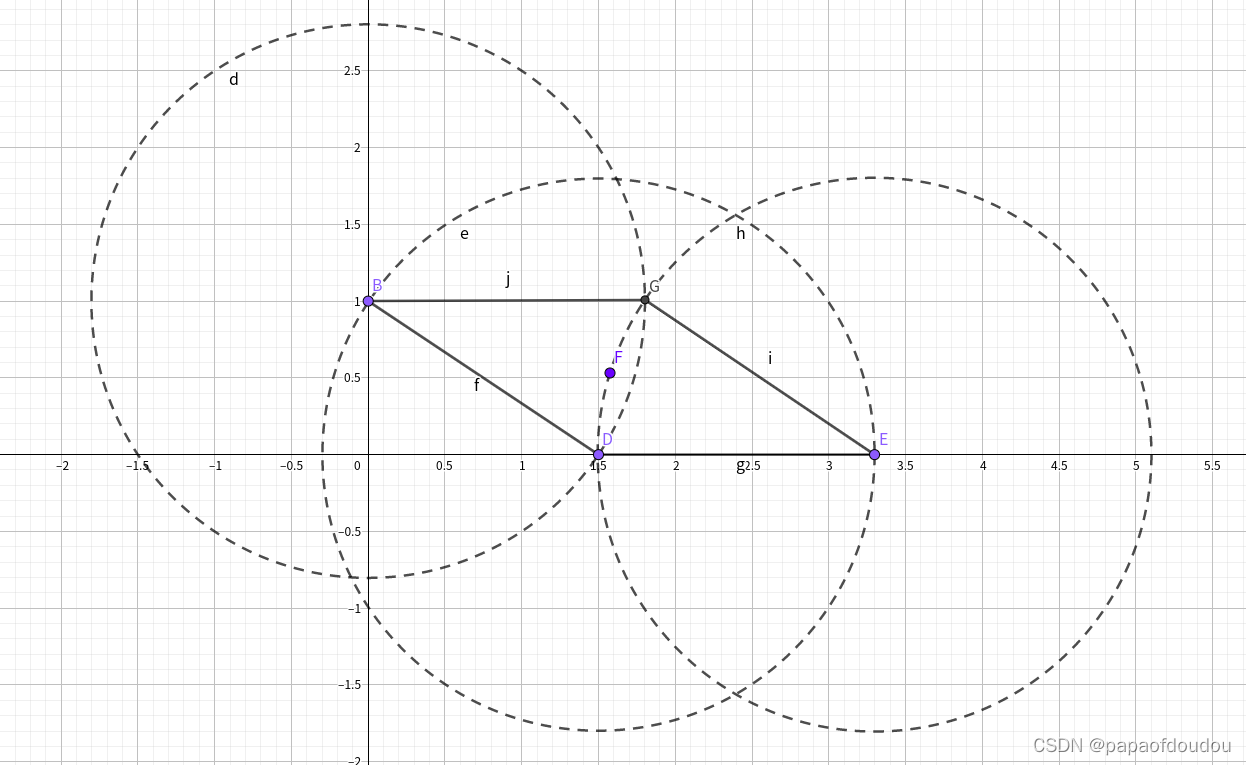
1. 如图，先在直线g外画一点，标明为B。
2. 以点B为圆心——以大于点B到直线g的距离为半径画弧，交直线g于点D。
3. 以点D为圆心，同样长的半径画弧，与直线交于点F。
4. 再以点F为圆心——同样长的半径画弧，与以圆心B画的弧相交，在最上方的相交点标明为G。
5. 用直尺与铅笔，连接点B和点G画直线，这条直线就是平行于G的平行线。

画笛卡尔坐标系

具备了以上技能，我们就可以用尺规画出笛卡尔坐标系下的整数坐标网格了。

到目前为止，所有的整数和整数坐标，以及以此建立的网络上的任意亮点之间的线段表示的距离，都是可以用尺规做出来的。

画分数

接着，根据绘制平行线的方法，所有分数也是可以由尺规做出来的，比如下面五等分CD。只要将线段放到坐标轴上，一端和原点重合，另一端连接X轴上的平分数N，之后做N-2个平行线即可。

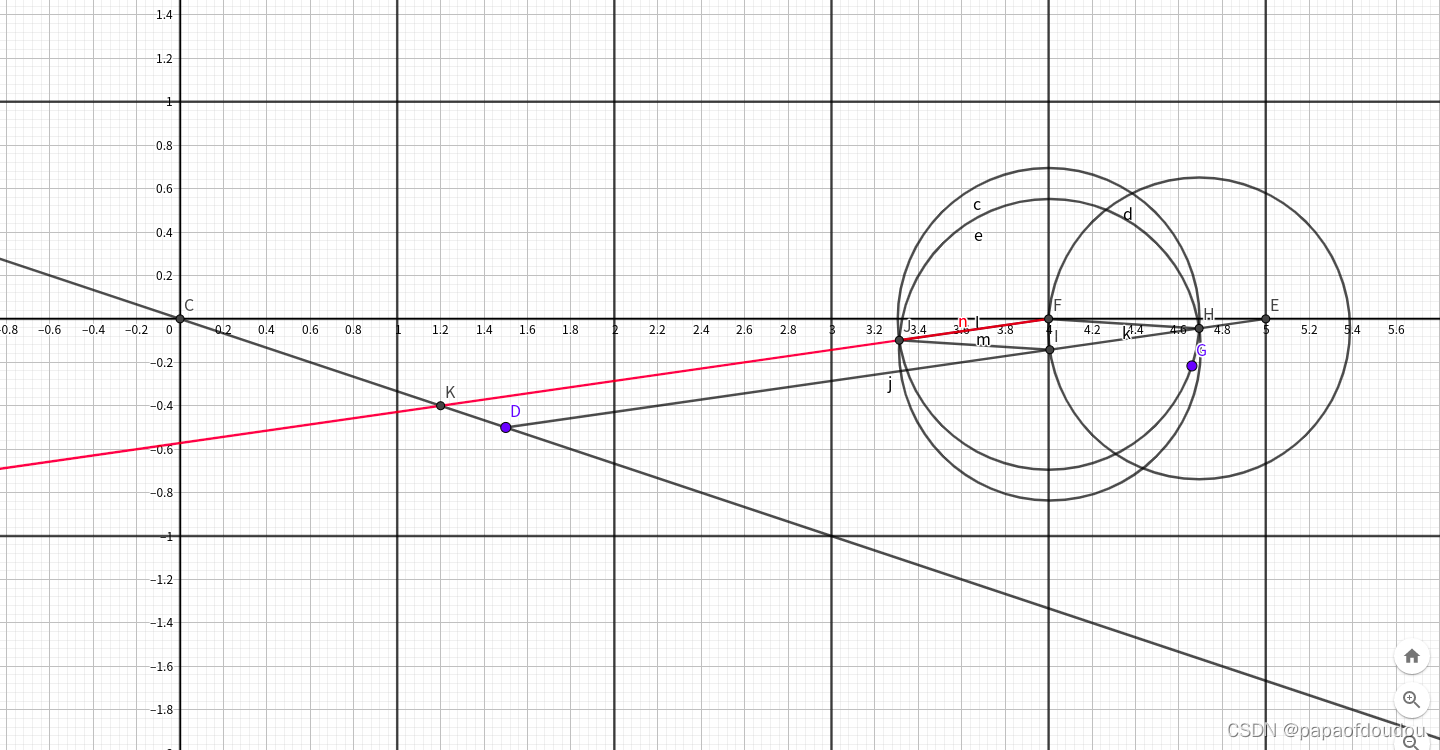
所以，所有整数和分数长度的线段是可以做出来的，也有是说，所有有理数长度的线段都是可以由尺规作图做出来，这样整数的加减乘除也都可以由尺规作图表示。

绘制二次开方数

接下来看， 能否做二次开根号，我们发现，从开始做起，任何整数开根号都可以作出来，如下图，,下图以为0.5为单位1。

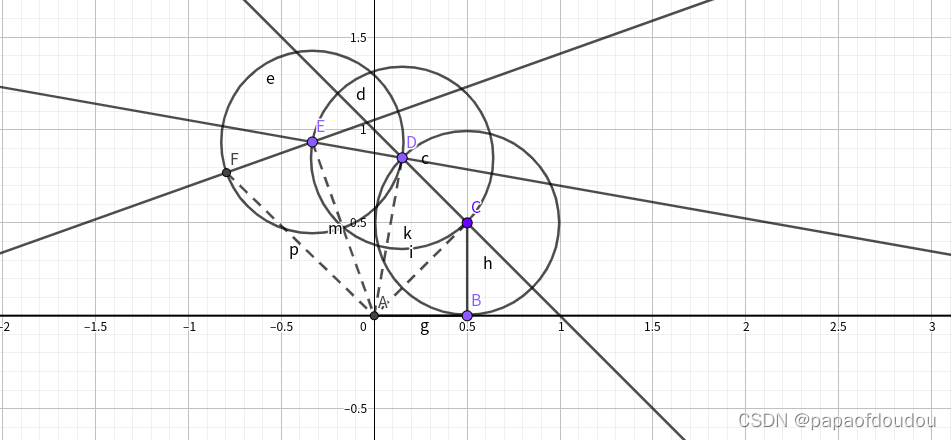
 之后，更进一步，任意有理数开方，也都能通过尺规作图做出来：

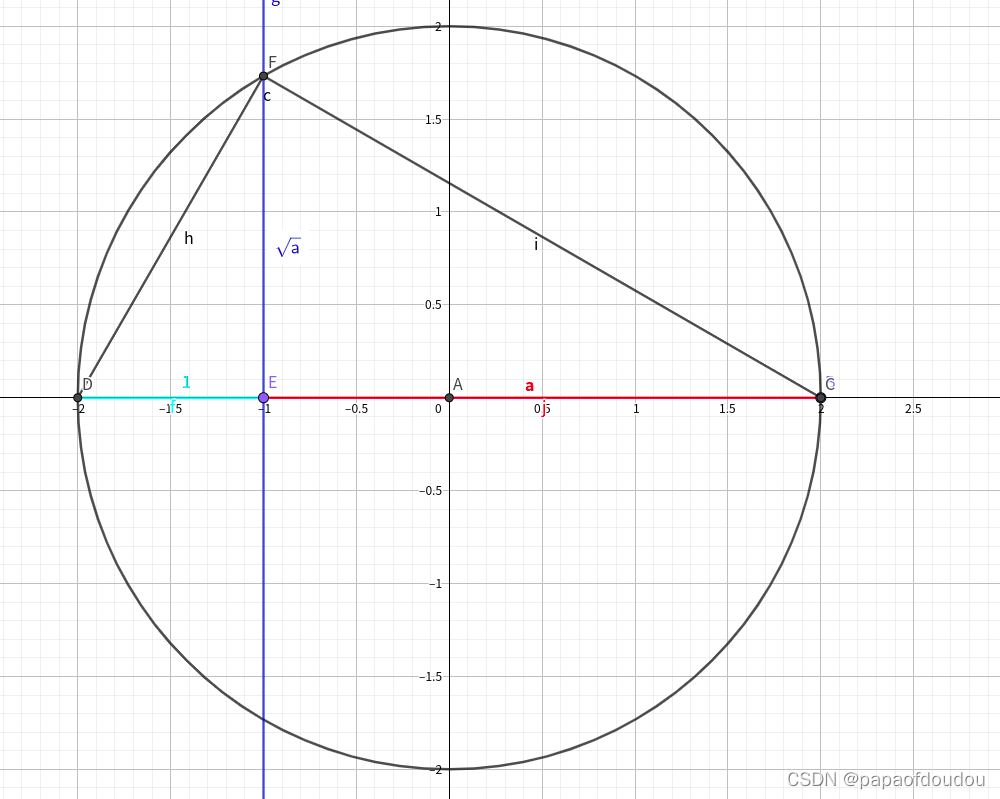
既然对于任意有理数a,b,c,....都可以作出

那么他们的加减乘除以及再次开方，当然可以用同样的方式做出来，换句话说，有限次的有理数开平方，都可以通过尺规作图做出来

等等，都可以通过尺规作图做出来，所有能够用尺规作图做出来的数，叫做规矩数，规矩数是重复进行加减乘除运算与开根号运算能够得出的数。

总结

建立直线与直线，直线与圆，圆与圆的联立方程组，求出交点的坐标，就能理解什么是规矩数了，直线方程是一次式，圆方程是2次式子，不管做的图多么复杂，总归是圆和直线，各类交点的长度，坐标都可以通过解最多不超过2次的方程表示，解这些2次方程，最多当然只能得到开二次方的数，不管多少层开方，总归是有限的二次方开方，都可以做。

说了这么多，最后的结论用通俗的表达就是，能够用尺规作图的长度为K的线段的充分必要条件是，当且仅当K可由1进行加减乘除以及有限次开平方等运算得到。

伽罗瓦对此的即使更加简单和直接，通过直线和圆，只能做2次扩域，无法做到开3次方或者其他高次方。

等学会了伽罗瓦理论，在回过头来看这个问题，会不会超级简单。

实数的分域，规矩数的位置，注意几点：

1. 所有有理数都是规矩数.
2. 规矩数的偶数次方根是规矩数.
3. 规矩数相加，相减，相乘，相除（除数不得为0）的结果为规矩数.
4. 规矩数包括所有的有理数和无理数的一部分。
5. 规矩数一定是代数数（为一整系数代数方程的解），且以此解为其解的最小多项式其次数为2的n次方,但是代数数不一定是规矩数。因为可能有高次方根存在。
6. 超越数，例如pai, e,以及一数对应的最小多项式为三次、五次，此数必定不是规矩数。

7. 代数数是代数与数论中的重要概念，指任何整系数多项式的复根，所有代数数的集合构成一个域，称为代数数域。不是代数数的数称为超越数，例如：圆周率 π、自然对数的底数 e。虽然根号2也是无理数，但我们至少可以这样表述它"平方为2的数",换句话说，我们可以使用整数的算术表达表示根号2所满足的关系数，即它是这样一个数，满足,虽然我们也不知道它的具体值是多少，但我们知道它的性质。

8. 标准的尺规作图步骤的每一步都相当于计算一个次数不超过2的多项式方程，因此能够通过有限步做出的线段长度必然是有限个有理系数多项式迭代后得到的多项式的根，从而是代数数。

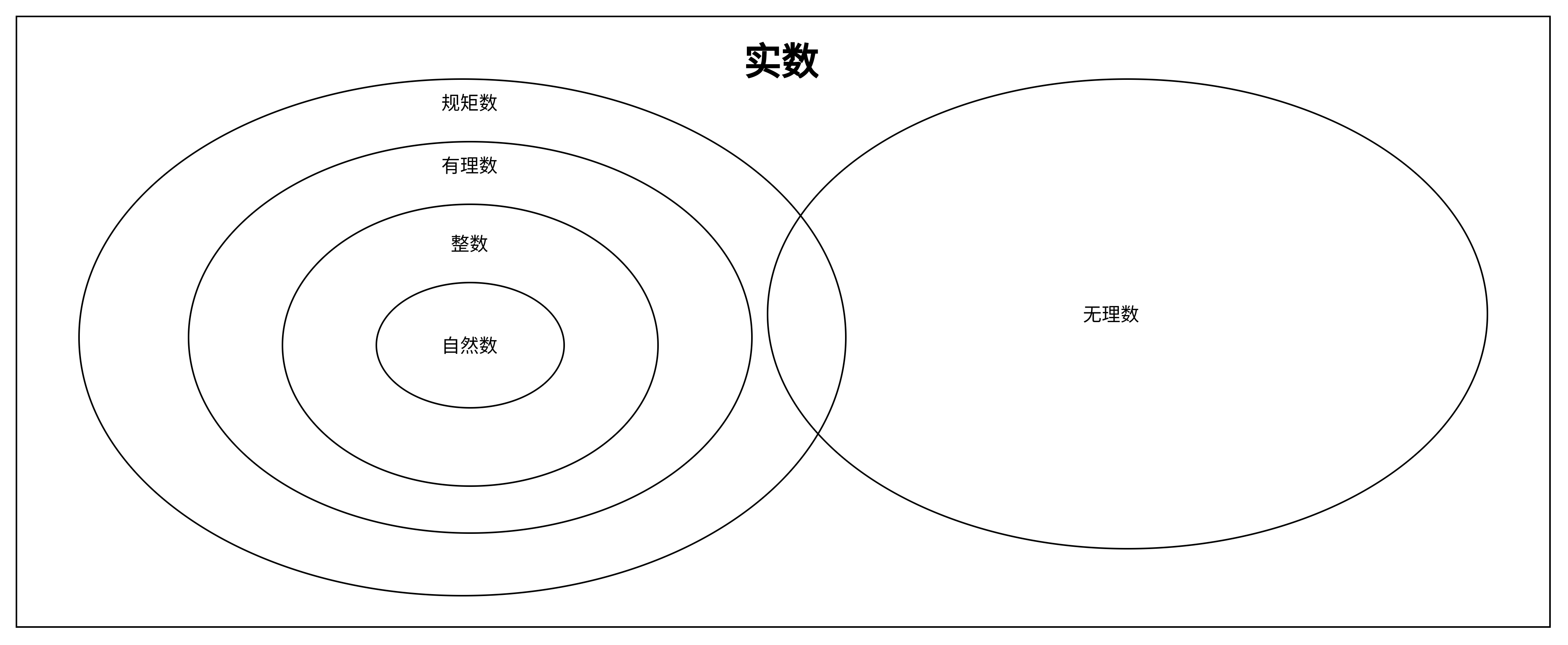
从下图来看，规矩数是虚线围起来的区域包含的部分，包括所有的有理数和一部分无理数，这部分无理数主要是有理数的二次方根构成的扩域。

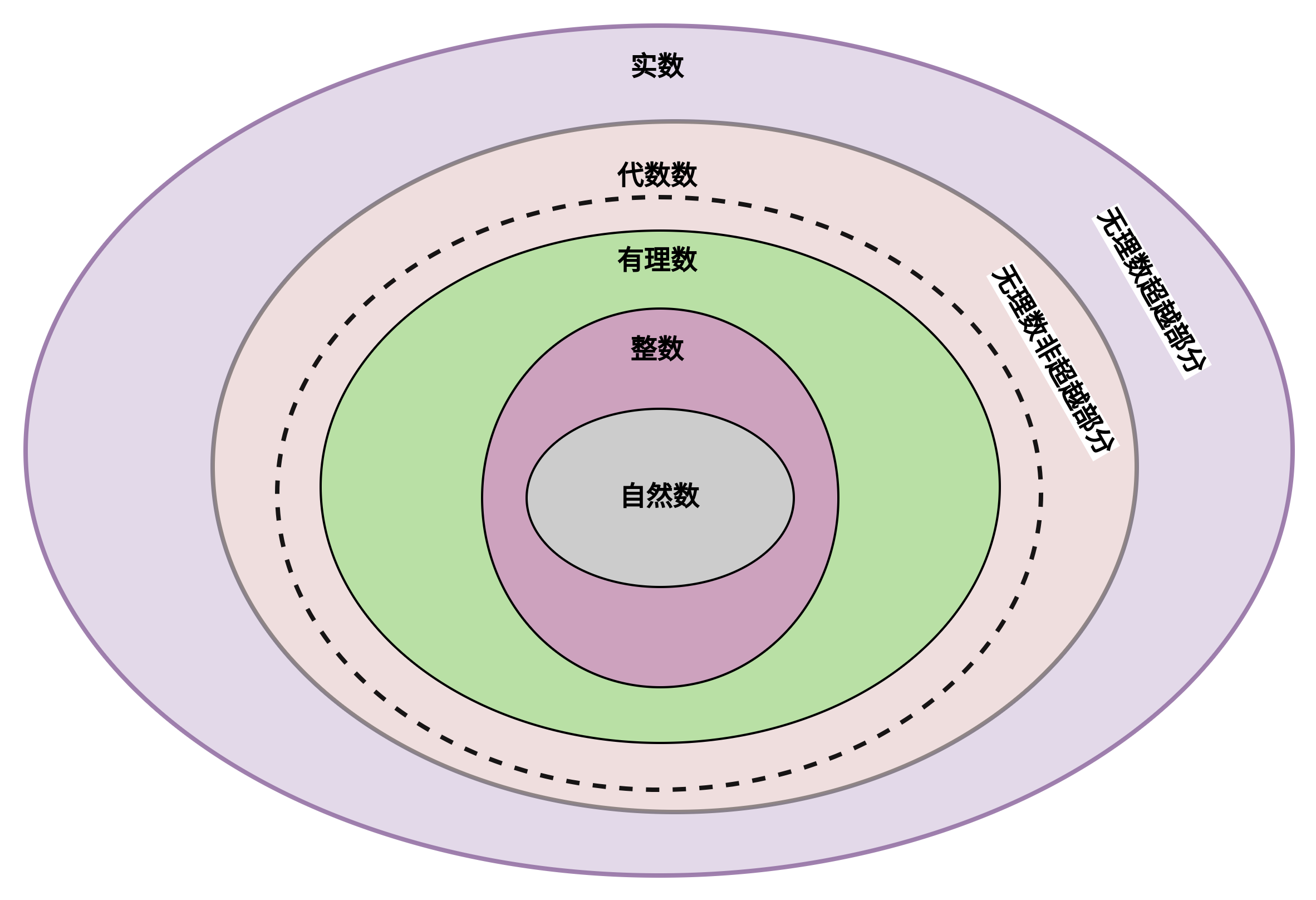
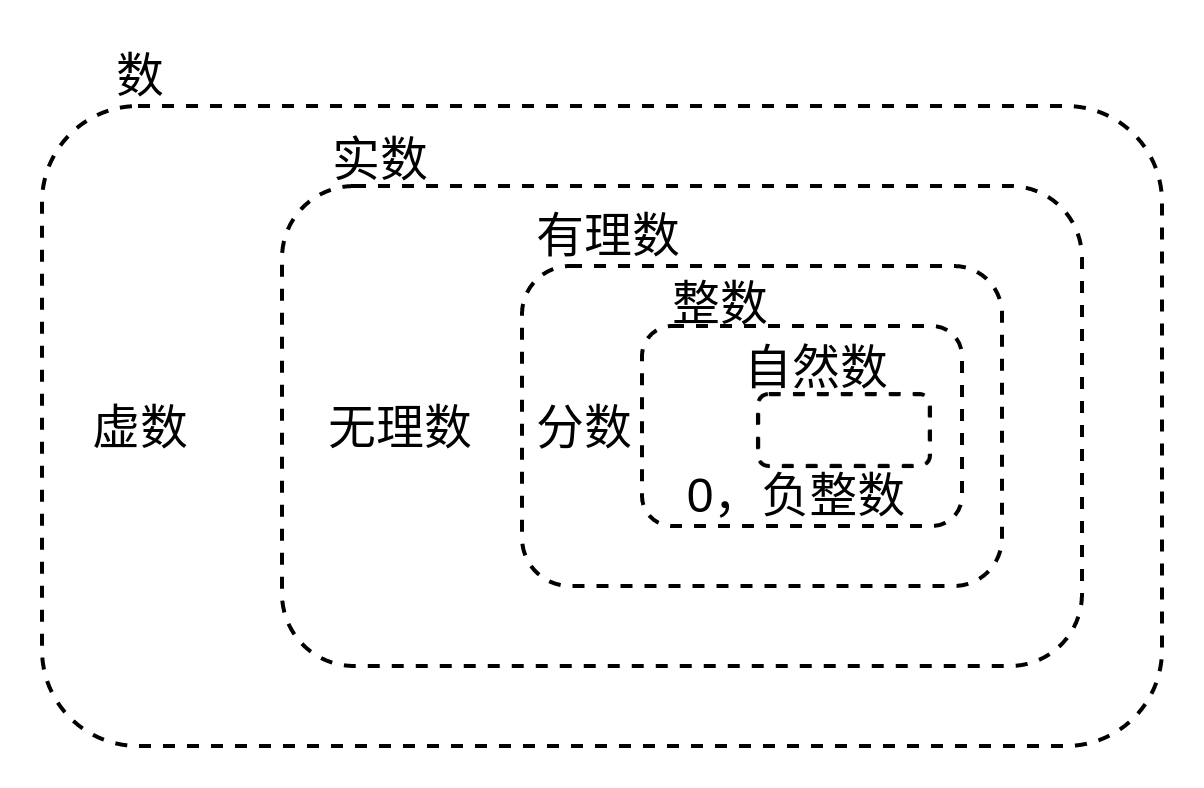
下面这幅图也是有些问题的，有理数和无理数没有覆盖实数的所有情况：

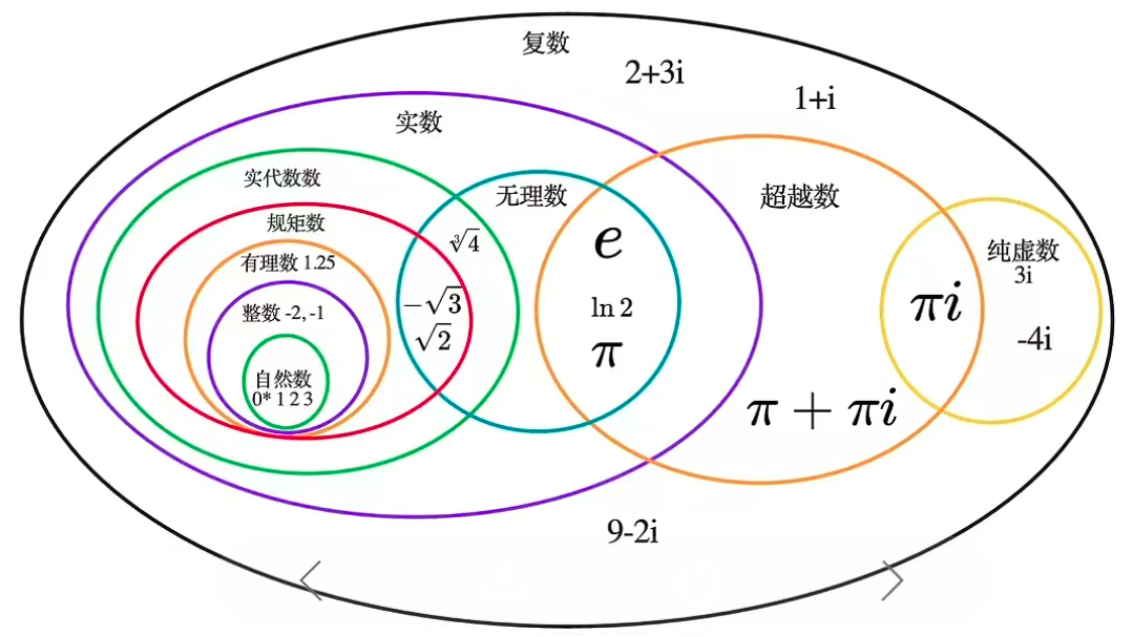
应用

尺规做图验证维维尼尔定律， 维维亚尼定理（Viviani's theorem）内容是：在等边三角形内任意一点P跟三边的垂直距离之和，等于三角形的高。

这个定理可一般化为：等角多边形内任意一点P跟各边的垂直距离之和，是不变的，跟该点的位置无关。

定理的证明很简单，用面积法即可:

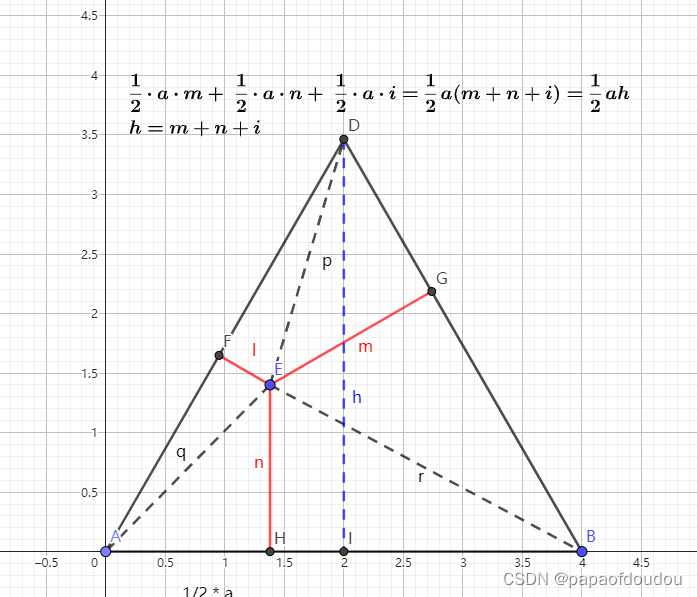
这里对证明不细说，下面验证结论：

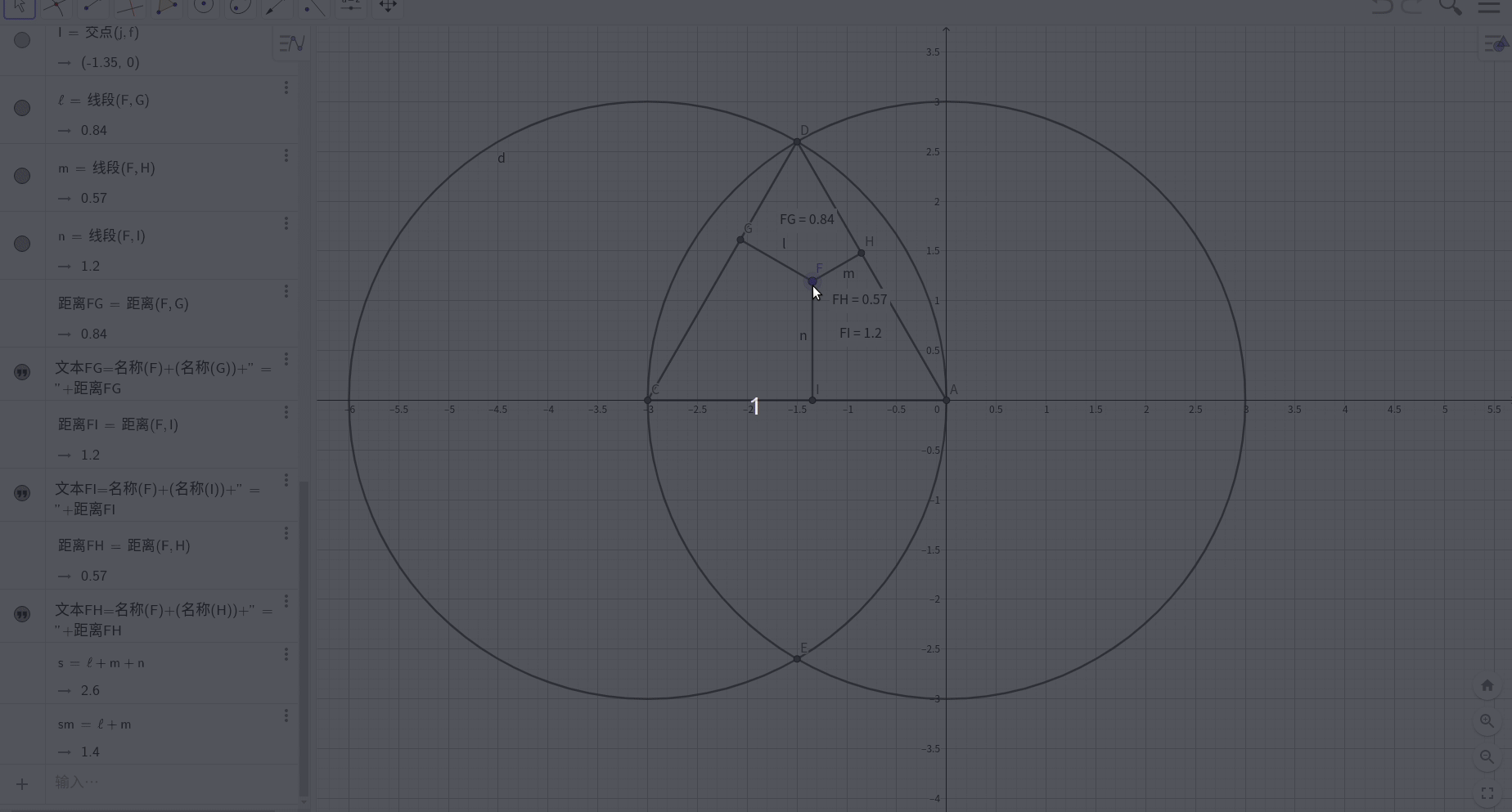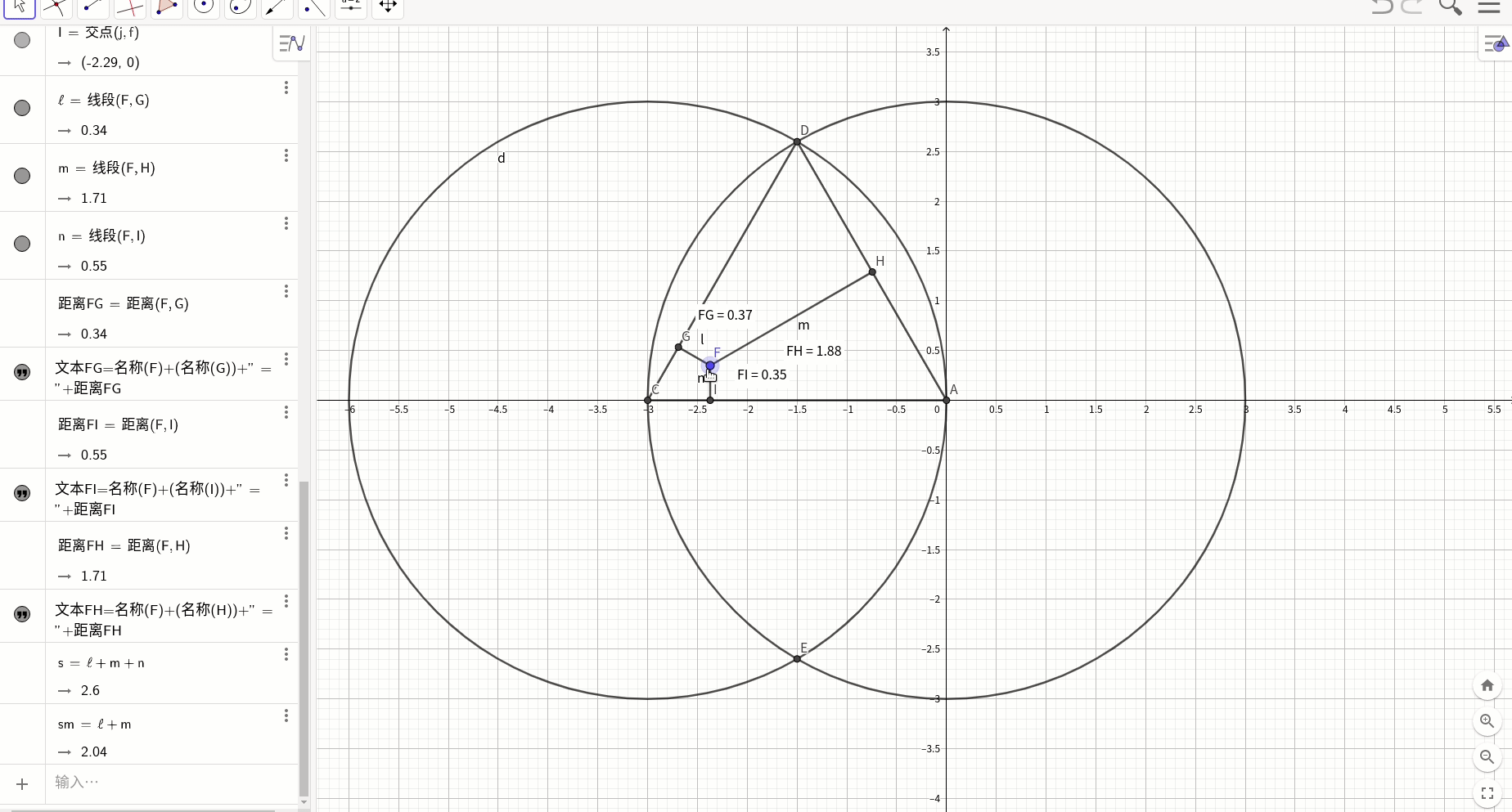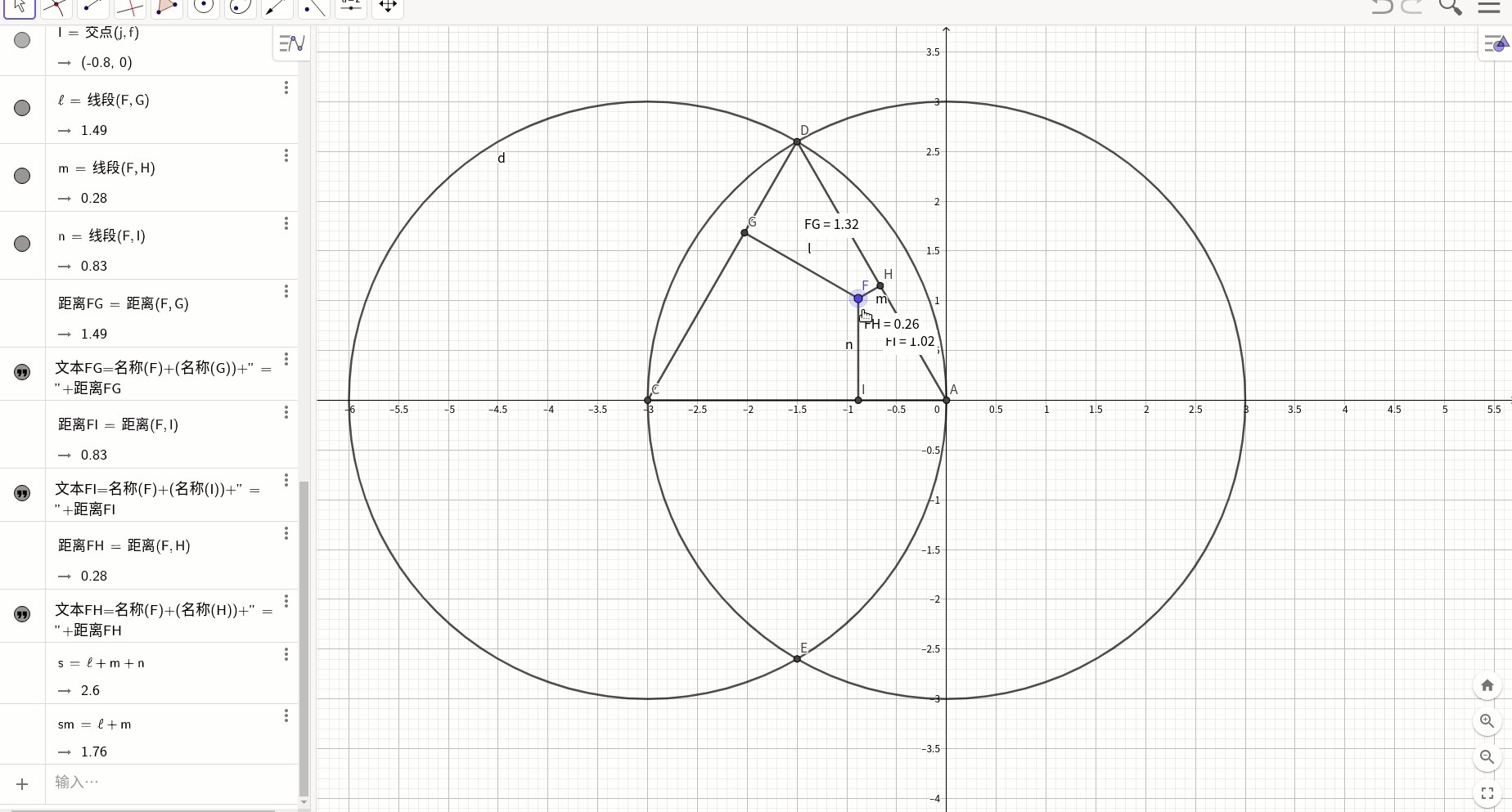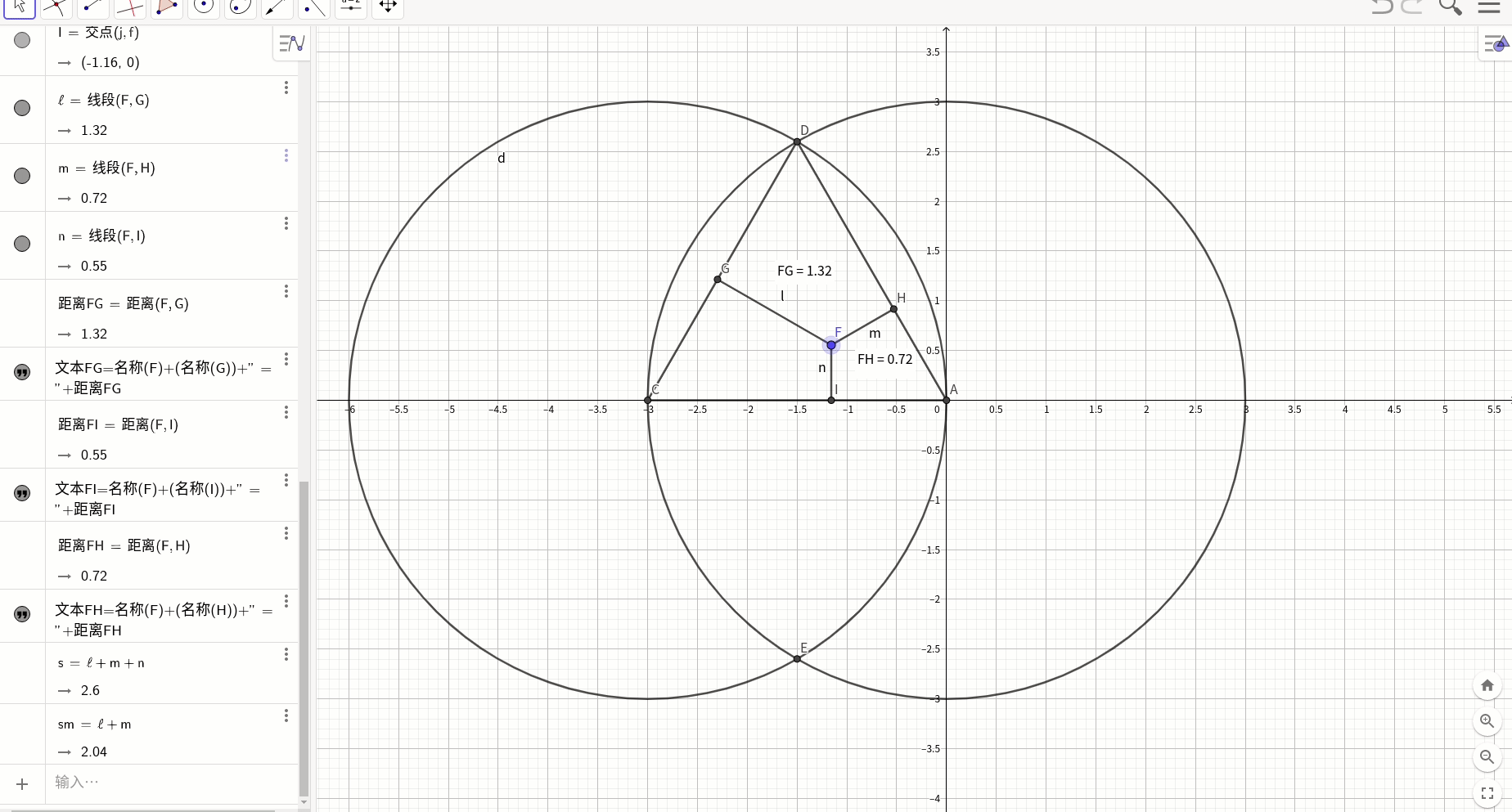
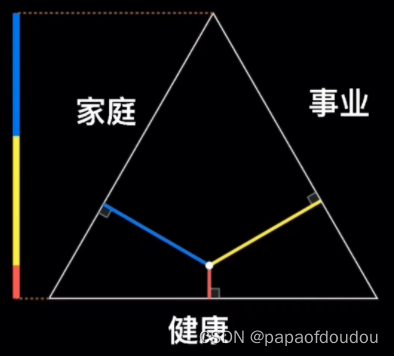
 这个定律给我们什么启示呢？人的一生的能量是有限的，要分配给家庭，健康，事业（家庭和健康这种区分是否符合MACE原则？），一方多了，必然另一方就会少。

两个有意思的作图题

1.已知三角形的三个中点位置，能否确定原三角形的三个顶点？（已知三角形三个中点位置，判断三角形是否唯一？）

如下图，三角形三个中点是A，B，C，连接AB，BC，CA， 过C作AB平行线，过A作BC平行线，过B作AC平行线，三条平行线交于D，F，E三点，三角形DFE即为原三角形。

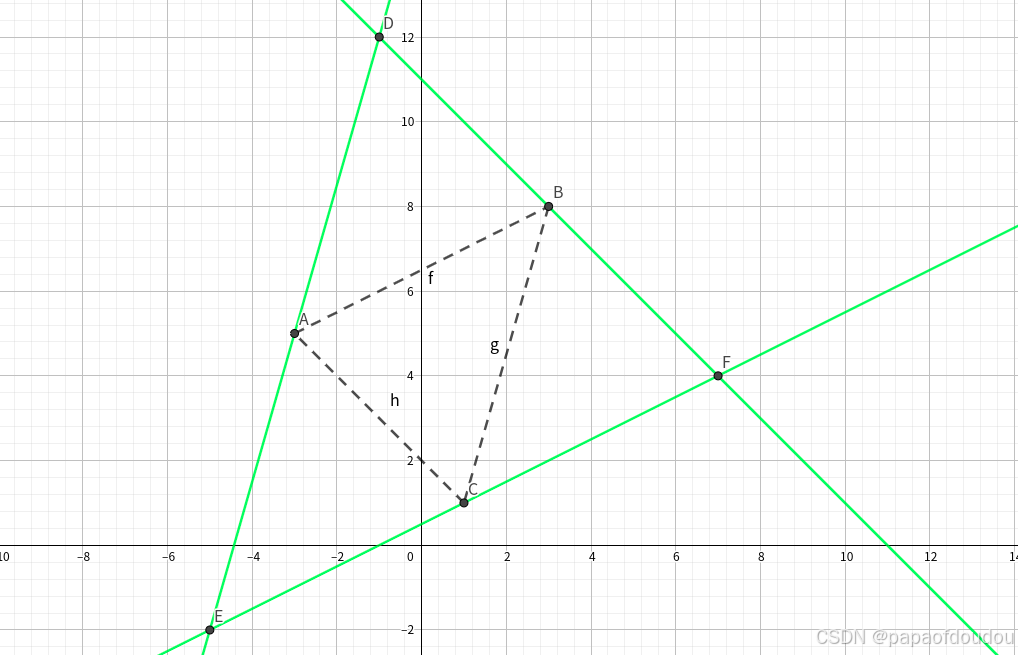
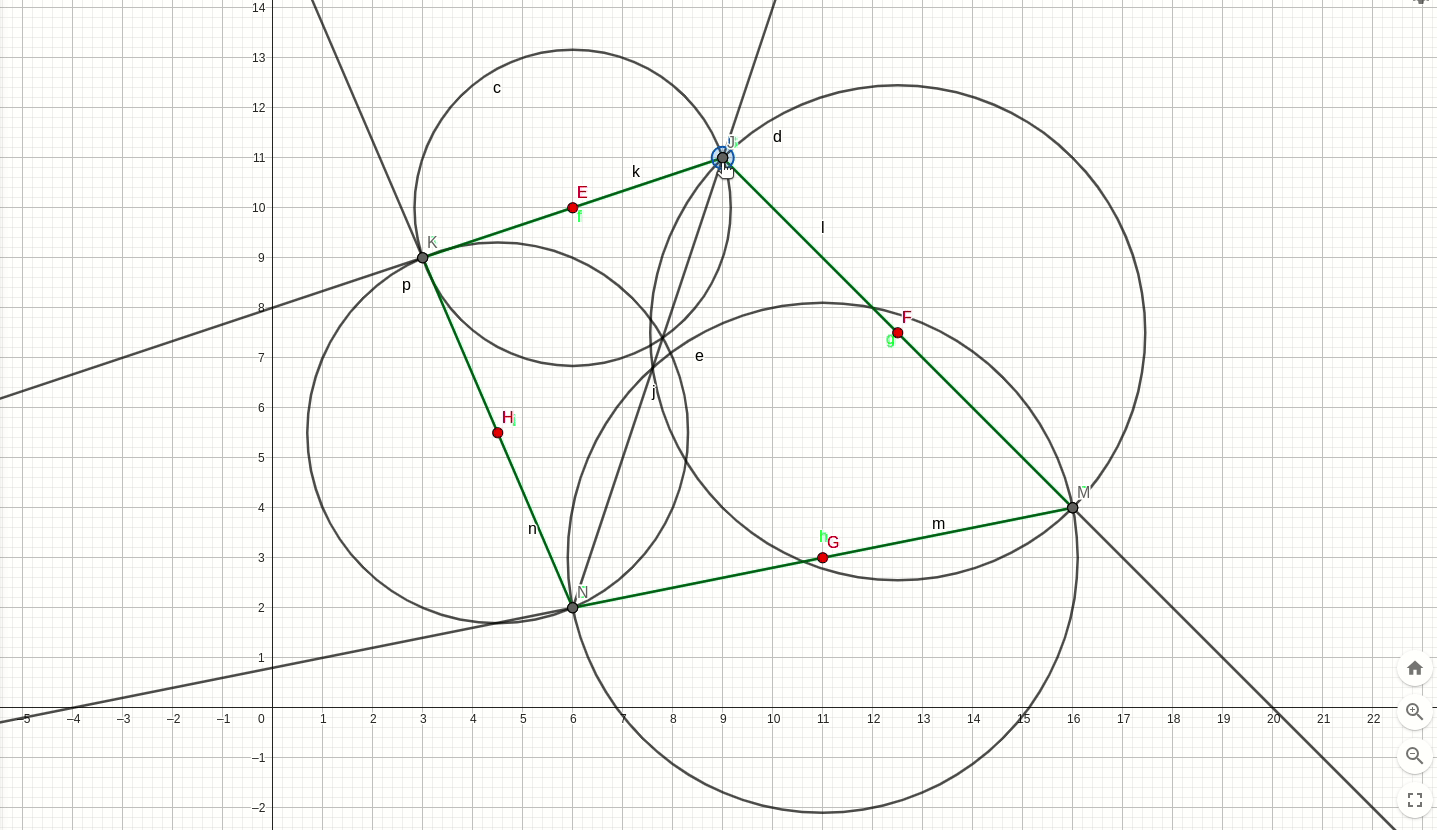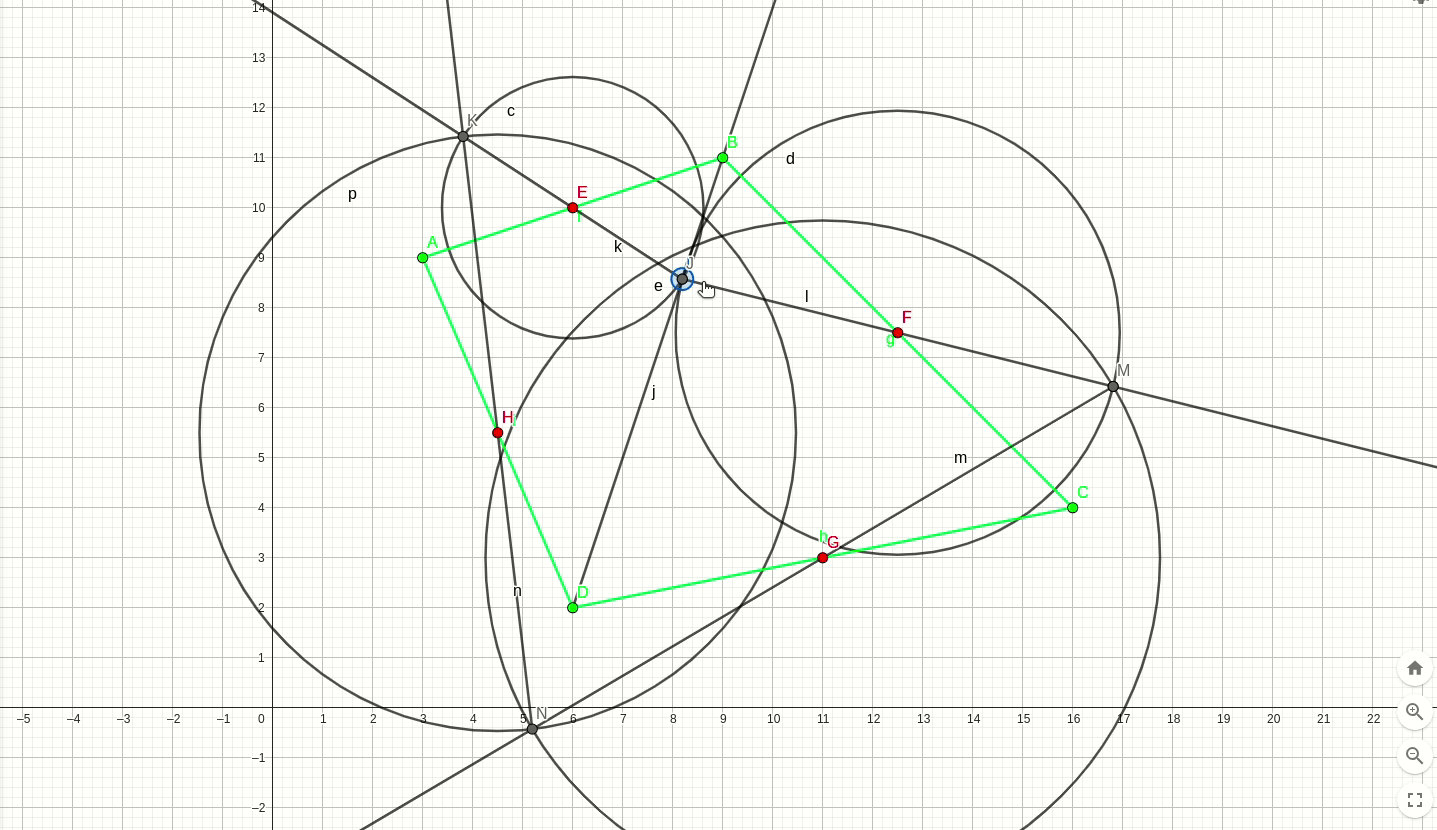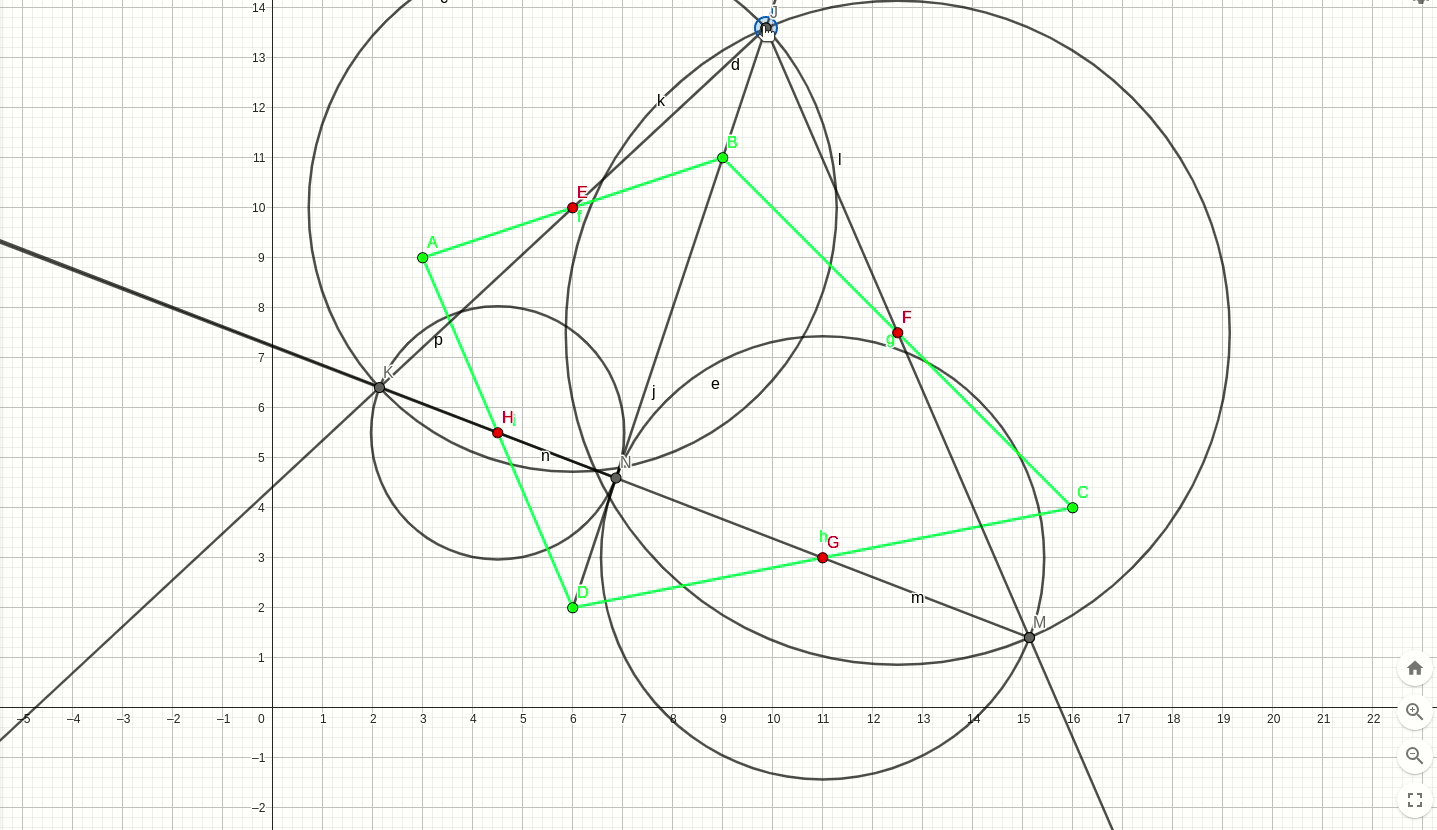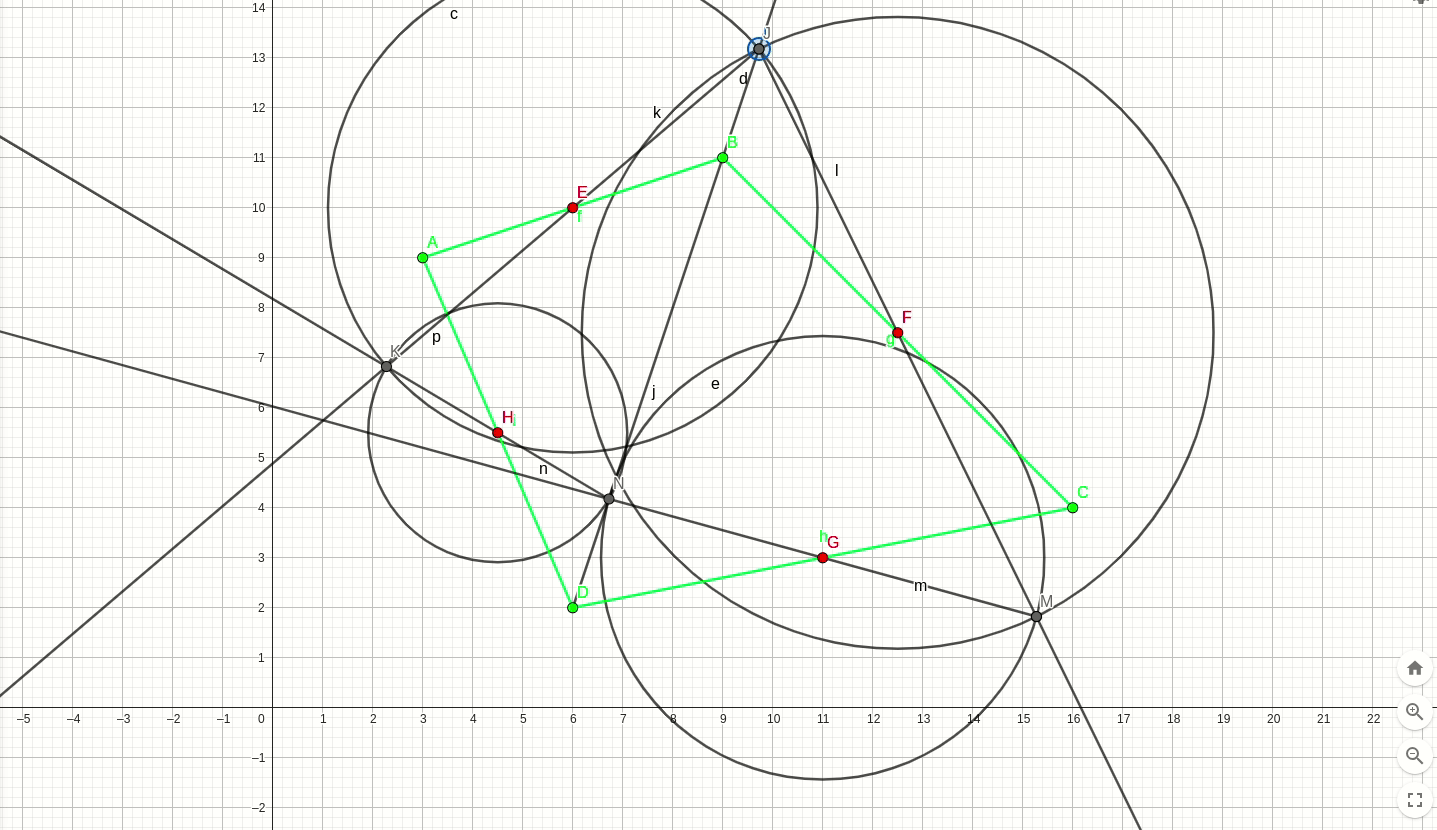
2.已知四边形四个中点，能否确定原四边形？（已知四边形的四个中点，请问原四边形是否唯一？）

答案是否定的，如下图动画，橙色的四边形是原四边形，绿色的四个点是原四边形的四个中点，在原四边形的对角线上人以取一动点M，根据条件画出一个新的四边形（红色四边形），运动过程中发现其恰好满足中点条件，如下动图。

这并不是一个巧合，我们可以选一组不同的坐标再次绘制，同样可以画出来：

尺规作图和群论

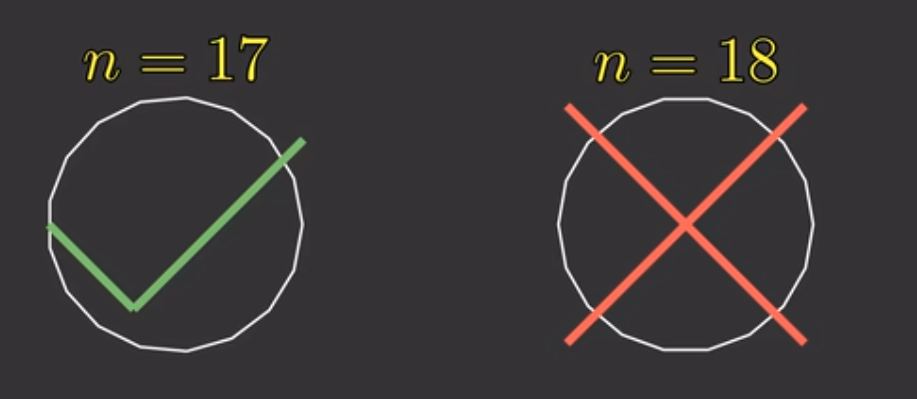
利用伽罗瓦理论，可以证明，人们可以利用尺规作图画出正17边形，但是却无法利用同样的方法画出正18边形，尽管后者看上去更“正”。

倍立方

我们知道尺规作图是不能倍立方的，但是如果允许使用绘制圆锥曲线的工具，倍立方是可以完成的。它的证明如下：

假设一个底面为axa，高为b的长方体，其体积为a^2b.我们需要作出一条线段x，满足

对式子进行代数变形：

如果能够找到a,b的两个比例中项，也就是存在：

则就能找到x,满足

然后，另b=2a，得到

就是倍立方问题。

也就是:

绘图得：

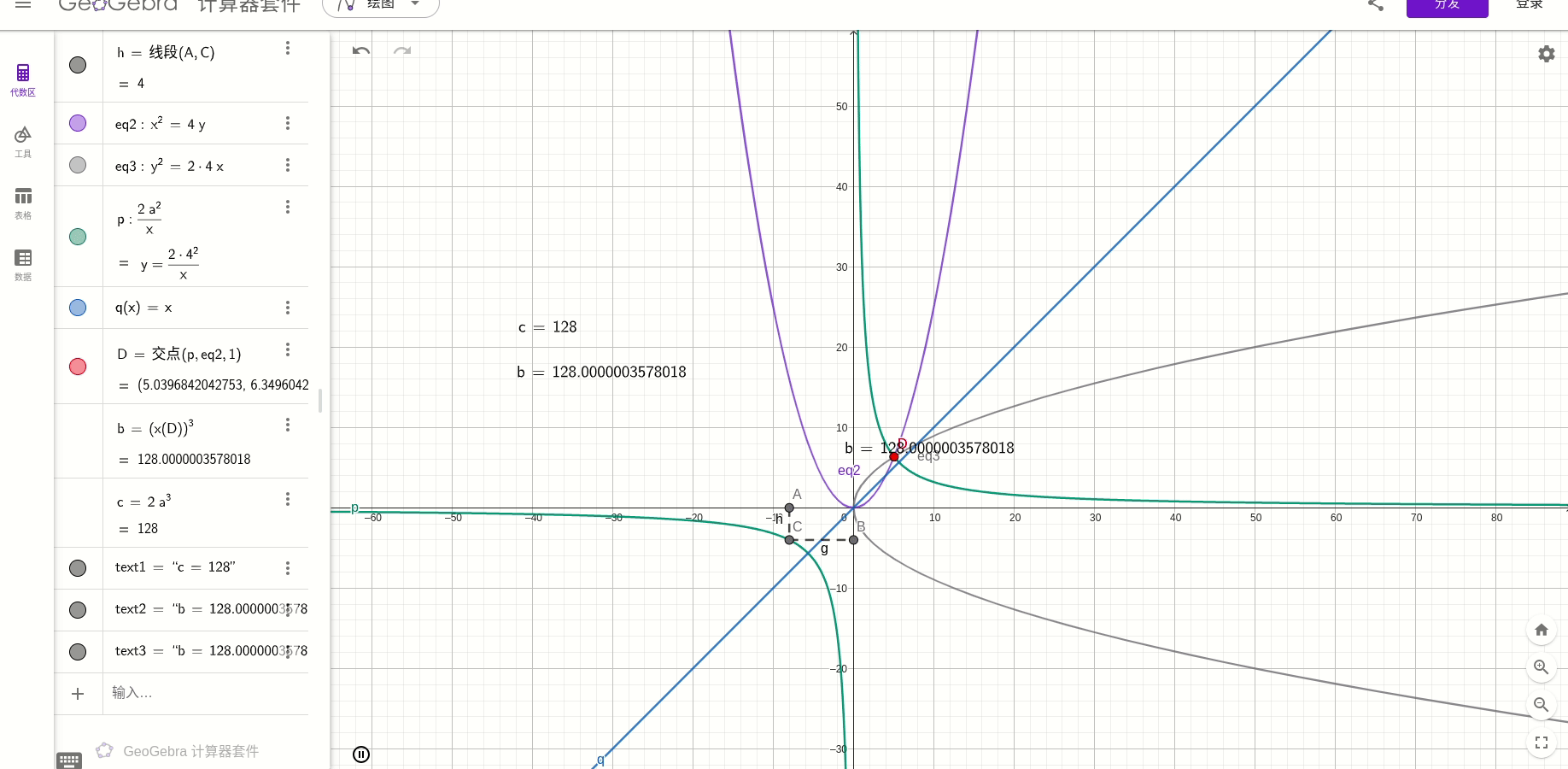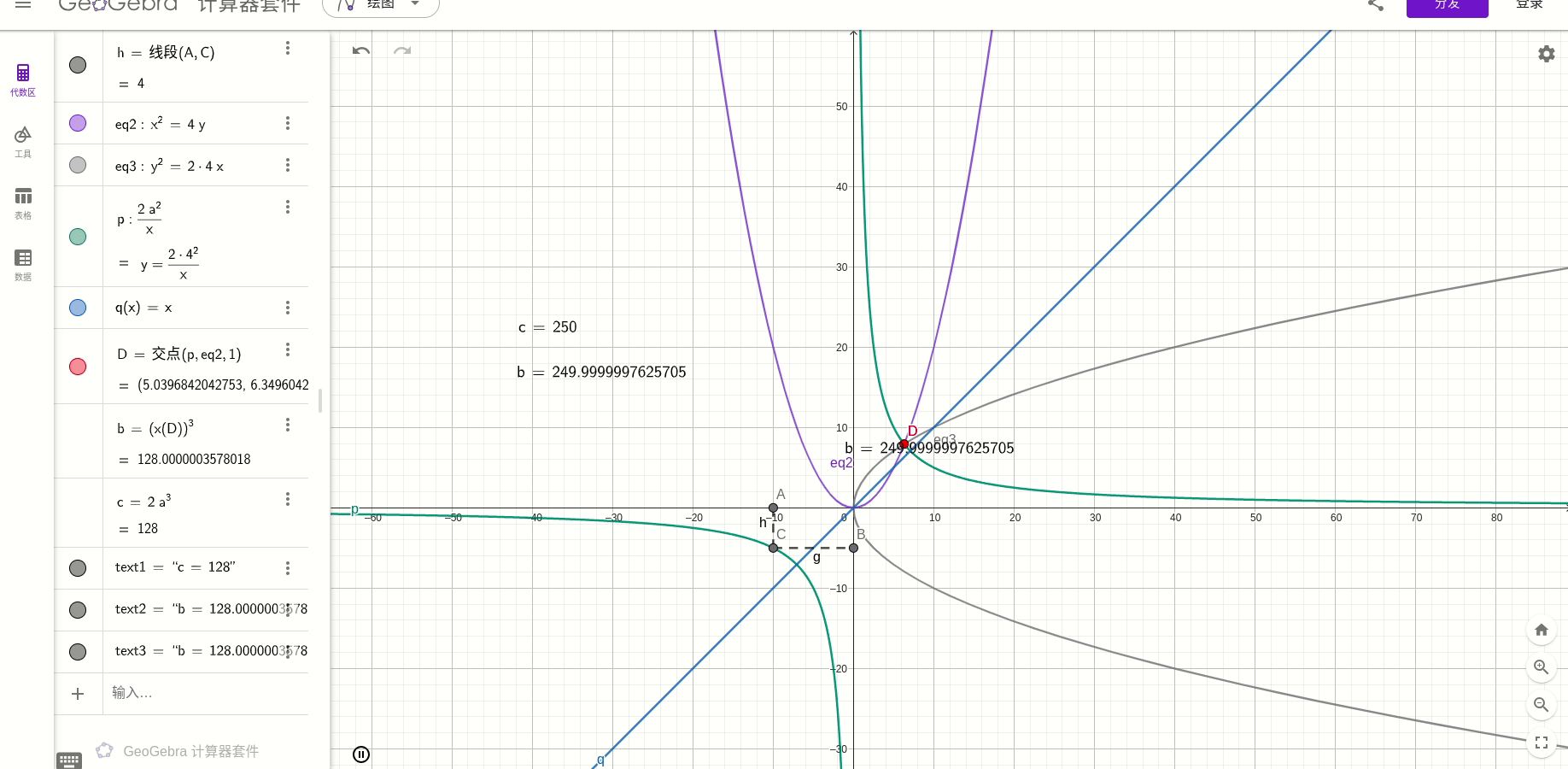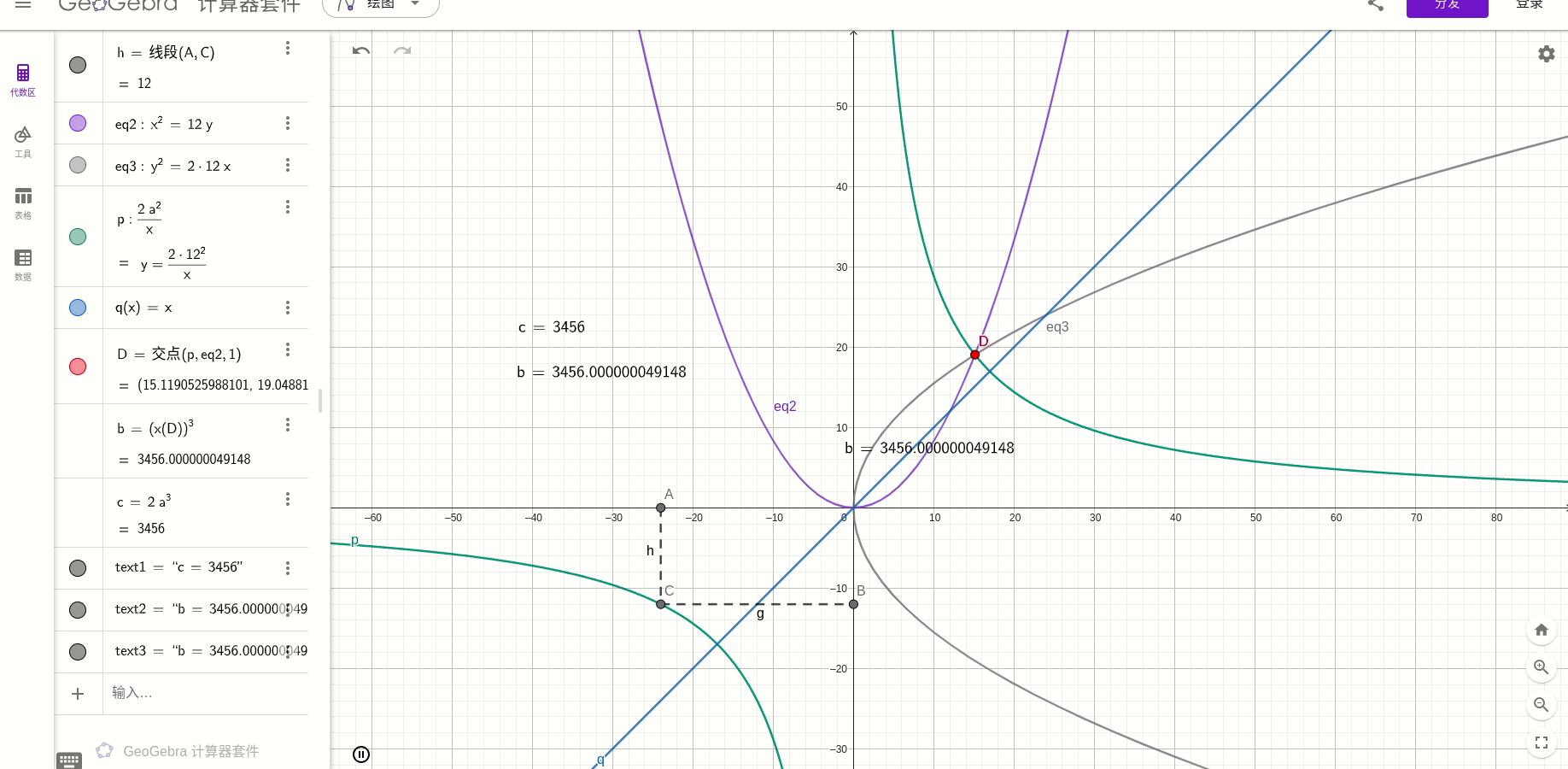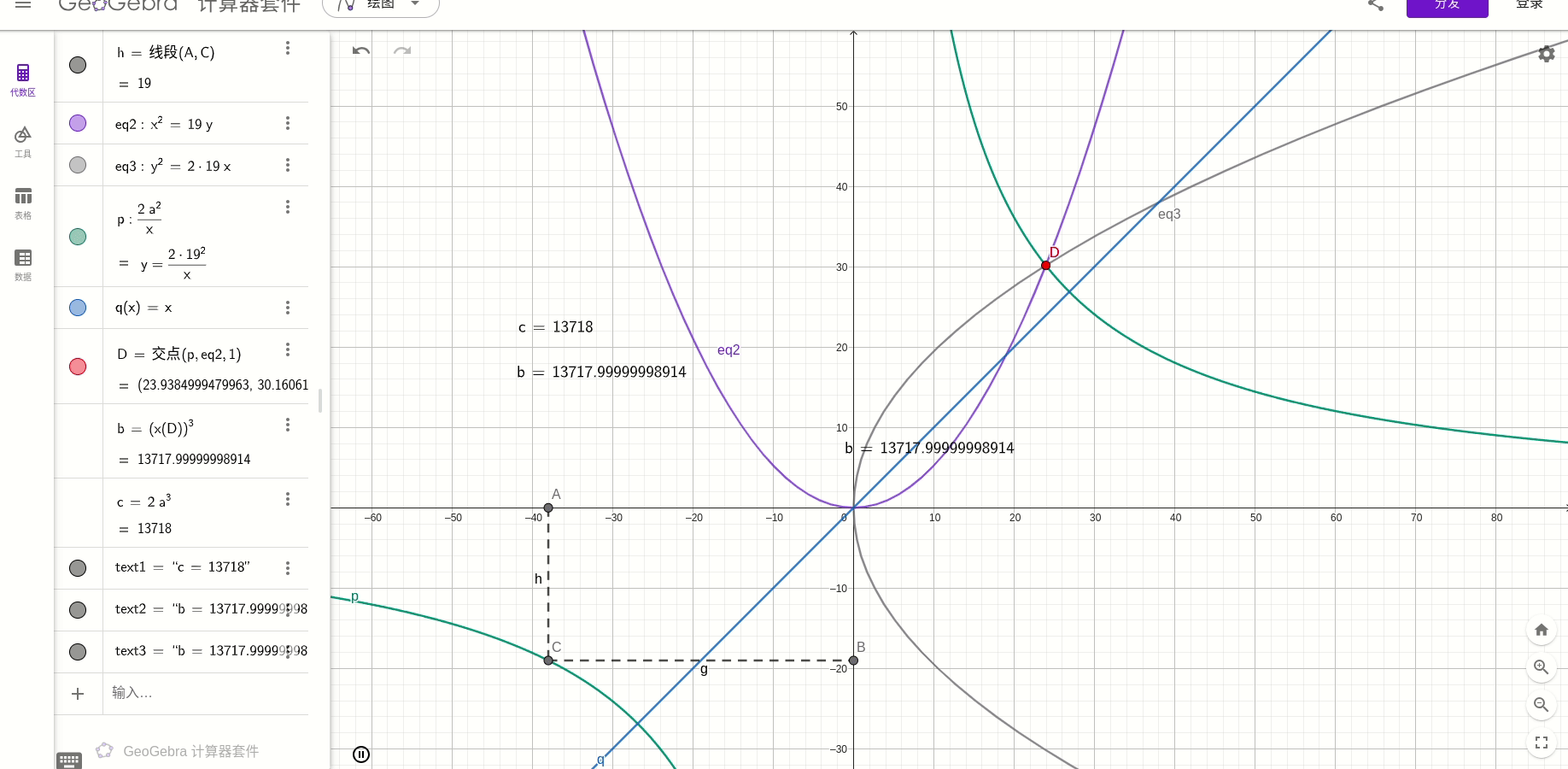
总结：

关于尺规作图的概念在某种意义下似乎是人为的，圆规和直尺肯定是作图的最简单工具，但是在几何中从来就没有只限于这些仪器，希腊数学家很早以前就意识到，如果，比如允许用直角三角板的话，某些问题，例如倍立方体问题，是能够解决的，同样也容易造出圆规以外的仪器，用以画椭圆，双曲线和更复杂的曲线，从而大大扩充了可作图的图形的范围。

---

结束