神经网络入门之感知机

感知机是神经网络（深度学习）的起源算法，因此，学习感知机的构造也就是学习通向神经网络和深度学习的一种重要思想。

这里介绍一下学习感知机的心得，并用感知机解决一些简单问题，感知机接收多个多个输入信号，输出一个信号。这里所说的信号可以想象成电流或者河流那样具备流动性的东西，像电流流过导线，向前方输送电子一样，感知机的信号也会形成流，向前方输送信息。但是，和实际的电流不同的是，感知机的信号只有流和不流两种取值，可以分别用0,1表示。

下图是一个接收两个输入信号的感知机的例子,x1,x2是输入信号，y是输出信号，w1,w2是权重，图中的圆圈称为神经元或者节点，输入信号被送往神经元时，会被分别乘以固定的权重(w1x1,w2x2),神经元会计算传送过来的信号的总和，只有当这个总和超过某个界限值时，才会输出1,也就是神经元被激活，这个界限值称为阈值。

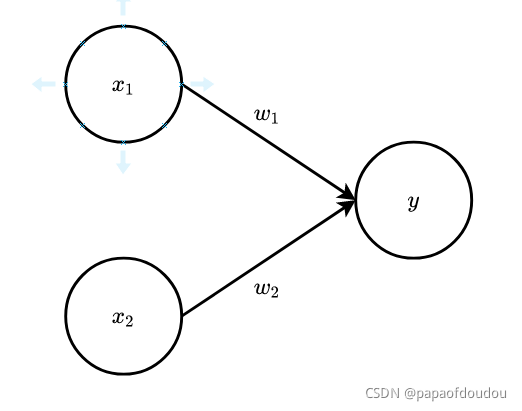
流动

感知机的多个输入信号都有各自固定的权重，这些权重发挥着控制各个信号的重要作用。也就是说，权重越大，对应该权重的信号的重要性就越高。

如果用电路做类比，权重相当于电流里所说的电阻，电阻是决定电流流动难度的参数，电阻越低，通过的电流就越大。而感知机的权重则是值越大，通过的信号就越大。不管是电阻还是权重，在控制信号流动难度这一点上的作用现在都是一样的。

用感知机来描述逻辑电路

现在考虑用感知机来解决简单问题，以与门为例，与门大家都很熟悉，其真值表如下：

0                                                        0	0
0                                                        1	0
1                                                        0	0
1                                                        1	1

如何用感知机来表示这个门呢？需要做的就是确定能满足上面真值表的的值。那么，设定什么样的值才能制作出满足上表的感知机呢？

我们可以将上面问题转换为几何问题，将真值表表示为平面笛卡尔坐标系的坐标，将求解过程转换为寻找平面上划分方式，使在这种划分方式下，真值表表达的坐标和值都落在正确的划分里面。

这是一个线性规划问题，如下图：

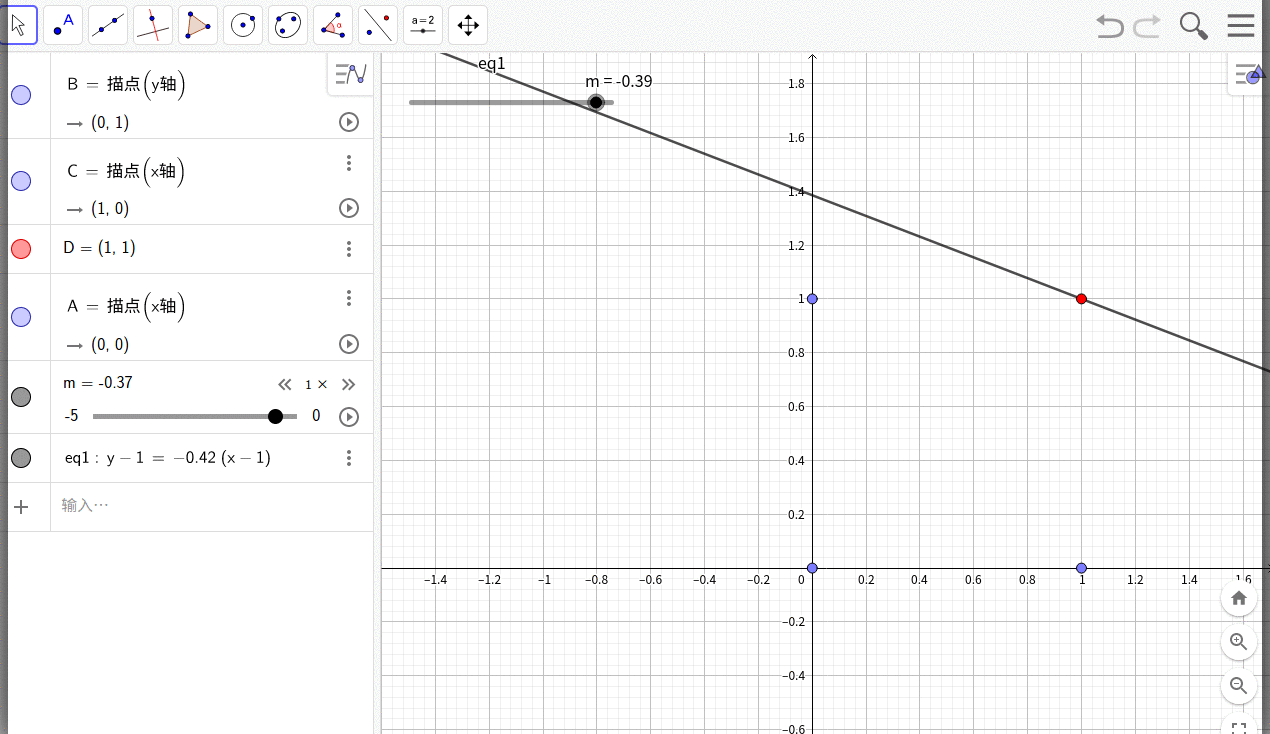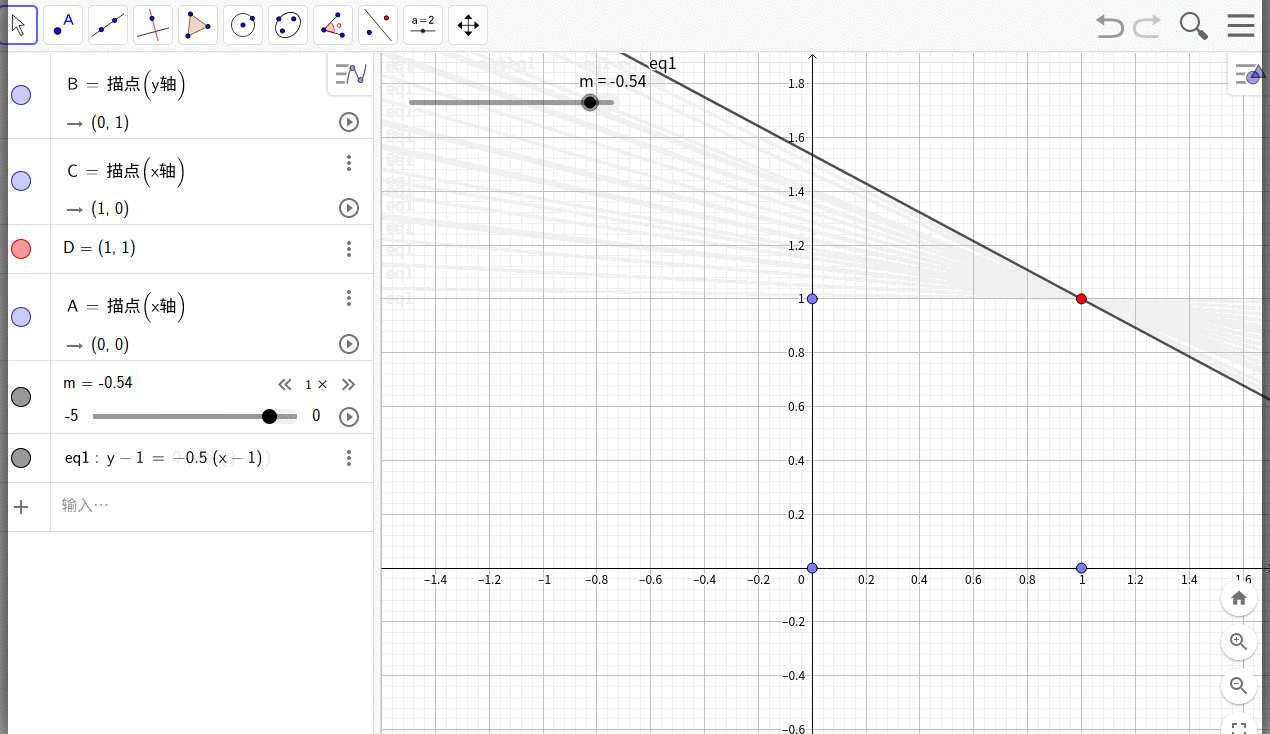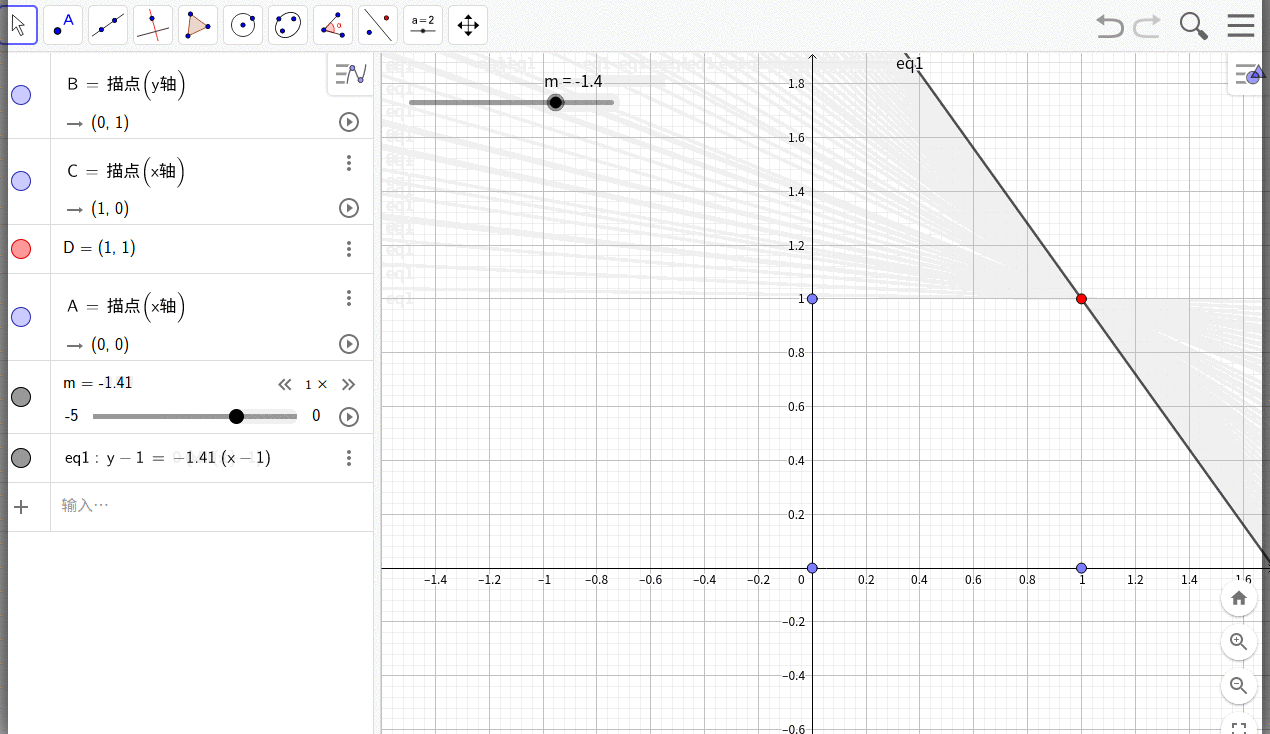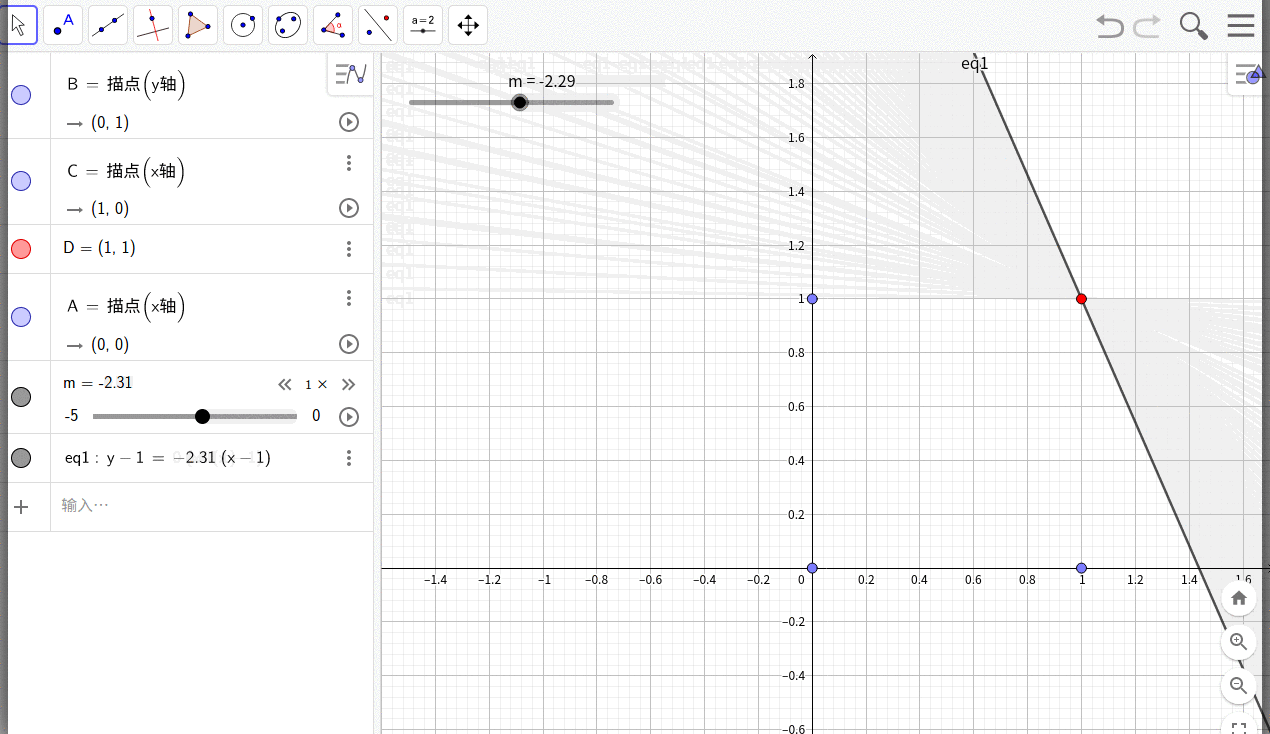
假设任何一个可行的边界线的方程为：

则：

联立：

即可得到一组可用的

同理，非门，或门以及与非门（颠倒了与门的输出）都可以通过这种方式求得无穷多组解。也就是说，这几中门都可以表达成如下的形式，区别仅仅在于 的不同。

 根据以上，我们总结出，与门，与非门，或门的感知机构造是一样的，实际上，这三种门电路只有承诺书的值不同，也就是说，相同构造的感知机，只需要通过适当地调整参数的值，就可以像变色龙演员表演不同的角色一样，变身为与门，与非门，或门。

是不是所有的逻辑电路都可以这样做呢？答案是否定的。

感知机的局限性：

考虑一下异或门，它的真值表如下：

0                                                        0	0
0                                                        1	1
1                                                        0	1
1                                                        1	0

在坐标系中表示为：

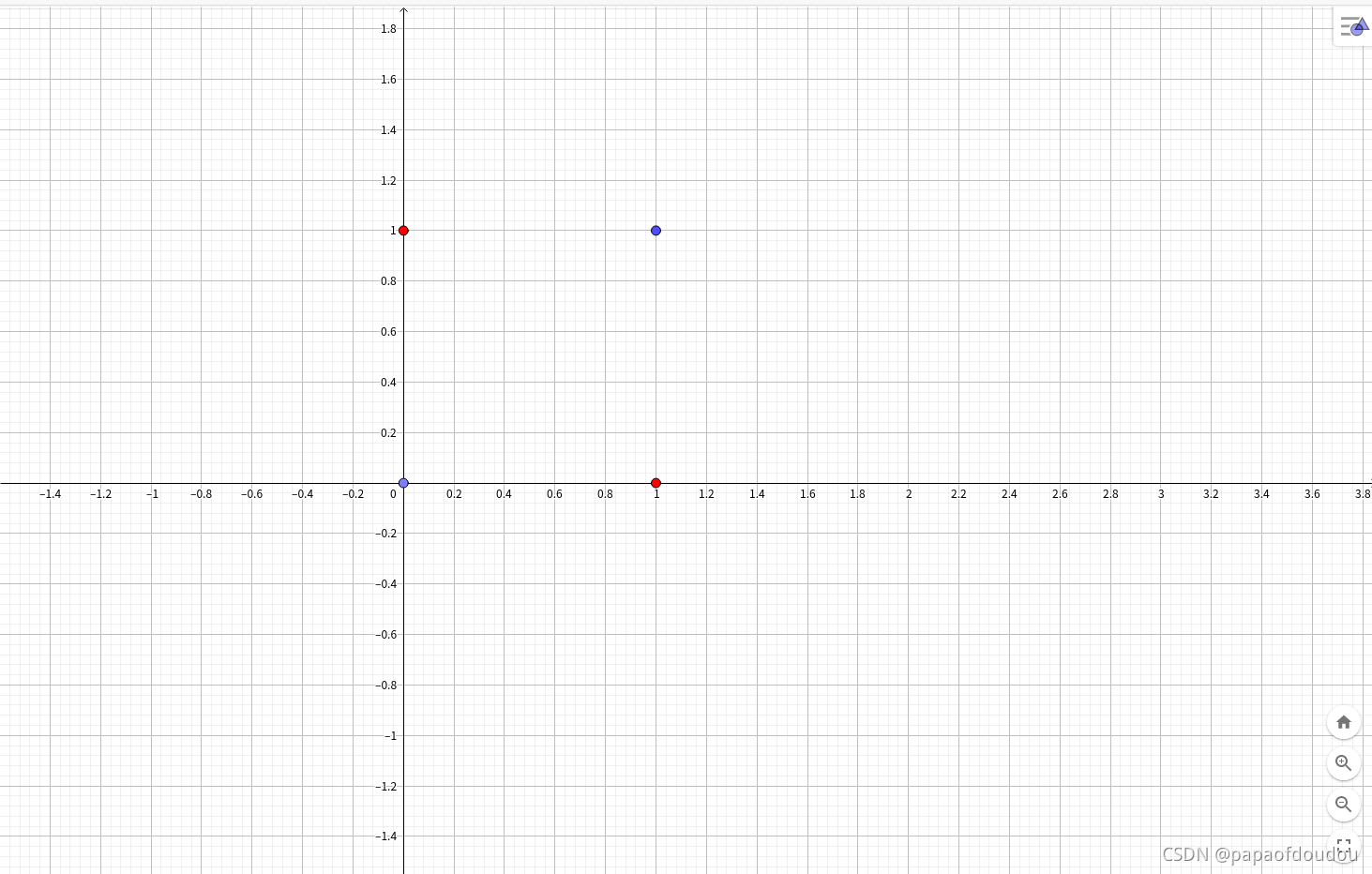
 很明显，异或门的整体分布，使得我们根本无法找到一条直线，可以将红色和蓝色的点分开。

线性和非线性

前面讲的感知机的局限性就在于它只能表示由一条直线分割的区间，这种叫做线性区间，无法表示曲线区间，也就是非线性区间。

感知机不能表示异或门让人深感遗憾，但也无需悲观，实际上，感知机的绝妙之处在于，它可以叠加层。通过已有的各种门组合来表达。

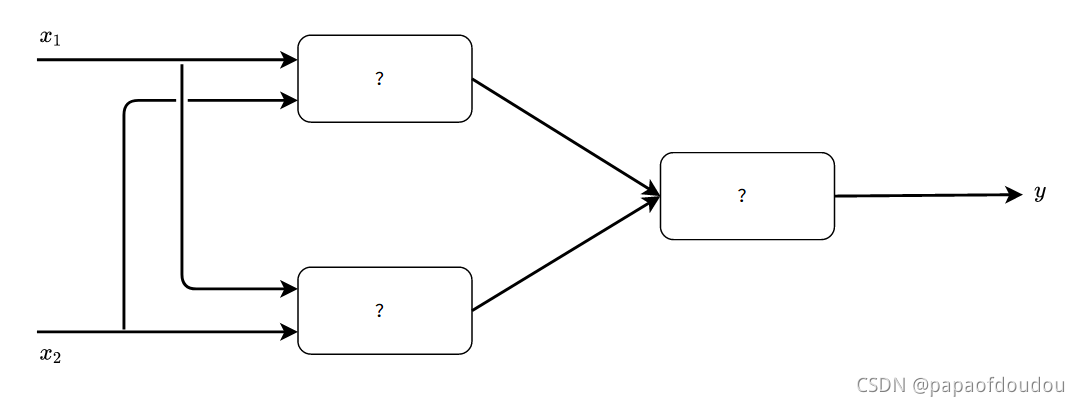
 将与门，与非门，或门带入到？中，就可以实现异或门。

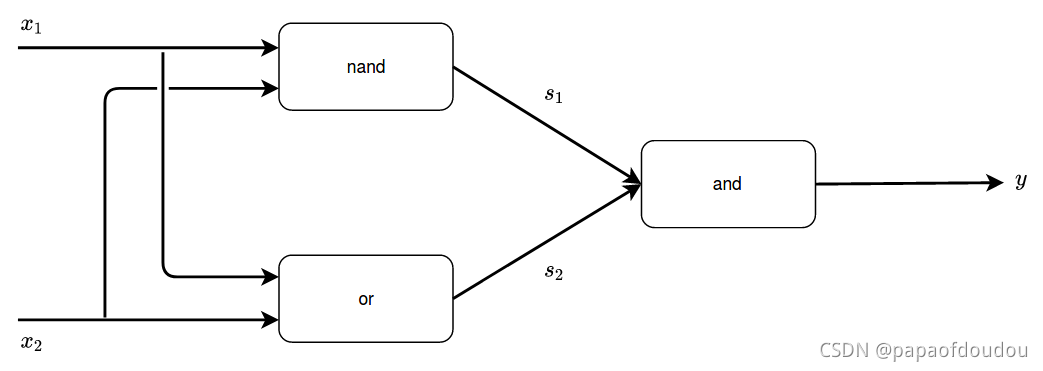
 它的真值表如下：

0                   0	1                   0	0
1                   0	1                   1	1
0                   1	1                   1	1
1                   1	0                   1	0

多层感知机可以实现比之前见到的电路更加复杂的电路，比如，进行加法运算的加法器也可以用感知机实现，此外，将二进制转换为十进制的编码器，满足某些条件就输出为1的电路，等等都可以通过感知机来实现。

计算机是处理信息的机器，向计算机中输入一些信息后，它会按照某种既定的方法进行处理，然后输出结果，所谓的”按照某种特定的方法进行处理“是指，计算机和感知机一样，也有输入和输出，会按照某个既定的规则进行计算。

人们一般会认为计算机内部的处理非常复杂，而令人惊异的是，实际上只需要通过与非门的组合，就能再计算机进行的处理。这一令人吃惊的事实说明了什么呢？说明使用感知机也可以表示计算机，前面说的，与非门可以通过感知机来实现，也就是说，如果通过组合门电路可以实现计算机的话，那么通过组合感知机也可以表示计算机。

理论上证明，只需要2层感知机就能改构造计算机，研究证明，2层感知机可以表示任意函数。

前面介绍感知机的原理使用了线性分类的思想，可是我们知道，对于一个神经网络来说，不管它有多少层，最终叠加后仍然是线性的，具体证明可参考这篇文章

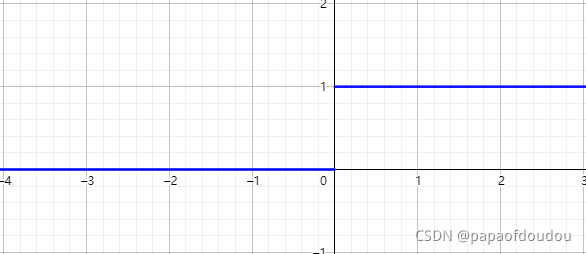
为什么神经网络需要激活函数层？_tugouxp的专栏-优快云博客这个问题的原因，很多书上讲，是为了引入非线性，也就是说，只有引入激活函数，网络才能具有非线性特征，那疑问就来了，没有激活函数层，就没有非线性了吗？是否有方式证明？以为下面的网络为例，它的每一层都是全连接层，并且没有激活函数层，我们列出各层之间的数据关系公式：第一层输出：第二层输出：...最后一层：逐层代入得到：由于Wn,Bn都为常阐述，所以，根据上式可以看出，输出是输入的线性函数，所以网络一定是线性的，不具备非线性特征。从而我们证明了，为什么一定要引入激活https://blog.youkuaiyun.com/tugouxp/article/details/120777214那么，为什么两层的感知机可以实现非线性的结果呢?原因是感知机中隐含使用了阶跃函数作为激活函数，如果将接跃函数换成sigmoid函数的话，那么感知机就立刻变成了神经网路了，可以说激活函数是否使用的是阶跃函数是区分网络是否属于感知机的依据，这是因为，阶跃函数并非像sigmoid函数那样处处可导，即便是在可导的区域，它的导数也是恒值，这样会导致损失函数（识别精度）的变化，无法反向传播出去，如果使用阶跃函数作为激活函数，神经网络的学习将无法进行。

而sigmoid函数则不同，它的导数处处存在且不为0，不仅输出值是连续变化的，而且曲线的斜率也是连续变化的，这对于神经网络的学习是非常重要的。

结束！