为什么神经网络需要激活函数层？

原创已于 2022-08-06 09:52:56 修改 · 置顶 · 1.5k 阅读

1 ·

CC 4.0 BY-SA版权

文章标签：

#神经网络 #深度学习

于 2021-10-15 09:47:49 首次发布

嵌入式系统同时被 2 个专栏收录

354 篇文章

订阅专栏

人工智能

155 篇文章

订阅专栏

本文探讨了神经网络为何需要激活函数，指出没有激活函数的网络仅能实现线性变换，等价于单层网络。通过数学证明，阐述了激活函数引入的非线性特性对提升网络能力的重要性。

这个问题的原因，很多教材上讲是为了引入非线性，也就是说只有引入激活函数层建立的网络才具有非线性特征，那疑问就来了，没有激活函数层就没有非线性了吗？如果答案是肯定的话，是否存在严谨的理论证明？

以为下面的网络为例，它的每一层都是全连接层，并且没有激活函数层，我们列出各层之间的数据关系公式：

第一层输出：

$\vec{y}=W_1\vec{x}+\vec{b_1}$

第二层输出：

$\vec{mid}=W_2\vec{y}+\vec{b_2}$

...

最后一层：

$\vec{o}=W_n\vec{z_n}+\vec{b_n}$

逐层代入得到：

$\boldsymbol{\\ \vec{o}=W_n\vec{z_n}+\vec{b_n}=Wn(W_{n-1}\vec{z_{n-1}} + \vec{b_{n-1}})+\vec{b_n} = \cdots = W_nW_{n-1}W_{n-2}\cdots W_1\vec{z_1} +W_n\vec{b_{n-1}}+W_nW_{n-1}\vec{b_{n-2}}+\cdots + W_nW_{n-1}\cdots W_{2}\vec{b_1} +\vec{b_n}}$

由于Wn,Bn都为常函数，所以，根据上式可以看出，输出是输入的线性函数，所以网络一定是线性的，不具备非线性特征。

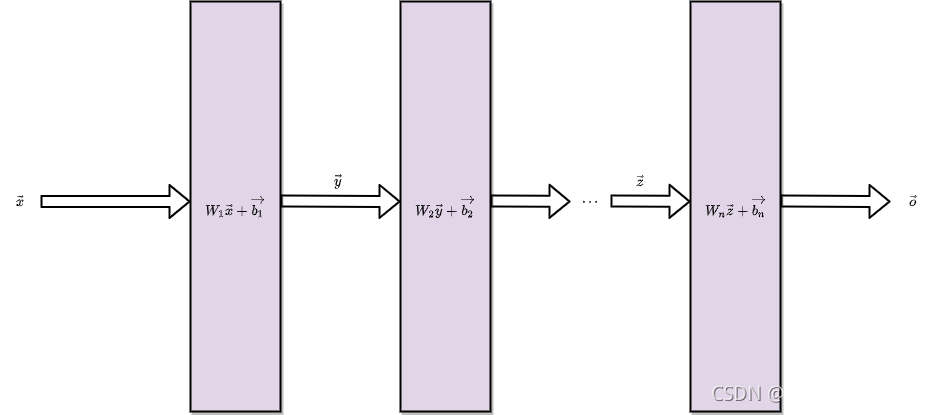
从联立后的式子可以看出，虽然神经网络引入了隐藏层，却依然等价于一个单层神经网络,输入和输出依然是线性关系。

上述问题的根源在于全连接层只是对数据做仿射变换（affine transformation)，而多个仿射变换的叠加仍然是一个仿射变换。解决问题的一个方法是引入非线性变换，例如对隐藏变量使用按元素运算的非线性函数进行变换，然后再作为下一个全连接层的输入。这个非线性函数被称为激活函数，在代码中，全连接层经常被叫做affine layer（仿射层），也是这个意思。

上面的证明过程依赖于数形结合，下面用解析的方式，用更加数学的语言来证明这个结论:

对于一个没有激活函数的网络，假设

$y^k_j$

是第k层网络的第j个神经元输出， $x_1,x_2,\cdots,x_n$ 是这层网络的输入，所以， $y^k_j$ 可以表示为输入的线性函数：

$y^k_j(x_1,x_2,\cdots,x_n)=b^k_j+\sum_{i=1}^{n}w^k_{ji}x_i$

然后，另g为下一层的网络输出，则针对下一层来说， $y^k_1\ \ \ y^k_2 \ \ \ \cdots \ \ y^k_m$ 为这一层的输入，所以：

$\\ g^{k+1}_s(y^k_1\ \ \ y^k_2 \ \ \ \cdots \ \ y^k_m)=b^{k+1}_s+\sum_{i=1}^{m}w^{k+1}_{si}y^k_i=b^{k+1}_s+\sum_{i=1}^{m}w^{k+1}_{si}\bigg(b^k_i+\sum_{p=1}^{n}w^k_{ip}x_p\bigg) \\ = b^{k+1}_s+\sum_{i=1}^{m}w^{k+1}_{si} b^k_i+\sum_{i=1}^{m}w^{k+1}_{si} \sum_{p=1}^{n}w^k_{ip}x_p=b^{k+1}_s+\sum_{i=1}^{m}w^{k+1}_{si} b^k_i+\sum_{p=1}^{n}x_p \sum_{i=1}^{m}w^{k+1}_{si} w^k_{ip} \\= c_0 +\sum_{i=1}^{n}c_ix_i$