有趣的复平面变换

最新推荐文章于 2024-09-26 20:41:45 发布

papaofdoudou

最新推荐文章于 2024-09-26 20:41:45 发布

阅读量3.3k

点赞数 9

CC 4.0 BY-SA版权

分类专栏：数学 AI 工程

版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。

本文链接：https://blog.youkuaiyun.com/tugouxp/article/details/110160055

数学同时被 3 个专栏收录

154 篇文章

订阅专栏

53 篇文章

订阅专栏

24 篇文章

订阅专栏

Geogebra画了几个复平面上的变换图形，感觉特别有意思，对非线性空间的变换又有了更加几何化的理解，先来看第一个:

1.

　 $f(z)=\frac{z^2}{2}$ 　在复平面的变换图形,下图展示的是一组平行于坐标轴的线段，经过f(z)变换后的图形，是不是很漂亮？

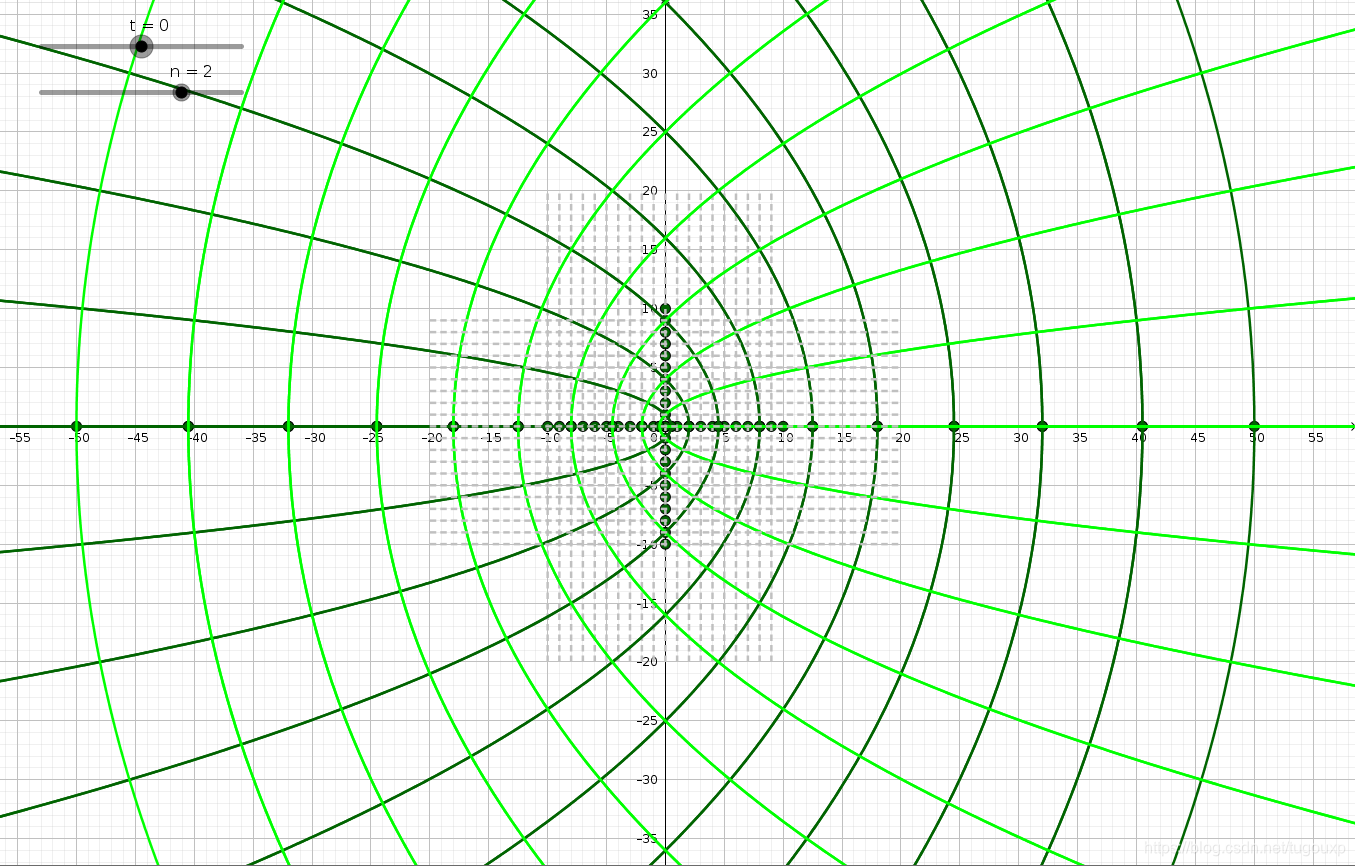
可以代数推导一下:

对于

$z=x+yi$

$f(z)=\frac{x^2-y^2}{2}+xyi$

所以，坐标轴x=0映射为负半轴，y=0映射为正半轴，原点仍在原点。

坐标网格分别映射为左右复平面上的弯曲抛物线，以x=a为例:

$z=a+mi$

则

$f(z)=\frac{a^2-m^2}{2}+ami$

点

$(\frac{a^2-m^2}{2},am)$ 在复平面上的轨迹是:

$x=\frac{a^4-y^2}{2a^2}$

确实是一条抛物线。

用极坐标的方式可能更容易理解：

设

$z=r\angle \theta$

则：

$f(z)=\frac{z^2}{2}=\frac{r^2}{2}\angle 2\theta$

可以想象一下变换模变为 $\frac{r^2}{2}$ ,幅角扩大２倍的样子．

后续会不断更新新的复平面变换图形。

２． $f(z)=e^z$

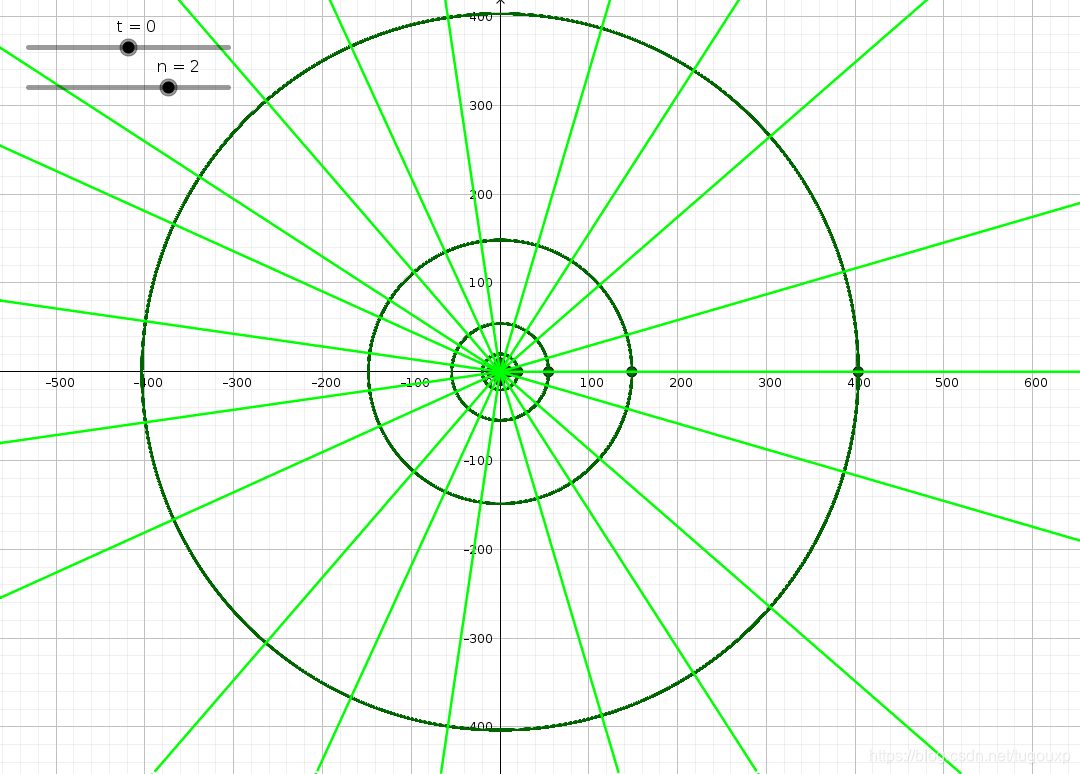
平行于x轴的直线虚部不变，也就是幅角不变，映射为原点开始，幅角一定的射线。

平行于y轴的直线实部不变，虚部可变，映射为以 $e^{real(z)}$ 为半径的圆周。

虚部只对旋转有贡献，实部在决定点距离原点的位置！

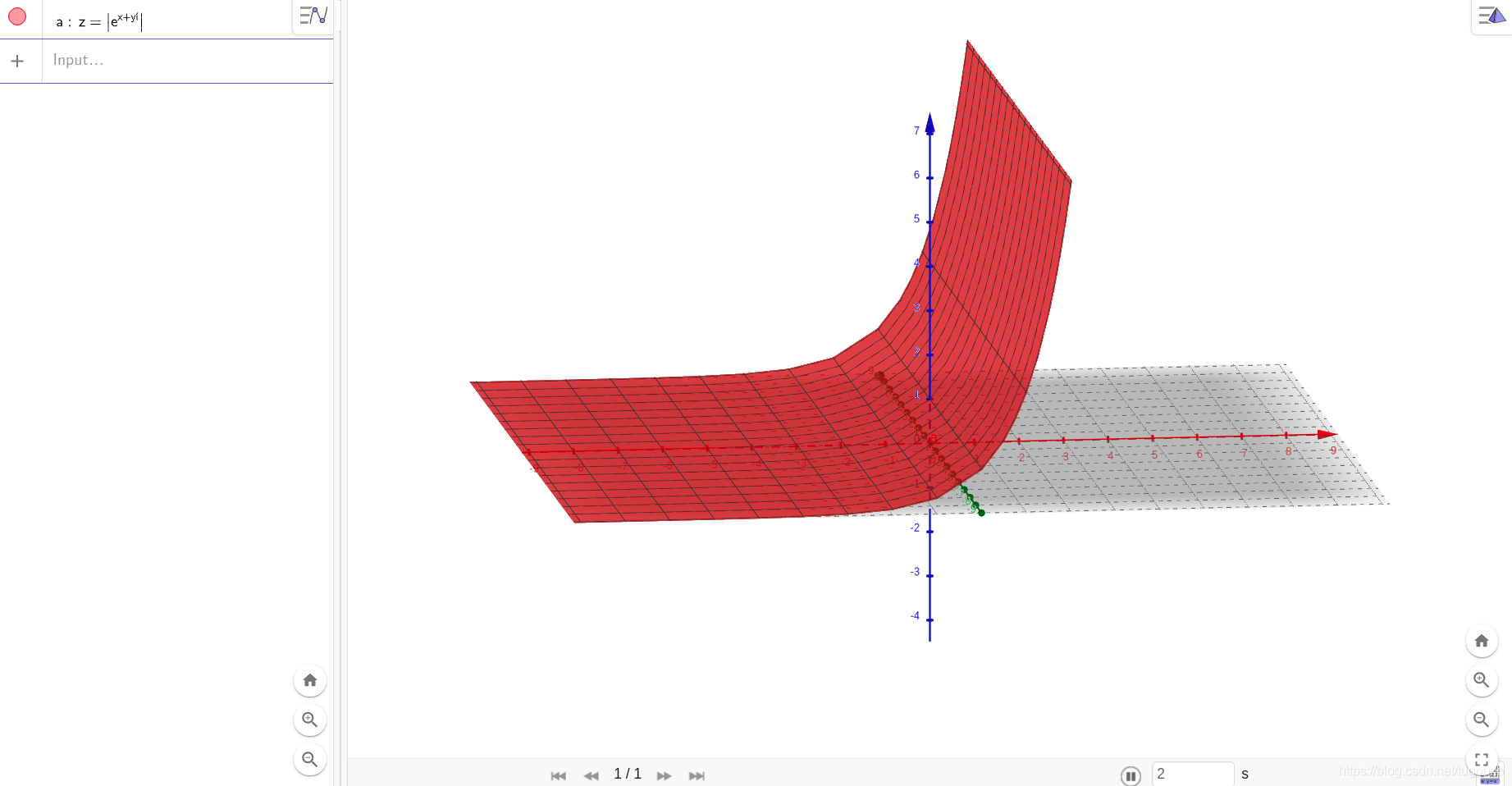
上面是复平面到复平面的变换，下面图示的是 $f(z)=e^z$ 的模曲面方程，和上图有同样的信息，你能看出来吗？

有意思的是，上面所说的两个变换前后，互相垂直的线再变换后仍然是互相垂直的，这种变换也叫＂保角变换＂，再复变函数里面，保角变换的特性是很强的特性，几乎等价于函数可微．

评论

被折叠的条评论为什么被折叠?

到【灌水乐园】发言

查看更多评论

添加红包

成就一亿技术人!

hope_wisdom

发出的红包

打赏作者

papaofdoudou 你的鼓励将是我创作的最大动力

¥1 ¥2 ¥4 ¥6 ¥10 ¥20

扫码支付：¥1

获取中

扫码支付

您的余额不足，请更换扫码支付或充值

实付元

使用余额支付

点击重新获取

扫码支付

钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。