关于集合悖论的通俗理解

集合分为两类，第一类集合的特征是:　集合本身又是集合中的元素。

属于第一类的例如:所有集合所组成的集合,应该是一个递归定义,具有自吞性：

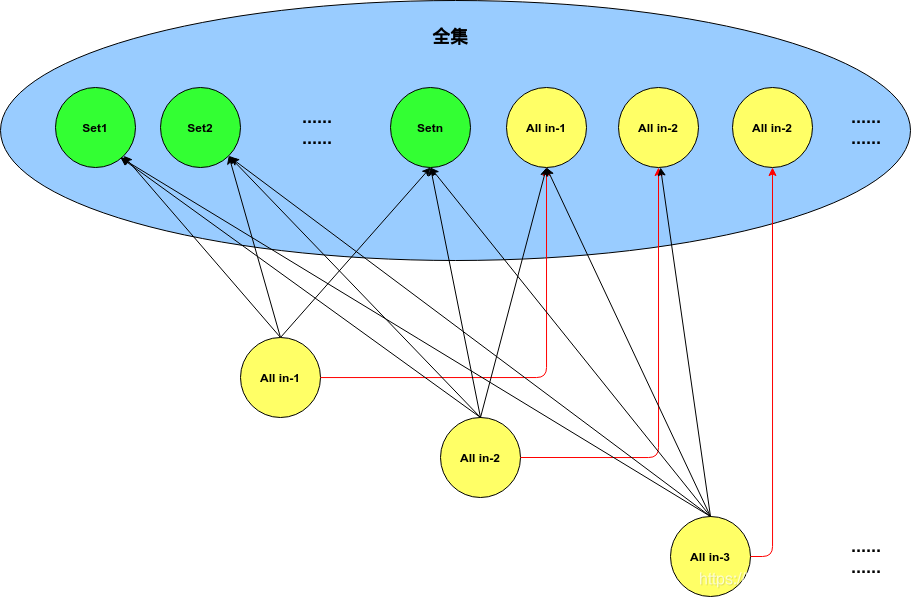
第二类集合的特征是，集合本身不是集合的元素，属于第二类的例如:直线上点的集合，所有的男人的集合等等，这种没有自吞性的形式比较普遍：

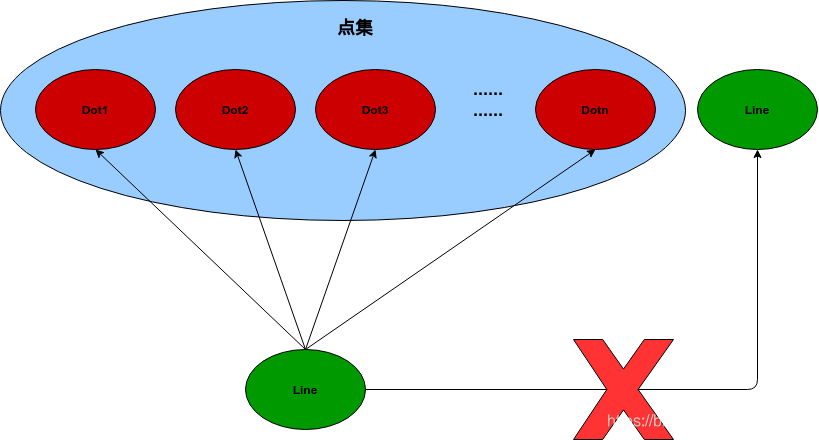
OK,问题来了，如果现在有一个集合A，是所有第二类集合构成的集合，也就是其集合中的元素本身也是集合，而且这个集合是第二类集合，那么它属于哪一类呢？

首先，我们假设它属于第二类，既然它属于第二类，所以它一定满足第二类的
特征，就是它本身不存在于它的子集中（不是它的任何一个元素）,也就是说它不是第二类集合，但这显然和前提，也就是，集合本身是第二类集合相矛盾！

那么，就再次假设它属于第一类，既然它属于第一类，所以它也一定满足第一类的特征，就是它本身存在于它的子集中（是它其中的某一个集合元素),根据定义它的元素都是第二类集合，它属于它其中的某个元素，也就表示它是第二类集合，这样又与题设发生了矛盾.

　　　　　　　　　　　　　　

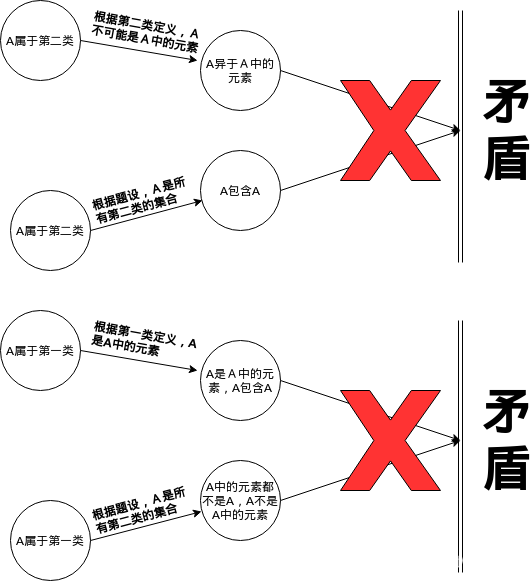
总之，这是个无解的问题！要不怎么叫做悖论呢?

更通俗的提法可以看理发师悖论，理发师悖论突出了本质，但是缺少了理论说明和推导，这里用集合论的方法理解，可以映射到理发师悖论的理解上。

理发师悖论的内容是，很早以前的一个村庄里，只有一个理发师，他规定只给而且一定给不给自己理发的人理发，这就引出了一个问题，“他该不该给自己理发？”

如果他给自己理发，那它就是给自己理发的人，按道理他就不应该给自己理发，可是如果他不给自己理发，那他就属于不给自己理发的人，所以他就应该要给自己理发。

这样，无论从哪个前提开始，都推出了这个前提的否命题，根据排中律，命题和否命题只能有一个成立，不可能同时成立，形成悖论。

上面是通俗理解，用集合论的观点来分析

  设A={x|x表示这个村子所有可以自己给自己理发的人}

  设B={y|y表示这个村子里不能自己给自己理发的人}

  C={理发师｜这个村子唯一一个理发师，而且只给集合Ｂ的人理发}

C是一个理发师，他只给不能给自己理发的人理发。

那么C属于Ａ还是属于Ｂ呢？

如果Ｃ属于A, 那么C不应该属于A, 如果C属于B，又会推出C不属于B.

这个理发师真纠结!