一位名人曾经说过,所谓教育,是忘却了在学校学得的全部内容之后剩下的本领。这句话让人联想到金庸小说倚天屠龙记中的一段情节,张三丰训练张无忌太极拳法对战玄冥二老,在传授完后,询问张无忌学的如何,回答忘记一小部分,张摇摇头,认为尚无取胜把握,要求继续练,训练后再问,张无忌回答已经忘记一大部分了,张三丰逐渐面露喜色,要求继续练,最终,张无忌把教它的东西全部都忘记了,张三丰获悉非常高兴,说你可以去和他们打了。
1.给儿子买了一套数字华容道的棋盘,结果毫不意外地成了我打发时间的工具,玩儿多了后就有了一些心得,结合网上的资料,总结如下图所示。

这是一个NPC问题,目前还没有通用解法。更深刻的数学原理涉及到群论了,群论在大学数学里面有着完全不一样的画风,没有深入学习过。不过,可解条件中之所以要考虑空格行数,并且奇列和偶数列考虑情况不同,这是由于,对于奇列的情况,空格的上下调整不改变排序逆序数的奇偶性,但是偶数列显然不不是,空格上下移动,你叙数的奇偶性会发生变化。奇会变成偶,偶会变成奇。

以上面3阶为例,列为奇数,从上面的置换变为下面的置换,可以通过两次交换得到,分别是
每次交换,数列均会改变奇偶性,经过两次交换后,奇偶性不变。
但是对于四阶就不同了,对四阶来说,空格上下移动时,相当于进行连续的三次交换,移动后的序列奇偶性会翻转。
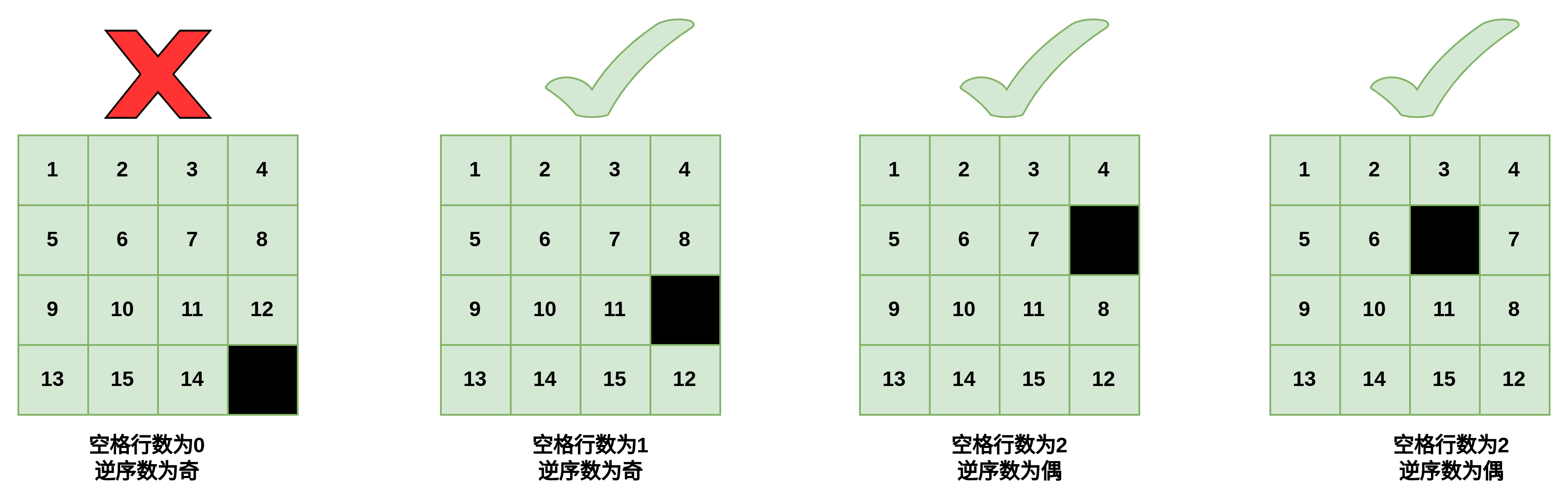
水平移动不影响奇偶性和空格行数。
以三阶为例,可以验证,每个复原步骤均满足上述条件:

共计48步,这个步数必定是个偶数,因为黑框从最后一个位置再回到最后的位置,必定为偶数,根据群的基本理论,所以必须保证初始状态的逆序数也为偶数。这样完成后才满足偶置换的要求,如上列出的所有条件都是为了满足这个要求。
写了一个深搜程序,计算出来四种方案,步骤都非常多,可见如果想得到最优补数需要用到广搜,深搜一头走到黑,得到的一般不是最优结果,如果限制路径堆栈的深度,可以得到接近最优的搜索路径:

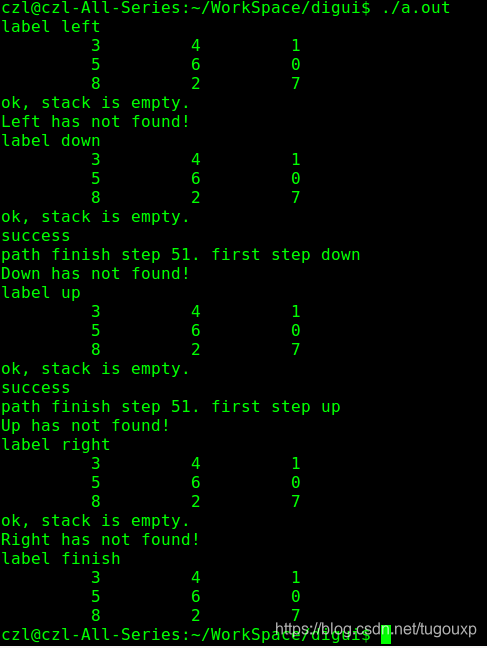
限定步骤前后,之所以产生如此大的差异,是由于深度搜索过程中,首次出现的某个可解状态并非以最优次序出现,导致即便后续最优序列出现的时候,由于状态重复而被剪枝
2.为什么正多面体的种类是有限的?你可以这样想:
0.三维空间中的多面体至少要有四个面,所以不可能出现正三面体,正二面体,甚至是1面体
1.要形成某种顶点或者“尖顶",在多面体的任何顶点至少要有三个多边形的面必须相交.
2.由于多面体是规则的,因此在任意顶点的情形与在任意其它顶点情形相同,因此,我们只需要考虑在一个典型的顶点上发生的情况。
3.为了要形成一个尖顶,顶点上所有面角之和必须小于360度,也就是说,围绕一个定点的所有的角相加之和必须小于一个周角,反证法,如果不满足,则这些角加起来将会形成一个平面。
4.因为所有的面都是全等的,所以一个顶点上所有角的和必须被均分
5.设正多边形内角和为e, 则
e = (n-2)*180, n为边
正多边形每个内角均相等,所以
y = e/n = ((n-2)/n) *180
此函数图像是:

可以看到,正六边形的每个内角是120度,已经不满足要求,而函数图形是增函数,所以:
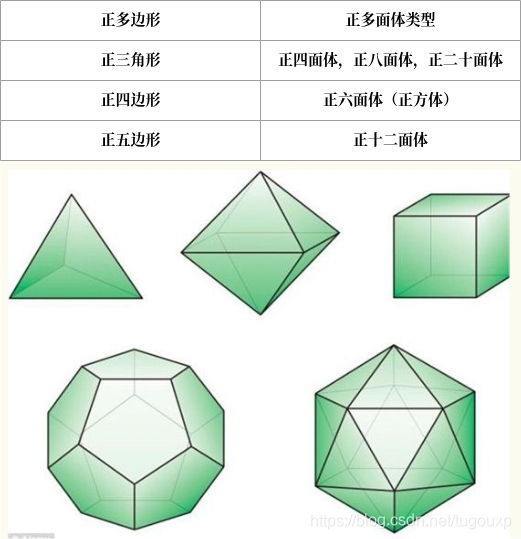
能够组成正多面体的正多边形只能是边数小于6的正多边形.
正三角形
正四边形
正五边形
三种,五种柏拉图正多面体恰好是由这三种面组成的。

总结一下,由于要构成一个顶点需要的面至少是三个,这是构成顶点面的下界,对应每个多边形内角为60度,随着边数的增加,内角也逐渐增加,但是,每个多边形的内角不能大于等于120度,对应了正六边形,限制了构造正多面体面的边数不能多于5个边.并且小于一定边数的正多边形也是有限的为3,内角也不能无限小,最小只能到60度,所以构成顶点的面及不能太小(下界3),又不能太大,不能超过5个,这是上界,这么多的限制,当然体数有限了.

3.三角和函数的几何证明以及它与矩阵变换以及复数旋转的联系
cos(a+b) = cos(a)cos(b) - sin(a)sin(b)
sin(a+b) = sin(a)cos(b) + cos(a)sin(b)
旋转矩阵:
cos(a) -sin(a)
sin(a) cos(a)
可以用上面的矩阵左乘一个向量去验证.
引用对角线法则,变换矩阵在空间中的伸展长度是1,另外需要注意的是,对角线法则只适用于1,2,3阶矩阵,1阶矩阵即标量常数。
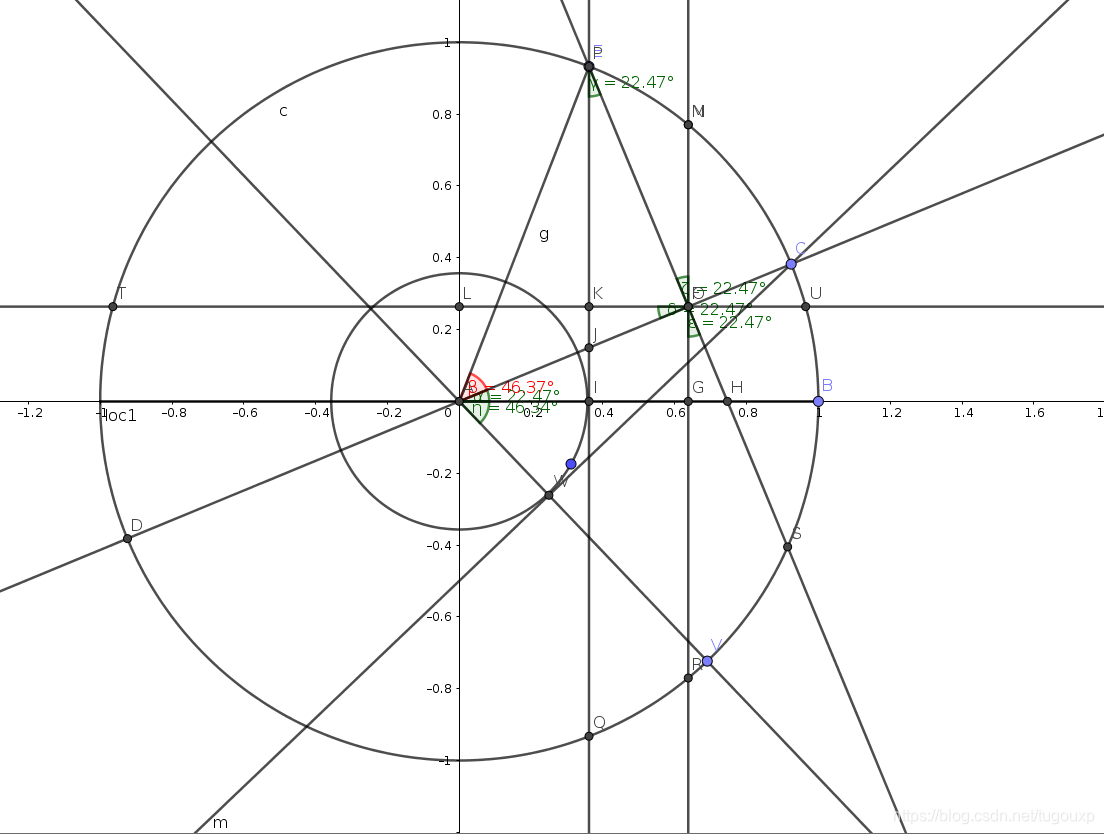
还可以从另一个角度理解,这也是在看了3blue1brown的视频受启发想到的,大学学习线性变换中的基都是按照列向量来定义的,但线性代数中的大部分定理都同时适用于行向量和列向量,隐隐觉得这里面应该有一些对称的东西没有挖掘出来,看了视频讲duality,翻译过来恰好是对偶性,这个解释就不从列向量的角度来理解,而从行向量的角度理解这个变换.
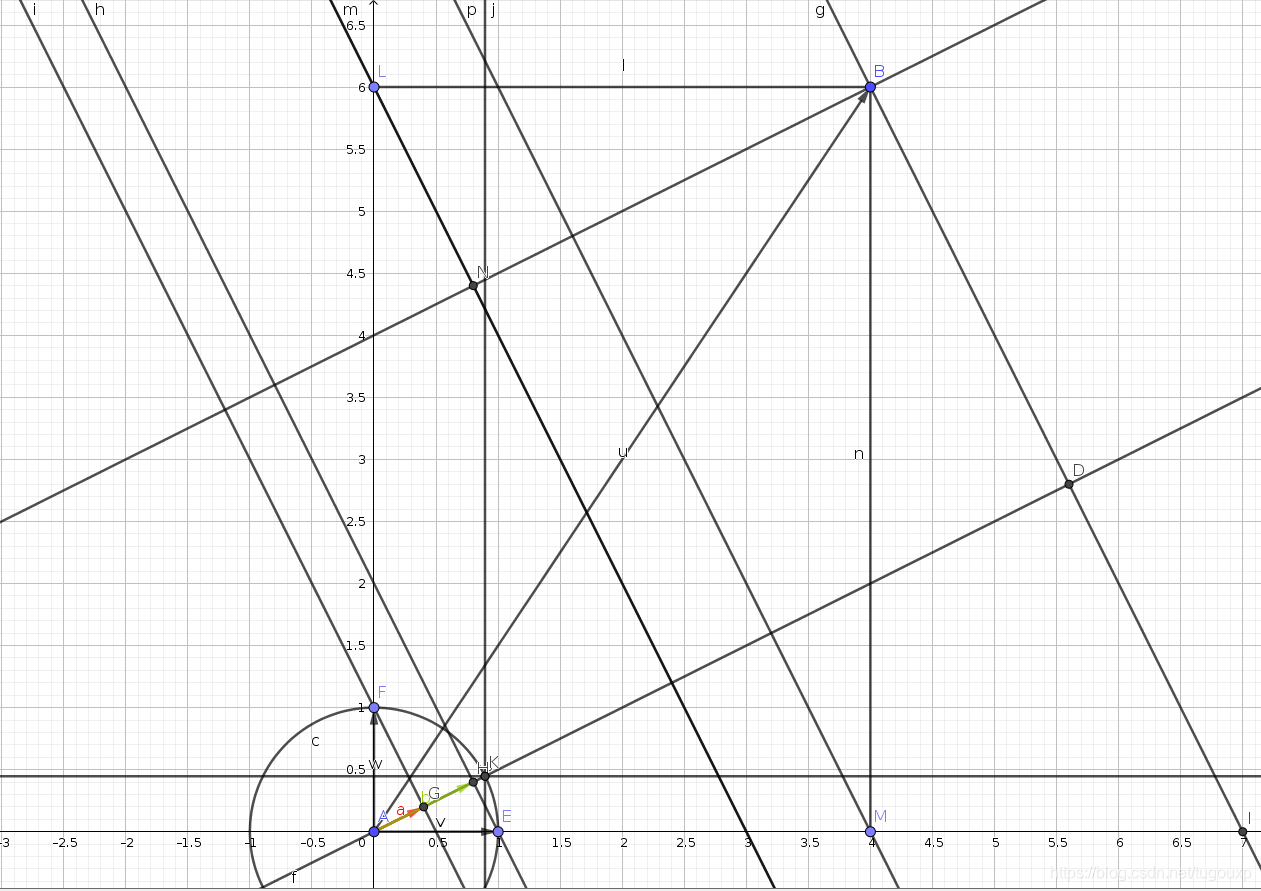
首先,旋转矩阵的行向量[cos(beta), -sin(beta)],乍看一下好像没有什么意义,但是当我们从原点A做一个向量,使它的角度恰好等于beta,也就是上图中的yita(没找到办法绘制一个和给定角度一模一样的角度的办法,差不多就行了,能说明问题).也就是angle(VOB),原点是O.
这里,如果把[cos(beta), -sin(beta)]看做是正交向量(1,0)和(0,1),也就是坐标轴,做线性变换将维成1维线而得的话,那么
cos(beta)*cos(a) - sin(beta)sin(a)就可以理解为向量OC在直线上的投影,也就是OW,那么他就应该等于根据上面几何证明的旋转后的横坐标值OI,直观上,I点和W点应该在以原点为圆心的某个圆上,虽然上面绘制的角度有误差,可是看到实际上确实如此,
I和W几乎和同一个圆相切(实际上就是在圆上,代数证明的手艺早就还给老师了,还是看图说话吧,毕竟年纪大了,很多理论的东西有直观的解释最好).
所以,行向量的几何意义可以解释为,基向量在行向量方向上的投影长度,也就是基向量坍缩到某个一维方向后,各基的投影长度,如果知道一个点的坐标,则变换后的坐标就是坐标值在每个方向的投影长度的贡献之和,用公式表达就是内积了。
利用向量内积的观点,可以解释x+y+z=0的图形为什么是个平面,因为所有x,y,z是满足所有与(1,1,1)点积为0的点组成的集合
从几何直观上看就是个平面了. :)
红色,绿色和蓝色分别为x,y,z轴


4.加减运算和数乘运算我们一般称之为线性运算,线性运算是整个空间理论的基础,为了计算的方便,可以把向量放到坐标系中来研究,因为向量可以平移,并且平移后向量保持不变,我们把所有向量的起点都平移到坐标原点,这样
就可以用终点坐标来表示向量,所以,平面上所有向量的终点就铺满了整个平面,平面就可以看成所有二维向量的集合,所以研究三维空间,四维空间乃至高维空间,都是向量的集合,三维空间就是所有三维向量的集合,四维空间就是所有四维向量的集合,n维空间就是所有n维向量的集合。n维向量又是什么?2维向量就是有两个坐标的数列,三维向量有三个坐标的数列,n维向量自然就有n个坐标了。这是巧合吗?当然不是的,因为我们就是用基的向量个数来表示向量维度的,而基的个数又需要有对应的坐标来描述,所以我们定义,一个n个实数排列在一起组成的有序串,就称为一个实数域上的n维向量。记做:
![\vec{x}=[x_1,x_2,x_3,\cdots,x_n]](https://i-blog.csdnimg.cn/blog_migrate/646c56449715c44311e8988dba303cb3.gif)
横着写称为行向量,竖着写称为列向量, 本质上行向量和列向量是一样的。
关于线性变换,体会动态的变换过程,比线性代数中的讲解直观多了。
(1, 3) + (-3, 2) = (-2, 5)
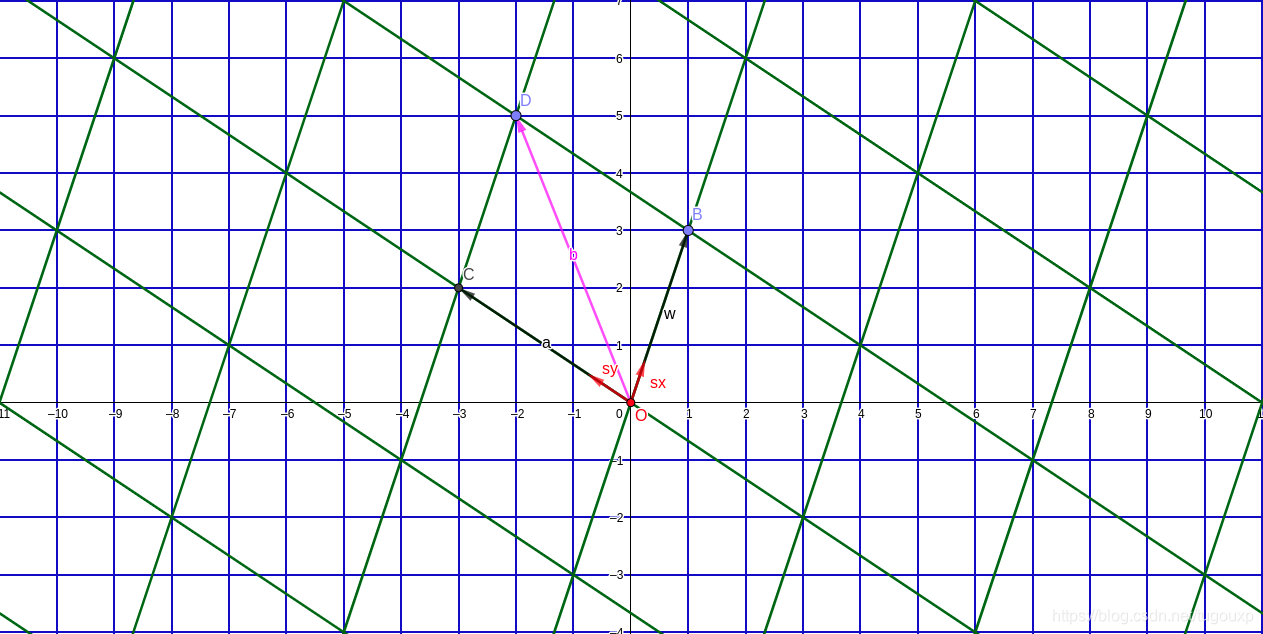
上图中有两个坐标世界,A世界的坐标轴即是普通直角坐标轴,单位坐标矩阵是:
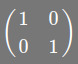
世界B的单位坐标轴,在世界A中的坐标矩阵是:

如果世界A中有一点D,在世界A中的坐标是

,那如果我想得到D点用B世界的坐标轴表示的坐标,该如何表示呢?
可以这样想,B世界的坐标是怎么来的?可以看作是A世界的两个直角坐标轴经过旋转和缩放得到的,
也就是OB向量是由x轴单位向量旋转得到, OC由y轴单位向量旋转得到.
在坐标系内,旋转对应一个线性变换矩阵(其实这个矩阵就是B世界在A世界中表示的坐标,也就是上面第二个矩阵),一个线性变换的衡等式,在变换前后应该保持不表,所以,变换前后,D点在A世界中的坐标表示和在B世界中的坐标表示应该是相同的,所以只要算出D点变换前在A世界的坐标,这个坐标也就是用新向量表示的坐标了.
所以,距离结论,我们差着一个逆变换,这也就是求矩阵的逆矩阵:
 X
X  =
= 
所以  = InverseMatrix(
= InverseMatrix( ) X
) X  =
=  X
X  =
= ![]()
上面的式子实际上是在说,在坐标系 下的向量
下的向量![]() ,与在E单位矩阵坐标系下的向量)
,与在E单位矩阵坐标系下的向量) ,实际上是同一个向量.
,实际上是同一个向量.
线性变换的一个重要性质在于,变换后的向量仍然是相同的线性组合,不过使用的是新的基向量,比如这里变换前的 (1,1)向量和变换后的(-2,5)向量在各自坐标系中的坐标都是(1,1),但却换了一组基.
对于常见的多元线性方程组,可以书写为矩阵和向量乘积的形式。

其简单而直观的几何意义就是,矩阵A表示了一种线性变换,现在空间中得到一个向量![]() ,使其在执行完线性变换后,和
,使其在执行完线性变换后,和![]() 重合。
重合。
以上例子,就是逆矩阵简单的几何意义
5.二阶行列式等于向量包围平面面积的几何证明
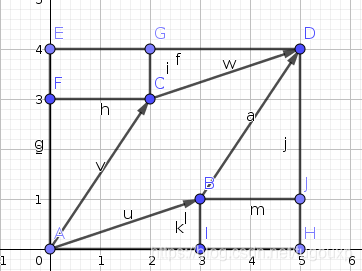
C点的坐标(a,b), b点的坐标是(c,d)
二阶行列式
[c, a]
[d, b]
则为bc - ad.
几何证明方式,中间平行四边形的面积是:
(a+c) * (b+d) - a*d - a*d - 1/2(a*b) - 1/2(a*b) - 1/2(c*d) - 1/2(c*d)
= bc-ad
QED.
6.向量内积为何是一条向量投影长度和另一条向量长度乘积的几何解释.,
6.矩阵行秩等于列秩的直观解释,两个平行四边形张开的维度时时刻刻都保持相同.
说白了,有几个方向(坐标轴,方程个数)就需要有一个变量来描述各个方向的标量值.

代数证明:
假设m*n阶矩阵A的列秩为c,行秩为r。则A包含c个m维线性独立的列向量,它们张成A的列空间。将这些列向量放到一起组成一 个mxc阶矩阵B

则A的每一个列向量

均可以唯一的表示成b的列向量![]() 的线性组合.
的线性组合.

所以,

考虑矩阵A的第i行,利用以行为计算单元的矩阵乘法规则,可得,
 矩阵A的每一行可以表示成D的每一行的线性组合,因为A的行空间维数不大于D的行数,因此,行秩r小于等于c,即A的行空间维数不大于列空间维数。
矩阵A的每一行可以表示成D的每一行的线性组合,因为A的行空间维数不大于D的行数,因此,行秩r小于等于c,即A的行空间维数不大于列空间维数。
同理,可得到转置后的r>=c.
所以只能r=c.
7.当要解决的问题符合以下三条,可以考虑运用机器学习:
-
要解决的问题中存在某种模式
-
这种模式不容易直接定义
-
有足够的数据可以帮助我们找出该模式
8.自然常数(欧拉数)的产生函数

8:在书上看到这样一段话特别有感悟,数学可能是最接近哲学的一门学科了.
原话(爱因斯坦语): "在这里产生了一个让各个时期的科学家都困惑的谜题,数学作为独立与经验的人类思维的产物,为何与物理现实中的客体如此吻合?没有经验依据,而只靠纯粹思维,人类就能够发现实际事务的性质吗?......
只要数学的命题是涉及实在的,他就是不可靠的;只要它是可靠的,他就不涉及实在."
或则和简单论述为,数学法则只要与现实有关,都是不确定的,若是确定的,都于现实无关。
大家的思维就是不一样,比如通常认为的根号2为无理数,如果想在自然界中证明,通过度量正方形的对角线和边之比来证明论断的正确性,是根本不可能的,自然界中的对象没有理想的精确形式,所以这个结论不能从直接的度量中绝对精确的的出来,也不能对任何一个具体的现实正方形有绝对精确的意义.
量的精确化超过一定限度,总要产生质的变化,比如,气压如果精确到超过一个分子的撞击力大小时,是没有意义的,当电量描述超过个一个电子所带电荷的程度时,是没有意义的,所以,对于数学中的理论证明,要通过纯粹的逻辑推导和形式化的思辨才能达到.
这就是为什么数学结论可以脱离实验的证明,仍然会被人们所信服.
我们学习知识有一个回顾和反思的过程,很遗憾毕业十年后才感受到数学的美感,用心去体会而不是为了应付考试,如果你喜欢统一喜欢对称,喜欢数学繁杂表象背后都有简单而统一的运行机制,在毕业多年后,再回头重温一下,这样便于我对问题的理解,也便于产生新的思考.
9:下面是一个非常著名的函数图形,魏尔斯特拉斯函数,它的特征是处处连续,但却处处不可导,翻译成人话就是你无法用笔画出它其中的哪怕任何片段,因为人的手臂是有质量的,有质量的物体动起来是有惯性的,惯性携带了趋势信息,而这个函数图像不带有任何趋势信息,也就是你看不出任何微观上的走势,就是这么任性,现实中或许只有股票走势曲线能和它媲美了,是不是很神奇?如果牛顿和莱布尼兹两位神仙知道有这类函数的存在,不知道还能不能发明微积分 :). 不过,在数学创造中,自由创造会领先于形式化和逻辑基础.这类函数还有很多,因为不能用初等函数的解析式来表达,被称为病态函数,实际上,就像宇宙中的暗物质远远多于普通物质一样,病态函数的数量要远远多于基本初等函数的变换形式,这个世界的本质是病态的.

matlab源码:
%x = linspace(-2,2);
x = -2:.000004:2;
%a = 1/4;
%b = 51;
a = 1/2;
b = 3;
y = zeros(length(x),5);
[row, col] = size(y);
Y = zeros(size(x));
for i = 1:length(x)
for j = 1:col
y(i,j) = (a^(j-1))*cos((b^(j-1))*pi*x(i));
end
Y(i) = sum(y(i,:));
end
plot(x,Y)
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
function weierstrass(a,b,kmax)
% WEIERSTRASS Plots Weierstrass's non-differentiable function for
% the interval [0,1].
%
% w(x) = sum_{k=0}^{\infty} a^k \cos(2\pi b^k x)
% with 0 < a < 1 and a*b >= 1
%
% Funktion arguments:
% a, b : Coefficients (default: a=0.5, b=3)
% k : upper limit of k for the computed sum (default:
% k=20)
% Author : Andreas Klimke, Universität Stuttgart
% Version : 1.0
% Date : August 12, 2002
if nargin~=3
if nargin<2
a = 0.5;
b = 3;
end
kmax = 20;
end
c1(1:kmax+1) = a.^(0:kmax);
c2(1:kmax+1) = 2*pi*b.^(0:kmax);
x = linspace(-2,2,1000000);
plot(x,w(x,c1,c2),'b-','LineWidth',2);
title('Weierstrass''s non-differentiable function','Fontsize',18);
xlabel(['a=' num2str(a), ', b=' num2str(b)],'Fontsize',16);
ylabel('w(x) = sum_{k=0}^\infty [a^k cos(2 \pi b^k x)]','Fontsize', ...
16);
set(gca,'FontSize',14);
grid on;
%--------------------------------
function y = w(x,c1,c2)
index = 1;
y = zeros(length(x),1);
for k = x
y(index) = sum(c1 .* cos(c2*k));
index = index + 1;
end9:究竟反比函数是不是双曲线?图形化证明一下:
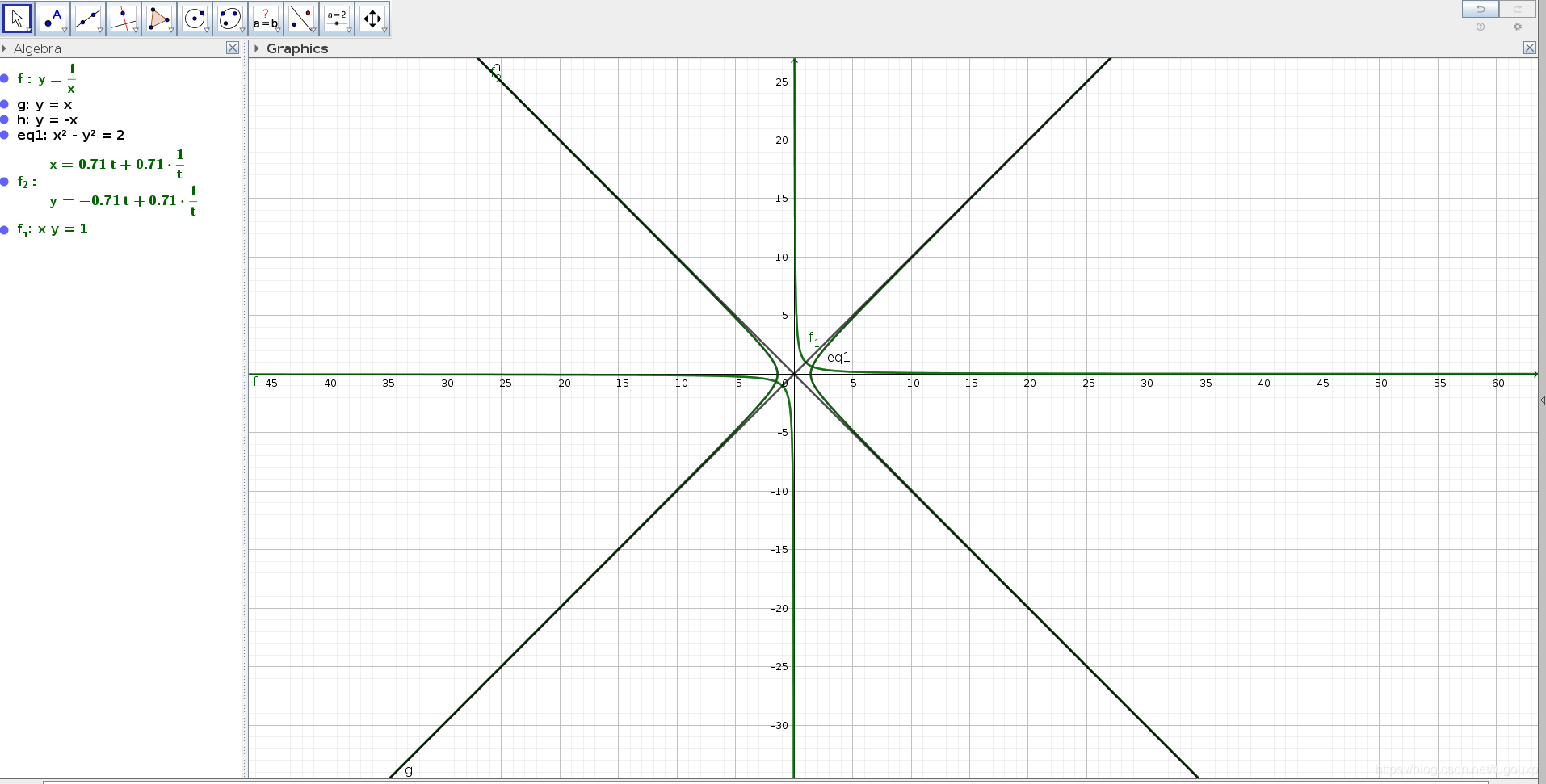
从图中可以看到,函数f1是反比函数,函数eq1是关于x轴对称的双曲线函数,离心力为根号2,渐近线是y=x以及y=-x.
根据geogebra计算后绘制的结果,无论是f1逆时针旋转45度,还是eq1顺时针旋转45度,都和目的图形完全重合,所以看起来反比函数确实是如假包换的双曲线。
我们也可以代数证明一下这个结论,利用坐标线性变换的概念.
假设坐标轴顺时针旋转45度角后,新的坐标系坐标是(x^, y^);
则在原坐标系中的坐标位置应该等于旋转矩阵

两个列向量的有限次线性变换得到,具体一点就是如下算是
 *
*  =
= 
所以 xy = 1
推导出

坐标转换关系式:
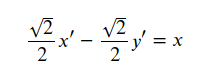

简化后实际上是

明显是双曲线的方程。
所以可以得出,反比函数是如假包换的双曲线,并且更一般的,
![]() 和
和 ![]() 描述的是同样形状的双曲线,只是观察他们的坐标系的角度不同。
描述的是同样形状的双曲线,只是观察他们的坐标系的角度不同。
扩展到三维场景,z=xy本质上也是马鞍面和

具有同样的形状,只是旋转了45度而已.
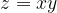



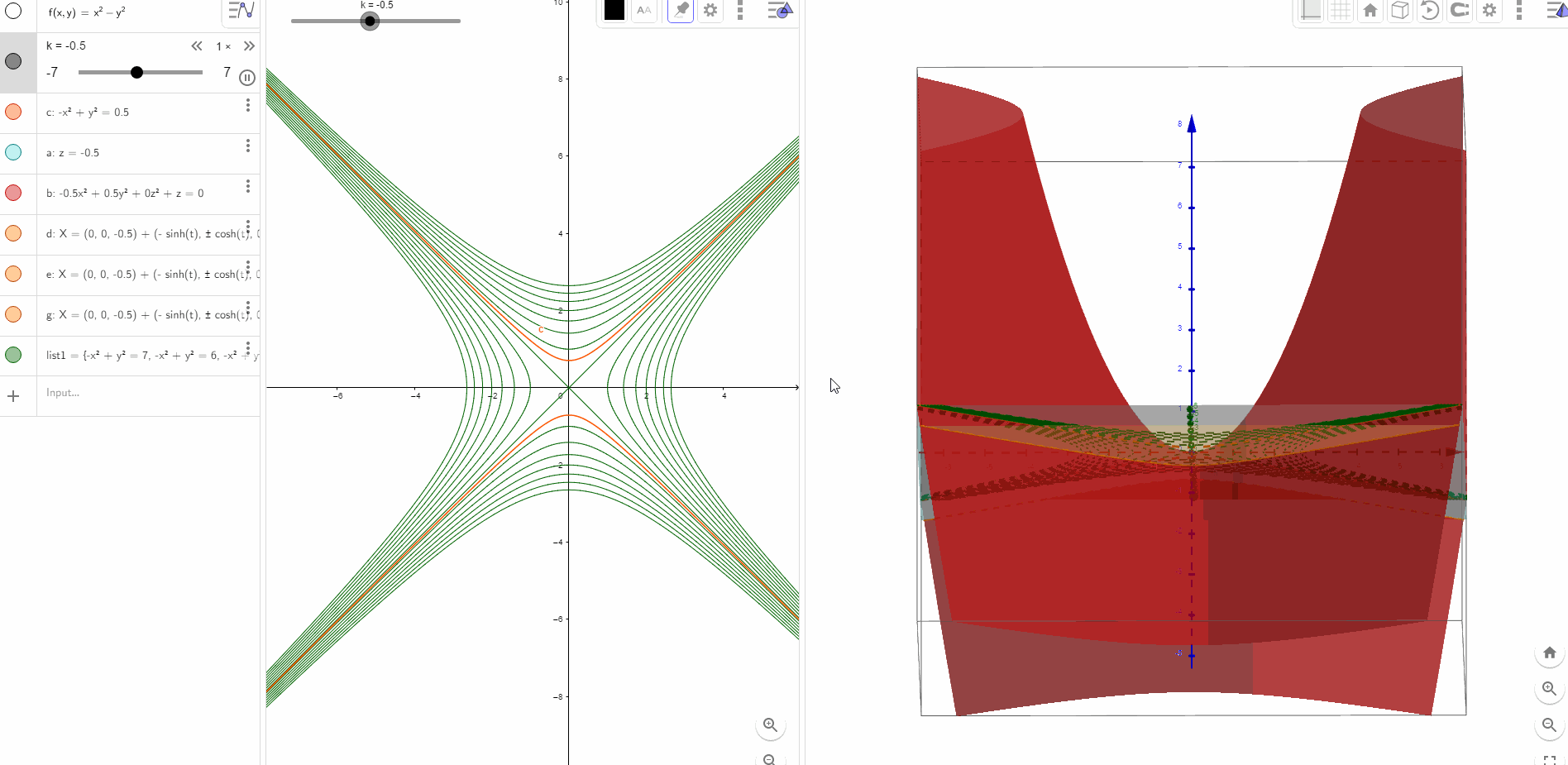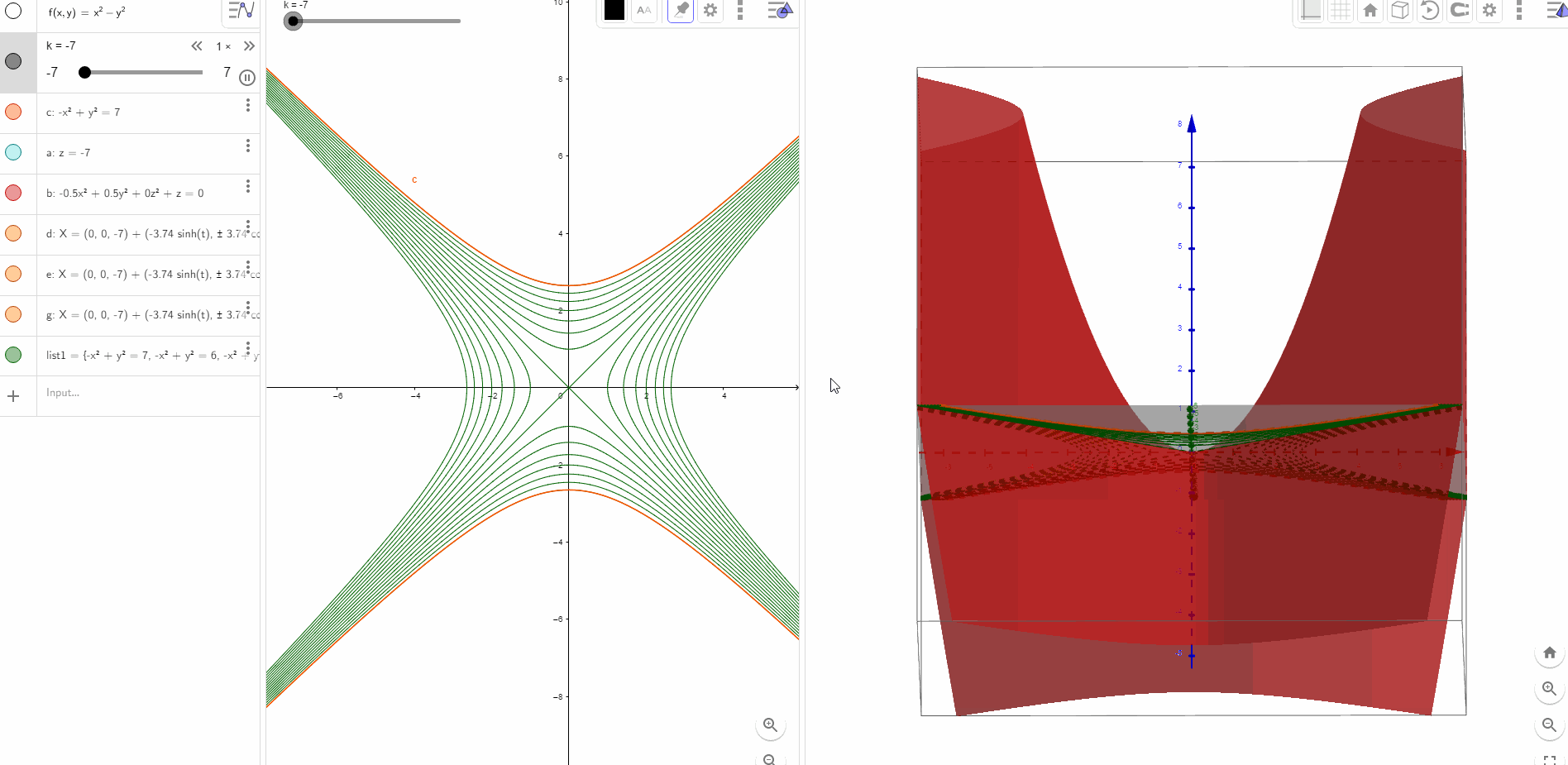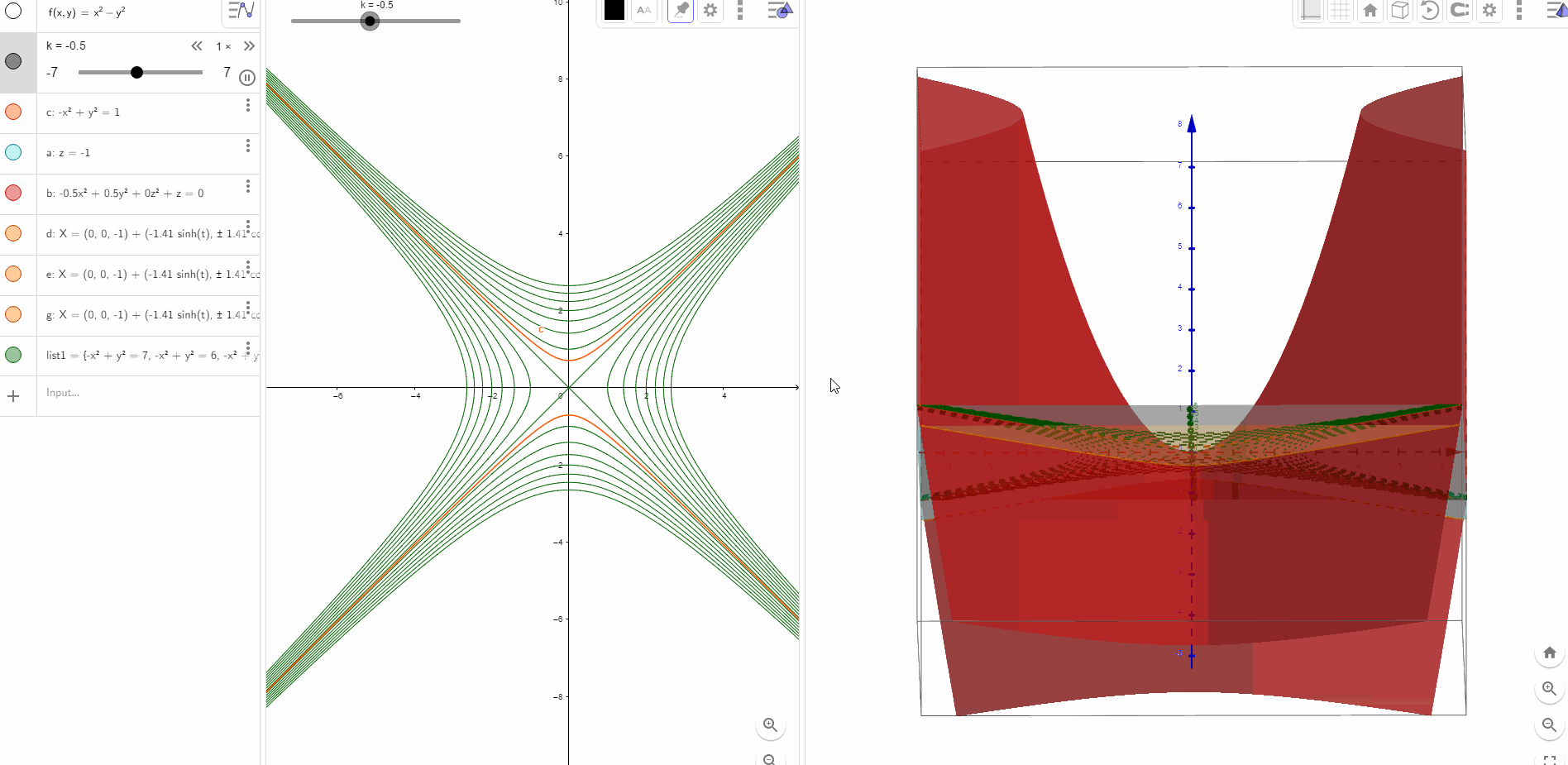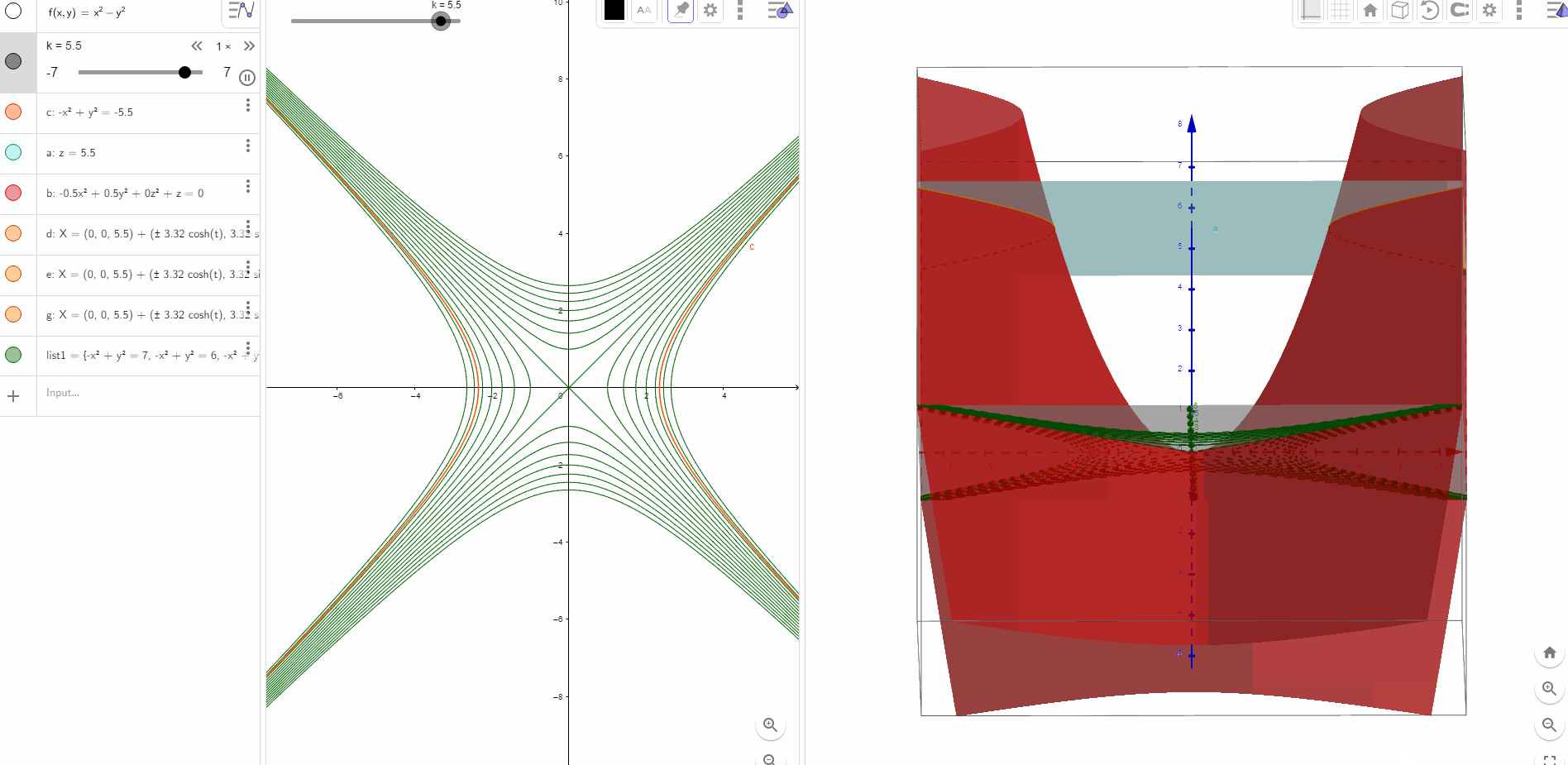
图形是一个标准马鞍面.等高线是一组组的双曲线,反比函数的双曲线是其中一组。
也可以用二次型的概念来解释这个问题,二次型是二次齐次多项式

符合二次型的定义,对应的对称方阵为:
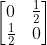
对应的转换矩阵和二次型矩阵是:

所以 变换矩阵为:
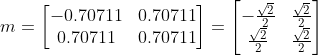
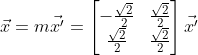
所以:
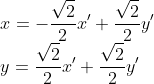
所以
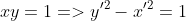
所以,二次型的方式也可以得到正确的结论.
扩展到复数域,复变函数
 c为复变量.
c为复变量.
的图像在实数域是由两张一样的马鞍面张开的。
设:
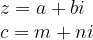
所以

进而得到:
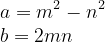
根据上面的的分析结果,
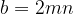 和
和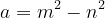
是同样的双曲线,只是相差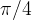 角度
角度
:

matlab中可以将四维变元在同一张图中显示出来,方法是xoy平面表示自变量所在的复平面,以z轴表示复变函数的实部,颜色表示复变函数的虚部,如下面第一张图。

10:一个非常有意思的函数图形,y=x^2*sin(1/x),它处处可导,但是导函数在x=0处却不连续,也就是存在可导,但是导函数却不连续的函数,而且这个函数比较奇怪的是,在微观上和宏观上完全不像,微观上渐近线是二次函数y=正负x^2,宏观上的渐近线是y=正负x.
进一步分析,函数
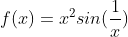
仅仅在x=0点没有定义,所以,可以抛弃原来的定义,重新定义 如下:
如下:
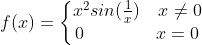
不过由于
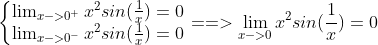
所以尽管f(0)没有定义,但是将定义转换为如上的函数后,f扩展为连续函数.
再 处,f(x)的导数是:
处,f(x)的导数是:
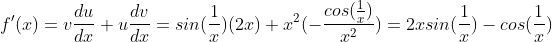
在x=0处的导数,没有法则可以帮忙,只能根据定义来计算:
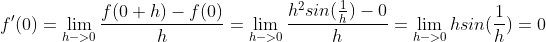
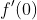 存在并且为0,意味着f实际上再x=0处可导.
存在并且为0,意味着f实际上再x=0处可导.
所以
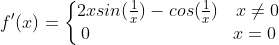
有意思的是:
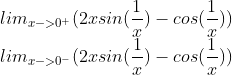
并不存在,所以
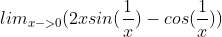
不存在,
所以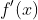 不连续!
不连续!
所以对于f(x)来说,它是一个处处可导的函数,但是其导函数在x=0处有间断点,并不连续,可惜的是,根据实数的性质,是





 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章


















 861
861












