图像保边滤波器集锦---双边滤波算法与实现

双边滤波算法

算法定义与流程：

#include "string.h"
#include "stdio.h"
#include "stdlib.h"
#include "math.h"
#include"SoftSkin.h"



//垂直方向递归
void runVerticalHorizontal(double *data,int width,int height,double spatialDecay,double *exp_table,double *g_table)
{
	int length0=height*width;
	double* g= new double[length0];
	int m = 0;
	for (int k2 = 0;k2<height;++k2)
	{
		int n = k2;
		for (int k1 = 0;k1<width;++k1)
		{
			g[n]=data[m++];
			n += height;
		}
	}
	double*p = new double[length0];
	double*r = new double[length0];
	memcpy(p, g, sizeof(double) * length0);
	memcpy(r, g, sizeof(double) * length0);
	for (int k1 = 0;k1<width; ++k1)
	{
		int startIndex=k1 * height;
		double mu = 0.0;
		for (int k=startIndex+1,K =startIndex+height;k<K;++k)
		{
			int div0=fabs(p[k]-p[k-1]);
			mu =exp_table[div0];
			p[k] = p[k - 1] * mu + p[k] * (1.0 - mu);//文献中的公式1，这里做了一下修改，效果影响不大
		}
		for (int k =startIndex+height-2;startIndex <= k;--k)
		{
			int div0=fabs(r[k]-r[k+1]);
			mu =exp_table[div0];
			r[k] = r[k+1] * mu + r[k] * (1.0-mu) ;//文献公式3
		}
	}
	double rho0=1.0/(2-spatialDecay);
	for (int k = 0;k <length0;++k)
	{
		r[k]= (r[k]+p[k])*rho0-g_table[(int)g[k]];
	}
	m = 0;
	for (int k1=0;k1<width;++k1)
	{
		int n = k1;
		for (int k2 =0;k2<height;++k2)
		{
			data[n] = r[m++];
			n += width;
		}
	}
	memcpy(p,data, sizeof(double) * length0);
	memcpy(r,data, sizeof(double) * length0);
	for (int k2 = 0; k2<height;++k2)
	{

		int startIndex=k2 * width;
		double mu = 0.0;
		for (int k=startIndex+1, K=startIndex+width;k<K;++k)
		{
			int div0=fabs(p[k]-p[k-1]);
			mu =exp_table[div0];
			p[k] = p[k - 1] * mu + p[k] * (1.0 - mu);
		}
		for (int k=startIndex+width-2;startIndex<=k;--k)
		{
			int div0=fabs(r[k]-r[k+1]);
			mu =exp_table[div0];
			r[k] = r[k + 1] * mu + r[k] * (1.0 - mu) ;
		}
	}

	double init_gain_mu=spatialDecay/(2-spatialDecay);
	for (int k = 0; k <length0; k++)
	{
		data[k]=(p[k]+r[k])*rho0-data[k]*init_gain_mu;//文献中的公式5
	}
	delete p;
	delete r;
	delete g;
}
//水平方向递归
void runHorizontalVertical(double *data,int width,int height,double spatialDecay,double *exptable,double *g_table)
{
	int length=width*height;
	double* g = new double[length];
	double* p = new double[length];
	double* r = new double[length];
	memcpy(p,data, sizeof(double) * length);
	memcpy(r,data, sizeof(double) * length);
	double rho0=1.0/(2-spatialDecay);
	for (int k2 = 0;k2 < height;++k2)
	{
		int startIndex=k2 * width;
		for (int k=startIndex+1,K=startIndex+width;k<K;++k)
		{
			int div0=fabs(p[k]-p[k-1]);
			double mu =exptable[div0];
			p[k] = p[k - 1] * mu + p[k] * (1.0 - mu);//文献公式1

		}
		for (int k =startIndex + width - 2;startIndex <= k;--k)
		{
			int div0=fabs(r[k]-r[k+1]);
			double mu =exptable[div0];
			r[k] = r[k + 1] * mu + r[k] * (1.0 - mu);//文献公式3
		}
		for (int k =startIndex,K=startIndex+width;k<K;k++)
		{
			r[k]=(r[k]+p[k])*rho0- g_table[(int)data[k]];
		}
	}
	
	int m = 0;
	for (int k2=0;k2<height;k2++)
	{
		int n = k2;
		for (int k1=0;k1<width;k1++)
		{
			g[n] = r[m++];
			n += height;
		}
	}
	memcpy(p, g, sizeof(double) * height * width);
	memcpy(r, g, sizeof(double) * height * width);
	for (int k1=0;k1<width;++k1)
	{
		int startIndex=k1 * height;
		double mu = 0.0;
		for (int k =startIndex+1,K =startIndex+height;k<K;++k)
		{
			int div0=fabs(p[k]-p[k-1]);
			mu =exptable[div0];
			p[k] = p[k - 1] * mu + p[k] * (1.0 - mu);
		}
		for (int k=startIndex+height-2;startIndex<=k;--k)
		{
			int div0=fabs(r[k]-r[k+1]);
			mu =exptable[div0];
			r[k] = r[k + 1] * mu + r[k] * (1.0 - mu);
		}
	}

	double init_gain_mu=spatialDecay/(2-spatialDecay);
	for (int k = 0;k <length;++k)
	{
		r[k]= (r[k]+p[k])*rho0- g[k]*init_gain_mu;
	}
	m = 0;
	for (int k1=0;k1<width;++k1)
	{
		int n = k1;
		for (int k2=0;k2<height;++k2)
		{
			data[n]=r[m++];
			n += width;
		}
	}
	delete p;
	delete r;
	delete g;
}

void ApplyBiExponentialEdgePreservingSmoother(double photometricStandardDeviation, double spatialDecay, unsigned char* m_pImage, int  m_nWidth, int m_nHeight,int m_nStride)
{
	double m_exp_table[256];
	double m_g_table[256];
	memset(m_exp_table, 0, 256);
	memset(m_g_table, 0, 256);
	double c=-0.5/(photometricStandardDeviation * photometricStandardDeviation);
	double mu=spatialDecay/(2-spatialDecay);
	for (int i=0;i<=255;i++)
	{
		float a=exp(c*i*i);
		m_exp_table[i]=(1-spatialDecay)* exp(c*i*i);
		m_g_table[i]=mu*i;
	}
	unsigned char* p0 =m_pImage;
	const int nChannel = 4;
	int m_length =m_nWidth*m_nHeight;
	float maxerror=0;
	float sum=0;
	// 对每个channel进行处理

	for (int idxChannel=0;idxChannel <nChannel; idxChannel++)
	{
		double *data1 = new double[m_length];
		double* data2 = new double[m_length];

		unsigned char *p1=p0+idxChannel;
		for (int i = 0; i < m_length;++i)
		{
			data1[i] = p1[i * nChannel];
		}
		memcpy(data2,data1, sizeof(double) * m_length);

		runHorizontalVertical(data1, m_nWidth, m_nHeight,spatialDecay,m_exp_table,m_g_table);
		runVerticalHorizontal(data2, m_nWidth, m_nHeight,spatialDecay,m_exp_table,m_g_table);
		sum=0;
	    for (int i =0;i<m_length;++i)
	    {
			double val=(data1[i] + data2[i]) * 0.5;

		    if(255.0<val)val=255.0;
		    p1[i * nChannel]=(unsigned char)val;
	     }
		delete data1;
		delete data2;
	}
	
}

void f_Bilateralfilter(unsigned char* pImage, int nWidth, int nHeight, int nStride, double std)
{
	if (pImage == NULL || std == 0)
	{
		return;
	}
	ApplyBiExponentialEdgePreservingSmoother(std,std * 0.001,pImage, nWidth, nHeight, nStride);
}

效果如下：

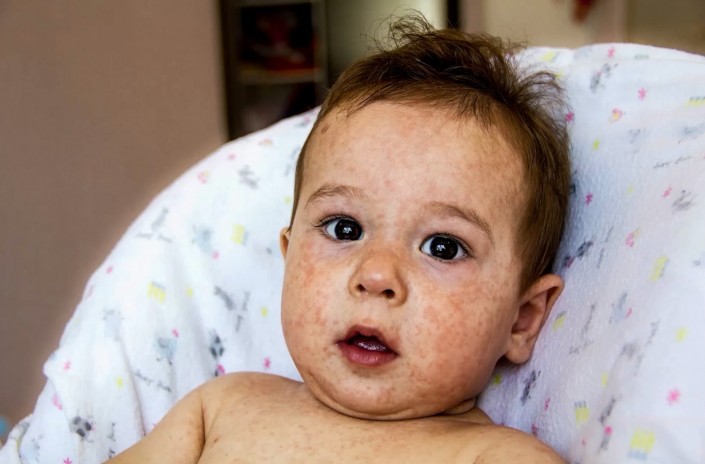
原图

双边滤波效果图(Delta=20)

递归双边滤波是一种快速双边滤波算法，这里本人是对四通道处理的，大家可以在YUV颜色空间对Y通道处理，UV不变，这样速度会更快一些。

完整的DEMO连接：点击打开链接