恒幅值变换和恒功率变换的matlab验证

最新推荐文章于 2025-07-02 10:36:14 发布

原创最新推荐文章于 2025-07-02 10:36:14 发布 · 3.4k 阅读

10 ·

CC 4.0 BY-SA版权

文章标签：

#matlab #Clark #park #电机

电机控制专栏收录该内容

2 篇文章

订阅专栏

本文通过Matlab程序详细验证了Clark和Park变换在电机模型中的应用，包括abc到dq模型的转换过程，以及在恒功率和恒幅值模型下的曲线与幅值对比。通过对变换矩阵的计算，展示了在不同条件下的电流分量变化。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

在matlab中验证clark和park变换后的曲线以及幅值。

关于变换的原理请参考：

https://blog.youkuaiyun.com/chenjianbo88/article/details/53027298

当恒幅值变换时：

程序中 ConAmp = 1，恒幅值输出，iq的幅值和ia幅值相等。

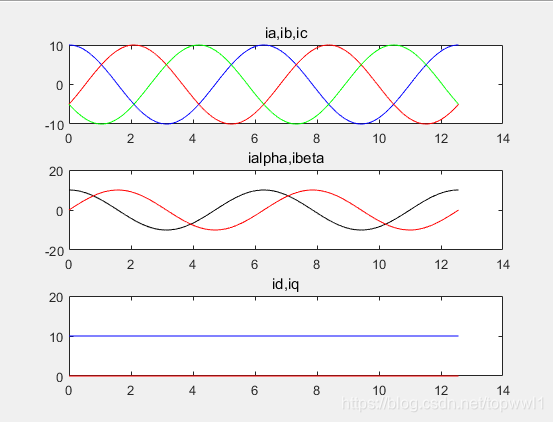
程序中 ConAmp = 0，恒功率输出，iq的幅值和ia幅值相等。

ia = $\sqrt{2/3}$ i_alpha

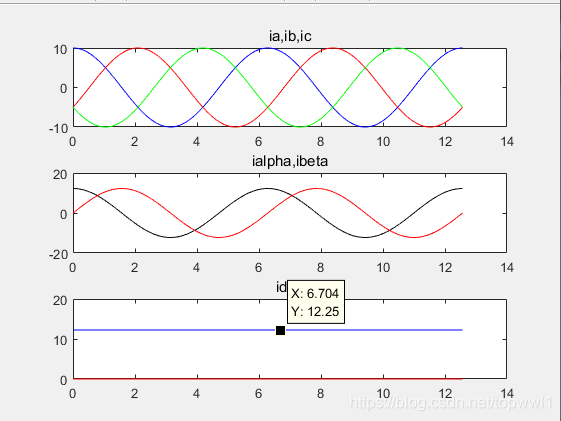
%电机abc模型推导dq模型过程中的公式验证
%恒功率模型，恒幅值模型只需要结果乘以sqrt(2)/sqrt(3)
j = 0;
ConAmp = 0;
for i=0.0:0.001*pi:4*pi
    j = j+1;
    ia(j) = 10 * cos(i);
    ib(j) = 10 * cos(i-2/3*pi);
    ic(j) = 10 * cos(i+2/3*pi);
    
    ConPower_C3sto2s = sqrt(2/3) * [1 -1/2 -1/2; 0 sqrt(3)/2 -sqrt(3)/2];
    ConPower_C2sto3s = sqrt(2/3) * [1 0; -1/2 sqrt(3)/2; -1/2 -sqrt(3)/2];
    a
    ConAmp_C3sto2s = (2/3) * [1 -1/2 -1/2; 0 sqrt(3)/2 -sqrt(3)/2];
    ConAmp_C2sto3s = [1 0; -1/2 sqrt(3)/2; -1/2 -sqrt(3)/2];
    ConAmp_C3sto2r = (2/3) * [cos(i) cos(i-2/3*pi) cos(i+2/3*pi);-sin(i) -sin(i-2/3*pi) -sin(i+2/3*pi)];
    ConAmp_C2rto3s = [cos(i) -sin(i);cos(i-2/3*pi) -sin(i-2/3*pi);cos(i+2/3*pi) -sin(i+2/3*pi)];
    
    ConPower_C3sto2r = sqrt(2/3)*[cos(i) cos(i-2/3*pi) cos(i+2/3*pi);-sin(i) -sin(i-2/3*pi) -sin(i+2/3*pi)];
    ConPower_C2rto3s = sqrt(2/3)*[cos(i) -sin(i);cos(i-2/3*pi) -sin(i-2/3*pi);cos(i+2/3*pi) -sin(i+2/3*pi)];
    
    ConPower_C2sto2r = sqrt(2) * [sin(i+pi/3) sin(i); cos(i+pi/3) cos(i)];
    if(ConAmp == 0)
        ialpha(j) = ConPower_C3sto2s(1,:) * [ia(j);ib(j);ic(j)];
        ibeta(j) = ConPower_C3sto2s(2,:) * [ia(j);ib(j);ic(j)];

        id(j) = ConPower_C3sto2r(1,:) * [ia(j);ib(j);ic(j)];
        iq(j) = ConPower_C3sto2r(2,:) * [ia(j);ib(j);ic(j)];

        id_2(j) = ConPower_C2sto2r(1,:) * [ia(j);ib(j)];
        iq_2(j) = ConPower_C2sto2r(2,:) * [ia(j);ib(j)];
    else
        ialpha(j) = ConAmp_C3sto2s(1,:) * [ia(j);ib(j);ic(j)];
        ibeta(j) = ConAmp_C3sto2s(2,:) * [ia(j);ib(j);ic(j)];

        id(j) = ConAmp_C3sto2r(1,:) * [ia(j);ib(j);ic(j)];
        iq(j) = ConAmp_C3sto2r(2,:) * [ia(j);ib(j);ic(j)];
    end
    %A=[1 -0.5 -0.5;-0.5 1 -0.5;-0.5 -0.5 1];%磁链方程
    %C32*A*C23
    
    %B=[cos(i);cos(i-2/3*pi);cos(i+2/3*pi)];%磁链方程
    %C32*B
    
    %C=[0 1 -1;-1 0 1;1 -1 0];%转矩方程
    %C32*C*C23
    t(j) = i;
end
subplot(3,1,1);
plot(t,ia,'b', t,ib,'r', t,ic,'g')
title('ia,ib,ic')
subplot(3,1,2);
plot(t,ialpha,'k', t,ibeta,'r')
title('ialpha,ibeta')
subplot(3,1,3);
plot(t,id,'b', t,iq,'r')
title('id,iq')