leetcode -- 84. Largest Rectangle in Histogram

题目描述

题目难度：Hard
Given n non-negative integers representing the histogram’s bar height where the width of each bar is 1, find the area of largest rectangle in the histogram.

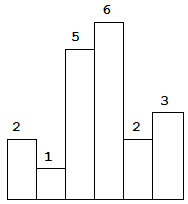
Above is a histogram where width of each bar is 1, given height = [2,1,5,6,2,3].

• Example:

Input: [2,1,5,6,2,3]
Output: 10

AC代码

参考自:https://leetcode.com/problems/largest-rectangle-in-histogram/discuss/225556/Java-solution-with-explanations-in-Chinese

• S1:双重遍历法
  本题要求的是一段连续的矩形，能够组成的面积最大的矩形的面积，所以，只要能够求出这一段矩形的位置的就可以了。最简单的想法，将所有的可能的组合都求解一遍，比较之后保留最大的那一个就好了，如下：

public static int largestRectangleArea(int[] heights) {
   int max = 0;
   for (int i = 0; i < heights.length; i++) {
       int min = heights[i];
       for (int j = i; j >= 0; j--) {
           if (heights[j] < min) {
               min = heights[j];
           }
           max = Math.max(max, min * (i-j+1));
       }
   }
   return max;
}
通过一个双重遍历，外层

遍历矩形的结束地址，内层遍历矩形起始地址，通过求算每一个组合的最大组成面积求解。时间复杂度为O(n^2)。

• S2:分治法
  上面的方法我们是依据矩形的起始、结束位置进行分类、求算，那么我们还可以使用另一种方法求算：按照组合矩阵的高度从低到高求解，然后取最大。我们知道，在给定的一组矩阵中，如果取高度为最低的那一个，那么宽度必然可取数组的长度。如，给定的一个数组[2,1,2]，那么当我们取高度为 1 ，那么宽度必然可取 3 。此时组合矩阵的面积是 3 。这时，组合矩阵取得是最低高度 1 。那么接下来，如果取一个更高的高度，那么这个高度为 1 的小矩阵必然不会包含在内，所以下一步要组成的矩阵必然在这个 1 的左边或者右边，这样一来，我们就可以看作，这个高度为 1 的小矩阵将整个矩阵序列分割成了两部分，我们下一步要判断的组合矩阵就在左部或者右部，如此一下，我们只需要求左右两部中能够组成的最大面积就好了，于是，一个数组[2,1,2]被最小值1分割成了两个数组[2]和[2]，如此一来，求[2,1,2]的解的问题变成了求[2]的解，而[2]的解只有一个 2 ，以此类推，我们就可以将任意一个大的问题分解成若干个小的问题，然后在这几个小问题中求最大值即可。代码如下：

public static int largestRectangleArea2(int[] heights) {
    return largest(heights, 0, heights.length-1);
}
public static int largest(int[] heights, int start, int end) {
    if (start > end) return 0;
    if (start == end) return heights[start];
    boolean sorted = true;
    int min = start;
    for (int i = start+1; i <= end; i++) {
        if (heights[i] < heights[i-1]) sorted = false;
        if (heights[i] < heights[min]) min = i;
    }
    if (sorted) {
        int max = heights[start] * (end - start + 1);
        for (int i = start+1; i <= end; i++) {
            max = Math.max(max, heights[i] * (end - i + 1));
        }
        return max;
    }
    return Math.max(Math.max(largest(heights, start, min-1), largest(heights, min+1, end)),
            heights[min] * (end - start + 1));
}

对于一个数组而言，可能成为最大值的解有三个：
最小值左部的某个解
最小值右部的某个解
包含当前最小值的解
另外，上面的方法中，通过判断当前的子数组是否是一个有序数组，来简化这个数组的判断，上面仅判断了由小到大的顺序，还可以通过判断是否是一个由大到小的顺序进一步提高判断效率。此算法的时间复杂度为O(n*log n)。

• S3:利用栈
  第一种方法的外层遍历，是组合矩阵的结束位置，然后在内层逐个遍历组合矩阵的开始位置。通过对这样一个模型的分析，对于以位置 i 结束的组合矩阵来说，它与当前位置之前的矩阵的高度有一定关系：
  如果 i 位置的高度大于 i-1 位置的高度，则在与这个位置之前的矩阵的组合中，不能以当前位置的高度作为组合矩阵的高度。如数组[1,2]，那么对于位置 2 来说，这两个位置的组合不能以 2 作为组合矩阵高度。
  如果 i 位置的高度不大于 i-1 位置的高度，则存在高度为当前高度的组合矩阵。如数组[2，1]，对于位置 1 ，有一种组合方法[1,1]，所以在这种情况下应该判断一下。

另外，我们知道，对于一个高度递增的数组来说，很容易求出其组合矩阵的最大面积，那么是否可以将任意一个矩阵转化为一个高度递增的矩阵序列？如将一个数组[2,3,1,3,5]变成[1,1,1,3,5]，但是这个过程中对 2 作了改变，我们要通过一定办法弥补这里的改变，一种方法是，在作改变前，将其能够组成的组合矩阵的最大面积记录下来，完了之后便可以对其做出改变了。对于上面那个例子，实际上我们是对两个递增的数组求解：[2,3]和[1,1,1,3,5]，而它们之间的最大解必然与[2,3,1,3,5]的解相同。于是，将一个不规则数组转化为若干有序数组，再进行求解，便是本方法的思想。下面是利用栈的一种实现，利用栈的话不需要对原数据进行修改，而是直接将原数组截取成多个有序数组，通过保存索引值确定当前的组合矩阵的宽度：

public static int largestRectangleArea3(int[] heights) {
    Stack<Integer> stack = new Stack<>();
    int n = heights.length;
    int max = 0;
    for (int i = 0; i <= n; i++) {
        while (!stack.empty() && (i >= n || heights[stack.peek()] > heights[i])) {
            int top = stack.pop();
            int h = heights[top];
            int w = stack.empty() ? i : (i-stack.peek()-1);
            max = Math.max(max, h*w);
        }
        stack.push(i);
    }
    return max;
}

• S4:最长宽度法
  我们知道，由多个矩阵组成的组合矩阵，其宽度为矩阵的数量，高度为矩阵中高度最低的那一个。所以，对于任意一个位置的矩阵，假设此时的组合矩阵高度为当前位置矩阵的高度，我们只需要求出这时的组合矩阵的最大宽度，便可以求出以当前矩阵的高度为高度的组合矩阵的最大面积，那么我们只需要求出每一个位置能够形成的最大解，便能够得到本题的解。要求出某个位置的最大解，如 i ，可以这样理解，从数组[0,…,n]中找到最大的一段[start,…,i,…end]，并且在这段中，位置 i 处的高度最低，那么此时这段矩阵组成的组合矩阵的面积必然是(end-start) * heights[i]。所以我们要在位置 i 的左边找到一段[start,…,i]，是的这里面每一个矩阵的高度都大于等于 i 处的高度，同理，还要在 i 的右边找到一段[i,…end]，找到这些之后，位置 i 处的解就可以求得了。所以，对于每一个位置，只要找到在 i 的左边第一个小于 i 处高度的位置 start ，再找到 i 的右边第一个小于 i 处高度的位置 end 便可。而这个数据可以通过两个遍历求解。

public static int largestRectangleArea4(int[] heights) {
    int n = heights.length;
    if (n == 0) return 0;
    int[] leftLess = new int[n], rightLess = new int[n];
    // find left
    leftLess[0] = 0;
    for (int i = 1; i < n; i++) {
        int p = i-1;
        while (true) {
            if (p >= 0 && heights[i] <= heights[p]) {
                p -= leftLess[p] + 1;
            } else {
                leftLess[i] = i - p - 1;
                break;
            }
        }
    }
    // find right
    rightLess[n-1] = 0;
    for (int i = n-2; i >= 0; i--) {
        int p = i+1;
        while (true) {
            if (p < n && heights[i] <= heights[p]) {
                p += rightLess[p] + 1;
            } else {
                rightLess[i] = p - 1 - i;
                break;
            }
        }
    }
    int max = 0;
    for (int i = 0; i < n; i++) {
        max = Math.max(max, heights[i] * (leftLess[i] + rightLess[i] + 1));
    }
    return max;
}

使用一个数组 leftLess 保存每个位置的左边高度大于当前位置高度的矩阵数量，rightLess 同理。具体的求解方法为：对于位置 i ，如果 i-1 处的高度大于 i 处的高度，那么因为leftLess[i-1]保存的是大于位置 i-1 处高度的数量，那么这些位置的高度必然也大于位置 i 处的高度，所以，我们可以直接跳过1 + leftLess[i-1]个位置，判断下一个位置 p 处的高度是否大于 i 处的高度，如果还是大于，那么还要继续跳过leftLess[p] + 1个位置，再判断…直到 p 处的高度小于 i 处的高度，此时在 i 的左边比 i 处高度大的矩阵的数量就是i - p - 1个。对于 rightLess 的求解同理。