Leetcode-84. Largest Rectangle in Histogram [C++][Java]

Leetcode-84. Largest Rectangle in Histogramhttps://leetcode.com/problems/largest-rectangle-in-histogram/description/

一、题目描述

Given an array of integers heights representing the histogram's bar height where the width of each bar is 1, return the area of the largest rectangle in the histogram.

Example 1:

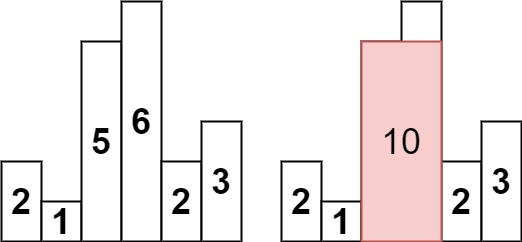
Input: heights = [2,1,5,6,2,3]
Output: 10
Explanation: The above is a histogram where width of each bar is 1.
The largest rectangle is shown in the red area, which has an area = 10 units.

Example 2:

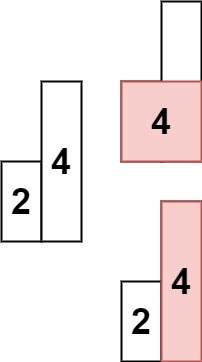
Input: heights = [2,4]
Output: 4

Constraints:

• 1 <= heights.length <= 10^5
• 0 <= heights[i] <= 10^4

二、解题思路

单调栈+动态规划

• 时间复杂度为 O(mn)

• 空间复杂度为 O(n)

【C++】

class Solution {
public:
    int largestRectangleArea(vector<int>& heights) {
        int n = heights.size();
        if (n == 0) {
            return 0;
        }
        int res = 0;
        vector<int> left(n, -1), right(n, n);
        stack<int> st;
        for (int j = 0; j < n; ++j) {
            while (!st.empty() && heights[st.top()] >= heights[j]) {
                right[st.top()] = j;
                st.pop();
            }
            if (!st.empty()) {
                left[j] = st.top();
            }
            st.push(j);
        }
        for (int j = 0; j < n; ++j) {
            res = max(res, heights[j] * (right[j] - left[j] - 1));
        }
        return res;
    }
};

【Java】

class Solution {
    public int largestRectangleArea(int[] heights) {
        if (heights == null || heights.length == 0) {
            return 0;
        }
        int n = heights.length, res = 0;
        int[] left = new int[n];
        int[] right = new int[n];
        Arrays.fill(left, -1);
        Arrays.fill(right, n);
        Stack<Integer> st = new Stack<>();
        for (int j = 0; j < n; j++) {
            while (!st.isEmpty() && heights[st.peek()] >= heights[j]) {
                right[st.pop()] = j;
            }
            if (!st.isEmpty()) {
                left[j] = st.peek();
            }
            st.push(j);
        }
        for (int j = 0; j < n; j++) {
            res = Math.max(res, heights[j] * (right[j] - left[j] - 1));
        }
        return res;
    }
}