Codeforces Contest 1093 problem E Intersection of Permutations——CDQ分治

最新推荐文章于 2022-07-06 11:01:53 发布

天翼之城*

最新推荐文章于 2022-07-06 11:01:53 发布

阅读量381

点赞数

CC 4.0 BY-SA版权

分类专栏：分治

本文链接：https://blog.youkuaiyun.com/tianyizhicheng/article/details/86586646

分治专栏收录该内容

8 篇文章

订阅专栏

本文介绍了一种解决二维平面区间查询与更新问题的方法，通过使用离线查询和树状数组进行点的删除与添加，实现对两个数组的交集元素数量的高效计算。文章详细解释了算法流程，并提供了完整的C++代码实现。

You are given two permutations a and b, both consisting of n elements. Permutation of n elements is such a integer sequence that each value from 1 to n appears exactly once in it.

You are asked to perform two types of queries with them:

1 la ra lb rb — calculate the number of values which appear in both segment [la;ra] of positions in permutation a and segment [lb;rb] of positions in permutation b;
2 x y — swap values on positions x and y in permutation b.
Print the answer for each query of the first type.

It is guaranteed that there will be at least one query of the first type in the input.

Input
The first line contains two integers n and m (2≤n≤2⋅105, 1≤m≤2⋅105) — the number of elements in both permutations and the number of queries.

The second line contains n integers a1,a2,…,an (1≤ai≤n) — permutation a. It is guaranteed that each value from 1 to n appears in a exactly once.

The third line contains n integers b1,b2,…,bn (1≤bi≤n) — permutation b. It is guaranteed that each value from 1 to n appears in b exactly once.

Each of the next m lines contains the description of a certain query. These are either:

1 la ra lb rb (1≤la≤ra≤n, 1≤lb≤rb≤n);
2 x y (1≤x,y≤n, x≠y).
Output
Print the answers for the queries of the first type, each answer in the new line — the number of values which appear in both segment [la;ra] of positions in permutation a and segment [lb;rb] of positions in permutation b.

Example
inputCopy
6 7
5 1 4 2 3 6
2 5 3 1 4 6
1 1 2 4 5
2 2 4
1 1 2 4 5
1 2 3 3 5
1 1 6 1 2
2 4 1
1 4 4 1 3
outputCopy
1
1
1
2
0
Note
Consider the first query of the first example. Values on positions [1;2] of a are [5,1] and values on positions [4;5] of b are [1,4]. Only value 1 appears in both segments.

After the first swap (the second query) permutation b becomes [2,1,3,5,4,6].

After the second swap (the sixth query) permutation b becomes [5,1,3,2,4,6].

题意：

给你两个长度为n的数组，每个数组的元素都是1到n之间且唯一的，给你m个操作
1 x y表示交换第二个数组中位置x,y的数
2 a b c d表示询问你第一个数组从a到b，第二个数组从c到d中有哪些元素是相同的

题解：

我们可以把数字i在第一个数组中的位置当做x，第二个数组中的位置当做y，那么这道题就是一个二维平面求一块区间点的数量：
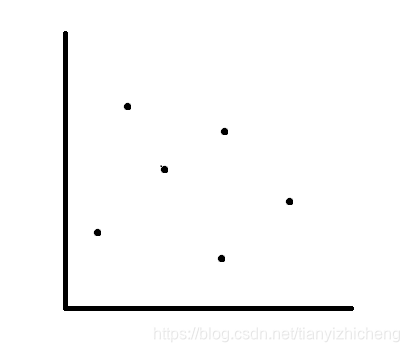
在这里插入图片描述
交换点的时候我们先要把原来的点就是x的坐标：ch1[p2[x]],ch2[p2[x]]，y的坐标:ch1[p2[y]],ch2[p2[y]]删掉，然后在加进去新的坐标。

#include<iostream>
#include<stdio.h>
#include<stdlib.h>
#include<cstring>
#include<map>
#include<queue>
#include<vector>
using namespace std;
const int N=4e5+5;
struct node
{
	int op,x,y,k,pos,Id;
	node(){}
	node(int op,int x,int y,int k,int pos,int Id):op(op),x(x),y(y),k(k),pos(pos),Id(Id){}
}a[N*4],tmp[N*4];
int num[N];
int lowbit(int x)
{
	return x&(-x);
}
void add(int x,int v)
{
	for(int i=x;i<N;i+=lowbit(i))
		num[i]+=v;
}
int query(int x)
{
	int ans=0;
	for(int i=x;i;i-=lowbit(i))
		ans+=num[i];
	return ans;
}
void clear(int x)
{
	for(int i=x;i<N;i+=lowbit(i))
		num[i]=0;
}
int p1[N],p2[N],ch1[N],ch2[N],ans[N];
void CDQ(int l,int r)
{
	if(l==r)
		return ;
	int mid=l+r>>1;
	CDQ(l,mid),CDQ(mid+1,r);
	int p1=l,p2=mid+1,p=0;
	while(p1<=mid&&p2<=r)
	{
		if(a[p1].x<=a[p2].x)
		{
			tmp[++p]=a[p1];
			if(a[p1].op==1)
				add(a[p1].y,a[p1].k);
				p1++;
		}
		else
		{
			tmp[++p]=a[p2];
			if(a[p2].op==2)
				ans[a[p2].Id]+=a[p2].k*query(a[p2].y);
				p2++;
		}
	}
	while(p1<=mid)
		tmp[++p]=a[p1],p1++;
	while(p2<=r)
		ans[a[p2].Id]+=a[p2].k*query(a[p2].y),tmp[++p]=a[p2],p2++;
	for(int i=1;i<=p;i++)
	{
		if(tmp[i].op==1&&tmp[i].pos<=mid)
			clear(tmp[i].y);
		a[l+i-1]=tmp[i];
	}
}
int main()
{
	int n,m,cnt=0,num=0;
	scanf("%d%d",&n,&m);
	for(int i=1;i<=n;i++)
		scanf("%d",&p1[i]),ch1[p1[i]]=i;
	for(int i=1;i<=n;i++)
		scanf("%d",&p2[i]),ch2[p2[i]]=i;
	for(int i=1;i<=n;i++)
		a[++cnt]=node(1,ch1[i],ch2[i],1,cnt,0);
	while(m--)
	{
		int op,x1,x2,y1,y2;
		scanf("%d",&op);
		if(op==2)
		{
			scanf("%d%d",&x1,&y1);
			a[++cnt]=node(1,ch1[p2[x1]],ch2[p2[x1]],-1,cnt,0);//p2[x1],p2[y1]两个值的位置删掉
			a[++cnt]=node(1,ch1[p2[y1]],ch2[p2[y1]],-1,cnt,0);
			swap(p2[x1],p2[y1]);
			ch2[p2[x1]]=x1,ch2[p2[y1]]=y1;
			a[++cnt]=node(1,ch1[p2[x1]],ch2[p2[x1]],1,cnt,0);
			a[++cnt]=node(1,ch1[p2[y1]],ch2[p2[y1]],1,cnt,0);

		}
		else
		{
			scanf("%d%d%d%d",&x1,&x2,&y1,&y2);
			x1--,y1--;
			a[++cnt]=node(2,x1,y1,1,cnt,++num);
			a[++cnt]=node(2,x2,y2,1,cnt,num);
			a[++cnt]=node(2,x1,y2,-1,cnt,num);
			a[++cnt]=node(2,x2,y1,-1,cnt,num);
		}
	}
	CDQ(1,cnt);
	for(int i=1;i<=num;i++)
		printf("%d\n",ans[i]);
		return 0;
}