下垂控制中低通滤波器设计

下垂控制中功率计算低通滤波器截止频率的分析与设计

摘要

下垂控制方法已广泛应用于微电网中，以实现分布式发电之间的均等功率分配。在实际应用中，通常需要低通滤波器来抑制计算得到的瞬时功率中的谐波和噪声，从而获得用于生成频率和电压参考值的平均功率。然而，现有研究尚未对低通滤波器进行系统化设计。本文通过提出下垂控制系统的小信号模型，分析了低通滤波器对系统稳定性的影响，并提供了一种最优截止频率的设计方法。仿真结果验证了所提出设计方法的有效性。

关键词

下垂控制，低通滤波器，截止频率，小信号分析

一、引言

随着微电网等独立电力系统中电力需求的增长，单逆变器接口分布式发电（DG）在许多情况下难以满足系统容量和可靠性提升的需求，因此并联逆变器成为一种有效的解决方案，并已在实践中广泛应用。考虑到微电网中分布式发电机的分布式地理位置，下垂控制方法无需通信即可实现分布式发电机之间的均等功率分配，因此被广泛用于微电网中并联逆变器的协调控制[1,2]。

然而，下垂控制存在一些缺点，例如频率和电压幅值的偏差、无功功率分配性能较差以及有功和无功功率控制之间的耦合，这些都会降低下垂控制的性能。此外，由于分布式发电机不能被视为理想的交流电源，系统中存在谐波和噪声，影响了控制精度。因此，在功率分配环路中引入了用于功率计算的低通滤波器（LPFs），以平滑生成的频率和电压参考值。然而，现有研究尚未对低通滤波器进行系统化设计，截止频率大多凭经验选取。

针对上述问题，本文研究了低通滤波器截止频率对系统性能的影响，旨在为下垂控制中的功率计算设计一种最优的低通滤波器设计方法。基于小信号模型，分析中考虑了系统稳定性、动态响应和功率分配精度。基于双并联逆变器系统的仿真结果验证了所提出设计方法的有效性。

II. 背景

通常情况下，微电网中的并联逆变器采用下垂控制作为电压源，电压幅值和频率的参考值可通过(1)计算得出。

$$
\begin{aligned}
& \omega = \omega_0 - m(P - P_0)s^{-1} \
& E = E_0 - n(Q - Q_0)s^{-1}
\end{aligned}
\tag{1}
$$

其中，$\omega$和$E$是由功率分配环路产生的参考值，$P$和$Q$分别为计算出的有功功率和无功功率，而$P_0$和$Q_0$分别为额定有功功率和额定无功功率。$m$和$n$（定义为正值）为下垂系数。$\omega_f$是低通滤波器的截止频率。

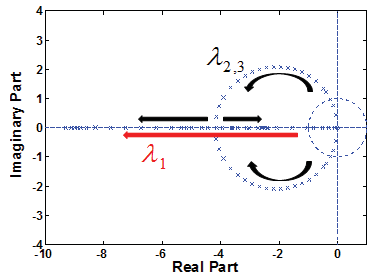
该外环控制被定义为分布式发电的功率分配环路。然后讨论首先从一个未包含用于计算有功和无功功率的低通滤波器的并联模型开始。基于这个不完整的模型，通过FFT算法分析了阶跃输入下无功功率的频谱分布，结果如图1所示（以$Q_1$为例）。

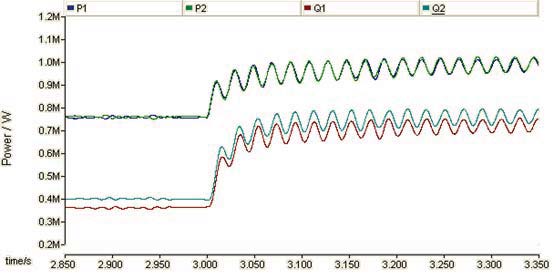
图1中的微小尖峰分别出现在PWM控制器的开关频率和并联系统的基波频率附近。前者已经被与逆变器级联的物理LC滤波器大部分抑制，对波形的影响微小，而后者在整个系统的动态响应和稳态精度中起着更为重要的作用。

在实际中，负载扰动和电压扰动难以消除，因此根据公式（1），基于测量电压和电流得到的计算功率将无法保持恒定，并会直接影响电压幅值和频率的参考值；而参考值的变化又会反馈并反过来加剧功率的畸变。在动态过程中，由于电压环的响应速度相较于电流环较慢，后续的U-I相位差也会影响计算功率的平滑性。因此，在基波频率（50赫兹）附近的谐波和噪声将出现在功率和电压波形中，甚至在暂态过程中变得更加严重。

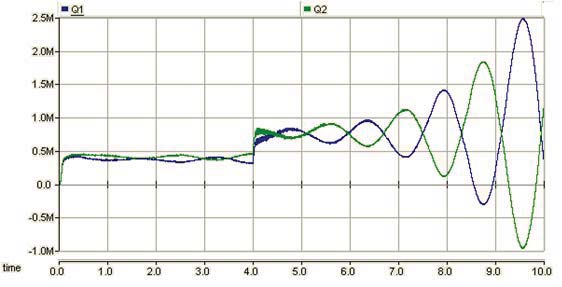
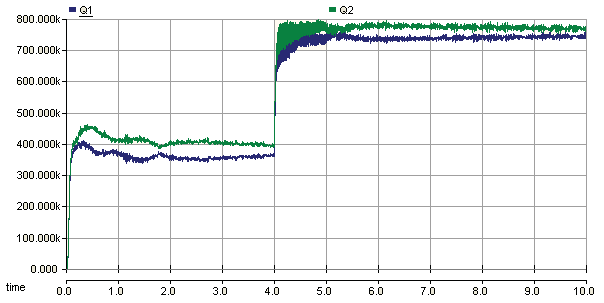
负载增加时的仿真结果如图2和图3所示。图2显示了逆变器#i（i=1, 2）的有功功率$P_i$和无功功率$Q_i$的波形。由于功率畸变引起的电压幅值参考值$E_{con}$和频率参考值$f_{con}$的波动分别如图3a和图3b所示（以逆变器#1为例）。

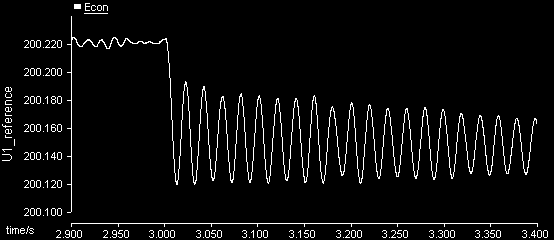
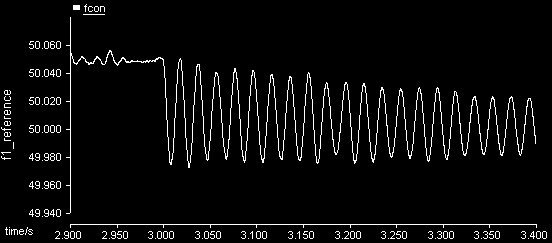
由于上述谐波的存在，具有特定截止频率的低通滤波器作为下垂控制系统中不可或缺的组成部分，被用于提取高质量的平均有功和无功功率，并减少谐波和噪声[3]。

根据分析，基波频率（50赫兹）附近的谐波和噪声会显著增加功率畸变并降低逆变器输出电压质量，且根据其幅值大小，甚至可能导致微电网系统失稳[4]。同时，它们也与系统动态响应密切相关。当在不同负载条件之间切换时，如果低通滤波器的带宽设计过小，功率控制环的响应时间将会更长。因此，在这种内在矛盾下，保持快速响应与电源质量之间的平衡至关重要，这对滤波器的设计提出了挑战。

许多解决方案已被提出以解决此问题。然而，与单相系统或不平衡三相系统中的二倍频分量不同，这类谐波具有一定的随机性，难以通过[5]中提到的延时求和模块消除。

一些研究人员甚至采用高阶低通滤波器以在通带内实现更平坦的顶部和更陡峭的下降沿。相关实验结果表明，高阶贝塞尔、巴特沃斯和切比雪夫滤波器均能在抑制谐波和改善滤波器性能方面起到有效作用[5, 6]。

然而，在嵌入式系统中应用下垂控制算法时，计算应占用较少内存且具有较低的计算成本，同时不牺牲速度、暂态响应和谐波衰减[6]，这一点至关重要。因此，在通常情况下，若一阶低通滤波器能够满足电压精度和电能质量的要求，则仍应优先选用（后续仿真已验证）。因此，下文主要讨论一阶低通滤波器。

III. 基于小信号分析的低通滤波器设计

本节通过在平衡点附近进行小信号分析，以评估低通滤波器截止频率对下垂控制系统的影响。

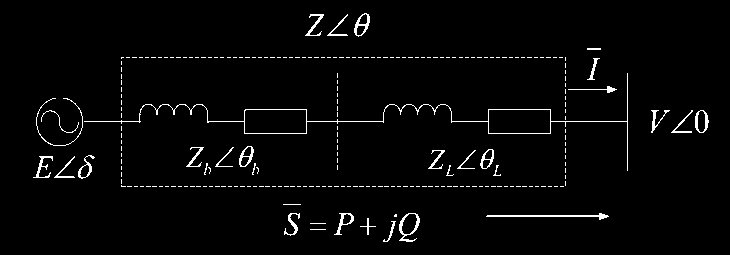
基于图4所示的单个分布式发电系统等效电路，当$V$和$E$以线电压测量时，从分布式发电到微电网公共连接点的传输功率可表示为(2)。

$$
\begin{aligned}
P &= \frac{EV}{Z} \cos(\delta - \theta) - \frac{V^2}{Z} \cos \theta \
Q &= \frac{EV}{Z} \sin(\delta - \theta) - \frac{V^2}{Z} \sin \theta
\end{aligned}
\tag{2}
$$

其中$Z \angle \theta = Z_b \angle \theta_b + Z_L \angle \theta_L$，表示总阻抗是逆变器输出阻抗和线路阻抗的组合。当将$Z$表示为$R + jX$时，(2)可推导为(3)。

$$
\begin{aligned}
P &= \frac{1}{R^2 + X^2} \left[ (EV \cos \delta - V^2)R + (EV \sin \delta)X \right] \
Q &= \frac{1}{R^2 + X^2} \left[ (EV \sin \delta - V^2)X - (EV \cos \delta)R \right]
\end{aligned}
\tag{3}
$$

为了简化分析，我们假设内电压控制器的带宽远高于功率分配环路，因此可以认为其能够足够快地跟踪参考值，并忽略暂态偏差。此外，$\delta$的值非常小，公共连接点电压$V$基本保持恒定。对(1)和(3)进行线性化后，得到

$$
\begin{aligned}
\Delta \omega &= -m \Delta P \
\Delta E &= -n \Delta Q \
\Delta P &= k_{pe} \Delta E + k_{pd} \Delta \delta \
\Delta Q &= k_{qe} \Delta E + k_{qd} \Delta \delta
\end{aligned}
\tag{4}
$$

其中$\Delta$表示相应变量相对于稳态点的小幅偏差，且

$$
\begin{aligned}
k_{pe} &= \frac{\partial P}{\partial E} = \frac{RV \cos \delta + X V \sin \delta}{R^2 + X^2} \approx \frac{RV}{R^2 + X^2} \
k_{pd} &= \frac{\partial P}{\partial \delta} = \frac{-RV \sin \delta + X V \cos \delta}{R^2 + X^2} \approx \frac{X V}{R^2 + X^2} \
k_{qe} &= \frac{\partial Q}{\partial E} = \frac{X V \cos \delta - R V \sin \delta}{R^2 + X^2} \approx \frac{X V}{R^2 + X^2} \
k_{qd} &= \frac{\partial Q}{\partial \delta} = \frac{-X V \sin \delta - R V \cos \delta}{R^2 + X^2} \approx \frac{-R V}{R^2 + X^2}
\end{aligned}
\tag{5}
$$

考虑到低通滤波器的存在，可推导出小信号方程(4)

$$
\begin{aligned}
\Delta \omega(s) &= -m \left( k_{pe} \Delta E(s) + \frac{k_{pd}}{s + \omega_f} \Delta \delta(s) \right) \
\Delta E(s) &= -n \left( k_{qe} \Delta E(s) + \frac{k_{qd}}{s + \omega_f} \Delta \delta(s) \right)
\end{aligned}
\tag{6}
$$

基于上述假设和关系$\Delta \delta(s) = \omega \Delta \delta(s)/s$，将其代入(6)式，可得

$$
s^3 \Delta \delta(s) + a_2 s^2 \Delta \delta(s) + a_1 s \Delta \delta(s) + a_0 \Delta \delta(s) = 0
\tag{7}
$$

其中

$$
\begin{aligned}
a_2 &= \omega_f + 2\omega_{qe} > 0 \
a_1 &= \omega_f (\omega_{qe} + \omega_{pd}) + \omega_f^2 > 0 \
a_0 &= \omega_f \cdot n V E k_{pd} m > 0
\end{aligned}
\tag{8}
$$

可以等效地写为小信号响应的特征方程：

$$
a_3 \lambda^3 + a_2 \lambda^2 + a_1 \lambda + a_0 = 0
\tag{9}
$$

根据劳斯判据，动态响应和闭环稳定性可以通过特征方程的系数来确定。表I是式(9)的劳斯表。

$s^3$	1	$(\omega_{qe} + \omega_{pd})\omega_f + \omega_f^2$
$s^2$	$\omega_f + 2\omega_{qe}$	$n V E k_{pd} m \omega_f$
$s^1$	$a_1 = a_2 a_0 / a_1 - a_0$	0
$s^0$	$n V E k_{pd} m \omega_f$

表 I 特征方程的劳斯判据

劳斯判据指出，具有正实部的根的个数等于第二列中符号变化的次数，因此$a_1 = a_2 a_0 / a_1 - a_0$应为正数以确保系统稳定。于是我们得到

$$
\omega_f > \frac{m V E (n V R)}{(n V X)^2 + (n V X)(2 Z)}
\tag{10}
$$

这是截止频率设计的基本前提。

考虑到过大的$\omega_f$难以滤除谐波和噪声，并影响系统稳态精度，我们需要使指定频率附近的谐波衰减超过90%，因此截止频率$\omega_f$必须设计得至少比基波频率[6]低一个数量级。

IV. 仿真验证

PSCAD仿真被用于验证该设计。为了研究动态功率分配，两个分布式发电机的线路阻抗略有不同，作为不平衡因子引入系统。关键参数的值见表II。

表 II 仿真用DGS参数

参数	值	参数	值
$m$	0.0001	$n$	0.0001
$E_{con}$	200 伏特	$f_{con}$	50 赫兹
$P_{con}$	2000 瓦特	$Q_{con}$	3000 乏
$R_{line#1}$	0.1 欧姆	$R_{line#2}$	0.15 欧姆

第一次仿真旨在研究不同截止频率对电压幅值参考值的影响。波形如图6所示：在$t = 2$秒时，负载从1500瓦特 + 750乏增加到2000瓦特 + 1500乏，因此参考值从200.22伏下降到200.15伏。比较表明，较小的$\omega_f$在动态响应方面表现较差，而较大的$\omega_f$在提取平均功率以及滤除谐波和噪声方面存在困难。

(a)
(b)
(c)
(d)

为测量动态响应和稳态精度，进行了一系列仿真，结果以$\Delta Q$和$T_s$的形式显示在表III中。需要注意的是，$\Delta Q$定义为无功功率的偏差，而$T_s$定义为频率参考值的调节时间。

表 III 不同LPF截止频率下的测量系统参数

$\omega_f$ (rad/s)	1	5	10	15	20	25	30	50	100	200	300
$\Delta Q$ / 乏	不稳定	100	50	25	20	25	28	30	35	30	30
$T_s$ / s	不稳定	>1	0.8	0.65	0.55	0.54	0.54	0.52	0.5	0.5	0.5

如图7所示，在相同的负载变化条件下，第二次仿真用于验证稳定性和电能质量。从图7a可以看出，即使根据图5，截止频率为1弧度/秒的低通滤波器是可接受的，但由于稳定裕度较小，系统仍容易失控。图7b和图7d表明，无论导致功率畸变的原因如何，$\omega_f$过小或过大都会造成电能质量下降。

从表III可以看出，调节时间随着$\omega_f$的增加而减小，但当$\omega_f > 20\,\text{rad/s}$时，调节时间几乎保持不变。至于功率偏差，$\omega_f$与$\Delta Q$之间没有简单的对应关系，但在$\omega_f = 20\,\text{rad/s}$时$\Delta Q$最小。因此，截止频率为20弧度/秒的低通滤波器是最佳选择。

V. 结论

本文研究了功率计算低通滤波器在下垂控制并联逆变器系统中的影响。基于小信号分析提出了一种低通滤波器截止频率设计方法。按照所提出的设计方法，设计的低通滤波器能够在动态性能、稳态精度和系统稳定性之间取得良好折衷。通过对双并联逆变器系统的仿真结果验证了所提出设计方法的有效性。