基于内部滚动质量的AUV横滚控制

基于内部滚动质量的自主水下航行器横滚控制

摘要

一个稳定的自主水下航行器（AUV）对于水下测量活动至关重要。以往的研究表明，海底地形测量和侧扫成像效果不佳与航行器不必要的横滚运动有关。随着自主水下航行器体积的减小，这一问题日益突出。这会导致自主水下航行器稳心高度降低，从而影响其横滚轴固有自稳定能力。本文展示了利用内部滚动质量机构（IRM机构）主动稳定自主水下航行器横滚运动的方法。我们通过旋转具有偏心重心的整个电子托盘，产生所需的力矩以稳定横滚运动。文中详细讨论了该机构的机械设计及其动力学建模过程。基于辨识值建立的线性模型，设计了一个比例‐积分(PI)控制器。水池试验和野外试验的结果验证了该机构在调节自主水下航行器横滚运动方面的有效性。

1 引言

稳定的自主水下航行器（AUV）对于水下探测至关重要，例如利用侧扫声呐进行海底成像、利用多波束声呐进行测深测绘以及利用水下相机进行图像拼接。与偏航和俯仰相比，鱼雷形AUV的横滚具有较小的惯性矩和阻力。因此，当AUV受到螺旋桨扭矩、未知干扰以及转弯时的倾斜运动影响时，其滚转动力学会呈现振荡特性。若无滚转稳定措施，AUV不必要的滚转运动可能会带来问题 [7]。

辛格，等[9],在其测深论文中指出，横摇偏差是最主要的误差源，因为它直接影响所勘测区域的坡度。柯克伍德，等[3]指出，横摇稳定性对多波束测绘至关重要，具有高优先级。在侧扫声呐应用中，自主水下航行器横摇运动可能导致叠掩现象发生[10]；受影响的数据样本难以解释，需要被舍弃。不必要的滚转运动还可能影响自主水下航行器的潜航和转向性能。这是因为大多数反馈控制器的设计都基于偏航与俯仰运动解耦的假设。当自主水下航行器的横滚非零时，该假设被破坏，从而可能影响解耦控制器的性能[6]。

随着自主水下航行器日益小型化，这一问题正变得愈发突出。为了降低制造成本并便于单人或双人部署，小型自主水下航行器被设计得更小。然而，小型自主水下航行器对内部组件的布置造成了限制，并导致其稳心高度降低，从而影响了横滚轴方向上的固有自稳定能力。因此，小型自主水下航行器容易产生振荡性横摇运动。

在本研究中，我们探讨利用内部滚动质量机构来主动稳定自主水下航行器的滚转运动。内部执行器具有若干显著优势：首先，它们可在低速条件下使用，而此时鳍片已失去作用；其次，它们可完全置于航行器内部，因而不易因碰撞或腐蚀而损坏 [11]；第三，它们不会产生外部阻力。

在水下航行器应用中使用内部移动质量并非新概念。该技术已被应用于斯洛克姆、喷雾滑翔机和海滑翔机等水下滑翔机 [5]。一些自主水下航行器也采用了内部移动质量技术，例如混合型自主水下航行器——eFolaga [1]，其通过沿纵轴移动电池实现俯仰控制。然而，由于可用的横向空间有限，难以实现有效的线性运动，因此利用内部质量进行滚转控制的情况较为罕见。此外，线性运动需要为移动质量设置滑行道，而在内部空间已被关键组件占据的情况下，这在实践中难以实现。我们通过设计一种滚动质量机构克服了这一限制，该机构将整个电子托盘（包括电池）作为移动质量加以利用。

移动质量能够相对于自主水下航行器（AUV）的纵轴旋转——因此我们称之为内部滚动质量机构（IRM机构）。内部滚动质量（IRM）的重心（CG）是非对称中心的。通过旋转IRM，我们可以有效改变AUV的重心（CG）。利用通过重心（CG）的重力，我们因此可以产生所需的力矩来稳定滚转动力学。

本文中，我们通过采用内部移动质量机构（IRM）实现主动滚转稳定，以解决不必要的横滚运动问题。据我们所知，我们是首个报道使用内部移动质量来稳定欠驱动、尾部推进且由鳍控制的自主水下航行器（AUV）滚转的团队。我们通过在STARFISH自主水下航行器（[4]）上的实施，展示了内部移动质量机构（IRM mechanism）的设计。STARFISH自主水下航行器是一种流线型具有单推进器和尾部四个控制面的自主水下航行器。这是商业和研究界中自主水下航行器最广泛使用的构型。因此，我们对内部移动质量机构的讨论与当前许多在用的自主水下航行器密切相关且具有广泛适用性。

本文的结构如下：在第2节中，我们介绍了内部移动质量机构的机械设计。接着在第3节中建立了自主水下航行器的滚转动力学模型，其中内部移动质量作为执行器。在第4节中，我们给出了系统辨识的结果，其中模型的参数被辨识出来。在第5节中，我们展示了如何设计控制器以调节滚转运动。实验结果在第6节中给出。最后，在第7节中我们给出了结论。

2 机械设计

2.1 STARFISH自主水下航行器

STARFISH自主水下航行器为鱼雷形状，直径为200毫米。它们被设计成模块化结构。基本型STARFISH自主水下航行器由3个基本段组成——头部段、指挥与控制段和尾部段。总长度约为1.6米，重量约为45公斤。可根据应用需求在基本型STARFISH自主水下航行器上增加额外的有效载荷段。我们目前拥有的有效载荷包括多普勒速度计程仪（DVL）段、侧扫声呐段和化学传感器段。感兴趣的读者可参考[4]以获取有关STARFISH自主水下航行器各段之间机械、电气和软件接口的详细讨论。

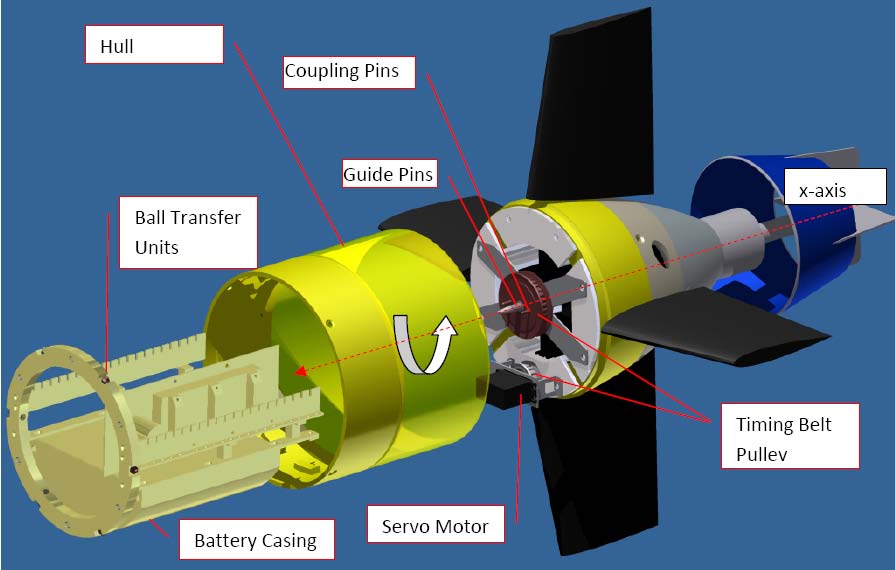
2.2 设计要求

我们需要一种能够在横移轴上移动自主水下航行器重心的机制，以便通过±5◦改变自主水下航行器的横滚平衡。为了移动重心，我们需要某种形式的移动质量，因此可以采用线性移动质量或旋转质量。我们使用旋转质量的实现方式如图1所示。

驱动由安装在尾部段底端支架上的伺服电机提供，其最大力矩为1.92 牛·米，最大速度为6.16 弧度/秒。通过两个同步带轮将动力从伺服电机传递到中心轴。驱动带轮传动比为1:2，从而使输出力矩增大两倍。导向销用于引导整个尾部托盘（图中为亮镍）装配入壳体。两个联轴销用于将力矩从中心带轮传递到尾部托盘。由于尾部托盘的主要质量来自放置在下半部分的电池，因此当尾部托盘在壳体内横滚时，我们有效地改变了重心。

此设计满足以下要求：

2.2.1 空间约束

受限于直径为 200 mm 的自主水下航行器，线性移动质量缺乏足够的滑行道以实现重心的有效变化。此外，电子设备和电池等现有组件已占据了尾部段的大部分空间。因此，在不影响自主水下航行器其他部分组件的前提下，我们将尾部段的所有现有组件整合到一个尾部托盘上，并将该尾部托盘作为我们的移动质量。我们在不改变现有尾部段壳体（例如延长）的情况下，成功为伺服电机、两个皮带轮和一个同步带找到了安装空间。

2.2.2 能耗

将机构置于尾部段，我们利用现有的微控制器来控制伺服电机。同一微控制器用于推进器和舵翼控制。在尾部托盘的外圈布置了六个球形转移装置，有效利用该环作为轴承，实现低摩擦的旋转运动。为了提供所需的力矩和精度，我们采用了一款Futaba数字伺服电机，其最大功耗为12瓦特。我们使用同步带传动系统，其动力传输损耗较低。

2.2.3 装配简便性

装配便捷性是重要的设计标准之一。我们偶尔需要拆卸车辆以进行常规维护和维修。采用该设计后，组装和拆卸工作均可由我们实验室的一名工程师在半小时内完成。

2.2.4 重心的有效变化

伺服电机的可用范围为 80◦。经过滑轮比后，范围减小到 40◦。通过将内部移动质量置于中心，我们能够将内部移动质量滚动至 ±20◦；这相当于重心的有效变化，从而在平衡状态下产生±5◦¹的横滚角。

3 建模

坐标参考系 (b) 受力分析图

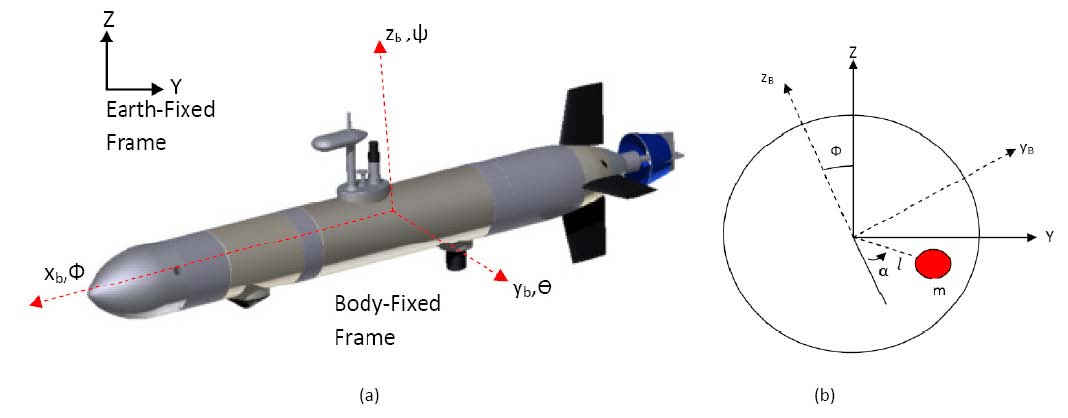
在本节中，我们推导考虑由于内部移动质量（IRM）引起的重心（CG）偏移时自主水下航行器（AUV）横滚的动力学模型。自主水下航行器的六自由度（DOF）动力学模型通常由一组关于两个坐标系的非线性方程描述，如图2(a)所示。有关该模型的详细讨论见[2, 8]。然而，就本文而言，我们将分析仅限于横滚运动，并将其他自由度引起的耦合扭矩视为扰动。

在图2(a)中，我们将固连体坐标系置于自主水下航行器（AUV）的浮心（CB）处。因此浮心相对于固连体坐标系位于zb= 0和yb= 0。为了提供扶正力矩，重心位于浮心下方。因此，重心位置（yg,zg）相对于固连体坐标系的zg为负值。

根据牛顿第二运动定律（旋转），我们可以将净总力矩写为惯性矩Ixx与横滚角加速度 φ的乘积。
$$
∑τ= Ixx φ¨. \tag{1}
$$

外部扭矩的总和由以下组成部分构成：

3.1 静水扶正力矩

静水扶正力矩是航行器重量W和浮力B共同作用的结果。STARFISH自主水下航行器具有轻微的正浮力，但由于我们将固连体坐标系置于浮心处，浮力在方程中不起作用。由静水扶正力矩产生的横摇力矩为
$$
τ_{Hydro}= −ygW \cosφ+ zgW \sinφ. \tag{2}
$$

IRM 被视为一个距离中心有效长度为 l 的质点。有效长度 l 是从 CB 到尾部托盘 CG 的距离。设 α 表示如图2(b)所示的质点的角位置。当该质点在 AUV 内部滚转时，实际上改变了 AUV 的重心。新的重心位置（y′g,z′g）由以下两个方程描述：
$$
y′_g= y_g+ \frac{m}{M} l \sinα \tag{3}
$$
$$
z′_g= z_g − \frac{m}{M} l \cosα \tag{4}
$$
其中 m 是尾部托盘质量，M 是整个AUV的质量。

通过将 (3) 和 (4) 代入 (2)，静水扶正力矩变为
$$
τ_{Hydro}= −(y_g+ \frac{m}{M} l \sinα)W \cosφ+(z_g− \frac{m}{M} l \cosα)W \sinφ. \tag{5}
$$

值得注意的是，静水力矩能够稳定滚转运动，因为该力矩始终抵抗任何横滚偏转。因此，在这个意义上滚转动力学是自稳定的。

3.2 滚动阻力

作为流线型AUV，STARFISH自主水下航行器的主要滚动阻力来自从中心轴突出的四个鳍。我们将该阻力建模为二次型阻力：
$$
τ_{Drag}= K_{pp}p|p| \tag{6}
$$
其中 Kpp是横滚二次型阻力系数，p是横摇角速度。由于我们仅在横滚轴上进行讨论，因此有 p= φ˙。

3.3 横滚附加质量

附加质量是衡量车辆加速时运动的水的质量的指标。对于流线型AUV，由于 AUV艇体产生的横滚附加质量较小，因此主要的横滚附加质量仍由鳍产生。我们将附加质量引起的力矩建模如下：
$$
τ_{AM}= K_{p ˙} p˙ \tag{7}
$$
其中Kp ˙为滚转附加质量系数， ˙p为滚转角加速度。类似地，我们有 ˙p= φ¨。

3.4 螺旋桨引起的扭矩

当螺旋桨顺时针旋转以提供正向推力时，也会在自主水下航行器上产生一个逆时针方向的力矩。这通常被称为力矩效应。该力矩的大小取决于推进器的功率输出P和螺旋桨转速 ω，如以下公式所示：
$$
τ_{prop}= \frac{P}{ω}. \tag{8}
$$
推进器产生的功率是推力F与自主水下航行器速度V的乘积。然而在稳态（恒定速度）运动时，推力等于阻力Fdrag，因此
$$
P= FV= F_{drag}V \tag{9}
$$
$$
F_{drag}= \frac{1}{2}ρAC_dV^2 \tag{10}
$$
其中ρ为海水密度；A为迎流面积；Cd为阻力系数。因此，通过进行不同恒定推力实验，我们在图3中绘制了诱导力矩与螺旋桨转速的关系。数据最符合一个二次方程，显示 τprop ∝ ω²。

在后续分析中，我们忽略诱导力矩，并将其视为系统扰动。然而，在配重调整过程中，我们对自主水下航行器进行预滚转至+5◦，以补偿标称速度下的推进器力矩。当自主水下航行器以1.4米/秒的标称速度和1400 转/分钟运行时，诱导力矩会将自主水下航行器恢复至零滚转位置，从而为内部移动质量补偿其余变化留出足够的调节空间。

将(5)、(6)、(7)和(8)代入(1)并重新整理各项，可得
$$
(I_{xx} −K_{p ˙})φ ¨= −(y_g+ \frac{m}{M} l \sinα)W \cosφ +(z_g − \frac{m}{M} l \cosα)W \sinφ +K_{pp}p|p| +τ_{prop}. \tag{11}
$$

我们通过在工作点 φ= 0处对(11)进行线性化，得到横滚的传递函数φ关于 α的表达式，如(12)所示。在此工作点，cosφ ≈ 1和sinφ ≈ φ中的α可假设为很小量，因此cosα ≈ 1和sinα ≈ α。接下来，我们将二次型阻力Kppp|p|近似为线性阻尼Kpp。根据配平条件，yg接近零点，因而被忽略。最后， τprop被视为扰动，不包含在方程中。

$$
\frac{φ}{α}= \frac{−[\frac{(m)}{M}lW]}{I_{xx} −K_{p ˙}} \cdot \frac{s^2 −[ \frac{K_p}{I_{xx} −K_{p ˙}} ] s−[\frac{(z_g −\frac{(m)}{M}l)W}{l_{xx} −K_{p ˙}}]}{}. \tag{12}
$$

通过将常数参数k、a和b分别赋给其对应的系数，(12)变为：
$$
\frac{φ}{α}= \frac{k}{s^2+ as+ b}. \tag{13}
$$

4 系统辨识

在本节中，我们估计了式（13）中提出的线性二阶横滚轴模型的三个未知参数a、b和k。同时，我们也辨识非线性方程（11）中的Kp ˙、Kpp和l。其他参数，例如Ixx、yg、zg、m、M、W，可通过直接测量或通过计算机辅助设计 （CAD）软件进行计算。这些参数的数值列于表1中。

通常，我们需要通过在±20◦之间使用阶跃函数改变 α来进行开环测试，然后记录横滚响应。理想情况下，应在自主水下航行器保持恒定推力、深度和航向时进行该测试，以最小化由这些自由度产生的耦合扭矩。然而，由于我们正在测试滚转动力学的一些未知行为，开环测试可能对自主水下航行器的运行构成危险。一个更自然的选择是在自主水下航行器静止于水箱中时进行开环测试。这实际上已足以获得滚转动力学的标称模型，原因如下：首先，在我们的模型中，我们将推进器诱导力矩视为一种干扰，因此无论推进器是否运行，它都不会被包含在模型中。

当自主水下航行器在水箱中静止时，我们施加三个幅值为 α（‐20◦、 0◦和 20◦）的阶跃输入，并观察横滚对 α阶跃变化的响应。每次阶跃变化前均留有足够时间使横滚响应衰减完毕。结果如图4所示。仿真横滚响应与实验测得的横滚响应叠加显示，两者吻合良好。仿真横滚由未知参数经辨识后的非线性模型生成。3个未知参数通过数值最小化如下定义的均方根误差 φrms得到：
$$
Φ_{rms}=\sqrt{ \frac{\sum_{i=1}^{n}(φ_i− \hat{φ}_i)^2}{n} }. \tag{14}
$$
其中φ为仿真横滚响应，n为样本数量。采用Nelder‐Mead单纯形法在最小二乘意义下搜索最优参数集。

需要注意的是， α是给伺服电机的指令。没有仪器可以测量滚动质量的位置。因此，指令的α与实际的 α之间会存在一定的延迟。我们用时间常数为 τdelay的一阶系统来建模该延迟。为了辨识该时间常数，我们通过在±20◦之间随机指令α进行动态测试，以获得图5所示的响应。类似地，通过最小化 φrms来辨识时间常数。最终得到的传递函数(13)为：
$$
\frac{φ}{α}=\left( \frac{1}{τ_{delay} s+ 1}\right)\left( \frac{k}{s^2+ as+ b} \right) \tag{15}
$$
当 τdelay = 0.5 s 时。

5 控制器设计

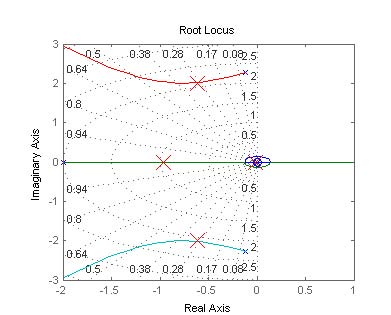
在本节中，我们设计了一种比例‐积分（PI）控制器，用于稳定自主水下航行器的横滚运动。该PI控制器通过增加系统的阻尼来减小横滚振荡，同时保持零稳态误差。控制器基于根轨迹设计合成（图6）。

开环传递函数在s平面的虚轴附近有一对共轭复数极点。这表明系统的阻尼较弱，阻尼比为0.07。图6还显示，系统仅在根轨迹的一小部分区域内稳定；其在闭环增益范围（0< Kp< 8.50）内稳定。该稳定区域似乎也具有较弱的阻尼特性。通过增大增益，可使这对共轭复数极点移至阻尼较高的区域。然而，随着增益的增加，第三个极点逐渐接近右半平面。由于这些极点彼此靠近，我们无法单纯基于二阶近似来分析系统。因此，我们通过仿真非线性模型，并利用仿真结果对控制器增益进行精细调节。添加了一个理想的积分环节，在0.01处设置了一个零点。第四个闭环极点位于‐0.0144。

接近零点，导致极点-零点相消。开环和闭环系统的所有极点和零点均列于表2中。通过防止积分项在 20◦之上或之下累积，避免了积分饱和。

6 结果与讨论

通过水槽试验和野外试验，首先研究了内部滚动质量在控制横滚方面的性能。在水槽试验中，我们通过推动自主水下航行器使其横滚至{v1}，施加一个脉冲并分别观察开环和闭环控制下横滚衰减的情况。结果如图7所示。闭环响应在4秒内稳定，而开环系统则需要超过10秒才能稳定。图7还显示了 α随时间变化以抑制横滚的情况。在开环试验中， α保持在恒定值0◦。

图8显示了自主水下航行器在以1.4米/秒的速度沿直线路径执行恒定2米下潜任务期间的横滚响应。当内部移动质量机构关闭（开环）时，自主水下航行器的横滚响应呈现振荡性，标准差为 1.02◦。相反，当内部移动质量机构开启（闭环）时，振荡性横摇运动被抑制。移动质量向负阿尔法区域滚动，以抵消螺旋桨扭矩的影响。横滚的标准差降低至 0.393◦。表3将测试结果总结为两个统计量：均值和标准差。从均值来看，内部移动质量机构还使振荡以零角度为中心。总之，结果表明，内部移动质量机构将不希望出现的横滚振荡抑制到更小的幅度，并围绕零点中心化。

7 结论

我们展示了在尾部推进且鳍控制的自主水下航行器（AUV）中使用内部滚动质量机构（IRM机构）实现主动滚转稳定的方法。该机构已在STARFISH自主水下航行器（STARFISH AUV）上进行了设计与实现。首先建立了一个非线性模型以描述自主水下航行器滚转运动的动力学特性，随后对该模型进行线性化处理，得到用于控制器综合的传递函数。通过在水箱中进行开环测试，对模型的参数进行了辨识。接着设计了PI控制器，以提高系统的整体阻尼并消除稳态误差。通过水槽试验和野外试验验证了内部滚动质量（IRM）稳定滚转运动的能力。