79.单词搜索 python

最新推荐文章于 2025-12-12 14:50:02 发布

原创最新推荐文章于 2025-12-12 14:50:02 发布 · 658 阅读

8 ·

CC 4.0 BY-SA版权

文章标签：

#python #开发语言 #矩阵 #线性代数 #数据结构 #面试 #leetcode

leetcode面试经典150题专栏收录该内容

129 篇文章

订阅专栏

单词搜索

题目
题解
- 进阶优化：搜索剪枝
- 提交结果

题目

题目描述

给定一个 m x n 二维字符网格 board 和一个字符串单词 word 。如果 word 存在于网格中，返回 true ；否则，返回 false 。

单词必须按照字母顺序，通过相邻的单元格内的字母构成，其中“相邻”单元格是那些水平相邻或垂直相邻的单元格。同一个单元格内的字母不允许被重复使用。

示例 1：

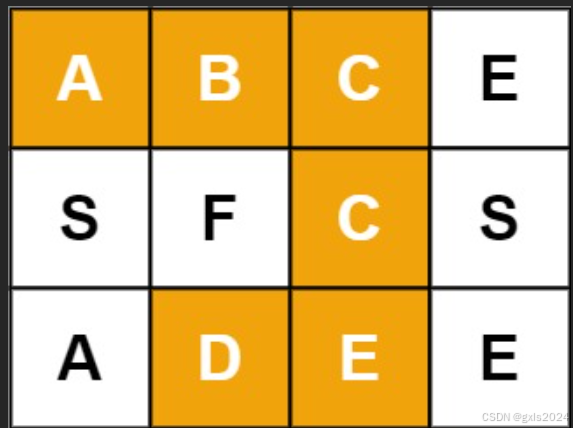
在这里插入图片描述

输入：board = [[“A”,“B”,“C”,“E”],[“S”,“F”,“C”,“S”],[“A”,“D”,“E”,“E”]], word = “ABCCED”
输出：true

示例 2：

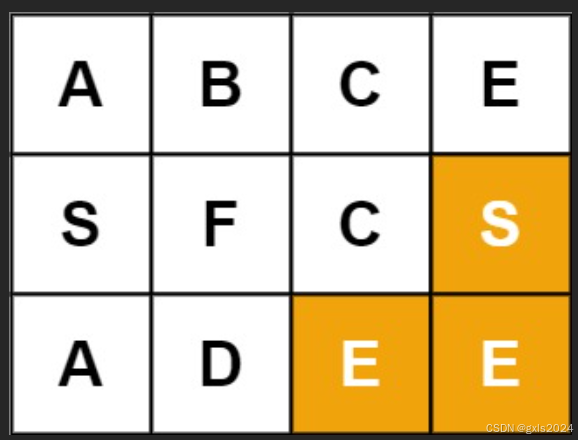
在这里插入图片描述

输入：board = [[“A”,“B”,“C”,“E”],[“S”,“F”,“C”,“S”],[“A”,“D”,“E”,“E”]], word = “SEE”
输出：true

示例 3：

在这里插入图片描述

输入：board = [[“A”,“B”,“C”,“E”],[“S”,“F”,“C”,“S”],[“A”,“D”,“E”,“E”]], word = “ABCB”
输出：false

提示：

m == board.length
n = board[i].length
1 <= m, n <= 6
1 <= word.length <= 15
board 和 word 仅由大小写英文字母组成

进阶：你可以使用搜索剪枝的技术来优化解决方案，使其在 board 更大的情况下可以更快解决问题？

题解

这个问题可以通过深度优先搜索（DFS）来解决。对于每个起始点，我们尝试沿着四个方向（上、下、左、右）进行递归搜索，检查是否可以找到匹配的单词路径。为了避免重复使用同一个单元格，我们需要在进入递归时标记当前单元格为已访问，并在退出递归时恢复其状态。

以下是 Python 实现：

def exist(board, word):
    if not board or not board[0]:
        return False

    rows, cols = len(board), len(board[0])

    def dfs(r, c, index):
        # 如果索引达到了单词的长度，说明已经找到了完整的单词
        if index == len(word):
            return True

        # 检查边界条件和字符匹配
        if r < 0 or r >= rows or c < 0 or c >= cols or board[r][c] != word[index]:
            return False

        # 标记当前单元格为已访问
        temp, board[r][c] = board[r][c], '#'

        # 尝试向四个方向递归搜索
        found = (dfs(r + 1, c, index + 1) or
                 dfs(r - 1, c, index + 1) or
                 dfs(r, c + 1, index + 1) or
                 dfs(r, c - 1, index + 1))

        # 恢复当前单元格的状态
        board[r][c] = temp

        return found

    # 尝试从每个单元格开始搜索
    for r in range(rows):
        for c in range(cols):
            if dfs(r, c, 0):
                return True

    return False