洛谷 P1364 医院设置题解

原创于 2025-08-05 21:02:26 发布 · 931 阅读

17 ·

CC 4.0 BY-SA版权

文章标签：

#算法

题解专栏收录该内容

11 篇文章

订阅专栏

P1364 医院设置

完整题目

P1364 医院设置

题目描述

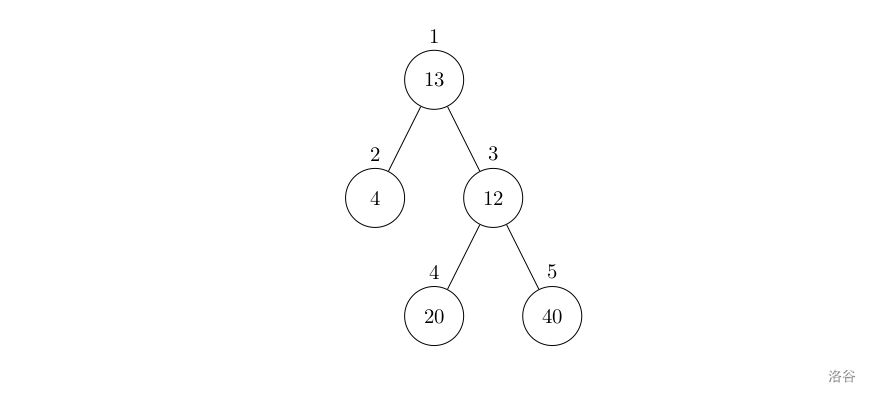
设有一棵二叉树，如图：

其中，圈中的数字表示结点中居民的人口。圈边上数字表示结点编号，现在要求在某个结点上建立一个医院，使所有居民所走的路程之和为最小，同时约定，相邻接点之间的距离为 $1$ 。如上图中，若医院建在 $1$ 处，则距离和 $=4+12+2×20+2×40=136=4+12+2\times20+2\times40=136$ ；若医院建在 $3$ 处，则距离和 $=4×2+13+20+40=81=4\times2+13+20+40=81$ 。

输入格式

第一行一个整数 $n$ ，表示树的结点数。
接下来的 $n$ 行每行描述了一个结点的状况，包含三个整数 $w, u, v$ ，其中 $w$ 为居民人口数， $u$ 为左链接（为 $0$ 表示无链接）， $v$ 为右链接（为 $0$ 表示无链接）。

输出格式

一个整数，表示最小距离和。

输入输出样例 #1

输入 #1
5						
13 2 3
4 0 0
12 4 5
20 0 0
40 0 0
输出 #1
81
说明/提示

数据规模与约定

对于 $100%100\%$ 的数据，保证 $\leq n \leq 100$ ， $\leq u, v \leq n$ ， $\leq w \leq 10^5$ 。

题意

题目中写的： $=4+12+2×20+2×40=136=4+12+2\times20+2\times40=136$ 改为： $=4×1+12×1+2×20+2×40=136=4\times1+12\times1+2\times20+2\times40=136$ 更严谨。
大部分人可能看懂题目了，我再说一遍，看懂的可以跳过。
在一个二叉树里找一个点，使得所有点的 $权值×层数权值\times层数$ 之和为最小，然后输出最小和。

算法：树形DP+DFS暴力枚举

树形 DP，即在树上进行的 DP。由于树固有的递归性质，树形 DP 一般都是递归进行的。
$\hspace{11cm}$ ——OIwiki
枚举的思想是不断地猜测，从可能的集合中一一尝试，然后再判断题目的条件是否成立。
$\hspace{11cm}$ ——OIwiki

那么如何实现这两个算法呢？我们可以把树形DP套进DFS函数里，然后在进行调用，暴力枚举。
那如果这样，我们可以先把数据存到一个无向图里，然后通过遍历DFS图来进行解题，DFS遍历的时候，每次都历当前节点相联通的所有节点，如果其他相联通的所有节点本次未被访问过，那就标记一个特定值（每层都不一样），意义为“本次层遍历访问过”。然后累加人口距离到总和中，递归搜索相联通的节点，距离+1。

是不是听着代码比较容易写？（个人觉得比较好写）这个思路的优点就是代码容易实现，缺点显而易见，可能超时，不过数据较水，可以跑。

然后就是建图的问题了，这里建议使用邻接表建图法，建议用vector<int>g[]，比较方便，如果存在右子节点，建立双向关连g[i].push_back(y);g[y].push_back(i)。如果存在左子节点，建立双向关连g[i].push_back(x);g[x].push_back(i).

代码实现

变量定义：

int a[1000005];//存储每个节点的人口数
int f[1000005];//访问标记数组，用于DFS时记录节点是否被访问过
vector<int>g[1000005];//邻接表，存储树的连接关系
int ans=INT_MAX;
int cnt,n;
//cnt:临时累计值
//n:节点总数

DFS（树形DP部分）：

void dfs(int x,int sum,int d){
//x:当前节点
//sum:当前距离
//d:本次搜索标记值
	for(int i=0;i<g[x].size();i++){//遍历当前节点相联通的所有节点 
		if(f[g[x][i]]!=d){//如果其他相联通的所有节点本次未被访问过  
			f[g[x][i]]=d;//标记为已访问，使用d值区分不同搜索 
			cnt+=a[g[x][i]]*sum;//累加人口距离到总和中
			dfs(g[x][i],sum+1,d);//递归搜索邻居节点，距离+1
		}
	}
}

主函数（枚举部分）：

	cin>>n;
	for(int i=1;i<=n;i++){
		cin>>a[i];
		int x,y;
		cin>>x>>y;
		if(x!=0){//如果存在左子节点
    		g[i].push_back(x);//建立双向关连
			g[x].push_back(i);
		} 
		if(y!=0){//如果存在右子节点
			g[i].push_back(y);//建立双向关连
			g[y].push_back(i);		
		}		
	}
	for(int i=1;i<=n;i++){//枚举每个节点作为医院 
		cnt=0;//清零累加器
		f[i]=i;//标记起始节点，使用i作为本次搜索标记值
		dfs(i,1,i);//从节点i开始DFS，初始距离1，标记值i
		ans=min(ans,cnt);//更新答案 
	}
	cout<<ans;