PD控制器参数选择
见书第117到119页:
对于图6-21所示系统。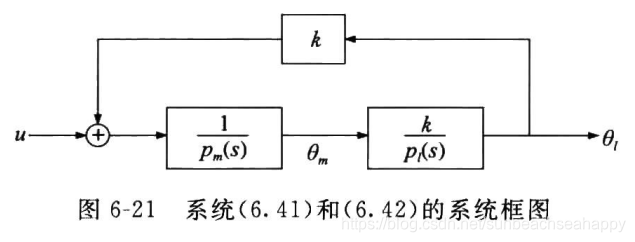
其传递函数为
(1)
Θ
l
(
s
)
U
(
s
)
=
k
p
l
(
s
)
p
m
(
s
)
−
k
2
\frac{\Theta_l(s)}{U(s)}=\frac{k}{p_l(s)p_m(s)-k^2} \tag{1}
U(s)Θl(s)=pl(s)pm(s)−k2k(1)
在实践中,由于谐波齿轮的刚度较大而阻尼较小,这会使系统难以控制。假设我们采用一个PD型控制器
C
(
s
)
=
K
P
+
K
D
s
C(s)=K_P+K_Ds
C(s)=KP+KDs。此时我们分别分析传感器检测电机轴或者负载轴的两种不同情况
对于上述两种情况,我们分析其根轨迹,故设
K
P
+
K
D
s
=
K
D
(
s
+
a
)
K_P+K_Ds=K_D(s+a)
KP+KDs=KD(s+a)其中
a
=
K
P
/
K
D
a=K_P/K_D
a=KP/KD
情况一、采用电机转角作为反馈的PD控制
框图如下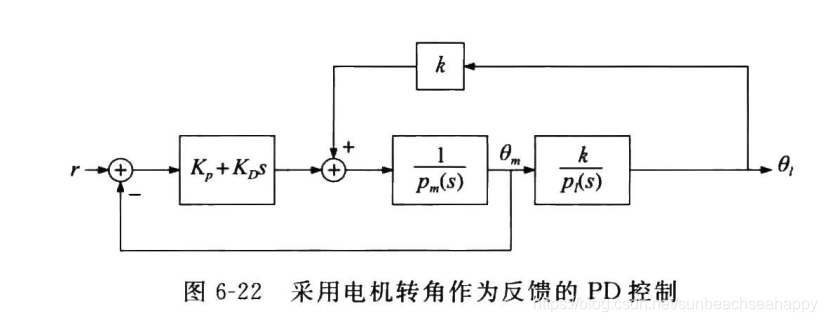
易知其闭环传递函数为:
(2)
Θ
l
(
s
)
R
(
s
)
=
K
D
(
s
+
a
)
k
p
m
(
s
)
p
l
(
s
)
−
k
2
+
K
D
(
s
+
a
)
p
l
(
s
)
\frac{\Theta_l(s)}{R(s)}=\frac{K_D(s+a)k}{p_m(s)p_l(s)-k^2+K_D(s+a)p_l(s)} \tag{2}
R(s)Θl(s)=pm(s)pl(s)−k2+KD(s+a)pl(s)KD(s+a)k(2)
所以开环传递函数为
(3)
G
(
s
)
H
(
s
)
=
K
D
(
s
+
a
)
p
l
(
s
)
p
m
(
s
)
p
l
(
s
)
−
k
2
G(s)H(s)=\frac{K_D(s+a)p_l(s)}{p_m(s)p_l(s)-k^2} \tag{3}
G(s)H(s)=pm(s)pl(s)−k2KD(s+a)pl(s)(3)
我们假定
{
J
l
=
1
B
l
=
0.1
J
m
=
1
B
m
=
0.1
k
=
60
a
=
1
\left\{ \begin{matrix} J_l = 1 & B_l=0.1 \\ J_m = 1 & B_m = 0.1 \\ k=60 \\ a=1 \end{matrix} \right.
⎩⎪⎪⎨⎪⎪⎧Jl=1Jm=1k=60a=1Bl=0.1Bm=0.1
使用MATLAB计算得根轨迹图为
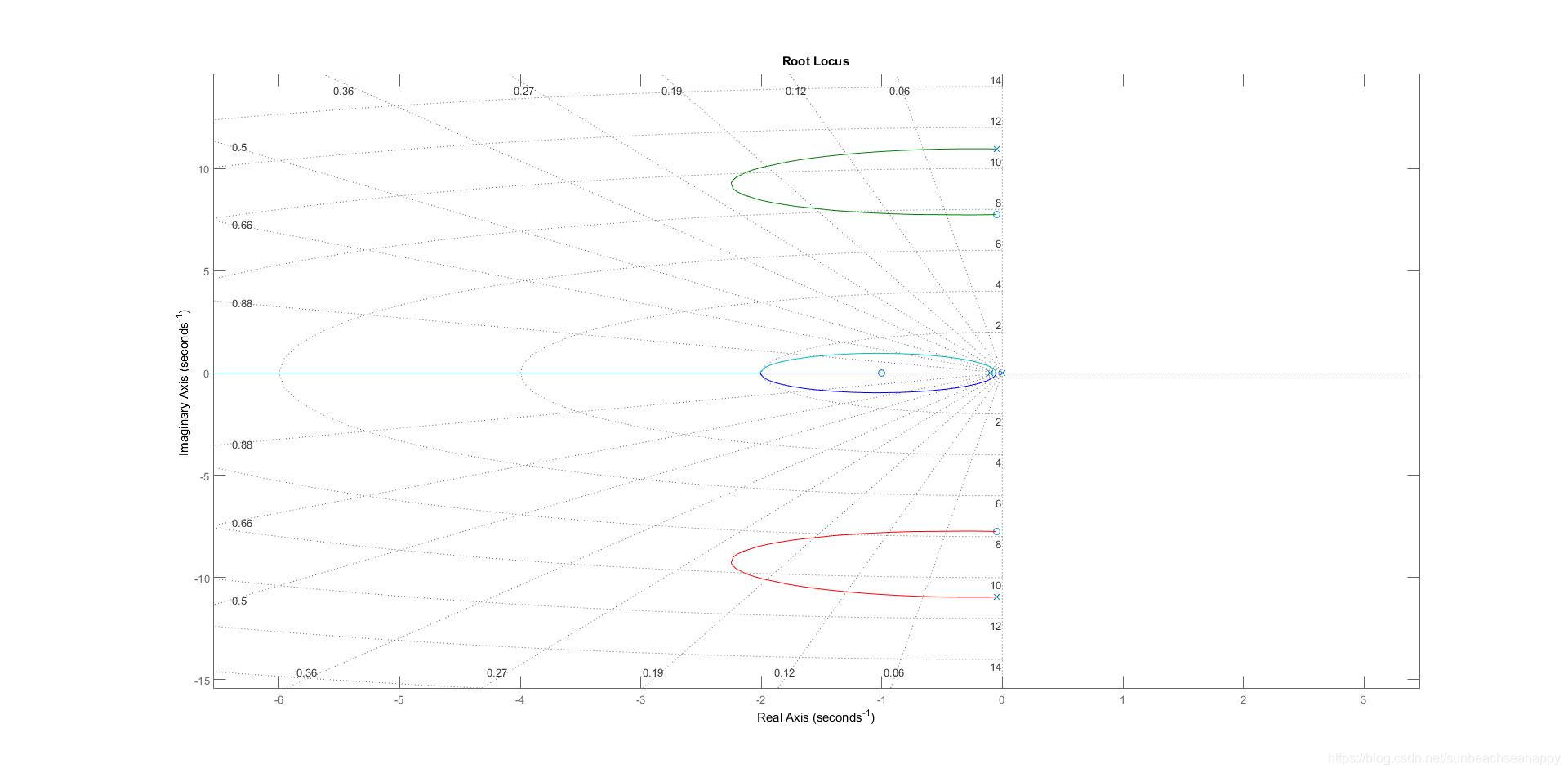
情况二、采用负载转角作为反馈的PD控制
框图如下:
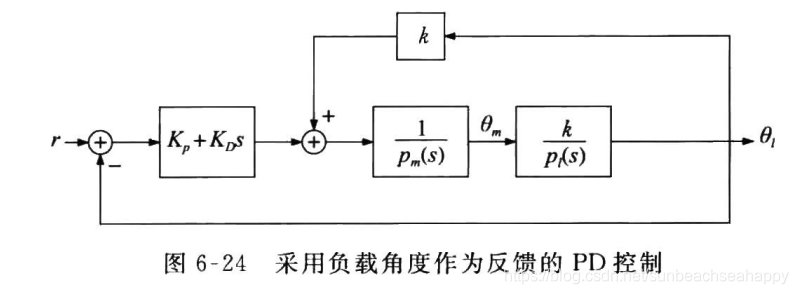
其开环传递函数易知:
(4)
Θ
l
(
s
)
R
(
s
)
=
K
D
(
s
+
a
)
k
p
m
(
s
)
p
l
(
s
)
−
k
2
\frac{\Theta_l(s)}{R(s)}=\frac{K_D(s+a)k}{p_m(s)p_l(s)-k^2} \tag{4}
R(s)Θl(s)=pm(s)pl(s)−k2KD(s+a)k(4)
参数假定同情况一,用MATLAB绘制根轨迹为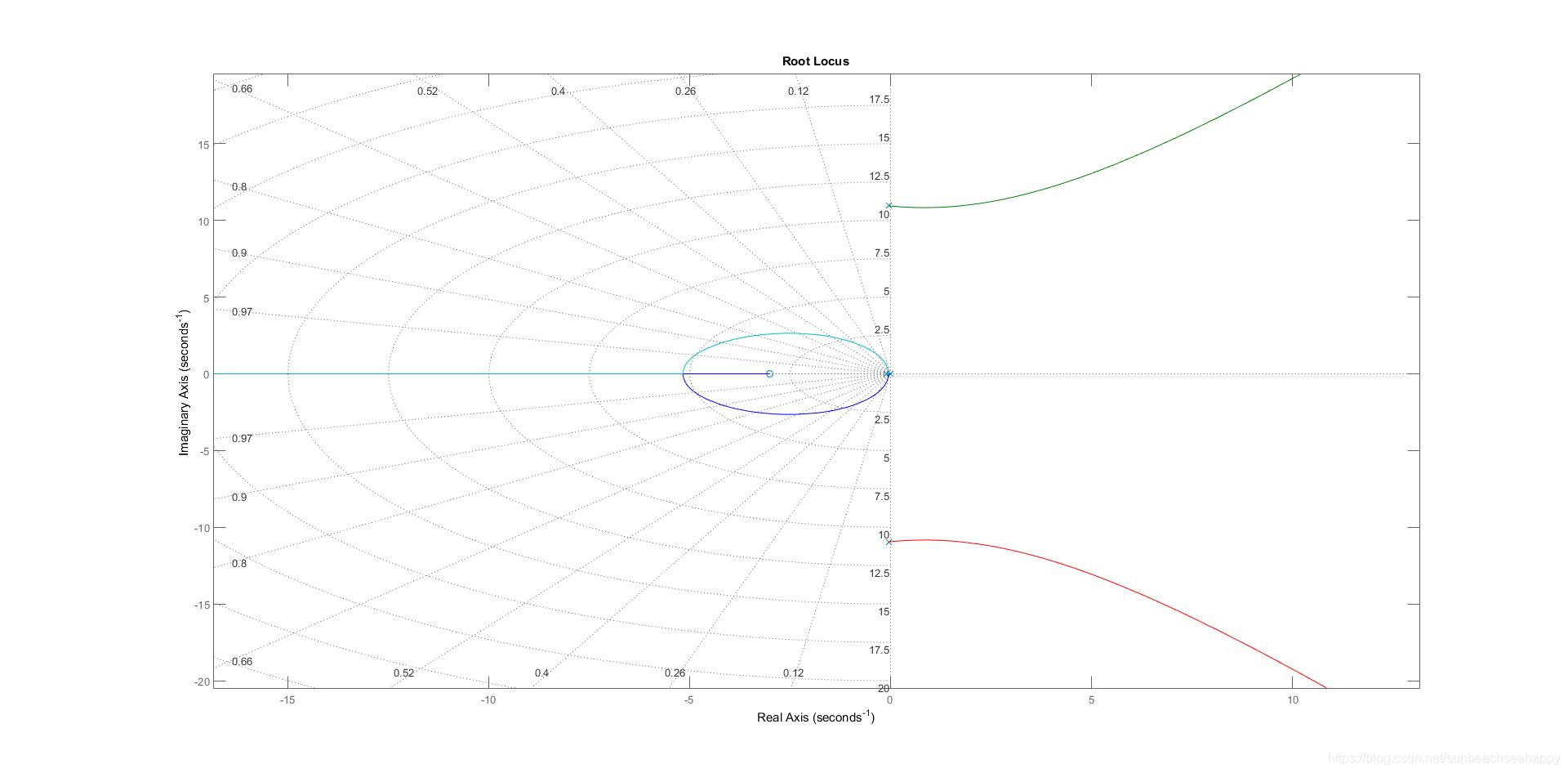







 博客围绕PD控制器参数选择展开,考虑谐波齿轮刚度大、阻尼小使系统难控制的情况,采用PD型控制器。分别分析传感器检测电机轴和负载轴两种情况,给出闭环和开环传递函数,并假定参数,用MATLAB绘制根轨迹。
博客围绕PD控制器参数选择展开,考虑谐波齿轮刚度大、阻尼小使系统难控制的情况,采用PD型控制器。分别分析传感器检测电机轴和负载轴两种情况,给出闭环和开环传递函数,并假定参数,用MATLAB绘制根轨迹。
















 712
712

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








