RRT、双向RRT和A*算法的简单总结

之前学习了一下路径规划算法，一直想总结一下，但是一直因为各种事情推迟，今天趁着比较闲，稍微总结一下。

传统RRT算法

原理：对于起点和目标点，从起点开始，通过随机采样获取一个采样点，判断是否满足连接条件，如果满足，将该点加入路径之中，重新进行采样，直到最后一个采样点在目标区域附近，结束。

通过随机采样增长一棵树，直到树覆盖了整个自由空间或达到了目标区域。

传统RRT算法步骤：

1. 创建一个树节点结构体数组，初始时加入起始坐标和目标坐标；

2. 在地图上生成随机采样点，生成公式如下：
   $$\begin{gathered} x_{random}=q\cdot x_{map} \\ {y}_{random}=q\cdot y_{map} \end{gathered}$$
   其中，$(x_{random},y_{random})$为随机点的x轴坐标与y轴坐标，q为0到1之间的一个随机数，$(x_{map},y_{map})$为地图的横坐标与纵坐标的大小。

3. 新产生的随机点与结构体数组中的每个节点进行距离比较，选取距离最小的作为其父节点，并依据父节点和随机点的方向，按照一个固定的步长确定新节点的位置。公式如下：
   $$\begin{array}{rl}D(i)& =\sqrt{(x_{random}-x_i{)}^2+(y_{random}-y_i{)}^2}\\ \alpha & =\arctan \left(\frac{y_{random}-y_i}{x_{random}-x_i}\right)\\ x_{new}& =x_i+step\times \cos (\alpha )\\ y_{new}& =y_i+step\times \sin (\alpha )\end{array}$$

   式中: $(x_i,y_i) $为结构体数组中的第i个节点，$D(i)$为随机点与结构体数组中第i个节点的距离值; $\alpha$为随机点与最近临近节点之间的角度值; $step$为新节点的固定扩展步长; $(x_{new},y_{new})$为产生的新节点坐标。

4. 对新节点进行碰撞检测：若新节点不在障碍物范围内且与父节点之间的连接线没有与障碍物边界发生接触，则表示采样成功；当新节点与终点节点之间的距离小于预先设置的阈值时，路径搜索工作完成，将终点纳入到结构体数组。对结构体数组中的节点信息进行回溯处理，得到初始路径。

算法拓展图如下图所示：

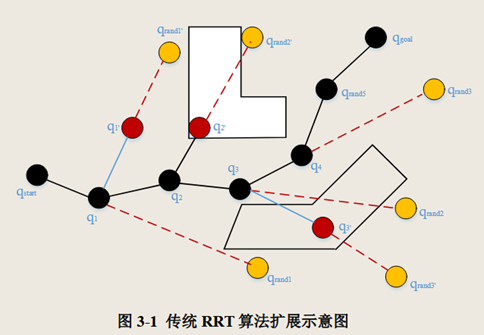
双向RRT算法

双向RRT算法就是在传统RRT算法的基础上改进而来，引入两棵树同时进行扩展的策略。

双向RRT算法的步骤:

1. 创建两个树状结构体数组，初始时，起点和终点分别加入其中一个。
2. 在地图上生成采样点，计算该点两棵树中所有节点的距离，选择距离最小的点作为其父节点。
3. 依据采样点和父节点的方向，按照一个固定步长确定新节点Q1的位置；同时，对于另一棵树，找到其中与新节点Q1最近的节点P1，依据P1与Q1的方向，按照一个固定步长确定另一棵树新节点Q2的位置
4. 对两棵树中的新节点Q1，Q2进行碰撞检测，若无碰撞，则分别加入两棵树中；若碰撞，舍弃该新节点。重复步骤2-4
5. 当两棵树的新节点之间的距离小于或等于单个步长时，结束搜索

A*算法

摘自文章：https://zhuanlan.zhihu.com/p/54510444

A*算法通过一个函数来计算每个节点的而优先级，通过每次选择优先级最高的节点，作为下一个待遍历的节点。

函数如下：$f(n)=g(n)+h(n)$，对于这个函数，其中：

• $f(n)$: 节点n的综合优先级。当我们选择下一个要遍历的节点时，我们总会选取综合优先级最高（值最小）的节点。
• $g(n) $是节点n距离起点的代价。
• $h(n)$是节点n距离终点的预计代价，这也就是A*算法的启发函数。

启发函数

启发函数会影响A*算法的行为

• 在极端情况下，当启发函数h(n)始终为0，则将由g(n)决定节点的优先级，此时算法就退化成了Dijkstra算法。
• 如果h(n)始终小于等于节点n到终点的代价，则A*算法保证一定能够找到最短路径。但是当h(n)的值越小，算法将遍历越多的节点，也就导致算法越慢。
• 如果h(n)完全等于节点n到终点的代价，则A*算法将找到最佳路径，并且速度很快。可惜的是，并非所有场景下都能做到这一点。因为在没有达到终点之前，我们很难确切算出距离终点还有多远。
• 如果h(n)的值比节点n到终点的代价要大，则A*算法不能保证找到最短路径，不过此时会很快。
• 在另外一个极端情况下，如果h()n相较于g(n)大很多，则此时只有h(n)产生效果，这也就变成了最佳优先搜索。

由上面这些信息我们可以知道，通过调节启发函数我们可以控制算法的速度和精确度。因为在一些情况，我们可能未必需要最短路径，而是希望能够尽快找到一个路径即可。这也是A*算法比较灵活的地方。

对于网格形式的图，有以下这些启发函数可以使用：

• 如果图形中只允许朝上下左右四个方向移动，则可以使用曼哈顿距离。
• 如果图形中允许朝八个方向移动，则可以使用对角距离。
• 如果图形中允许朝任何方向移动，则可以使用欧几里得距离。

完整A*算法描述如下：

* 初始化open_set和close_set；
* 将起点加入open_set中，并设置优先级为0（优先级最高）；
* 如果open_set不为空，则从open_set中选取优先级最高的节点n：
    * 如果节点n为终点，则：
        * 从终点开始逐步追踪parent节点，一直达到起点；
        * 返回找到的结果路径，算法结束；
    * 如果节点n不是终点，则：
        * 将节点n从open_set中删除，并加入close_set中；
        * 遍历节点n所有的邻近节点：
            * 如果邻近节点m在close_set中，则：
                * 跳过，选取下一个邻近节点
            * 如果邻近节点m也不在open_set中，则：
                * 设置节点m的parent为节点n
                * 计算节点m的优先级
                * 将节点m加入open_set中