一、符号扩展
定点数表示的数转换成具有不同位数的某种表示形式。整数的符号扩展在首,小数的符号扩展在尾。其根本目的是:表示的数值保持不变。
- 对于正数,新表示形式的所有附加位都用0进行填充
- 对于负数
- 符号位保持不变,原码的所有附加位都用0进行填充
- 符号位保持不变,反码的所有附加位都用1进行填充
- 符号位保持不变,补码的所有附加位都用1(对于整数)或0(对于小数)进行填充

二、溢出判断
方法一:采用一位符号法
当参加操作的两个数符号相同,结果又与原操作数符号不同,则表示结果溢出。

方法二:采用双符号位
最高位符号位表示真正的符号,次高位符号位表示操作数的进位

- S1S2=00,表示结果为正数,无溢出
- S1S2=01,表示结果正溢出(当两个正数相加)
- S1S2=10,表示结果负溢出(当两个负数相加)
- S1S2=11,表示结果为负数,无溢出
方法三:采用一位符号位根据数据位的进位情况判断溢出
若符号位的进位 Cs 与最高数位的进位 C1 相同,则说明没有溢出(相当于00,11),否则发生溢出(相当于01,10)
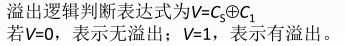
























 1072
1072

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








