总
上次我们把二叉树的性质和概念,代码实现全部完结。所以这篇我们来趁热打铁,写几道二叉树的经典面试题,我会尽我的能力把题目思路和代码实现谈清楚,如果对二叉树的性质这些的不清楚的可以看二叉树的性质和实现-优快云博客进行一些复习和巩固。正片开始我们先看看本篇要讲的面试题,这些题目都是从简单到难的,前四题一个档次,后三题就需要你的智商在线了。
1. 检查两棵树是否相同。
2. 另⼀棵树的子树。
3. 翻转⼆叉树。
4. 对称⼆叉树。
5. 给定⼀个⼆叉树,找到该树中两个指定节点的最近公共祖先。
6. 根据⼀棵树的前序遍历与中序遍历构造⼆叉树。
7. ⼆叉树中序非递归遍历实现。
第一题
检查二棵树是否相同,100. 相同的树 - 力扣(LeetCode)
我们想要判断两课二叉树是不是相同的,是不是就要判断他们是不是相同的就好了(听不懂就跳过这句话)我们判断两棵树是不是相同,你可以想到什么方法,反正我就想到了,看根节点是不是相同再看左子树最后看右子树(你想先看右子树好像也可以,题是死的,人的活的,你总不能被尿憋死吧)那我们又要想了,我们怎么判断左右子树是不是相同的呢,还不是根节点,左子树,右子树,这样一想,就知道了写一个递归阿,都是这样一直判断下去嘛,如果一直判断到左子树右子树都为空了还是一样的,那就是相同了嘛,那假如我们发现了不同的(那恭喜了您嘞,玩完了)我们直接反正false就好了。但是还有一个要注意的点,因为我们不知道他们传的是不是一个空的二叉树,所以我们在开头的时候,要先判断一下啊,结果还刚好,把我们递归停下的地方写好了,思路完成,我们看代码。
if(p == null && q == null){
return true;
}
if(p == null || q == null){
return false;
}
if(p.val == q.val){
boolean left = isSameTree(p.left,q.left);
boolean right = isSameTree(p.right,q.right);
return left && right;
}else{
return false;
}
 欧克了,来下一个。
欧克了,来下一个。
第二题
另⼀棵树的子树,这个我们看题目好像不说写的很清楚,所以我们进来看看572. 另一棵树的子树 - 力扣(LeetCode)就基本理解题目了,就是给我们两棵树(一课我们叫母树,还有一课叫子树,子树是母树的一个枝干),我们看看一棵树是不是另一课树的子树,其实这个题应该思路一下就出来了,我们先找到子树的根节点的值会不会等于母树上那个节点的值,假如说找到了,那这个母树这个节点的树就是和子树一样,那我们没有找到怎么办,你说,不是更好啊,连根节点的值都不一样,你觉得还有判断的必要吗,那肯定是找不到啊,所以说大方向我们找好了,但是我们要想好每一个细节,来想想还有没有什么我们没有考虑到的,对对对,就是找到了,下面怎么实现,很简单就是判断两个子树是否相同啊(那这个怎么写啊,好难想啊),不就是第一题啊,那我们可以实现了不,其实还有一个小漏洞,就是我们找到了,但是这个节点的树和二叉树不一样,然后下面还有一个值等于子树的节点,这个漏洞也好解决,就是继续向下递归呗,找到了,就返回true,一个树都找完了都找不到就返回false就好了,思路就这么多,我们来看代码
public boolean isSubtree(TreeNode root, TreeNode subRoot) {
if(root == null && subRoot == null){
return true;
}
if(root == null || subRoot == null){
return false;
}
if(root.val == subRoot.val){
if(isSameTree(root,subRoot) == true){
return true;
}else{
boolean left = isSubtree(root.left,subRoot);
boolean right = isSubtree(root.right,subRoot);
return (left || right);
}
}else{
boolean left = isSubtree(root.left,subRoot);
boolean right = isSubtree(root.right,subRoot);
return (left || right);}
}但是我们还需要第一题的判断代码放一起就可以了。
第三题
翻转⼆叉树226. 翻转二叉树 - 力扣(LeetCode),这个题目一看就知道要干什么就是把一颗二叉树翻转一下就好了,左边的去右边,右边的来左边,中间的呢(我知道中间的去下面,你想出来了,你就是sb)中间的还在中间,我们的思路应该就很明确了,就是左边到右边不就好了,那我们来想一下,第一层就根节点,第二层就左子树和右子树(我们叫为左,右)对吧,他们两个交换一下,那第三层(是不是有左左,左右,右左,右右)呢,但是我们还是左右交换,左左和左右交换就好,不需要别的(看起来说了很多,实际上啥都没说,因为我们是递归啊牢弟,是从下往上的,但是思路还是一样的,)所以我们看代码。
public TreeNode invertTree(TreeNode root) {
if(root == null){
return null;
}
if(root.left == null && root.right == null){
return root;
}
if(root.left == null || root.right == null){
TreeNode count = root. left;
root.left = root.right;
root.right = count;
}
TreeNode left = invertTree(root.left);
TreeNode right = invertTree(root.right);
if(root.left != null && root.right != null){
TreeNode count = root. left;
root.left = root.right;
root.right = count;
return root;
}
return root;
} 成功下一个,是不是觉得自己又行了。
成功下一个,是不是觉得自己又行了。
第四题
对称⼆叉树101. 对称二叉树 - 力扣(LeetCode),这个有一个特别简单是思路来实现,就是我们把这个二叉树复制一份,翻转一下再对比两个二叉树是否相同(翻转二叉树,前面写了,判断二叉树是否相同我们前面也写了,嘻嘻)但是如果是这样我就不会拿出这题来了,所以我们不使用上面的代码实现,我们想想,我们判断一个二叉树是否对称,是不是就是判断第二层的左右子树是不是相同,那第三层就是左左和右右相同,左右和右左是否相同,那第四层呢(这样下去会潮掉(发疯的意思,不过是家乡话)),所以这个思路不行,但是又不是完全不行,你想想,我们到第三层的时候,把左左的子树看为是一个新的树直接和右右的子树比较不就好了,假如相同就返回true,不相同就ok了,找到不同了(道爷我成了)是不是,那就会有人想,为什么我们不是再第二层的时候把左和右传下去比较,因为
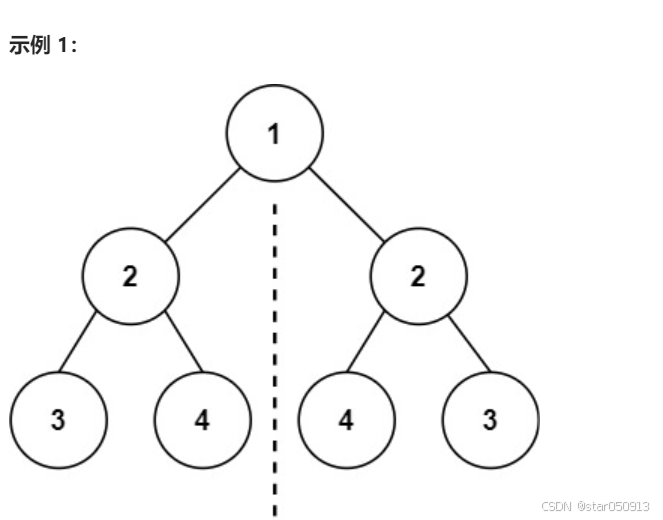
题中的实例1,2的左右子树传下去会一样吗,所以说我们只能使用第三层,不能使用第二层,那就会有人想了,我比到第四层行不行,我的评价是闲的蛋疼,第三层就好了,你非要多此一举,思路讲完看代码
public boolean isSymmetry(TreeNode left ,TreeNode right){
if( left == null && right == null){
return true;
}
if( left == null || right == null){
return false;
}
if(left.val != right.val){
return false;
}
boolean isleft = isSymmetry(left.left,right.right);
boolean isright = isSymmetry(left.right,right.left);
return isleft && isright;
}
public boolean isSymmetric(TreeNode root) {
if(root == null ){
return true;
}
if(root.left == null && root.right == null){
return true;
}
if(root.left == null || root.right == null ){
return false;
}
boolean i = isSymmetry(root.left ,root.right);
return i;
}
现在是不是思维就开始活跃起来了,现在开始上强度。
第五题
给定⼀个⼆叉树,找到该树中两个指定节点的最近公共祖先236. 二叉树的最近公共祖先 - 力扣(LeetCode)这个我们看题目感觉对这个题目不是很可以理解,所以我们看详情

怎么说,其实就是两个节点往上找,找到最近的公共节点,但是公共节点也可以是两个节点的其中一个,我们理解了题目,就可以来想一想我们这到题的思路了,因为这个要往上找,但是我们的二叉树是不存在向上查询的功能,所以我们这个一定要使用递归,从这个节点一直往下递归一直到找到这两个值,我们就来想一想,会有这样递归会有什么可能呢,一,两个值都在左子树,而,两个值都在右子树,三,一个左,一个右,四,还有没有可能一个值就是这个节点呢。一个值随机在左右子树。现在我们就来对这些情况进行分析和处理,
一,都在左子树或右子树,你好好想想,都在一边,那这个节点还是最近的公共节点吗,肯定不是啊,我举一个例子
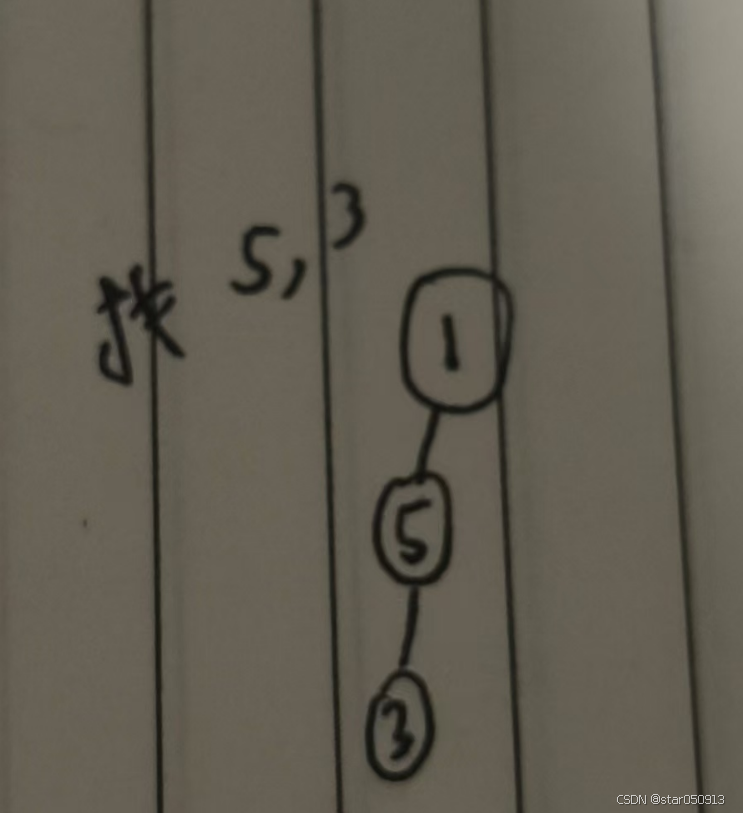
我们可不可以认为5才是最近公共节点(就是情况四),所以说这种情况其实是不成立的。
二,一个左,一个右,这种情况是不是刚刚好就是最近公共节点,但凡他上一个节点,就在同一边了,他往下一个节点,就有一个找不到,
三,一个是自己还有一个在左或右子树,这种情况也是刚刚好,上一个下一个都不行,所以我们就只需要考虑二,三就可以了
所以,那值出现的情况只有三种(后面讲三种都是这三种),一、左子树,二、右子树,三、根节点。而实现最近公共节点的条件就是两个值同时出现,但是一定要是三种情况种的两种(但是不能同时出现在一种情况),所以我们就可以设定找到了就返回1,三种情况加起来就刚刚好是2。也只有是2才是对的,别的取值都是错的。我们就返回这个加起来是2的节点就可以了(但是因为方法返回值已经是int了,所以我们就可以定义一个类变量,来保存返回的节点)思路讲完了,看代码实现
class Solution {
private TreeNode ice = null;//这个就是返回的节点
public int foundata(TreeNode root ,TreeNode p ,TreeNode q){
if(root == null){
return 0;
}
int isself = 0;
if(root.val == p.val || root.val == q.val){
isself = 1;
}
int isleft = foundata(root.left,p,q);
int isright = foundata(root.right ,p,q);
int count = isleft + isright + isself;
if(count == 2){
ice = root;
}
return count>0? 1:0;
}
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
ice = null;
if(root == null){
return null;
}
int i = foundata(root,p,q);
return ice;
}
}有没有感觉要张脑子了啊,我们继续
第六题
根据⼀棵树的前序遍历与中序遍历构造⼆叉树105. 从前序与中序遍历序列构造二叉树 - 力扣(LeetCode)
上一张我们埋下了这个伏笔,现在开始写吧,我们还是老规矩,想思路,我们先想前序遍历是什么样的,嗯~~,根左右,中序呢,嗯~~,左根右,也就是说前序的第一个节点就是根节点,而我们拿到了根节点之后,就可以在中序里面知道,根左边的是左子树,右边的是右子树,我们就可以使用这个方法一直递归下去,直到什么时候停呢,想一想,傲,只有一个元素的时候停。所以我们就可以先写代码了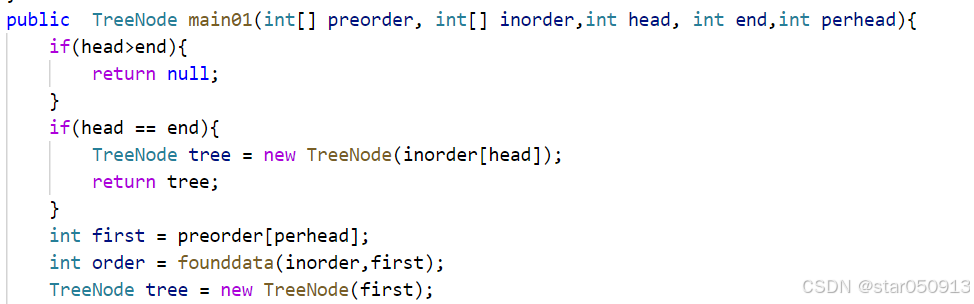
我们先来理解一下啊,这个head>end就是我传一个数组,结果数组就没有元素,所以就返回空,而head == end就是只有一个元素,那我们是不是直接创建这个节点返回就行了,理解了,好,我们接着往下写,我们已经拿到根节点了,并且知道了根节点的位子,接下来就是递归中序的左子树,右子树了,所以我们要传参了,首先两个数组(前序和中序)是一定要传的,接下来就是head和end对于中序的左子树来说,head就是这个数组的head,而end就是根节点的前面一位所以就是inorder-1,而perhead(这个是前序的头节点,因为在前序中我们只需要头节点来确定根节点是哪个,前序除此之外没有任何用处,所以我们可以就传perhead)就是当前的perhead+1(为什么,因为前序是根左右,所以根的下一个元素就是左的第一个元素,也就是左边的根节点)这个是对于中序的左子树,现在我们来谈论中序的右子树,一样的head和end,head自然就是inorder+1(中序中根的下一个节点嘛)而end就是这个数组的末尾了,重点来了,就是右子树的perhead怎么计算啊,在前序遍历中我们知道前序是根左右,所以右子树的第一个元素就是原perhead(根)+左子树的个数(这个不就是尾-首不要忘记还有+1噢)再加1就对了。思路都理清楚了,就看代码吧。
public int founddata(int[] inorder ,int first){
for(int i = 0;i<inorder.length;i++){
if(inorder[i] == first){
return i;
}
}
return -1;
}
public TreeNode main01(int[] preorder, int[] inorder,int head, int end,int perhead){
if(head>end){
return null;
}
if(head == end){
TreeNode tree = new TreeNode(inorder[head]);
return tree;
}
int first = preorder[perhead];
int order = founddata(inorder,first);
TreeNode tree = new TreeNode(first);
tree.left = main01(preorder,inorder,head,order-1,perhead+1);
tree.right = main01(preorder,inorder,order+1,end,perhead+order-head+1);
return tree;
}
public TreeNode buildTree(int[] preorder, int[] inorder) {
if(preorder.length == 0 || inorder.length == 0){
return null;
}
TreeNode root = main01(preorder,inorder,0,inorder.length-1,0);
return root;
}
第七题
⼆叉树中序非递归遍历实现94. 二叉树的中序遍历 - 力扣(LeetCode)
其实这个题再上一篇我们也埋了伏笔,就是递归的操作可以实现先进后出的操作,而我们的栈也刚好可以满足先进后出的操作,所以我们使用递归实现的操作,栈应该也是可以实现的,而二叉树的遍历有前序中序和后序,我为什么要选择中序呢,因为前序太简单了,后序和中序有共通之处,所以我选择中序,因为中序是左根右,所以我们要先一直向左走,因此我们先写一个循环,一边找一边把题目入栈一直找到了左子树为空的节点,我们再看这个节点有没有右子树,如果有,嗨,就先把栈顶出栈再继续往左找,一边找一边入栈,一直循环下去,直到,右子树也为空了(不容易啊)我们就可以再次出栈了,再找栈顶的元素有没有右子树,有就继续,一直到全部元素都出栈,栈为空了,我的任务完成了

所以来看代码
public List<Integer> inorderTraversal(TreeNode root) {
Stack<TreeNode> stack = new Stack();
List<Integer> list = new ArrayList<>(20);
if(root == null){
return list;
}
TreeNode cur = root;
while(true){
while(cur != null){
stack.push(cur);
cur = cur.left;
}
if(stack.empty()){
break;
}
TreeNode middata = stack.pop();
list.add(middata.val);
cur = middata.right;
}
return list;
}
兄弟们,怎么样啊,今天就先到这吧,下次见




















 977
977

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








