自适应信号分析框架

基于自主服务组件的自适应信号分析软件框架

1 引言

随着大量传感器部署在复杂环境中，涌现出了海量需要被感知、采集、存储和分析的数据/模拟信号。环境变化测量失真会导致采集到的信号特性发生变化。这些信号特性会影响对信号进行推断的性能。为了达到期望的性能指标，需要在分析前对信号进行调理。这要求使用算法组合来实施适当的预处理策略。通常，领域专家要找到合适的分析组合来调理信号是十分繁琐的。他们需要花费大量时间对大量的训练信号数据库进行实验，并基于模板开发模型，以帮助对测试数据进行推断。同样，数据分析专家在不考虑基于领域知识的分析和设计约束的情况下，也很难收敛到合适的组合。

有必要开发一种计算工具，以帮助领域专家和数据分析专家协作，形成初始的算法组合。该工具还应支持系统化的优化策略，以实现功能与性能需求之间的平衡。该工具应基于一种能够适应环境和上下文的软件架构框架。该软件框架应支持对数据的动态监控，以及在系统、推断性能、数据和环境约束下进行算法调度与执行的机制。所需框架需要整合有关数据模型、相关质量指标监测以及计算模型的领域知识。当信号质量指标被量化后，可辅助决策，收敛到合适的算法组合，以提升预处理阶段的质量。信号质量沿多个质量维度进行评估，如准确性、一致性、有效性、密度和完整性。基于定义为这些测量质量维度子集函数的效用指标，可对用于信号预处理并改善特定维度质量的算法组合做出决策。信号处理应用的计算模型可以用数据流图 [13] 来定义。图中的节点是执行算法的计算单元，边表示交互结构，反映计算单元之间的数据依赖关系。当计算单元在其连接的边上接收到数据时即被激活，从而实现数据驱动的执行。为了满足执行过程中的适应性需求，在处理测试数据时，我们需要一种自适应计算模型，能够调整其相互作用的算法组合及其参数。数据流图以最少的系统级实现细节来表示应用功能。数据流图可根据不同的应用场景进行重新配置。数据流计算模型使设计者能够系统化地制定应用程序设计的设计流程，并将系统、领域和软件约束集成到这些设计流程中 [4, 17]。

从执行角度来看，基于数据流的计算模型最好使用基于参与者/代理的框架来实现，其中每个代理都是一个节点，并且能够适应其功能（连接性和操作设置）。为此，我们提出了一种面向服务的软件组件框架。服务组件充当代理，为整体推断提供服务（算法的执行）。它们需要根据决策指标以正确的配置进行组合。我们已确定服务组件集成语言（SCEL）[15]适用于数据流图的设计与执行，能够根据用户需求和变化的环境条件调整其计算单元和连接结构。服务组件集成是一组以数据流图结构组织的服务组件。集成中的每个组件都可以基于内部定义的过程、知识和操作策略执行。SCEL 是一种定义编程语言抽象的语言，允许表示知识元组、根据策略定义行为和聚合，并实现服务组件 [15] 之间的交互、适应性和上下文感知。

基于组件的软件环境为提高动态环境中的性能提供了灵活性和适应性。应用程序可以使用组件进行建模，以组合出最佳性能，并在执行期间动态重新配置 [2]。自治组件和组件集合是一种将应用程序建模为数据流图的方法，其中包含可相互交互和适应的独立且分布式的计算单元。已定义了用于编程自治组件演化和交互的编程语言抽象 [19]，这有助于服务组件的组合。

2 服务组件集成语言（SCEL）

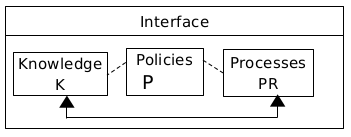
编程语言抽象有助于通过行为、知识、聚合模型和策略来描述自治组件[19]。行为描述了计算的进展方式，并作为算法执行。知识库存储提供高级原语（元数据），用于管理来自不同来源（环境、其他组件）的信息。每个知识库都具备添加、检索和撤销知识项的操作。聚合定义了不同组件如何组合形成一个整体。组件接口中公开的属性支持组件间的组合与交互。策略用于控制并调整各个组件的动作，以完成特定任务。这些策略基于信号质量指标的领域规则以及影响质量指标的算法可重构参数。如图1所示，组件的实现基于：

a) 一个接口 I，以属性的形式发布并提供有关该组件的信息。
b) 一个知识库 K，它是一个 N 元组，包含知识元素。可以通过用户定义的元数据类型进行引用。
c) 一组策略 P，用于规范不同组件之间的交互。这些策略可能是交互策略或服务级别协议。它们还指导过程与知识库之间的交互。
d) 一个过程 PR，激活时可执行本地计算（数据驱动）。该过程还可以协调与知识库的交互，或执行适应和重新配置。

2.1 SCEL的运行时环境

jRESP 是一个 Java 运行时环境，提供了一个用于开发自治组件 [3] 的框架。jRESP 提供了一个 API，允许使用 SCEL 语言结构来控制自治组件的计算和交互。一个 SCEL 程序由一组组件构成，每个组件都拥有自己的知识库。这些组件在动态环境中协同工作以实现给定目标。SCEL 组件通过类 Node 实现。一个节点包含一个知识库、一组进程和一组策略。关于节点的结构和行为信息被集中在一个接口中。节点通过支持点对点和面向组通信的端口进行交互。SCEL 进程通过抽象类 Agent 作为线程实现，该抽象类提供了实现 SCEL 动作的方法。策略可用于指导本地操作以及调节组件之间的交互。

2.2 服务组合适应

针对数据流模型设计结构适应策略有多种方法。这些方法需要一种用于适应和在数据流模型之间进行选择的度量。这些度量可以基于模型、规则/策略、目标或效用。在基于模型的方法中，模型表示实际状态和期望状态，包括数据模型或环境模型。通过分析模型，可以定义合适的适应规划器。在基于规则的方法中，规则确定分析框架的功能和操作策略。规则在设计时定义，依赖于领域知识，并对算法组合的设计空间施加约束。基于目标的方法旨在实现特定的推理目标。目标影响系统应如何重新配置和执行。在设计时，适应规划器必须定义实现这些目标的规划。在基于效用的方法中，在各种方法中，效用是根据用户为实现目标所获得的信息价值来定义的。其目标是最大化实现特定目标的整体效用。

在信号处理应用中，模型包括数据模型（统计的、频谱的或拓扑的）以及基于数据流的计算模型（适当配置和调度的算法组合）。规则是对模型参数的约束，以及对质量和服务性能指标的上下限。目标包括参数估计、事件/假设检测、多维测量聚类，以及将测试测量分类到一组预定义假设中的某一类。针对每个目标，可以定义一个数值性能指标，用于量化目标的实现程度。信号预处理的一个关键方法是沿准确性、一致性、有效性、完整性和密度等维度定义质量指标[18]。然后可基于这些维度的数值度量计算出效用。该效用度量在测试信号上的取值可用于决策应采用何种计算模型，通过改进选定的若干质量指标，以提升面向目标的效用。对于每个质量指标，都存在能够改进它（提高或降低）的算法。这些算法由各个服务组件执行。组件所提供的改进程度是其服务质量（QoS）的度量。

需要一个代理中介来与服务组件进行协商，以针对特定目标和期望性能选择最优的组件。下一节将描述一个形式化框架。

3 基于服务质量的服务组件组合

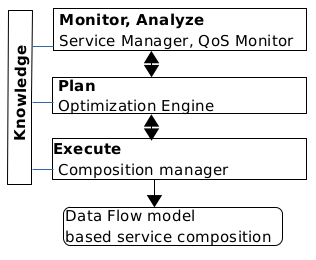
基于数据流的计算模型的设计需要一个决策度量，可用于组合服务组件。这可以通过为每个组件指定服务质量度量来实现，从而有助于选择最合适的组件来解决问题[16]。服务质量感知应用由可动态选择的服务提供者（SP）组件和一个服务质量代理（QB）组成，该代理可代表各个SP组件进行协商，以满足服务质量保证[11, 14]。基于模型的面向服务系统自适应（MOSES）是一个用于以服务质量驱动的服务系统运行时自适应的框架[5]。MOSES作为服务代理，能够在环境/信号变化时提供组合服务和自适应能力，以满足不同服务类别的服务质量目标。MOSES基于自主计算中的IBM监控‐分析‐规划‐执行分层模型[6]。该分层模型以及各元素与知识库之间的交互框架如图2所示。监控/分析组件负责监控质量指标，并协助规划组件组合一组服务组件并执行数据流模型。规划层中的优化引擎根据与服务提供者协商的服务级别协议（SLAs）求解优化问题，以实现最优组合。服务组件以及潜在的组合模型集合由监控和分析组件维护更新，这些组件与领域知识数据库进行接口。

4 使用SCEL框架对模拟信号进行预处理

在确定了用于选择计算模型的形式化框架后，我们现在定义质量指标，以帮助选择和执行用于调理模拟信号的算法组合。预处理是在实际分析过程开始之前为调理信号/数据而采取的一系列操作。它是从原始数据到新数据集的转换，使得新数据保留有价值的信息，包括有效性、新颖性、有用性和可理解性[9]。

为了实现有意义的预处理，领域专家和数据科学家需要共同协作，验证并确认特定预处理技术的使用。预处理也是迭代的：某些预处理技术需要经过多次迭代使用，直到获得最佳的信号分析结果。为应对这些挑战，我们提出采用基于服务组件的软件架构，利用SCEL提供的工具来设计组件集合。集合中的组件可以以数据驱动的方式相互交互。组件间的交互能够实现适当地调理数据/信号的目标，从而以期望的性能做出相关推断。基于SCEL的动态服务组合支持在动态环境和数据密集型应用中，采用数据驱动的框架来决定所使用的计算模型。

根据有关信号的先验信息、基于领域的质量指标规则以及用户指定目标，我们提出开发一种软件框架，该框架能够观测测试数据、评估质量指标，并生成组件集合以执行最适合的信号预处理算法组合。组件集合中的调度或控制流取决于信号特性和信号分析目标。我们的方法基于MOSES架构，在该架构中我们定义了

表1: 质量维度

数据质量	量化质量的数值指标
准确性	信号动态模型的本征模态
一致性	统计、频谱和拓扑结构
有效性	T‐F 平面上的能量分布
密度	信号采样率的测量
完整性	信号中缺失样本的比例

监控、分析、规划器、执行的主要组件，使用SCEL，具有以下功能：

a) 监控组件 ：该组件监控信号并计算与预处理和进一步分析决策相关的质量属性。它调用信号处理工具箱中的一组函数来计算质量指标向量。它可以访问知识库，以指导计算指标时的参数选择。在运行时，该组件可被规划组件查询，由规划器决定用于提升质量指标的最优算法组合。模拟信号在准确性、一致性、有效性、密度和完整性这些质量维度上的对应关系如表1所示。来自不同应用领域的信号在评估质量指标时将需要不同的参数集。此类领域知识可以作为知识元组编码到监控 SCEL组件中，用于学习模型和质量指标评估。

b) 规划组件 ：该组件向监控组件查询质量指标，并将其存储在本地知识库中。然后，对这些指标应用基于领域的规则（边界/分布），以评估效用，并决定需要改进的质量指标以及相应的算法组合。

c) 执行 ：该组件能够实现服务组件组合，并定义它们之间的交互规则，从而改善已识别的质量指标。它向相关组件发送消息以定义其交互策略，进而确定组件之间的数据流。随后，在组件集合中为选定的组件触发执行，采用适当的控制流和数据流模式。

d) 计算单元 ：这些组件是独立的服务组件，用于学习模型或使用算法执行定义的计算。它们的交互以数据流图的形式进行组织。这些组件通过与执行组件接口来获取其重构策略。

e) 数据存储组件 ：该组件存储用于学习模型的模板信号以及来自测量/传感器的原始测试信号的链接。监控、规划器和执行组件可以查询此数据组件以执行各自的操作。提出的架构如图3所示。

需要注意的一个关键点是，如图3所示的架构中，与 MOSES方法中的分层层次结构方法不同，数据、监控、规划器和执行组件之间形成了一个闭环。计算单元从数据中学习到的模型可以通过监控组件提供的信息进行优化/重构，这些信息提供了与信号预处理相关的度量。这些重构的数据模型

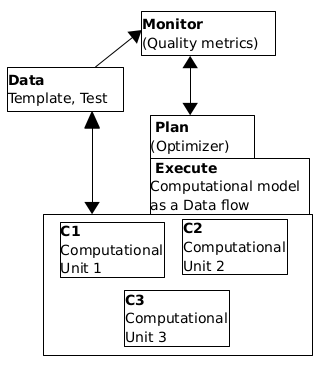
可以进而指导正确数据的选择，从而改进质量指标，反过来有助于迭代地重构计算模型，以更高性能实现目标。服务组件的选择基于组件C1、C2、C3与规划器/执行组件之间预先定义的服务水平协议。

5 数值示例

信号/数据的分析遵循过程‐结构‐属性‐性能模型。一个过程（算法）在信号上引出一种结构（动态的、统计的、频谱的、拓扑的），从而产生某种属性（准确性、一致性、有效性、完整性、密度）以及在估计、检测、聚类、分类等目标上的性能。此处的属性即为我们所指的表1中的质量指标集合。信号中的结构可以通过统计、频谱和拓扑一致性的数值指标进行量化。一旦评估了这些指标，便可用于决策服务组件的组合，以提高整体效用，使信号处于良好条件，并更有利于实现用户指定目标。我们以信号的动态结构为基础，给出单一质量指标（准确性）的一个示例。该指标作为决策指标，用于衡量测试信号在测量信号存在噪声和异常的情况下对期望模板信号的逼近程度。文中还强调了为提升该指标而对应的服务组件选择方案。

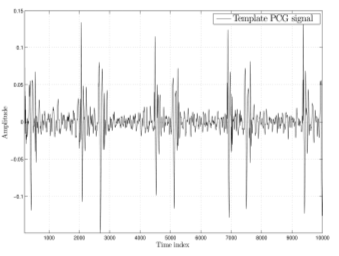
我们以心音图（PCG）波形作为一个用例（图4）。需要对该信号进行临床推断，以检测异常，辅助诊断心脏病。给定一个测试信号，一个关键目标是在不扭曲测量信号中基本的临床相关结构（统计/频谱/拓扑）的前提下，执行去噪/异常减少。第一步是对信号进行质量检查，以便采取正确的处理方法。原始噪声信号可被视为一种随机过程。该随机过程可看作是一个动态系统的输出。描述该动态特性的模型通常是非线性的：

$$
\frac{dx}{dt} = f(x, t, \mu)
\quad (1)
$$

其中 $ x(t) $ 是与时间相关的状态空间，$ \mu $ 是系统参数。当系统动态模型未知时，通过采集信号的数据测量值作为状态空间，并利用这些数据来近似系统的动态特性。动态模态分解（DMD）通过对随机过程的非线性模型（如式 (1) 所示）构建一个线性近似，表示为 [12]：

$$
\frac{dx}{dt} = \hat{A} \cdot x
\quad (2)
$$

通过对多个信号的实验评估，我们观察到，通常情况下，该比率：

$$
C = \frac{\sum \text{dominant eigenvalues}}{\sum \text{minor eigenvalues}}
\quad (3)
$$

由状态转移矩阵 $ \hat{A} $ 计算得出，是信号状态（噪声/失真）的指示。图5显示了状态转移矩阵的本征模态图。观察到两个主要的本征模态，对应于图4所示心音图波形中具有临床意义的两个主要波形段。

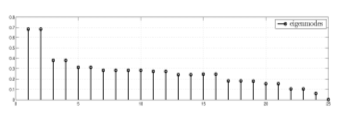
信号状态指标对准确性质量指标进行数值量化，用于确定去噪或异常减少的策略。如果信号状态指标较低，则可能存在严重的异常/离群值，或者加性噪声已经干扰了信号的整体时间演化，此时需要在全局层面进行条件处理。如果条件指标较高，则表明加性噪声的方差较小，适合在局部层面（小的时间变化）进行条件处理。从图6可以看出，在一组100个无噪声/失真/异常的训练信号上，信号状况 $ C $（归一化）的分布范围为 (0.25, 1)。对于测试信号，若条件数低于0.25，则表明需要进行去噪或异常去除。

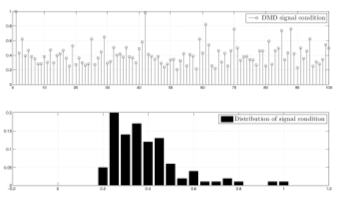
在全局层面实现信号调理的过程中，我们首先为原始测试信号学习一个数据模型，以捕捉其基本的统计与频谱结构。然后，基于期望信号的先验知识对其拓扑（图）结构对该数据模型进行重构。利用重构后的数据模型来重建调理后的信号。一种用于信号分析与合成的信号子空间（数据模型）学习的数据驱动方法是K‐SVD算法[1]。K‐SVD方法求解如下优化问题：

$$
D_c, X_c = \arg\min_{D,X} |Y - DX|_F^2 + \lambda|X|_F^2
\quad (4)
$$

这里 $ D \in \mathbb{R}^{n \times p} $ 和 $ X \in \mathbb{R}^{p \times k} $，$ |X|_F $ 表示矩阵的弗罗贝尼乌斯范数。$ Y \in \mathbb{R}^{n \times k} $ 是每组为 $ n $ 维的 $ k $ 个测量值的集合。$ X $ 是估计的合成系数矩阵。基于这些合成系数的加权线性组合可重建信号。为了获得一个具有特定结构的信号，我们需要对数据模型施加结构约束。为此，我们首先在模板信号上学习一种拓扑结构。设无失真/无噪声训练信号 $ Y_d \in \mathbb{R}^{n \times p} $ 的多个测量值通过图拉普拉斯矩阵 $ L \in \mathbb{R}^{p \times p} $ 表征其拓扑结构。该图包含 $ p $ 个节点，每个节点上有 $ n $ 个测量值。该拉普拉斯矩阵是半正定的（对称且具有非零特征值），可通过求解[8]得到：

$$
L_d = \arg\min_L \text{trace}(Y_d L Y_d^T) + \lambda |L \cdot \mathbf{1} - \mathbf{0}|_F^2
\quad (5)
$$

受 $ L = L^T $ 约束，其中 $ \mathbf{1} \in \mathbb{R}^{p \times 1} $ 是单位元素列向量，而 $ \mathbf{0} \in \mathbb{R}^{p \times 1} $ 是全零列向量。注意 $ L_d = D_G - A $，其中图邻接矩阵为 $ A $，度矩阵为 $ D_G $。度矩阵是一个对角矩阵，其每个对角线元素等于图邻接矩阵 $ A $ 中与各节点相关联的加权边之和。我们对 $ L_d $ 进行归一化，使得 $ D_G $ 成为单位对角矩阵。需要注意的是，该图捕获了信号的全局结构，将此全局结构施加于数据模型（字典）有助于重构出主要异常/噪声被抑制的信号。为此，我们在信号模型 $ D_C $ 上施加图结构约束，并重新估计其近似值：

$$
D_S = \arg\min_D |D_c - D|_F^2 + \lambda_1 \cdot \text{trace}(D L_d D^T)
\quad (6)
$$

注意，(6) 中的重构是一种模型校准形式。基于图模型的校准可得到能够以期望的拓扑结构重构信号的合成系数。字典原子的线性组合重构出保留基本的统计、谱和拓扑结构的期望信号。利用新的图结构字典，我们估计相应的系数：

$$
X_S = \arg\min_X |Y - D_S X|_F^2 + \lambda_2 |X|_F^2
\quad (7)
$$

由 $ Y_S = D_S X_S $ 给出的重构信号具有降低的噪声和异常值/离群值。对于局部层面的条件处理（平滑小的时间变化），我们通过求解对合成系数施加图约束：

$$
X_{S1} = \arg\min_X |Y - D_S X|_F^2 + \lambda_3 \cdot \text{trace}(X^T L X)
\quad (8)
$$

在所有问题 (5,6,7,8) 中，拉格朗日惩罚的选择决定了字典结构和合成系数的约束。在 (8) 中的合成系数估计受到约束，使得放置在图的每个 $ k $ 个节点上的 $ p $ 个系数的每一行，根据编码在 $ L $ 中的边连接性，与相邻连接节点上的 $ k $ 个系数相关联。由 $ Y_{S1} = D_S X_{S1} $ 给出的重构信号的小的时间变化被平滑，且测试信号的主要临床相关波形段被保留。

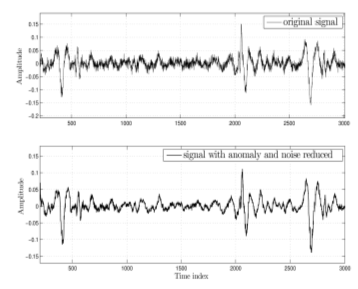
如图7所示，使用图结构字典和合成系数重构信号时，不仅保留了原始信号的基本全局结构（波形幅度、时间缩放和周期性），还平滑了由加性噪声引起的局部变化。信号状态指标从0.3提升至0.5。

模型的选择（字典、图）取决于在测试信号上评估的质量指标。(4)中的字典模型和(5)中的图模型由两个服务组件学习得到。然后，规划组件根据从(3)计算的信号状态质量指标触发这些组件的适当组合。根据质量指标的允许范围，两种可选的计算模型对应于：
a) 求解公式(6)中的字典和系数，其中字典被校准具有用于全局调节的图结构，以及
b) 求解(8)中的字典系数，其中系数通过用于局部调节的图结构进行校准。

计算组件会持续查询监控、规划器和执行组件，以了解所需变更，从而能够重新配置其数据流。字典和图学习组件可以通过SCEL结构中的适当策略进行配置，以周期性地重新学习数据和拓扑模型。这是为了确保这些模型能够反映被监控和处理信号的真实状态。该模型更新的触发条件基于被监控信号的拓扑一致性度量，该度量可通过将测量信号投影到先验图结构上来计算，即：

$$
T = \text{trace}(Y_d L Y_d^T)
\quad (9)
$$

如果检验统计量 $ T $ 超出了领域相关阈值，则将学习一个新的图结构和字典，用于对未来的测试信号进行条件化。测试信号的图拓扑结构的任何变化都将导致边连接性发生变化，并改变在 (9) 中计算的投影值，从而触发学习新的图模型并重新求解 (6,7,8) 以获得新的结构化信号。

基于统计和频谱特性，可评估其他用于检测信号结构变化的度量，如表1所示。请注意，Graph服务组件具有双重作用：既有助于模型校准，又可作为触发器指示测试信号中是否存在拓扑变化（来自(9)）。规划组件根据对信号状态的测量来调用这两种角色之一。监控组件使用在(9)中定义的检验统计量来触发模型更新，并通知规划组件使用更新的数据和结构模型来规划计算模型。这种在数据、监控、规划和执行服务组件之间用于运行时重构的反馈机制，通过SCEL中定义的自主服务组件得到了良好支持。

6 代码细节

SCEL进程通过抽象类Agent作为线程实现，该抽象类提供了实现SCEL动作的方法。节点声明如下：

节点 node0 = new 节点("node0", new TupleSpace());

声明并添加一个端口到该节点：

public static 虚拟端口 vp1 = new 虚拟端口(10);
node0.addPort(vp1);

每个组件（节点）都连接到一个代理以描述其操作或行为。例如，我们定义了一个新代理，该代理调用字典学习算法。此代理连接到一个节点（一个字典服务组件）：

代理 a1 = new 字典(s);
node0.addAgent(a1);

该节点可以查询并响应来自其他组件的信息。查询通过元数据定义进行，可访问其他组件本地知识库中相应的元数据。组件的本地知识库通过元数据“DC”进行填充：

put(new Tuple(("DC"), s), Self.SELF);

元数据DC可以表示学习到的字典。独立组件立即开始执行，并将其计算的值放入自身的元组空间中。依赖组件需要获取数值，因此会暂停执行，直到其发出的查询得到响应为止。已使用Eclipse IDE基于SCEL完成了该服务框架的基本实现，并验证了信号去噪/异常减少的结果。

7 结论

所描述的用于信号预处理的服务组件集合框架通常适用于在多个领域和复杂环境中生成的模拟信号。质量维度可以被量化，并用于在不确定性条件下，针对最适合对数据进行推断的算法组合做出决策。与传统分析平台相比，该框架的一个关键优势在于其适应性，能够根据外部环境、基于领域的规则以及应用需求进行调整，有助于对数据做出正确的推断，同时减少测试结果验证与确认以及模型重构所需的人工工作量。服务组件的 jRESP 运行时环境能够利用 Matlab、R 或 Julia 等科学计算语言编写的工具箱来执行算法。每个组件都可以调用不同信号处理库中的算法，避免了单一语言的限制。当前的规划组件实现使用预定义阈值和数值质量指标上的规则来做出决策。我们需要开发形式化方法来指定和验证服务组件之间的QoS要求或服务水平协议，以便自动化基于数据流图的服务组件组合所需的推理过程。

此外，规划组件必须具备上下文感知能力，以便控制服务组件组合中的变更范围。需要开发面向上下文的编程语言构造，用于创建能够随时间变化和演化的组件集合，并支持多种操作上下文[10]。目前正在进行的工作旨在为信号处理中的每个目标形式化定义效用，该效用是数值质量指标的函数，并在字典和图模型针对噪声与异常减少、缺失值填补及降维等预处理操作进行重构时，识别效用变化的模式。

8 更广泛的影响

复杂系统的工程设计需要在计算复杂性、能量、存储和通信带宽等系统约束下，对数据进行时间关键决策。形式化的知识表示与推理框架将增强针对复杂系统和过程所产生的信号进行推断的计算模型的设计决策能力。SCEL 方法实现了一种称为动态数据驱动应用系统（DDDAS）[7] 的框架。该框架能够在应用程序运行过程中动态地引入数据，同时也能够通过运行中的应用程序动态地引导测量过程。DDDAS 提高了数据模型的学习能力，并增强了数据分析应用的分析能力。基于服务组件框架实现的数据驱动应用模型（如数据流图），可为能源、制造和医疗保健领域的应用开发统一的计算与测量基础设施。