1.目标
- 地理坐标系的角速度
2.已知量
- 机体坐标系的角速度 gyro_x, gyro_y,gyro_z;
- 欧拉角,pitch,roll,yaw,参考我的上一章节姿态解算知识点1——四元数互补滤波
3.算法总框图
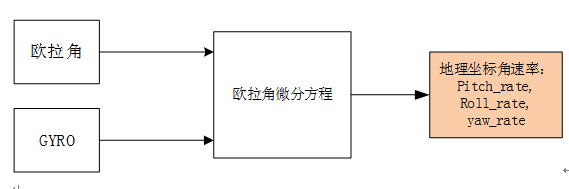
4.数学模型和公式推导
这里坐标系取东北天 --- 右前上
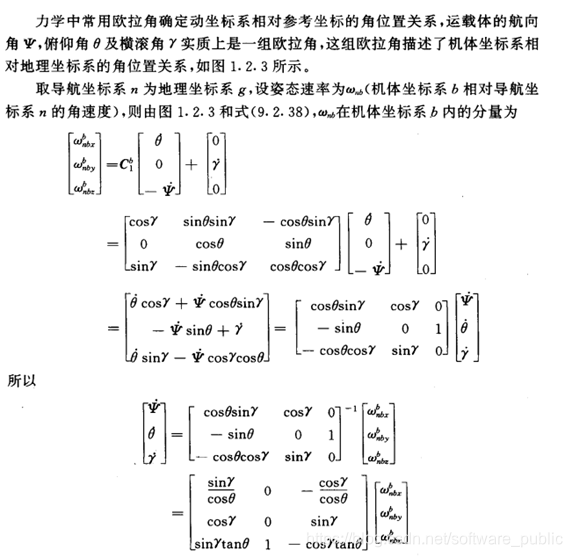
由以上求得地理坐标系的角速度为:
 本文详细介绍如何从机体坐标系的角速度gyro_x,gyro_y,gyro_z及欧拉角pitch,roll,yaw转换到地理坐标系的角速度。通过数学模型和公式推导,提供欧拉角微分方程算法代码,并展示地理坐标系角度速率曲线效果图。
本文详细介绍如何从机体坐标系的角速度gyro_x,gyro_y,gyro_z及欧拉角pitch,roll,yaw转换到地理坐标系的角速度。通过数学模型和公式推导,提供欧拉角微分方程算法代码,并展示地理坐标系角度速率曲线效果图。

这里坐标系取东北天 --- 右前上

由以上求得地理坐标系的角速度为:
 5169
5169
 2万+
2万+
 5657
5657
 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?


