可拉伸生物电子学的力学设计

3 可拉伸生物电子学的力学与设计

3.1 引言

在过去的十年中，可拉伸生物电子学在各个方面都取得了快速的发展和显著的成就，正在重塑这一新兴领域。这类电子器件在保持现有技术功能的同时，展现出传统电子器件无法实现的卓越机械特性，例如像橡皮筋一样拉伸、像绳子一样扭曲、围绕铅笔尖弯曲，且不会产生机械疲劳或工作特性的显著变化[1, 2]。这些优异的机械特性为一系列仿生和生物集成应用[3–11]开辟了道路，而这些应用是其他方法无法实现的。

生物电子学的可拉伸形式通常有两种途径：（1）开发本质上可拉伸的新型材料，用作器件的功能部件；（2）设计新颖的结构，以实现硬质（例如，单壁碳纳米管和石墨烯的模量接近1 TPa[14, 15]）无机功能部件与柔软（例如，某些细胞形态弹性体的模量约为3 kPa[16]，Ecoflex的模量约为60 kPa[17]）弹性体平台的异质集成，从而获得可拉伸的器件系统。本章将重点讨论后一种途径，旨在综述力学引导的设计和模型方面的最新进展。在这种方法中，定量的力学设计发挥着至关重要的作用，其重要性可与传统电子学中的电路设计相媲美[12]。

3.2 波浪、褶皱设计

波浪状、褶皱设计代表了第一种在可拉伸无机电子器件中引入的结构设计。该设计最初被提出，旨在实现单晶硅在橡胶基底上的可拉伸形式，以用于高性能电子器件[18]。这种设计策略的关键在于通过热致膨胀[19]或机械预拉伸[18, 20]，在柔软基底（例如硅胶）中引入初始应变，然后利用该预应变驱动硬质薄膜（例如金属或半导体）形成波浪状、褶皱图案。图3.1a展示了在弹性体基底（例如聚二甲基硅氧烷）上制备波浪状硅带的示意图[18]。图3.1b展示了通过该策略生成的高度周期性波浪状单晶硅带的扫描电子显微照片（SEM）。

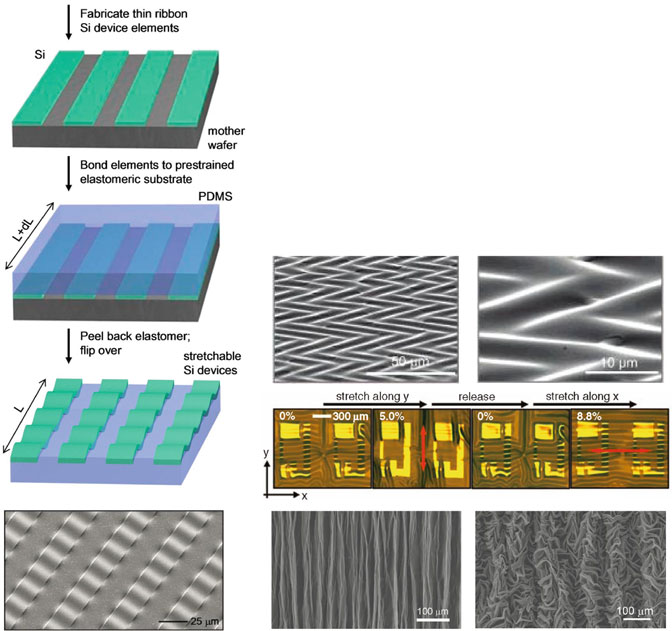
已开发了许多力学模型来预测波浪形带状结构的构型及其可拉伸性。关于这些模型的一些优秀综述论文可在文献[21–23]中找到，因此本文仅介绍其中一些关键结果。在小预应变范围内（例如，0.5 % < εpre < 5%），基于小变形理论提出了能量法以确定屈曲构型[24, 25]。在此方法中，假设屈曲带状结构的面外位移呈正弦轮廓，其波长（k0）和振幅（A0）可通过总应变能最小化来确定。

$$
k_0 = \frac{2\pi h_f}{\left(\frac{E_f}{3E_s}\right)^{1/3}}, \quad A_0 = h_f \sqrt{\frac{\varepsilon_{pre}}{\varepsilon_c} - 1}
$$

其中，下标‘f’和‘s’分别表示带状结构和基底；$E = E / (1 - \nu^2)$ 为平面应变模量，其中 $\nu$ 表示泊松比；$h_f$ 为带状结构的厚度；$\varepsilon_c = \left(\frac{3E_s}{E_f}\right)^{2/3} \cdot \frac{4}{E}$ 为触发屈曲的临界应变，对于PDMS基底上的硅带状结构，该值约为0.034%[18]。

方程（3.1）表明波长与预应变无关（如图‘先前模型’所示），这在较大预应变下（例如 >5%）明显偏离实验测量结果。在此范围内（例如 5 % < εpre < 30%），实验观察显示，随着预应变[26]的增加，波长减小，这主要归因于有限弹性体基底中的变形。为了在屈曲后考虑这种效应，江等人[26]和宋等人[27]建立了解析模型，得到了对屈曲波长和振幅的修正解，即

$$
k = k_0 (1 + \varepsilon_{pre})^{(1 + n)/3}, \quad A = A_0 \frac{\sqrt{1 + \varepsilon_{pre}}}{(1 + n)^{1/3}}
$$

其中，$k_0$ 和 $A_0$ 表示小变形条件下的波长和振幅，$n = 5\varepsilon_{pre}/(1 + \varepsilon_{pre})^{3/2}$。

图3.1c显示，新解[方程（3.2）]能够很好地捕捉应变依赖波长的现象，并且与小变形解相比，对振幅的预测更为准确。该状态下的峰值应变可近似为 $\varepsilon_{peak} \approx 2^{1/3} \varepsilon_{pre} / (1 + \varepsilon_{pre})^{n/3}$；由此可确定避免带状结构断裂的最大预应变。例如，对于断裂应变为~1.8%的硅，其最大预应变为~29%，因此表明波浪形硅带状结构的拉伸性可达~29%。采用类似方法，程等人[28]研究了由非均质双层基底形成的可拉伸带状结构，其中顶部的软层降低了带状结构的峰值应变，从而实现高拉伸性，而底部相对较硬的硬层则为系统提供了鲁棒性和高强度。江等人[29]将上述能量法扩展到三维（3D）模型，并建立了用于研究有限带宽对后屈曲过程中振幅和波长影响的解析模型。

上述力学策略被崔等人[30]和金等人[31]进一步利用，以制备二维（2D）、波浪状电子器件（如图3.1d, e 所示），这些器件在各个方向上均具有优异的拉伸性。在双轴预应变的情况下，屈曲构型的确定相当复杂，如参考文献[24, 25,32, 33]中的计算和理论研究所示。臧等人将这一设计概念引入到弹性体基底上的石墨烯膜中，证明了通过使用极高的预应变（例如高达 400%），可以形成石墨烯膜的脊状或皱褶图案（如图3.1f 所示）。

3.3 岛桥设计

岛桥设计代表了可拉伸生物电子学中广泛使用的另一种通用策略。共面岛桥设计最初由拉科尔等人[35]提出，采用可拉伸的波浪形金属电极来互连有源器件；而非共面岛桥设计则由金等人[36]首次引入，以显著提高拉伸性。

在此设计中，功能元件通常位于岛结构上，而电互连则构成桥结构。在拉伸过程中，刚性岛（具有高有效刚度）几乎保持不变形（例如，应变为<1%），以确保功能材料的力学完整性，而互连部分（具有较低的有效刚度）发生变形以提供拉伸性。因此，桥结构的设计是决定系统有效力学性能（如模量、拉伸性等）的关键。根据桥的几何特性，岛桥设计可进一步分为三类，具体内容在以下小节中详细阐述。

3.3.1 带直线互连的岛桥设计

在这种岛桥设计中，直线互连可以牢固地（通过化学共价键）或弱结合（通过范德华相互作用）到预拉伸弹性体基底上，在预应变释放后形成共面波浪形互连[35]或非共面弧形互连[36]。由于波浪构型已在第 fig. 3.2 节中详细介绍，本小节重点讨论非共面弧形互连，如图3.2a, b 所示。这种设计已被应用于许多可拉伸电子系统中，例如类眼球数码相机[6, 37]和光伏器件[38, 39]。

宋等人[40]建立了一个解析模型来研究带直线互连的岛桥结构的屈曲物理。假设采用正弦表达式来描述后屈曲过程中的弧形轮廓，其中未知振幅通过总应变能最小化确定。通过将互连端部的反作用力和弯矩施加到膜状岛上，也可获得岛上峰值应变的近似解。该模型[40]主要适用于互连的最大挠度（即面外位移）相对于桥长度较小的情况，因为在大挠度范围内，正弦后屈曲构型的假设不够准确。为解决此问题，李等人[41]提出了一种 finite 变形模型，该模型放弃了桥变形的正弦轮廓假设以及岛变形的量纲分析近似。可以得到互连挠度和峰值应变（包括桥和岛上的）的精确解，如图 fig. 3.2c, d 所示。结果表明，采用细长互连更有利于提高拉伸性。

岛桥结构有时会沿偏离互连轴向的方向发生拉伸。在这种情况下，直线互连中可能引发侧向屈曲，这不仅涉及弯曲变形，还包括扭转变形。苏等人[42]建立了可能涉及侧向屈曲等复杂屈曲模式的梁后屈曲理论框架，并采用摄动法获得屈曲互连的振幅。陈等人[43]推导了解析解，用于描述互连在剪切作用下临界侧向屈曲及后屈曲构型。

3.3.2 采用蛇形互连的岛‐桥设计

具有细丝状蛇形结构的互连比直线互连更柔韧，因此即使在弹性体基底中不使用预拉伸的情况下，也有望提供更高的拉伸性。根据目标应用的不同需求，可通过不同的制造工艺使蛇形互连与基底完全键合、部分键合或完全非键合。在不同的键合条件下，蛇形互连的力学行为可能有定性的差异，如下所述。

完全非键合的蛇形互连通常由相对刚性的岛在两端夹紧（图3.3a左侧面板），这些岛完全键合到基底或基底的升高表面浮雕结构上[44]。通过在基底中使用预应变，可以实现蛇形互连的非共面构型[36]，如图3.3a（右侧面板）所示。一般来说，蛇形互连可包含若干个（m个）周期性分布的单元胞，如图3.3b所示，其中代表性单元胞由连接直线的两个半圆组成，具有高度h和间距l。当从两端拉伸时，非键合蛇形互连中可能发生两种不同的变形模式，具体取决于厚度/宽度比(t/w)[44]：（i）非屈曲面内变形，适用于大的t/w（通常相当于或大于1）；（ii）屈曲变形，涉及面内和面外变形，适用于小的t/w（通常小于1/5）。触发蛇形互连中屈曲的临界应变可解析求解[44]，其显示与厚度/宽度比的平方(t²/w²)成正比。

对于拉伸下的非屈曲蛇形互连，张等人[45]基于梁理论获得了弹性可拉伸性的解析解。归一化可拉伸性（图3.3c）随高度/间距比 γ 或单胞数量 m 的增加而增加。基于二维弹性理论，维德伦德等人[46]推导出了非屈曲蛇形结构可拉伸性的另一种解，该解能够提供更准确的预测，特别是对于相对较大的宽度/间距比（w/l）。对于拉伸下的屈曲蛇形互连，张等人[44]提出了一个理论模型，给出了弹性可拉伸性的半解析解。该解与有限元分析（FEA）的结果（图3.3d）吻合良好，表明弹性可拉伸性随蛇形厚度的减小（通过 t/w）或间距的增加（通过 ε_yield·l/w）而增加。相关屈曲构型的解析建模相当具有挑战性，可通过有限元分析（FEA）进行补充[36, 44, 47]。

全键合蛇形互连可与自由站立或预拉伸基底集成，形成两种不同的构型（图3.3e的左上和右上面板）。由于受到基底的约束，全键合蛇形互连的变形模式比非键合情况更为复杂。因此，现有对力学性能的研究主要依赖于计算方法，例如有限元分析[3, 48–54]。张等人[49]研究了关键几何和材料参数对弹性可拉伸性的影响，以及预应变策略带来的增强效果。研究表明，随着金属厚度的增加，弹性可拉伸性显著下降，这主要归因于屈曲模式的变化，如图3.3e（左下和右下图）和图3.3f所示。

3.3.3 岛桥设计与分形启发互连

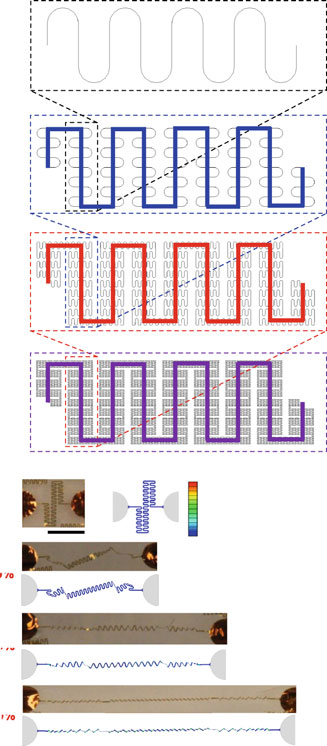
分形启发互连设计最初由徐等人提出[17]，用于实现超可拉伸锂离子电池，并随后在多种其他可拉伸生物电子器件中得到探索[5, 55–57]。通过增加分形阶数，该设计能够充分利用有限空间，在提高功能部件的面覆盖率和系统级拉伸性方面具有显著优势。在此设计中，关键在于设计出能与其他器件组件良好匹配的互连分形布局。图3.4a展示了一种从蛇形结构作为一阶结构开始的分形布局示例。

与蛇形互连类似，分形启发的互连结构（简称为分形互连）也可以以完全键合或完全非键合的方式制备在基底上。在拉伸时，非键合分形互连在 t/w 较大时（通常等于或大于1）发生非屈曲面内变形，在 t/w 较小时（通常小于1/5）发生屈曲变形。对于非屈曲分形矩形和蛇形互连，张等人[45]建立了不同分形阶数下的递推公式，提出了柔性和弹性可拉伸性的解析模型（图3.4b, c）。苏等人[58]提出了一种解析方法，用于确定任意形状分形互连（如锯齿形、正弦形状）的拉伸刚度。对于拉伸下的屈曲分形蛇形互连，力学建模和实验测量中观察到一种有序展开的独特变形机制（如图3.4d所示）[17]。基于这一独特机制，张等人[59]建立了用于分形互连后屈曲分析的分层计算模型（HCM），相比传统有限元分析可显著降低计算量和成本。图3.4e显示了屈曲分形蛇形互连的弹性可拉伸性从一阶时的~10.7%显著增加到四阶时的~2140%。

对于完全键合的分形互连，Fan等人[60]通过结合有限元分析和实验，研究了多种分形布局（例如皮亚诺、希腊十字、希尔伯特等）的变形行为，如图3.5所示。他们还引入了一种高精度方法来测量分形互连的弹塑性转变（或弹性可拉伸性），该方法与有限元分析计算结果具有较好的一致性[60]。由于基底带来的附加载荷，完全键合分形互连的弹性可拉伸性通常远低于完全非键合情况下的对应值。

3.4 折纸/剪纸启发式设计

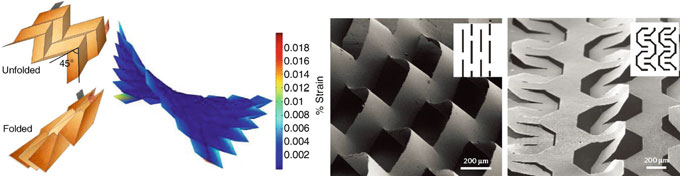
折纸与剪纸代表了一种古老的折叠与切割艺术，通过精心设计的折痕和切割，可以将一张初始的 flat paper 转变为具有不同拓扑结构的目标三维构型。程等人[61]和宋等人[62]最近将折纸设计理念引入可拉伸电池中，以实现高面能量密度和前所未有的可变形性。图3.6a展示了一个三浦折叠的典型示例，其中许多相同的平行四边形面通过‘山折’和‘谷折’折痕连接。在外部载荷作用下，平行四边形面本身通常保持不变形，而折痕区域则发生折叠和/或展开，导致折痕区域应变集中。因此，一项关键任务是降低折痕区域的应变水平，以避免材料断裂或塑性屈服。由于折纸结构复杂的三维几何形状，目前仅对一些有效力学性能（例如弯曲刚度和泊松比）通过解析建模进行了研究[63, 64]，而详细变形和应变分布主要通过有限元分析[65]进行考察，一个示例如图3.6b所示。

kirigami 启发式设计最近被引入可拉伸电子器件中[65–67]。Cho 等人[65]提出了一种分形启发式切割方法，用于具有多壁碳纳米管导电薄膜沉积的较厚硅胶片，可在拉伸下形成非屈曲的旋转单元。该方法实现了一种可拉伸电极，其面积可扩展至>800% 的原始面积。Shyu 等人[66]表明，在薄而刚性的纳米复合材料片上制作的切割网络会引发侧向屈曲（图3.6c, d），并防止局部失效，从而将材料片的极限应变从 4 % 提高到 370 %。宋等人[67]结合折叠与切割技术制造可拉伸的锂离子电池，其可拉伸 >150%。在上述所有情况下，有限元分析都是指导切割布局与几何设计的重要工具。

3.5 结论

本章回顾了为可拉伸电子器件开发的力学引导的设计与模型，涉及三种通用策略。尽管针对每种策略已开发出许多解析与计算模型，但大多数模型基于一定的理想化/假设构建，可能不适用于某些极端条件。因此，未来研究仍面临诸多开放性挑战与机遇。例如，对于键合在柔性弹性体上或被其封装的蛇形与分形互连，建立能够考虑界面脱层的理论模型是十分必要的。对于受折纸/kirigami 概念启发的新兴设计策略，其拓扑优化的褶皱和切割以确定在特定载荷条件下的最佳布局仍是一个尚未开发的研究领域。此外，目前大多数设计主要依赖硅橡胶作为基底材料，尽管其较为柔软，但在许多生物电子应用中，其非线性力学性能与生物组织的匹配度较差[68]。因此，开发用于高质量生物整合的先进基底和/或封装柔性组装平台是另一个值得探索的重要方向。