手写堆排序算法

堆排序算法，是通过堆这种数据结构来实现排序。

堆，其实就是二叉树。由于排序有从小到大、从大到小两种排序方式，对应的堆也分为最小堆和最大堆。

最小堆，就是一颗完全二叉树，每个节点都比其左子节点和右子节点小，整个树的根节点最小。
最大堆，就是一颗完全二叉树，每个节点都比其左子节点和右子节点大，整个树的根节点最大。

用一个连续的数组内存空间，就能表示堆。如下图所示：

 

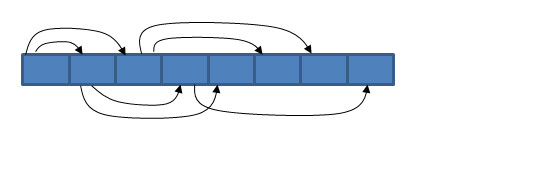
​数组中每个元素，代表最小(大)堆中的一个节点，每个节点最多有两个子节点: 左子节点和右子节点。

上图中的箭头，是从父节点指向子节点，并且位置下标小的子节点为左子节点。
箭头，只是用来描述父子关系的含义，实际代码实现中，并不存在这个箭头，而是用节点在数组中的位置下标，就可以从父节点下标计算出子节点下标，反之，从子节点下标也能计算出父节点下标。

假设父节点位置下标为 idx_parent，左子节点位置下标为 idx_left, 右子节点位置下标为 idx_right：

从父节点下标，计算出子节点下标：
idx_left = idx_parent * 2 + 1;
idx_right = idx_parent * 2 + 2;

从子节点下标，计算出父节点下标：
idx_parent = (idx_left - 1) / 2;
idx_parent = (idx_right - 1) / 2;    // 与 (idx_right - 2) / 2 的值相同

最小堆和最大堆的构建过程，是非常类似的。下面以最小堆为例，说明如何构建一个最小堆。

待排序的元素数量为N。
先分配N个元素的数组空间，用于存储堆数据。初始状态，堆是空的，元素个数为0。<